CONTOURING CONTOUR LINE The line of intersection of

CONTOURING

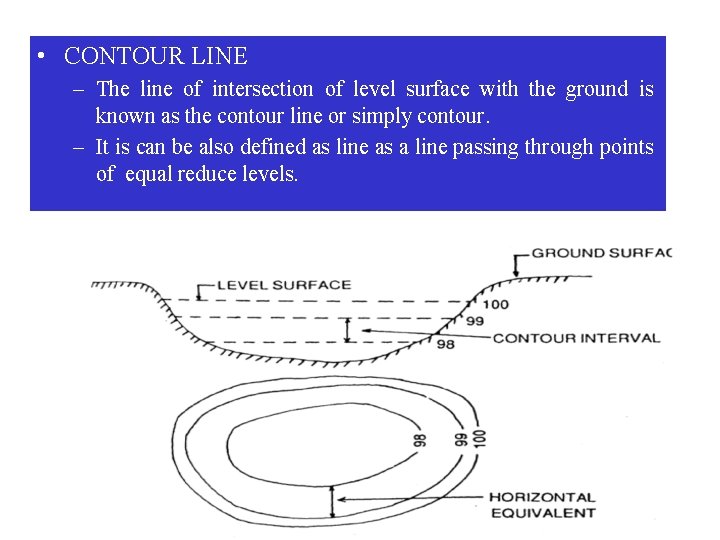
• CONTOUR LINE – The line of intersection of level surface with the ground is known as the contour line or simply contour. – It is can be also defined as line as a line passing through points of equal reduce levels.

• CONTOUR INTERVAL – The vertical distance between any two consecutive contours known as the contour interval – This interval depends on nature of the ground, the scale of the map and the purpose of survey. – The contour interval for flat ground is small and steep for hilly area. • Horizontal Equivalent – The horizontal distance between any two consecutive contours is known as horizontal equivalent. – It varies according to the steepness of the ground

OBJECT OF PREPARING CONTOUR MAP • Nature of the ground surface can not be analyzed form the general map • However for all engineering projects involving roads, railways and so on, a knowledge of the natural of ground surface is required for locating suitable alignments and estimating earth work. • Therefore contour map is essential for all engineering projects.

USES OF CONTOUR MAP • The nature of the ground surface of a country can be understand by studying a contour map • A suitable site or an economical alignment can be selected for any engineering project • The capacity of reservoir or the area of a catchments can be approximately computed • A suitable route for a given gradient can be marked on the map • Quantities of the earth work can be approximately computed.

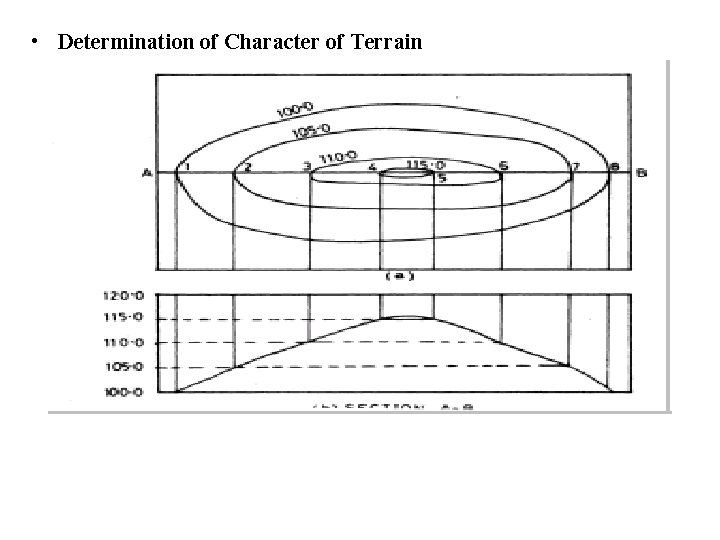
• Determination of Character of Terrain

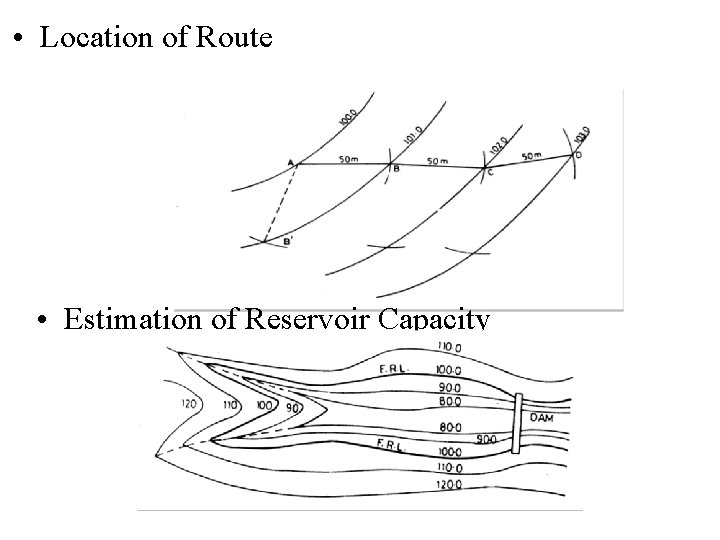
• Location of Route • Estimation of Reservoir Capacity

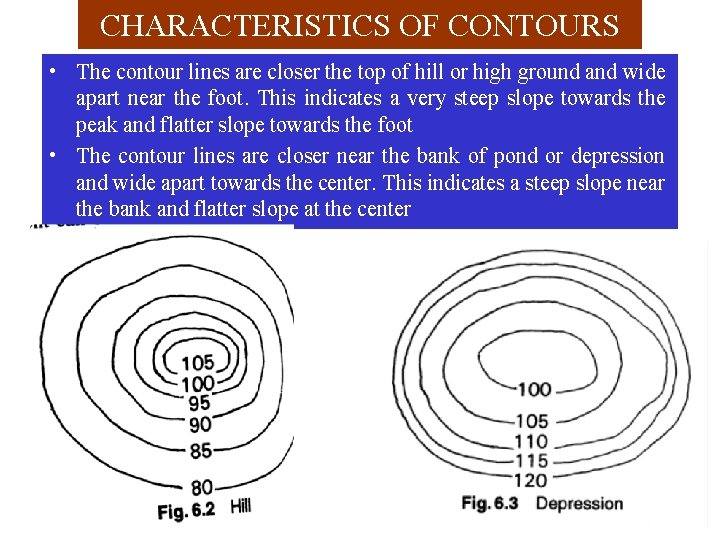
CHARACTERISTICS OF CONTOURS • The contour lines are closer the top of hill or high ground and wide apart near the foot. This indicates a very steep slope towards the peak and flatter slope towards the foot • The contour lines are closer near the bank of pond or depression and wide apart towards the center. This indicates a steep slope near the bank and flatter slope at the center

• Uniformly spaced, contour lines indicate a uniform slope • Contour lines always from a closed circuit. But these lines nay be within or outside the limits of the map • Contour lines cannot cross one another, except in case of an overhanging cliff. But the overlapping portion must be shown by a dotted line.

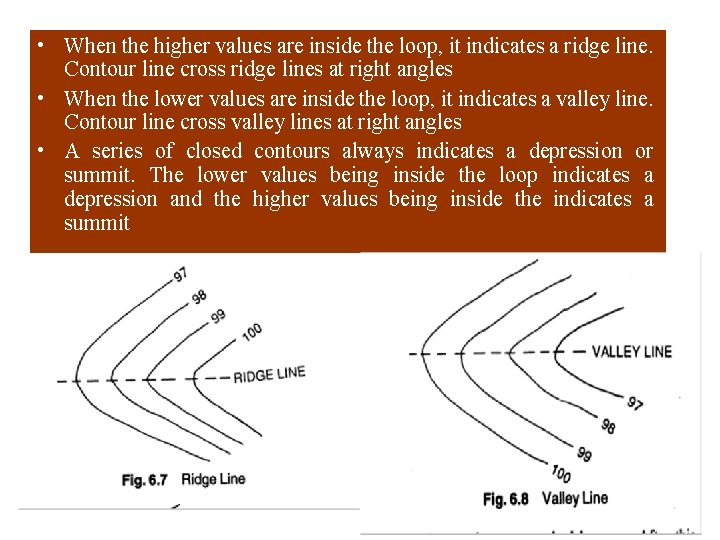
• When the higher values are inside the loop, it indicates a ridge line. Contour line cross ridge lines at right angles • When the lower values are inside the loop, it indicates a valley line. Contour line cross valley lines at right angles • A series of closed contours always indicates a depression or summit. The lower values being inside the loop indicates a depression and the higher values being inside the indicates a summit

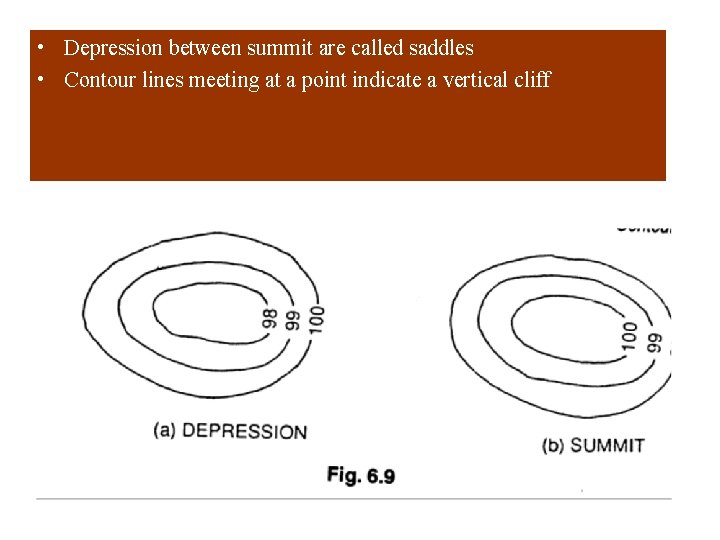
• Depression between summit are called saddles • Contour lines meeting at a point indicate a vertical cliff

METHOD OF INTERPOLATION OF CONTOURS • By arithmetical calculation – Let A & B be two corners of the square. – The RL of A is 98. 75 m & that of B 100. 75 m. The horizontal distance between A & B is 10 m – Horizontal distance between A & B = 10 m – Vertical difference between A & B = 100. 75 – 98. 75 = 2 m – Let a contour of 99. 00 m be required. Then

• Difference of level between A and 99. 00 m contour = 99. 00 – 98. 75 = 0. 25 m – Distance of 99. 00 m contour line from A = 10/2 *0. 25 = 1. 25 m – This is calculated distance is plotted to same scale in which the selection was plotted, to obtain a point of RL of 99. 00 m

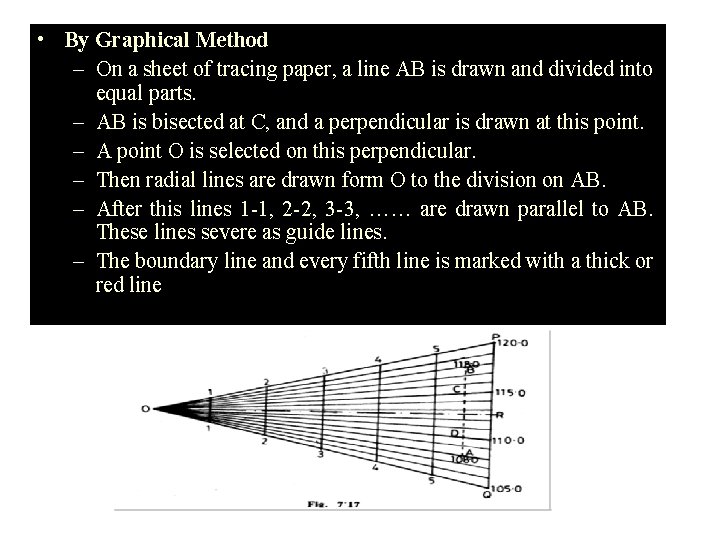
• By Graphical Method – On a sheet of tracing paper, a line AB is drawn and divided into equal parts. – AB is bisected at C, and a perpendicular is drawn at this point. – A point O is selected on this perpendicular. – Then radial lines are drawn form O to the division on AB. – After this lines 1 -1, 2 -2, 3 -3, …… are drawn parallel to AB. These lines severe as guide lines. – The boundary line and every fifth line is marked with a thick or red line

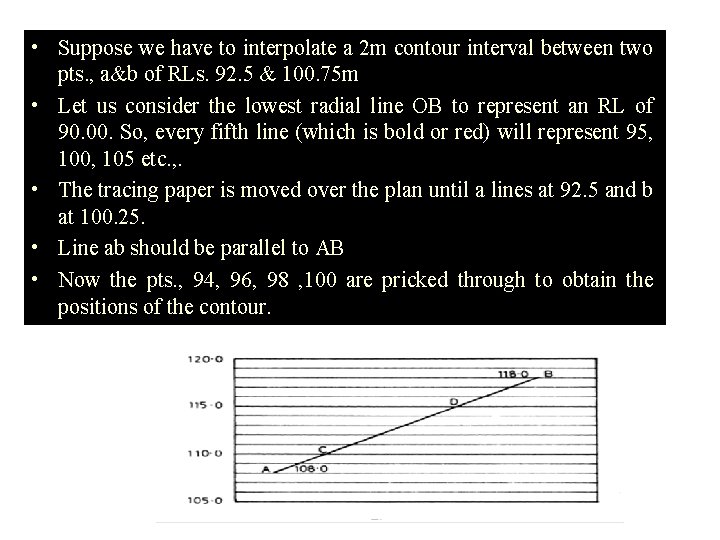
• Suppose we have to interpolate a 2 m contour interval between two pts. , a&b of RLs. 92. 5 & 100. 75 m • Let us consider the lowest radial line OB to represent an RL of 90. 00. So, every fifth line (which is bold or red) will represent 95, 100, 105 etc. , . • The tracing paper is moved over the plan until a lines at 92. 5 and b at 100. 25. • Line ab should be parallel to AB • Now the pts. , 94, 96, 98 , 100 are pricked through to obtain the positions of the contour.

CONTOUR GRADIENT • During preliminary survey for roads in hilly area, the required pts. . , are first established along the gradient. • The line joining these pts. , is known as the contour gradient or grade of contour

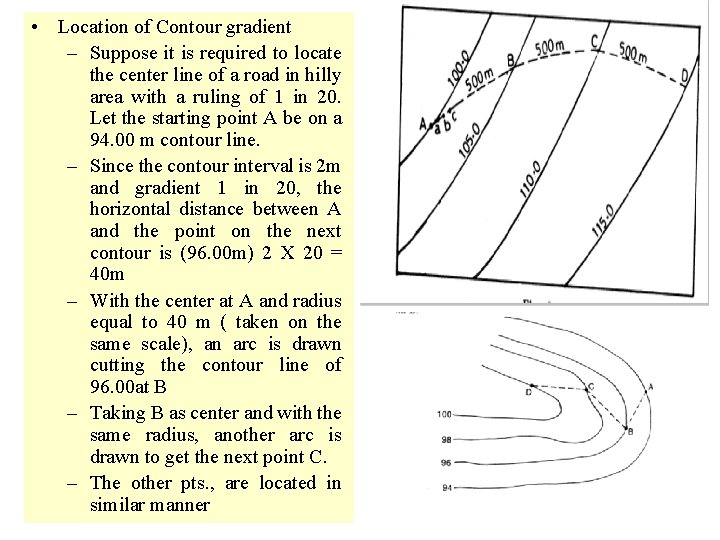
• Location of Contour gradient – Suppose it is required to locate the center line of a road in hilly area with a ruling of 1 in 20. Let the starting point A be on a 94. 00 m contour line. – Since the contour interval is 2 m and gradient 1 in 20, the horizontal distance between A and the point on the next contour is (96. 00 m) 2 X 20 = 40 m – With the center at A and radius equal to 40 m ( taken on the same scale), an arc is drawn cutting the contour line of 96. 00 at B – Taking B as center and with the same radius, another arc is drawn to get the next point C. – The other pts. , are located in similar manner

METHODS OF CONTOUR • A. Direct Method – Case –I – when the area is oblong and can not be controlled from single station. – In this method various pts. , on any contour are located on the ground by taking levels. Then pts. , are marked by pegs. – After this, the pts. , are plotted on the map, to any suitable scale by plane table. – This method is very slow and tedious – But it gives accurate contour lines

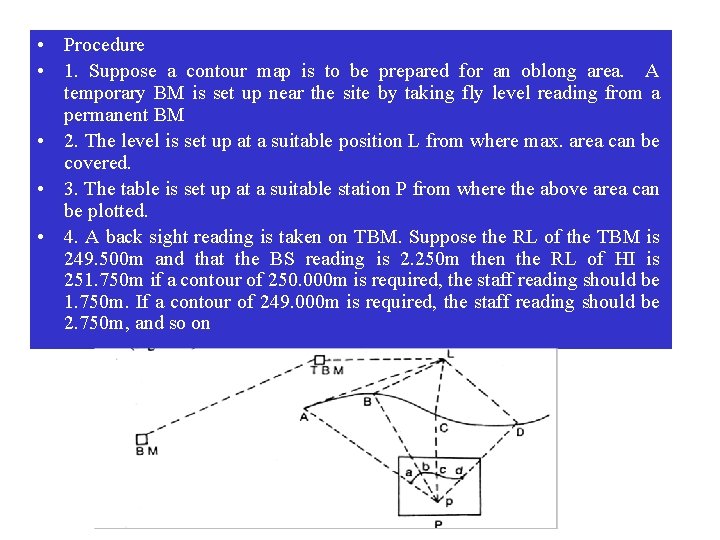
• Procedure • 1. Suppose a contour map is to be prepared for an oblong area. A temporary BM is set up near the site by taking fly level reading from a permanent BM • 2. The level is set up at a suitable position L from where max. area can be covered. • 3. The table is set up at a suitable station P from where the above area can be plotted. • 4. A back sight reading is taken on TBM. Suppose the RL of the TBM is 249. 500 m and that the BS reading is 2. 250 m then the RL of HI is 251. 750 m if a contour of 250. 000 m is required, the staff reading should be 1. 750 m. If a contour of 249. 000 m is required, the staff reading should be 2. 750 m, and so on

• 5. The staff man holds the staff at different pts. , of the area by moving up • • and down, or left and right, until the staff reading is exactly 1. 750. Then the pts. , are marked by pegs. Suppose these pts. , are A, B, C, D 6. A suitable pt. , p is selected on the sheet to represent the suitable P. then with the alidade touching p, rays are drawn to A, B, C, &D. The distance PA, PB, PC & PD are measured and plotted to suitable scale. In this manner, the pts. , a, b, c, &d of the contour line of RL 250. 00 m are obtained. These pts. , are joined to obtain the contour of 250. 000 m Similarly, the pts of the other contours are located When required, the levelling instrument and the plane table are shifted and set up in a new position in order to continue the operation along the oblong area.

• Case – II • When the area is small and can be controlled from single station. In this case, the method of radial lines is adopted to obtain contour map. This is very slow and tedious, but gives actual contour lines • Direct method • 1. The plane table is set up at suitable station P from where the whole area can be measured • 2. A point p is suitably selected on the sheet to represents the station P. Radial lines are then drawn in different directions • 3. A TBM is established near the site. The level is set up at a suitable position L and a BS reading is taken on TBM

• Let the HI in this setting be 153. 250 m. So, to find the contour of RL 152. 000 m a staff reading of 1. 250 m is required at a particular point, so that the RL of contour of that point comes to 152. 000 m • RL = HI – Staff reading = 153. 250 – 1. 250 = 152. 000 m 4. The staff man holds the staff along the rays drawn from the PT station in such a way that the staff reading on that point is exactly 1. 250. in this manner, pts. , A, B, C, D & E are located on the ground, where the staff reading are exactly 1. 250 m 5. The distance PA, PB, PC, PD & PE are measured and plotted to scale. Thus the pts. , a, b, c, d & e are obtained which are joined in order to obtain a contour of 152. 000 6. The other contour may be located in similar fashion

• Indirect method • The RLs of different pts. , are taken at regular intervals along a series of lines set up on the ground. • The position of these pts. , are plotted on a sheet to any scale. • The spot levels are noted at respective pts. , • Then the pts. , of contour lines are found out by interpolation, after which they are joined to get the required contour lines. Although very quick, this method gives only the approximately positions of contour lines

• A) using Cross Section • A base line, center line or profile line is considered. C/s are taken perpendicular to this line at regular intervals • After this, pts. , are marked along the C/s. at a regular intervals. • TBM is set up near the site. • Staff reading are taken along the base line and c/s. note down all the values in field book mentioning the base line and C/s • The RL of each pts. , are calculated. Then the base line and C/s. are plotted to scale. • Subsequently the RLs. Of the respective pts are noted on the map, after which the required contour line is drawn by interpolation.

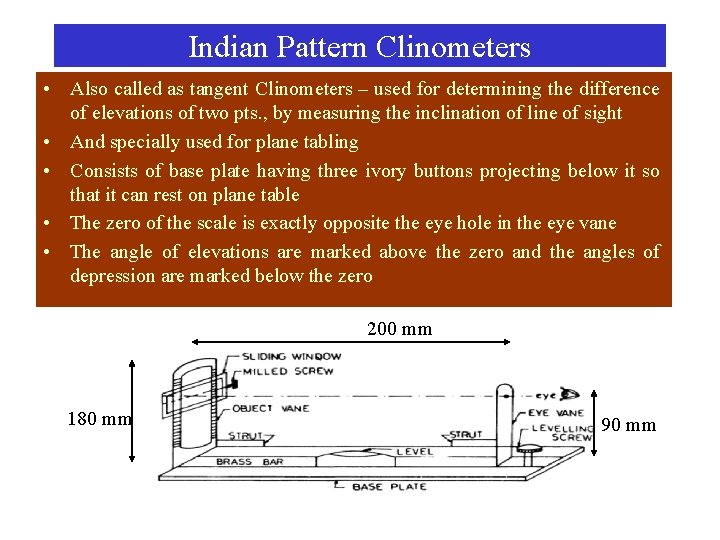
Indian Pattern Clinometers • Also called as tangent Clinometers – used for determining the difference of elevations of two pts. , by measuring the inclination of line of sight • And specially used for plane tabling • Consists of base plate having three ivory buttons projecting below it so that it can rest on plane table • The zero of the scale is exactly opposite the eye hole in the eye vane • The angle of elevations are marked above the zero and the angles of depression are marked below the zero 200 mm 180 mm 90 mm

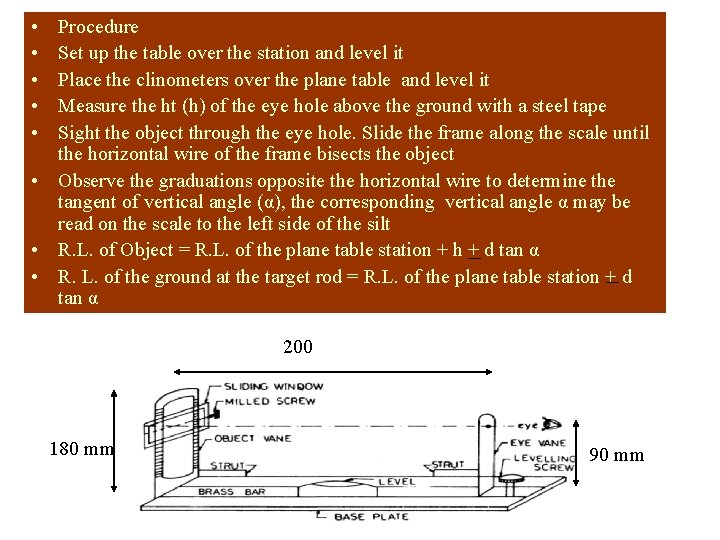
• • • Procedure Set up the table over the station and level it Place the clinometers over the plane table and level it Measure the ht (h) of the eye hole above the ground with a steel tape Sight the object through the eye hole. Slide the frame along the scale until the horizontal wire of the frame bisects the object • Observe the graduations opposite the horizontal wire to determine the tangent of vertical angle (α), the corresponding vertical angle α may be read on the scale to the left side of the silt • R. L. of Object = R. L. of the plane table station + h + d tan α • R. L. of the ground at the target rod = R. L. of the plane table station + d tan α 200 180 mm 90 mm