Contornos Original Sobel T8 Original Sobel T17 Original
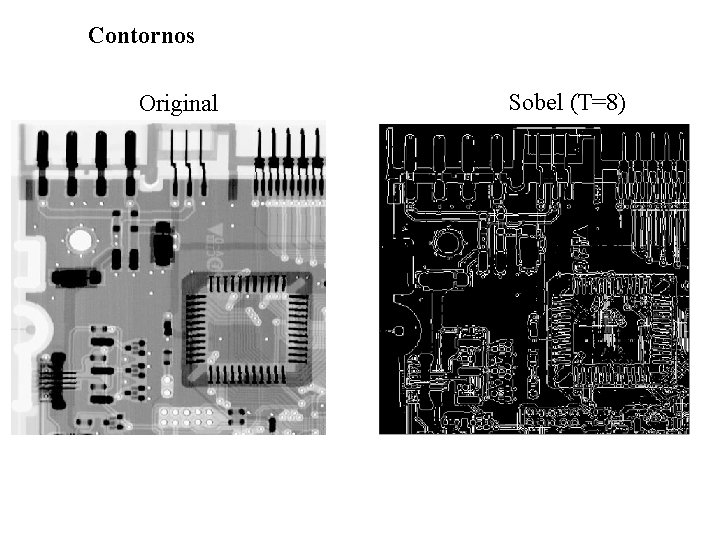
Contornos Original Sobel (T=8)
Original Sobel (T=17)
Original Sobel (T=8)
Original Sobel (T=17)
Laplaciano da Gaussiana (Lo. G) Original sigma=1. 5
Original sigma=2. 0
Original sigma=2. 3
Original sigma=1. 5
Original sigma=2. 0
Original sigma=2. 5
Detector Multiescala • Marr-Hildreth 1 – Convolução de f com uma gaussiana 2 – Cálculo do laplaciano 3 – Os contornos nas diferentes escalas pelo “zero-crossing” do laplaciano. são representados
Assim: com e • é o fator de escala • Convoluções com diferentes podem ser combinadas para formar uma imagem de contornos.
Original Marr-Hildreth (2 escalas): desvios padrões: 1. 2 e 2. 8
Original Marr-Hildreth (2 escalas): desvios padrões: 4. 2 e 5. 8
desvios padrões: 0. 7 e 2. 3 Original desvios padrões: 1. 2 e 2. 8
desvios padrões: 2. 2 e 3. 8 Original desvios padrões: 3. 2 e 4. 8
desvios padrões: 4. 2 e 5. 8 Original desvios padrões: 5. 2 e 6. 8
• Detector de Canny 1 - Suavizar a imagem com uma gaussiana 2 - Computar para cada pixel o gradiente local, e a direção do contorno, , 3 - Um pixel é dito de contorno se a sua magnitude é máxima na direção do gradiente eliminar pontos não-maximais da imagem de gradiente. 4 - Binarizar por histerese a imagem de contornos maximais (dois limiares, T 1 e T 2, com T 1< T 2. Pontos com valores acima de T 2 são ditos “fortes” e pontos com valores entre T 1 e T 2 são ditos “fracos”. A binarização une pontos fracos 8 -conectados a pontos fortes.
![Detector de Canny Original T= [2 13], sigma= 1. 0](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-19.jpg "Detector de Canny Original T= [2 13], sigma= 1. 0")
Detector de Canny Original T= [2 13], sigma= 1. 0
![Original T= [2 13], sigma= 2. 0](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-20.jpg "Original T= [2 13], sigma= 2. 0")
Original T= [2 13], sigma= 2. 0
![Original T= [2 13], sigma= 1. 0](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-21.jpg "Original T= [2 13], sigma= 1. 0")
Original T= [2 13], sigma= 1. 0
![Original T= [2 13], sigma= 1. 5](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-22.jpg "Original T= [2 13], sigma= 1. 5")
Original T= [2 13], sigma= 1. 5
![Original T= [2 13], sigma= 2](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-23.jpg "Original T= [2 13], sigma= 2")
Original T= [2 13], sigma= 2
![Original T= [2 13], sigma= 3](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-24.jpg "Original T= [2 13], sigma= 3")
Original T= [2 13], sigma= 3
![Original T= [2 13], sigma= 5](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-25.jpg "Original T= [2 13], sigma= 5")
Original T= [2 13], sigma= 5
Original Roberts, T=15
Original Sobel, T=15
![Canny, T[12 31], sigma =1 Original](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-28.jpg "Canny, T[12 31], sigma =1 Original")
Canny, T[12 31], sigma =1 Original
Original Roberts, T=10
Original Sobel, T=10
![Original Canny, T[14 35], sigma 1](http://slidetodoc.com/presentation_image_h2/83c75f4133909947a952fea593ab9ff4/image-31.jpg "Original Canny, T[14 35], sigma 1")
Original Canny, T[14 35], sigma 1
- Slides: 31