Continuum finite element modeling of concrete structural components

Continuum finite element modeling of concrete structural components - Nilanjan Mitra

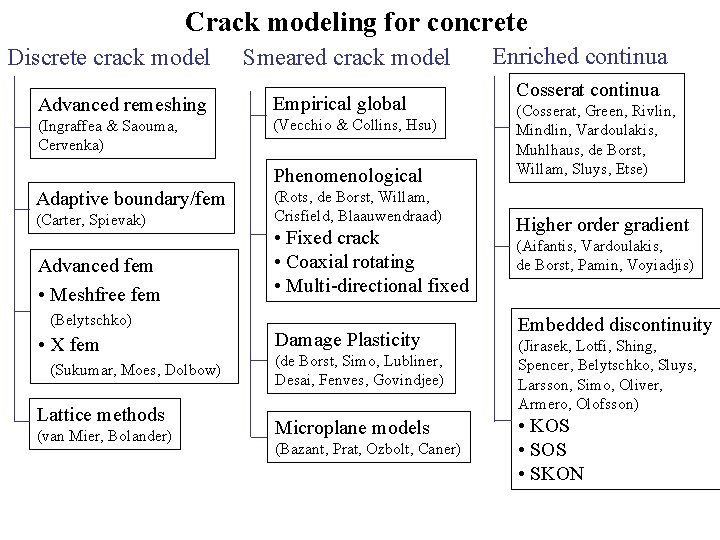
Crack modeling for concrete Discrete crack model Smeared crack model Advanced remeshing Empirical global (Ingraffea & Saouma, Cervenka) (Vecchio & Collins, Hsu) Phenomenological Adaptive boundary/fem (Carter, Spievak) Advanced fem • Meshfree fem (Belytschko) • X fem (Sukumar, Moes, Dolbow) Lattice methods (van Mier, Bolander) (Rots, de Borst, Willam, Crisfield, Blaauwendraad) • Fixed crack • Coaxial rotating • Multi-directional fixed Damage Plasticity (de Borst, Simo, Lubliner, Desai, Fenves, Govindjee) Microplane models (Bazant, Prat, Ozbolt, Caner) Enriched continua Cosserat continua (Cosserat, Green, Rivlin, Mindlin, Vardoulakis, Muhlhaus, de Borst, Willam, Sluys, Etse) Higher order gradient (Aifantis, Vardoulakis, de Borst, Pamin, Voyiadjis) Embedded discontinuity (Jirasek, Lotfi, Shing, Spencer, Belytschko, Sluys, Larsson, Simo, Oliver, Armero, Olofsson) • KOS • SKON

Models done with TNO DIANA

Constitutive models for continuum FEM Compressive model for concrete: • Yield surface – Drucker-Prager • Flow rule -Associative • Compression Hardening/Softening function -- calibrated to match Popovics relation • Plastic strain is zero till 30% of the strength is achieved • Suitable for biaxial loading -- 16% increase in strength Tensile model for concrete: • Linear tension cut-off • Hordijk model for tension softening Model for reinforcement steel: • Associated Von-Mises plasticity with strain hardening Model for bond in between reinforcement and concrete: • Elastic radial response • Transverse response is calibrated to match the Eligehausen model for bond

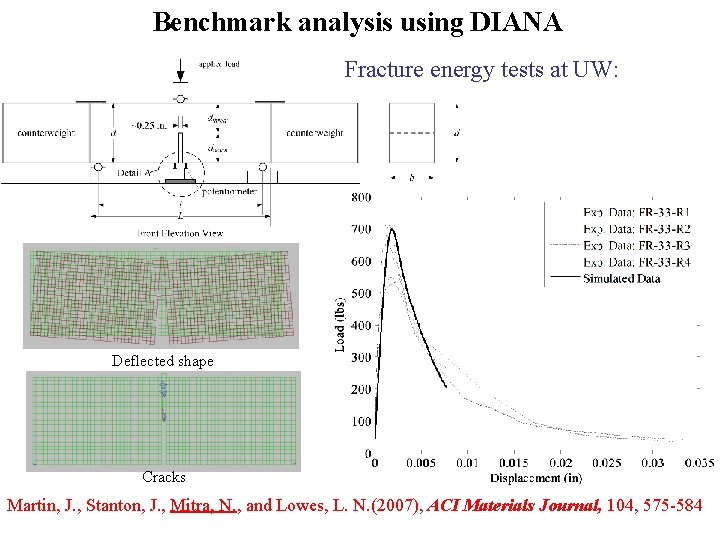
Benchmark analysis using DIANA Fracture energy tests at UW: Deflected shape Cracks Martin, J. , Stanton, J. , Mitra, N. , and Lowes, L. N. (2007), ACI Materials Journal, 104, 575 -584

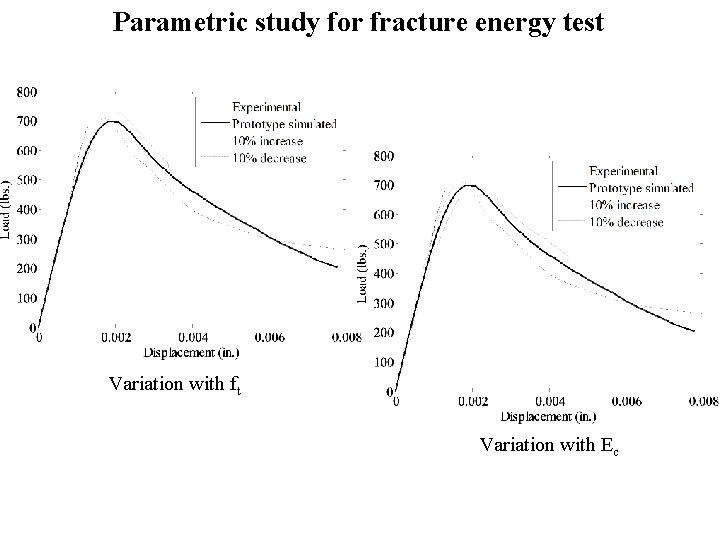
Parametric study for fracture energy test Variation with ft Variation with Ec

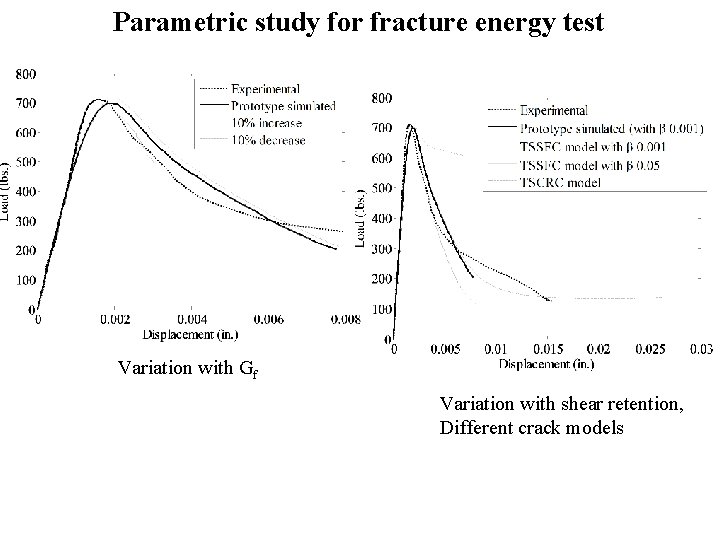
Parametric study for fracture energy test Variation with Gf Variation with shear retention, Different crack models

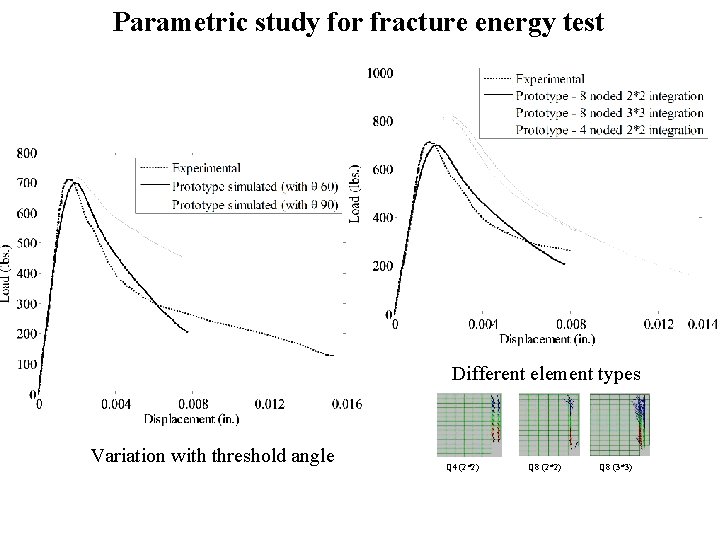
Parametric study for fracture energy test Different element types Variation with threshold angle Q 4 (2*2) Q 8 (3*3)

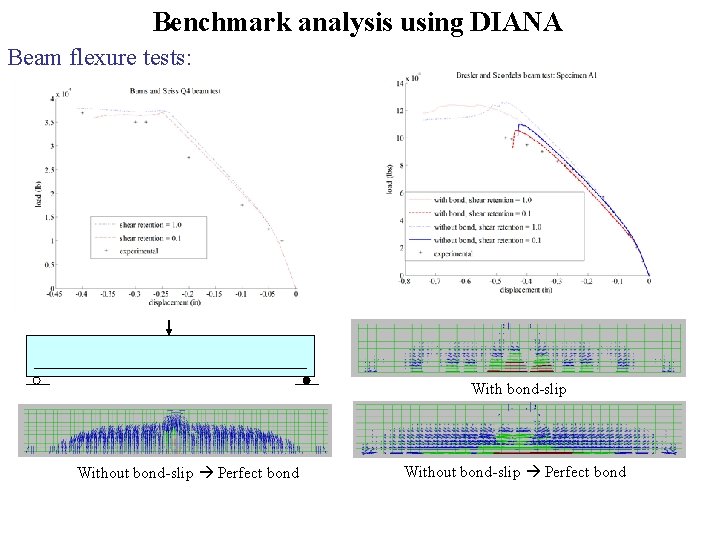
Benchmark analysis using DIANA Beam flexure tests: With bond-slip Without bond-slip Perfect bond

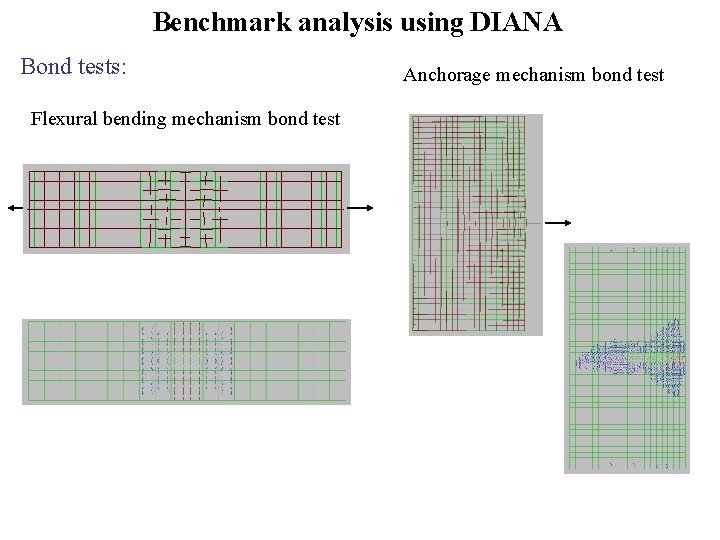
Benchmark analysis using DIANA Bond tests: Flexural bending mechanism bond test Anchorage mechanism bond test

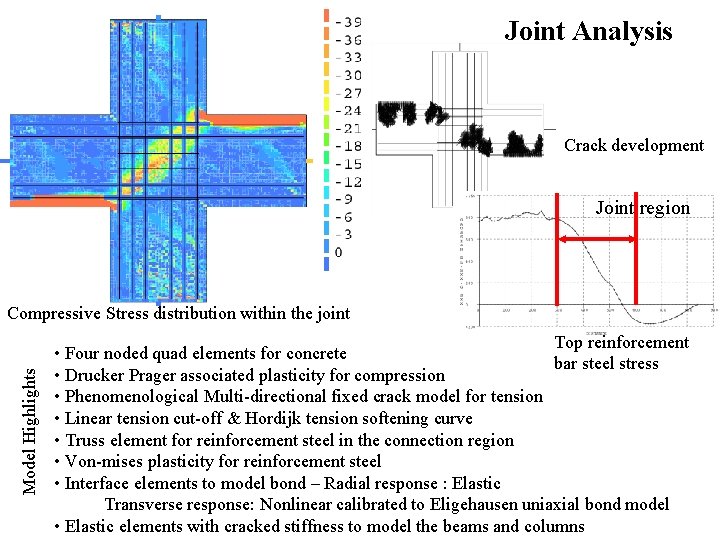
Joint Analysis Crack development Joint region Model Highlights Compressive Stress distribution within the joint Top reinforcement • Four noded quad elements for concrete bar steel stress • Drucker Prager associated plasticity for compression • Phenomenological Multi-directional fixed crack model for tension • Linear tension cut-off & Hordijk tension softening curve • Truss element for reinforcement steel in the connection region • Von-mises plasticity for reinforcement steel • Interface elements to model bond – Radial response : Elastic Transverse response: Nonlinear calibrated to Eligehausen uniaxial bond model • Elastic elements with cracked stiffness to model the beams and columns

Studies carried out with ABAQUS

Model material properties • • Compression stress-strain curve : Popovics equation[1973]. Tension behavior : Mitra [2008]. Linear response : 30% of maximum compressive strength. Concrete model: Concrete Damage Plasticity.

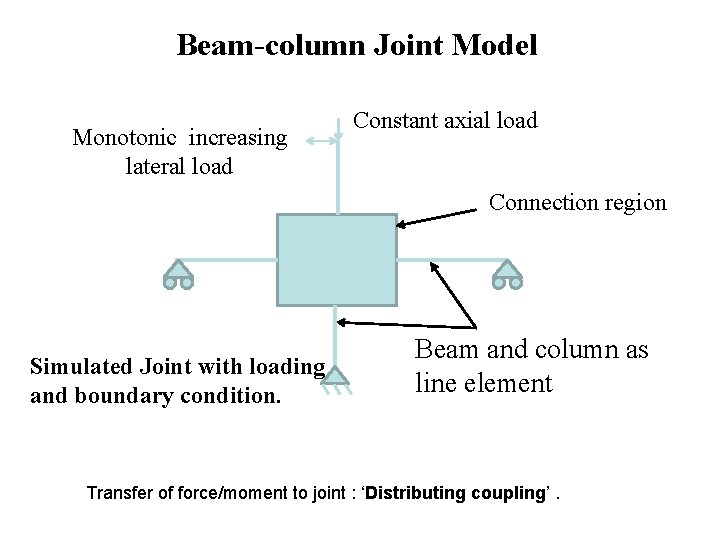
Beam-column Joint Model Monotonic increasing lateral load Constant axial load Connection region Simulated Joint with loading and boundary condition. Beam and column as line element Transfer of force/moment to joint : ‘Distributing coupling’.

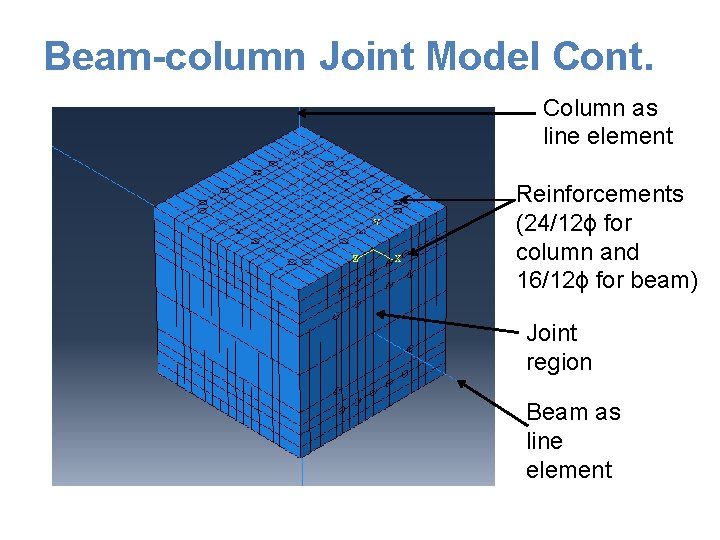
Beam-column Joint Model Cont. Column as line element Reinforcements (24/12ɸ for column and 16/12ɸ for beam) Joint region Beam as line element

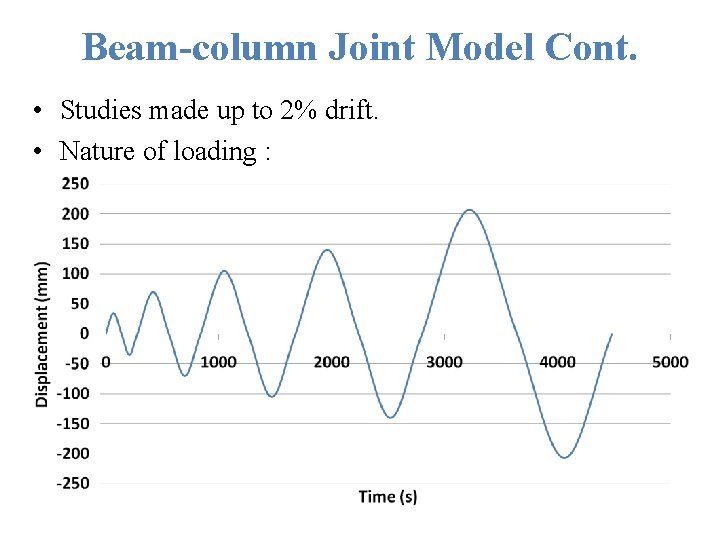
Beam-column Joint Model Cont. • Studies made up to 2% drift. • Nature of loading :

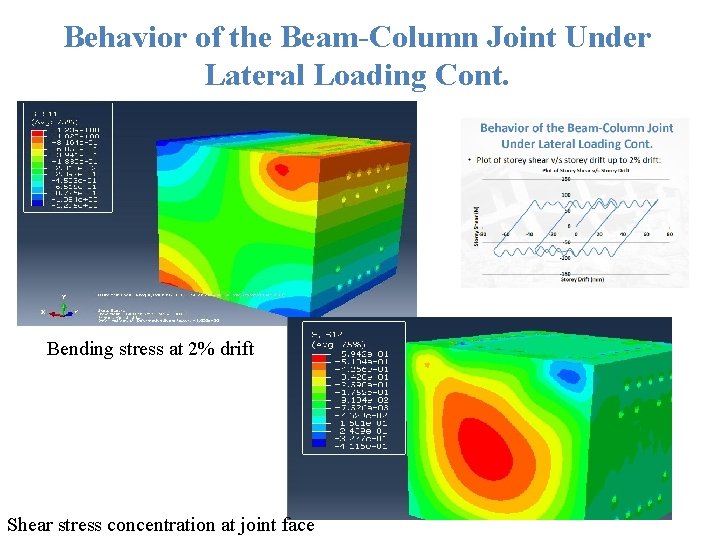
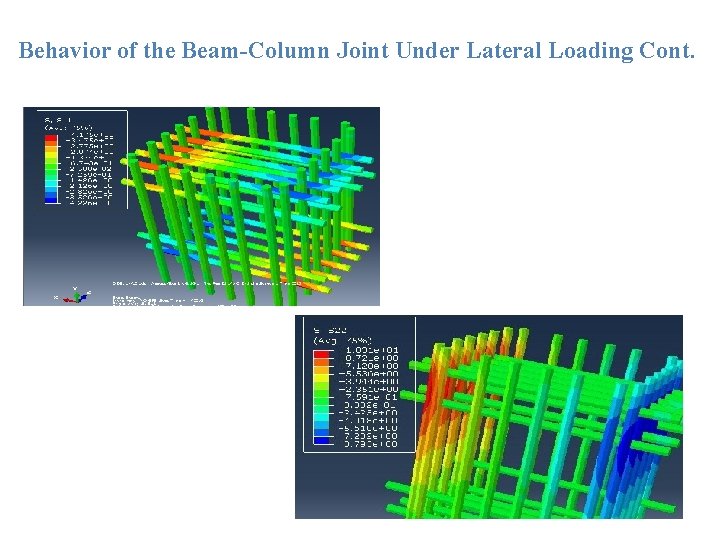
Behavior of the Beam-Column Joint Under Lateral Loading Cont. Bending stress at 2% drift Shear stress concentration at joint face

Behavior of the Beam-Column Joint Under Lateral Loading Cont.

More work pending for 3 d continuum simulation for joints: Looking for students to complete the work Any interested student with some prior expertise in FE modeling, preferably with concrete modeling can contact me in my email add.