Continuum approach to crystal surface morphology evolution Dionisios

Continuum approach to crystal surface morphology evolution Dionisios Margetis Department of Mathematics, M. I. T. June 10, 2005 IMA Workshop on Effective Theories for Materials and Macromolecules

Surfaces of materials evolve Example: Decay (relaxation) of nanostructure Si nanostructure, 465 o. C (Single Tunneling Microscopy, STM) [Ichimiya et al. , Surf. Rev. Lett. (1998)] t=0 crystal surface t=121 sec t t=241 s t=723 s (Universal) Evolution laws and predictions ?

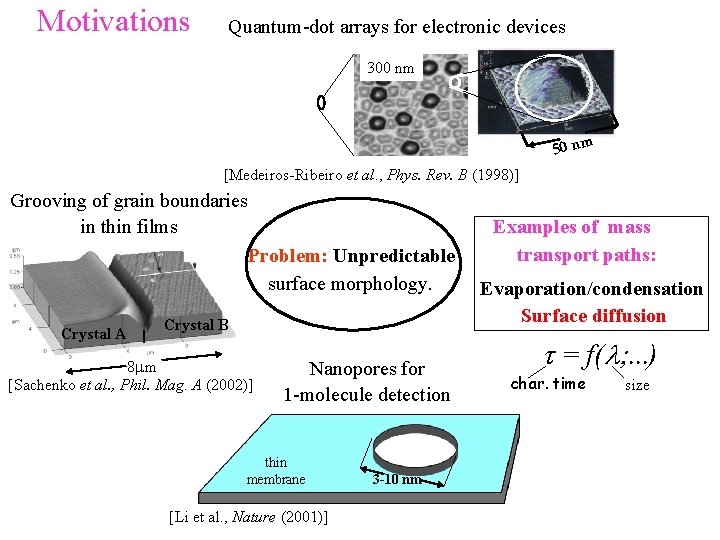
Motivations Quantum-dot arrays for electronic devices 300 nm 50 nm [Medeiros-Ribeiro et al. , Phys. Rev. B (1998)] Grooving of grain boundaries in thin films Problem: Unpredictable surface morphology. 8 mm Crystal A Crystal B 8 mm [Sachenko et al. , Phil. Mag. A (2002)] Nanopores for 1 -molecule detection thin membrane [Li et al. , Nature (2001)] 3 -10 nm Examples of mass transport paths: Evaporation/condensation Surface diffusion t = f(l; . . . ) char. time size

Surface morphology relaxation: ``Classical’’ studies chem. potential height, h (smooth) curvature [Herring, J. Appl. Phys. (1950); Mullins, J. Appl. Phys. (1957)] x Surface diffusion: surface current, Dominates time scale at sufficiently small l 4 surface diffusivity For smaller devices processing is `pushed’ to lower temperatures, T.

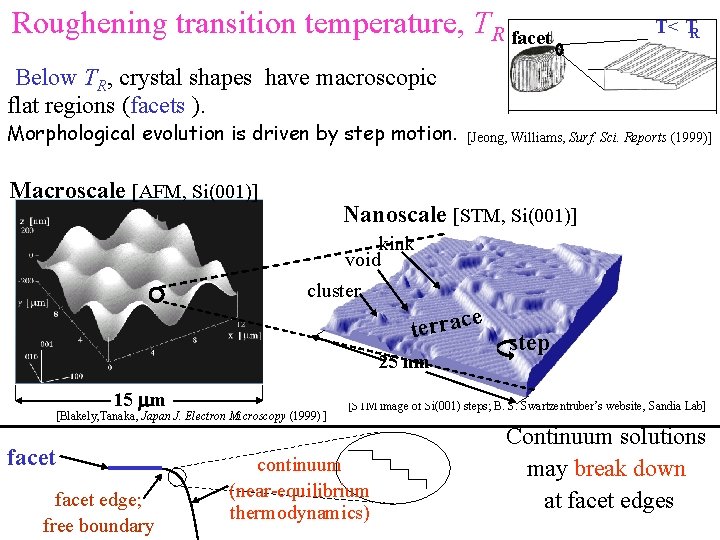
Roughening transition temperature, TR facet Below TR, crystal shapes have macroscopic flat regions (facets ). Morphological evolution is driven by step motion. Macroscale [AFM, Si(001)] T< TR T>TR [Jeong, Williams, Surf. Sci. Reports (1999)] Nanoscale [STM, Si(001)] kink void cluster e terrac 25 nm 15 mm [Blakely, Tanaka, Japan J. Electron Microscopy (1999) ] facet edge; free boundary step [STM image of Si(001) steps; B. S. Swartzentruber’s website, Sandia Lab] continuum (near-equilibrium thermodynamics) Continuum solutions may break down at facet edges

Relaxation experiments: Test theories of step motion? 2 D ripples on Si(001); T = 650 – 750 o. C y lx=0. 4 mm x Surface currents [Erlebacher et al. , Phys. Rev. Lett. (2000)] Peak-to-valley height variation t=2145 s inverse linear decay 5 mm Same decay for ripples on Ag(110) [Pedemonte et al. , Phys. Rev. B (2003)]. ly~10 lx Height profile, h x By contrast, for lithography-based 1 D corrugations on Si(001) [Keefe et al. , J. Phys. Chem. Solids (1994)] : Dpvh= O(e-kt) exponential decay Outline: • Formulation of step motion laws for surface diffusion. • Derivation of continuum evolution equations in (2+1) dims. • Boundary conditions at facets.

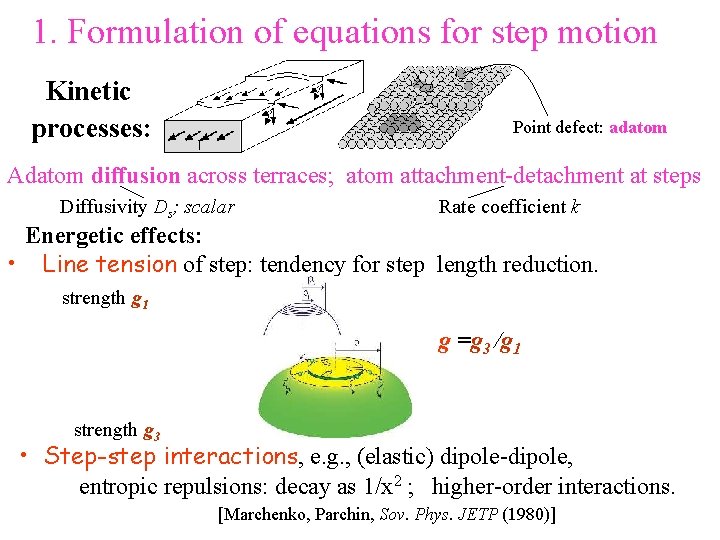
1. Formulation of equations for step motion Kinetic processes: Point defect: adatom Adatom diffusion across terraces; atom attachment-detachment at steps Diffusivity Ds; scalar Rate coefficient k Energetic effects: • Line tension of step: tendency for step length reduction. strength g 1 g =g 3 /g 1 strength g 3 • Step-step interactions, e. g. , (elastic) dipole-dipole, entropic repulsions: decay as 1/x 2 ; higher-order interactions. [Marchenko, Parchin, Sov. Phys. JETP (1980)]

Experiment: step evolution on Pb(111) , T=80 0 C STM imaging; data from K. Thurmer, U. of Maryland NSF-MRSEC [Thurmer et al. , Phys. Rev. Lett. (2001)] facet Top view Layers of atomic height: Top layer Next layer (grey) Surrounding steps 400 nm

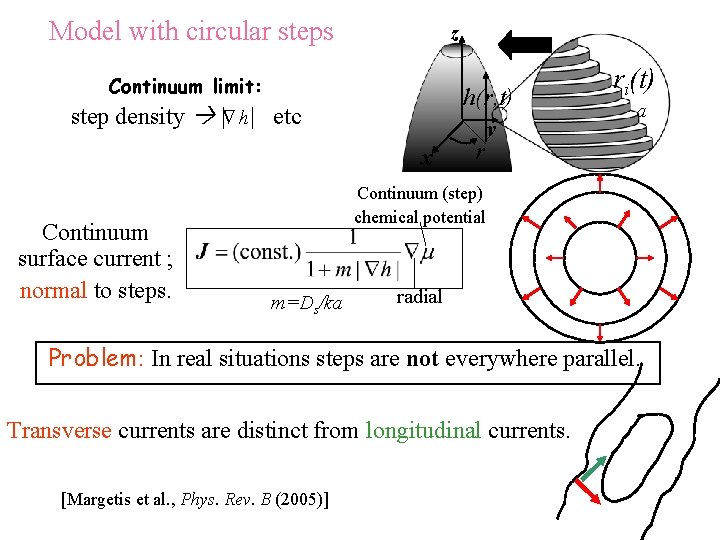
Model with circular steps z Continuum limit: h(r, t) step density | h| etc D x Continuum surface current ; normal to steps. r y ri(t) a Continuum (step) chemical potential m=Ds/ka radial Problem: In real situations steps are not everywhere parallel. Transverse currents are distinct from longitudinal currents. [Margetis et al. , Phys. Rev. B (2005)]

2. Continuum evolution laws in (2+1) dims Step density surface slope= q =| h| Ingredients: ; a/l 0 D mass conservation; from step velocity law Equilibrium adatom density a Step kinetics J= from bc’s at steps [Shenoy et al. , Surface Sci. (2003)] Line tension step chemical potential Step interactions PDE for height h [Margetis, submitted; Margetis, Kohn, in preparation. ] outside facets

Step motion laws in (2+1) dims Local coordinates (h, s); descending steps with height a; ith step at h =hi top terrace es h=hi hi+1 eh ith terrace, hi< h<hi+1 • Step velocity law: Adatom current on ith terrace • Atom adatom density attachment-detachment at steps bounding ith terrace: mi(s, t): step chemical potential [Burton, Cabrera, Frank, Philos. Trans. Roy. Soc. London A (1951)]

• Step chemical potential (incorp. step energetics), mi : [Change in energy of step by adding or removing an atom at (hi, s) ]energy per unit step length ith step moves by: hi +(dh) step length step curvature distance vertical to step energy per unit step length step ``line tension’’ step interactions step density Nearest-neighbor interactions Difficulty: Solving Laplace’s eqn. for Ci on i th terrace. Assumption: h is ``fast’’ and s is ``slow’’ Ci in closed form [E, Yip, J. Stat. Phys. (2001)] [Margetis, preprint (submitted); Margetis, Kohn, in preparation]

From bc’s at step edges Adatom current in continuum limit: hi+1 -hi 0; use of boundary conditions at steps longitudinal current transverse current from Ci~Cieq, h=hi Fluxes parallel and transverse to steps have different effective `` mobilities’’

2. Continuum evolution laws in (2+1) dims Step density surface slope= q =| h| Ingredients: ; a/l 0 D mass conservation; from step velocity law Equilibrium adatom density a Step kinetics J= from bc’s at steps [Shenoy et al. , Surface Sci. (2003)] Line tension step chemical potential Step interactions PDE for height h Elastic dipole-dipole repulsive interactions: V=q 2 outside facets [Margetis, submitted. ]

Surface-free energy approach Surface free energy per unit projected area mobility tensor PDE for h

Line tension Step interactions Material prmt. , (Length)4/Time Cartesian coordinates : mobility tensor A 2 • Step energetics, m ; line tension and step interactions • Step kinetics, m | h| , m=2 Ds /(ka) • Aspect ratio, hy/hx=A; for periodic profiles A~lx/ly A D Take A<1

Decaying bi-directional profiles • Ni(001) lithography corrugations, T~1219 o. C [Maiya, Blakely, J. Appl. Phys. (1967)]; h(x, y, t) ~ H(x, y) e-k t f • Si(001) lithgr. corrugations, T= 800 -1100 o. C, [Keefe, Umbach, Blakely, J. Phys. Chem. Solids (1994)] Evidence by simulations for 1 D sinusoidal initial profiles: Israeli, Kandel, Phys. Rev. B (2000) lx/ly ~10 -3 • Si(001) ripples, T=650 -750 o. C 10 mm [Erlebacher et al. , Phys. Rev. Lett. (2000)]; • Ag(110) ripples, T=200 -230 K [Pedemonte et al. , Phys. Rev. B (2003)]. x h(x, y, t) ~ H(x, y) t -1 y lx/ly ~ 0. 1

Understanding of relevant solutions of PDE is incomplete. Do separable solutions arise, and if so under what conditions? Numerical evidence for initial sinusoidal profiles in 2 D by Shenoy et al. , Phys. Rev. Lett. (2004) Assumptions and plausible scaling scenario: 2 Ds/(ka) • Step interactions dominate over line tension • Attachment-Detachment of adatoms is slowest process: m | h|typ >> 1 D (2 Ds /k)/(terrace width) small Ansatz: h(x, y, t)~T(t) H(x, y) A 2>> (m| h|typ)-1 T(t)=T 0 (1+b t)-1 D Consistent with sputter-rippling experiments A 0 (1 D) : T(t)=T 0 exp(-qt) A=hy/hx ~lx/ly<1 [Margetis, submitted] Consistent with lithography experiments

3. Boundary conditions at facet edge v … facet Example: Axisymmetric shape steps …continuum r 2 r 1 bc’s at moving boundary? ri ri+1 y x g 1: step line tension g 3: strength of step interactions g =g 3/g 1, m=Ds/ka Solutions for ri(t) PDE ü Diffusion-Limited (DL) kinetics: Terrace diffusion is rate-limiting process, m 0 PDE: a r h(r, t) g [Margetis, Fok, preprint] r>w (outside facet)

Choices of boundary conditions for PDE ``Thermodynamic’’ (thrmd) bc’s: ``Layer-drop’’ (ld) conditions: • Height continuity, h(w, t)=hf(t) • Slope continuity • Current continuity, j=jf • Same m : step chemical hf (tn)-hf(tn+1)=a potential outside facet • μ is extended continuously on facet e lac p re time of top-step nth collapse step height Non-local in time condition (h, j , m) = m) (h f, j f , f 0 = e p w slo hf(t) Need to know sequence tn r + Conditions at ``infinity’’ [Spohn, J. Phys. I (France), 1993; Margetis et al. , Phys. Rev. B, 2004] [Israeli, Kandel, Phys. Rev. B (1999); Margetis, Fok, preprint (2005)]

Study of bc’s at facets: Self-similar shapes, long t Numerical solution of step-motion eqns : F(r, t)~T(t) Q(c) : step density c=r t -b : similarity variable; Initial conical shape: T(t)=1 Data collapse by scaling; from step-motion simulations Q(c) F(r, t) tn r tn+6 r unscaled data c=r t -b, cone: b=1/4 For initial shapes h(r, 0)=k rn : T(t)=tc; b, c: rational functions of n. facet [Cone: Israeli, Kandel, Phys. Rev. B (1999); Other shapes: Fok, Margetis, Rosales, in preparation]

Large-n asymptotics of collapse times: tn~ t*. nq t*=t*(g, k, n); q: rational function of v Cone: F(r, t)=F(c=r (Bt) -1/4), q=4 PDE ODE Layer-drop bc: 1 adjustable parameter, t* facet hf(t) ODE+``Thrmd bc’s’’ ODE+``Ld bc’’ w Universal Scaling of profile with g?

Singular perturbation, g=e: small: arb. initial shape facet Boundary layer, F=0 d w e >0 : Ansatz near facet edge, ``Inner’’ solution ~ boundary-layer width PDE universal ODE [Margetis, Aziz, Stone, Phys. Rev. B (2004)]

Solution of universal ODE; f 0(0)=0, f 0( )=1 c 3=c 3(c 1; e), from bc’s Obtain scaling of Fpeak with g=e Same scaling for both sets of bc’s: m=finite as r w+ f 0 Singularity at h = 0 (facet edge) Need to relate c 1, c 3 and ε; apply set of bc’s

Scaling with g (DL kinetics) [Margetis, Aziz, Stone, Phys. Rev. B (2004)] Fpeak : our prediction : Simulations, [Israeli, Kandel, Phys. Rev. B (1999)] = for cone xpeak-x 0

One more prediction for initial cone: w (t; e=0)-w(t; e)=O(e 1/3)>0 facet w [Margetis, Aziz, Stone, Phys. Rev. B (2005)] 8

Another physical limit: Attachment-Detachment Limited kinetics (m=2 Ds/ka ) Ansatz for ``long’’ times: PDE d=O(e 3/8) boundary-layer width [Margetis, Aziz, Stone, Phys. Rev. B (2005)]

Extensions of continuum theory (from step motion laws) • Line tension dependence on angle with crystallographic axis y Continuum: f [Margetis, Kohn, in preparation] step g=g(f) • Deposition of material from above. Flux F [1/(length)2/time] a w terrace width, w • Atom diffusion along steps [Margetis, Kohn, in preparation] [Margetis, Aziz, Stone, in preparation] x

Epilogue-Messages • Continuum evolution eqn in (2+1) dims. Interplay : step kinetics & energetics, surface topography Unification of profile decay observations ? • Boundary conditions at facets are non-local in time; understanding within continuum for axisymm. shapes & similarity: connection with asymptotics of collapse times. Dependence of collapses on step parameters for axisymm. ? ``Early-time’’ collapses and profiles w/ axisymm. ? Extensions to (2+1) dimensions? • Universal scaling of axisym. profiles with step interactions in continuum; agreement with step eqs for class of bc’s.

Acknowledgments : • R. V. Kohn (Courant Institute, NYU). • R. R. Rosales and grad. student P. -W. Fok (Dept. of Mathematics, MIT). • M. J. Aziz and H. A. Stone (DEAS, Harvard). • R. E. Caflisch (Dept. of Mathematics, UCLA, and California Nanosystems Institute). • J. Erlebacher (Materials, Johns Hopkins).

Example: Step-flow equations for circular steps Step velocity …. i-th terrace r adatom current r 1 … a …. . Adatom density diffusion across terraces attach. -detach at steps (b. c. ’s at r=ri, ri+1) step chem. potential line tension step-step interactions Elastic dipole-dipole interactions Eqs of motion for ri(t) [Israeli, Kandel, Phys. Rev. B (1999); Margetis, Aziz, Stone, Phys. Rev. B (2005), in press] ri

STM image of terraces (width about 100 Angstroms) , separated by steps (kinks evident) Roughening temperature depends on surface orientation: (001) (110) (113) Pimpinelli & Villain, Physics of Crystal Growth (1998) 1190 C 1370 C 1340 C