ContinuousTime Fourier Transform Content l Introduction l Fourier














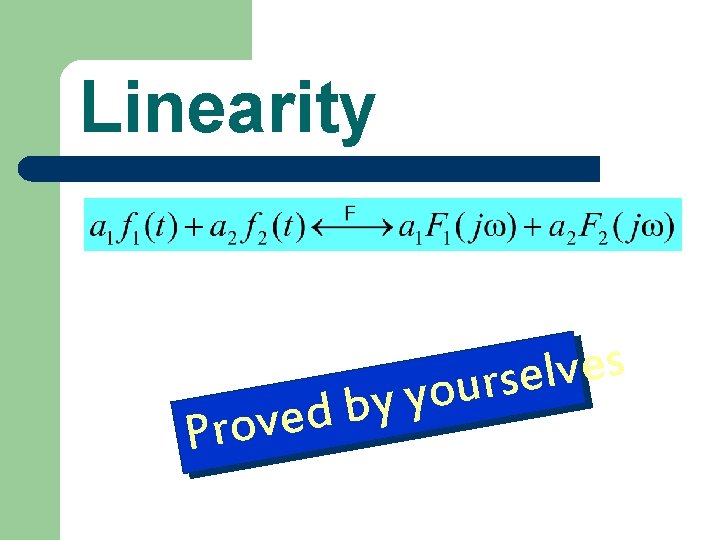















![Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-45.jpg)
![Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-46.jpg)














- Slides: 68

Continuous-Time Fourier Transform 主講者:虞台文

Content l Introduction l Fourier Integral l Fourier Transform l Properties of Fourier Transform l Convolution l Parseval’s Theorem

Continuous-Time Fourier Transform Introduction

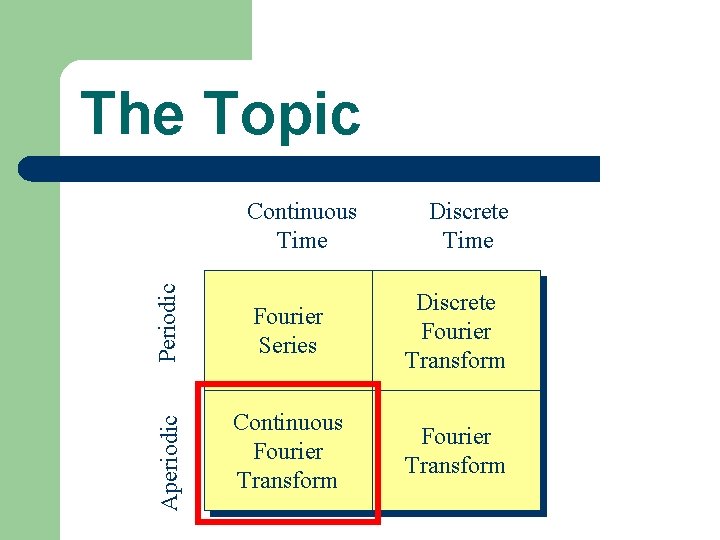
The Topic Aperiodic Periodic Continuous Time Discrete Time Fourier Series Discrete Fourier Transform Continuous Fourier Transform

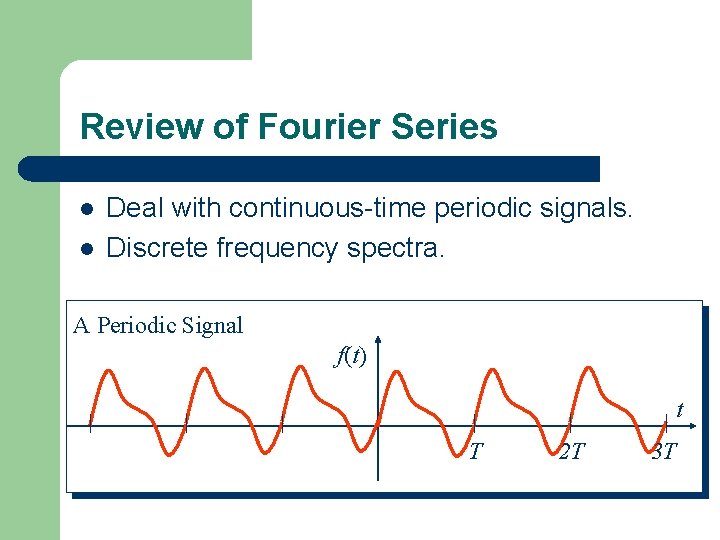
Review of Fourier Series l l Deal with continuous-time periodic signals. Discrete frequency spectra. A Periodic Signal f(t) t T 2 T 3 T

Two Forms for Fourier Series Sinusoidal Form Complex Form:

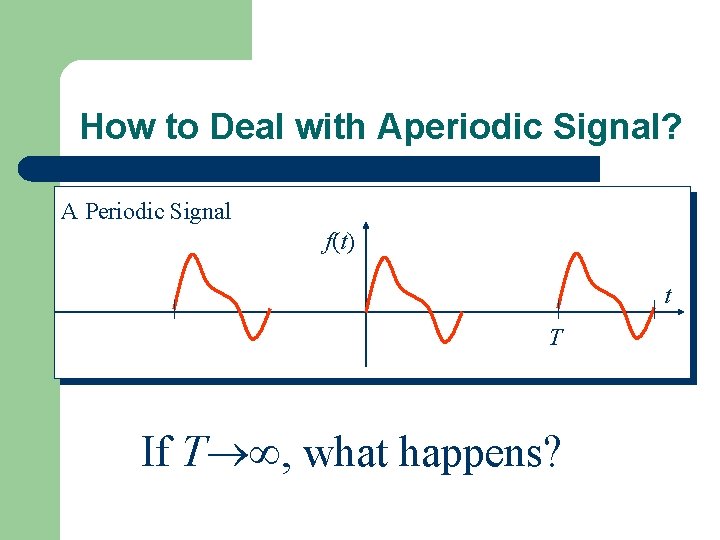
How to Deal with Aperiodic Signal? A Periodic Signal f(t) t T If T , what happens?

Continuous-Time Fourier Transform Fourier Integral

Fourier Integral Let

Fourier Integral F(j ) Synthesis Analysis

Fourier Series vs. Fourier Integral Fourier Series: Period Function Discrete Spectra Fourier Integral: Non-Period Function Continuous Spectra

Continuous-Time Fourier Transform

Fourier Transform Pair Inverse Fourier Transform: Synthesis Fourier Transform: Analysis

Existence of the Fourier Transform Sufficient Condition: f(t) is absolutely integrable, i. e. ,

Continuous Spectra FI(j ) | ) j |F ( ( ) FR(j ) Magnitude Phase

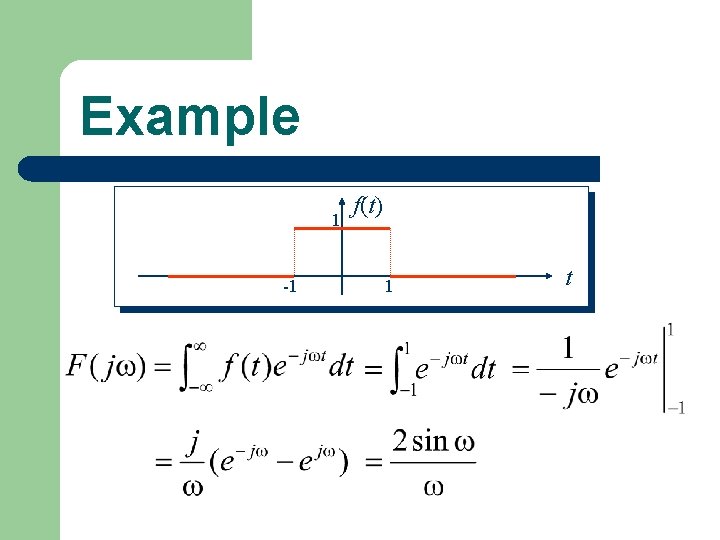
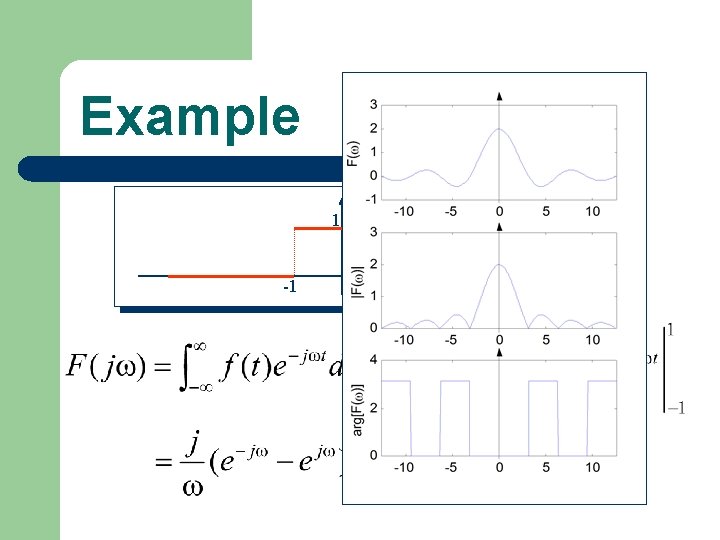
Example 1 -1 f(t) 1 t

Example 1 -1 f(t) 1 t

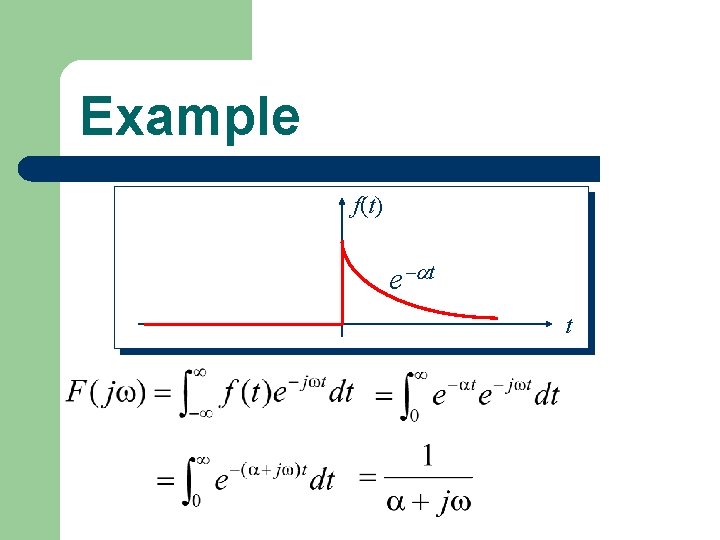
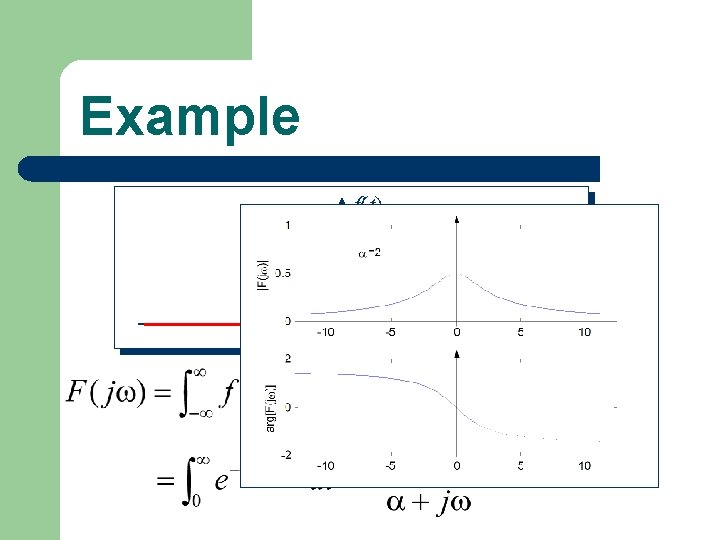
Example f(t) e t t

Example f(t) e t t

Continuous-Time Fourier Transform Properties of Fourier Transform

Notation
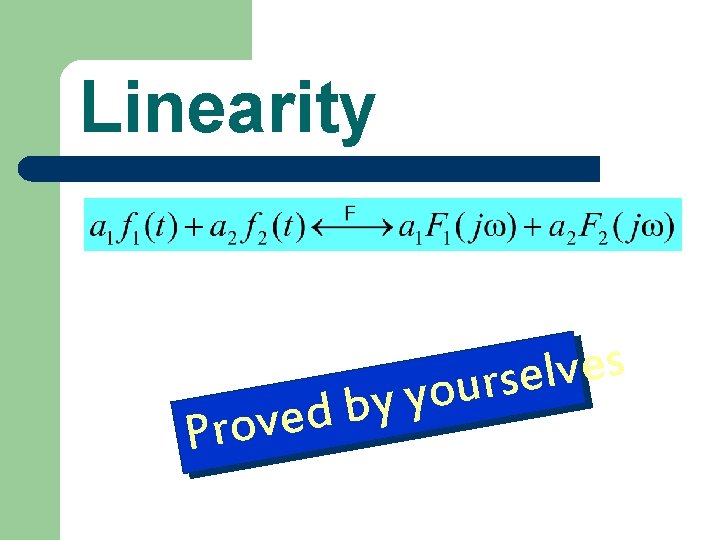
Linearity y b d e v o r P s e v l e s r u yo

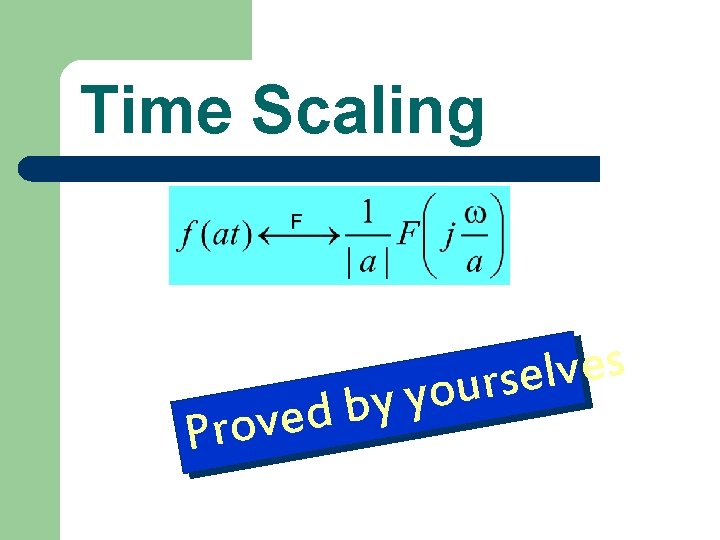
Time Scaling y b d e v o r P s e v l e s r u yo

Time Reversal Pf)

Time Shifting Pf)

Frequency Shifting (Modulation) Pf)

Symmetry Property Pf) Interchange symbols and t

Fourier Transform for Real Functions If f(t) is a real function, and F(j ) = FR(j ) + j. FI(j ) F( j ) = F*(j )

Fourier Transform for Real Functions If f(t) is a real function, and F(j ) = FR(j ) + j. FI(j ) F( j ) = F*(j ) FR(j ) is even, and FI(j ) is odd. FR( j ) = FR(j ) FI( j ) = FI(j ) Magnitude spectrum |F(j )| is even, and phase spectrum ( ) is odd.

Fourier Transform for Real Functions If f(t) is real and even F(j ) is real If f(t) is real and odd F(j ) is pure imaginary Pf) Even Pf) Odd Real

Example: Sol)

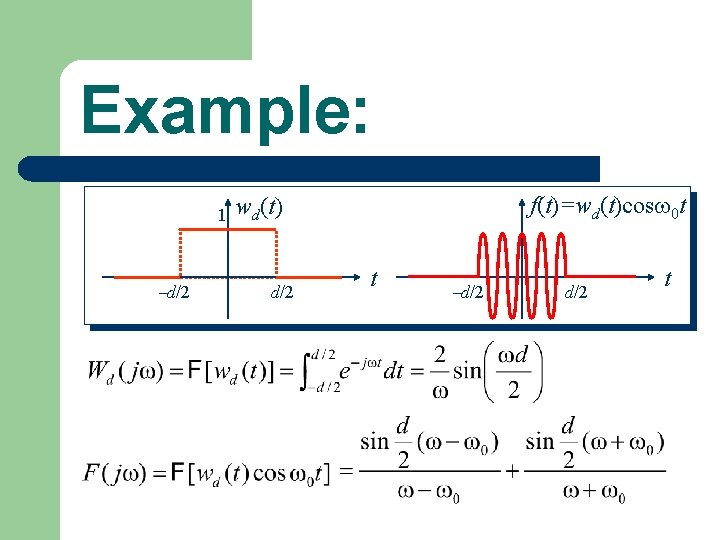
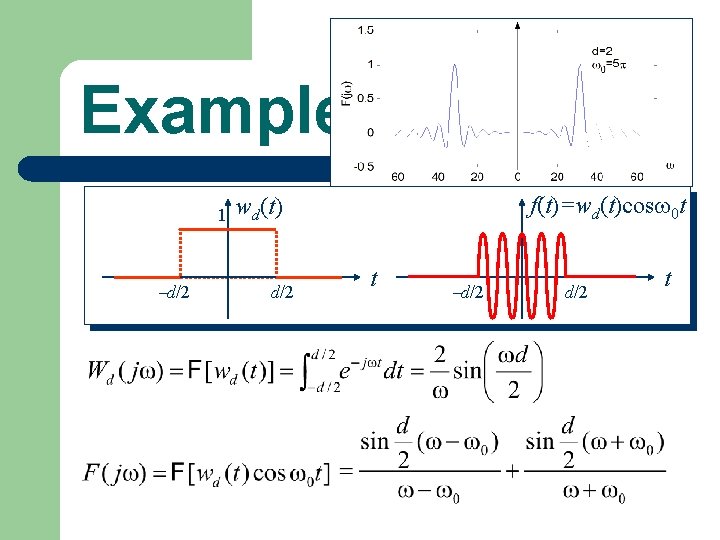
Example: 1 d/2 f(t)=wd(t)cos 0 t wd(t) d/2 t

Example: 1 d/2 f(t)=wd(t)cos 0 t wd(t) d/2 t

1 Example: Sol) wd(t) t d/2

Fourier Transform of f’(t) Pf)

Fourier Transform of f y b d e v o r P (n)(t) s e v l e s r u yo

Fourier Transform of f y b d e v o r P (n)(t) s e v l e s r u yo

Fourier Transform of Integral Let

The Derivative of Fourier Transform Pf)

Continuous-Time Fourier Transform Convolution

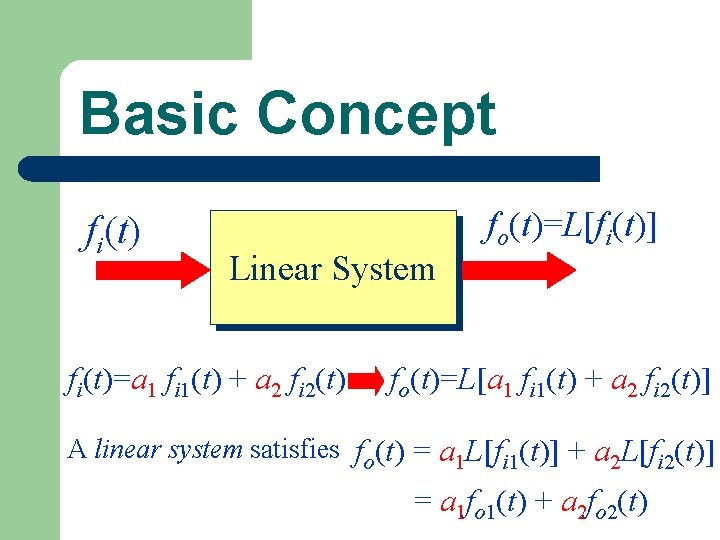
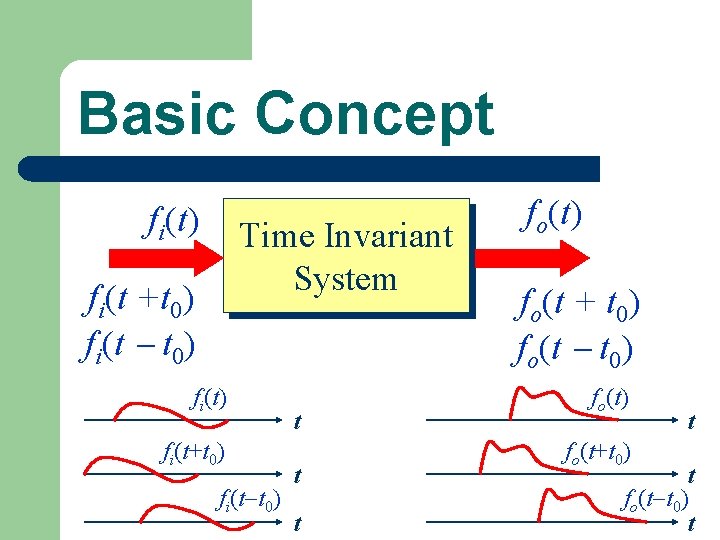
Basic Concept fi(t) Linear System fi(t)=a 1 fi 1(t) + a 2 fi 2(t) fo(t)=L[fi(t)] fo(t)=L[a 1 fi 1(t) + a 2 fi 2(t)] A linear system satisfies fo(t) = a 1 L[fi 1(t)] + a 2 L[fi 2(t)] = a 1 fo 1(t) + a 2 fo 2(t)

Basic Concept fi(t) Time Invariant System fi(t +t 0) fi(t t 0) fi(t+t 0) fi(t t 0) t t t fo(t) fo(t + t 0) fo(t+t 0) t t fo(t t 0) t

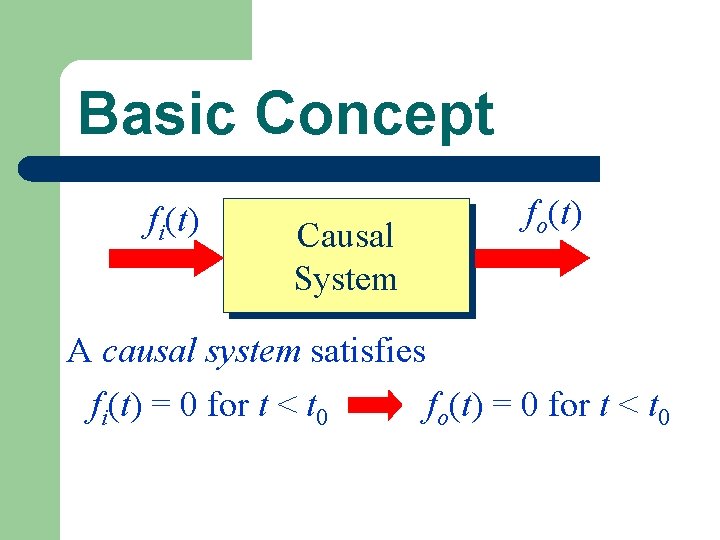
Basic Concept fi(t) Causal System fo(t) A causal system satisfies fi(t) = 0 for t < t 0 fo(t) = 0 for t < t 0

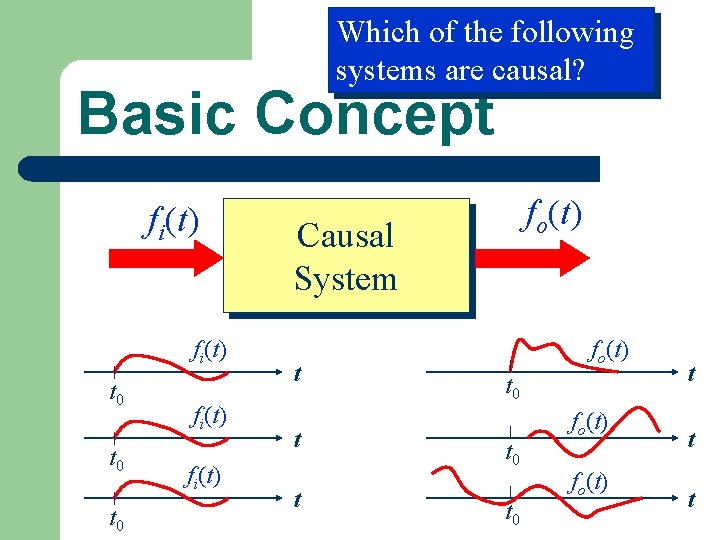
Which of the following systems are causal? Basic Concept fi(t) t 0 t 0 fi(t) fo(t) Causal System t t t fo(t) t 0 t 0 fo(t) t t t
![Unit Impulse Response t ft LTI System htL t Lft Facts Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-45.jpg)
Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution
![Unit Impulse Response t ft LTI System htL t Lft Facts Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-46.jpg)
Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution

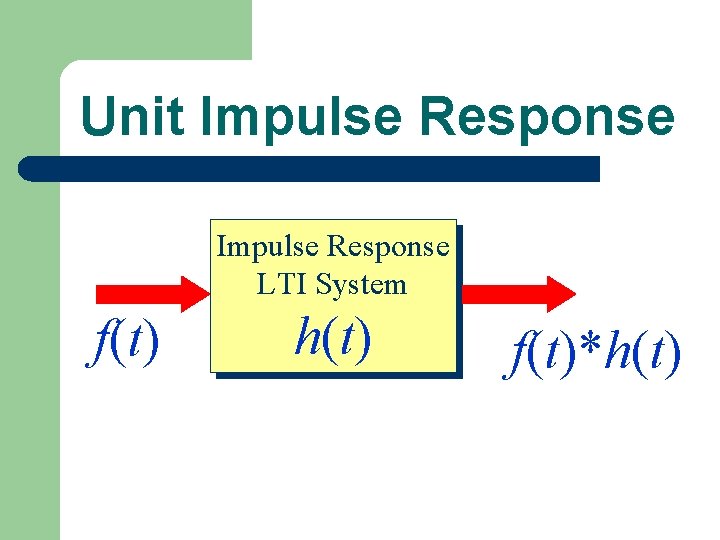
Unit Impulse Response LTI System f(t) h(t) f(t)*h(t)

Convolution Definition The convolution of two functions f 1(t) and f 2(t) is defined as:

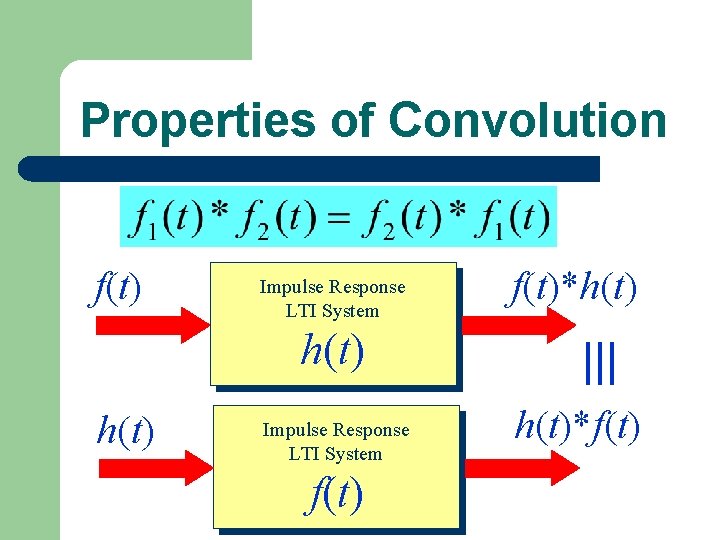
Properties of Convolution

Properties of Convolution f(t) Impulse Response LTI System f(t)*h(t) Impulse Response LTI System f(t) h(t)*f(t)

Properties of Convolution P y y b e v ro s e v l e s r ou

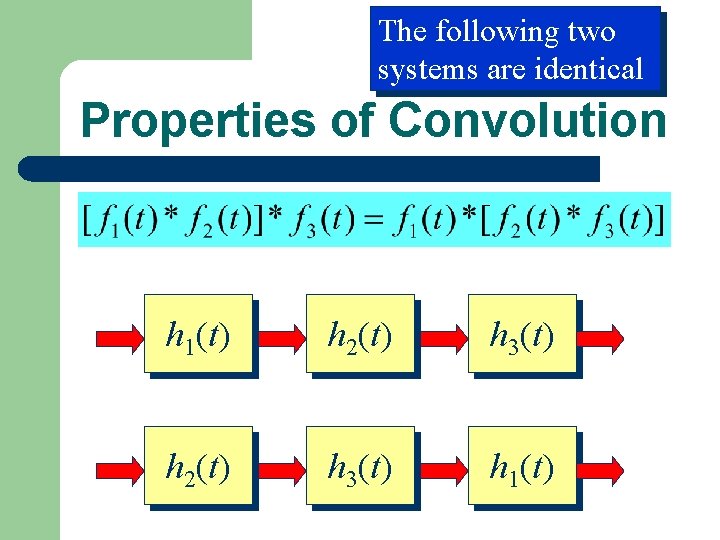
The following two systems are identical Properties of Convolution h 1(t) h 2(t) h 3(t) h 1(t)

Properties of Convolution f(t) f(t)

Properties of Convolution f(t) f(t)

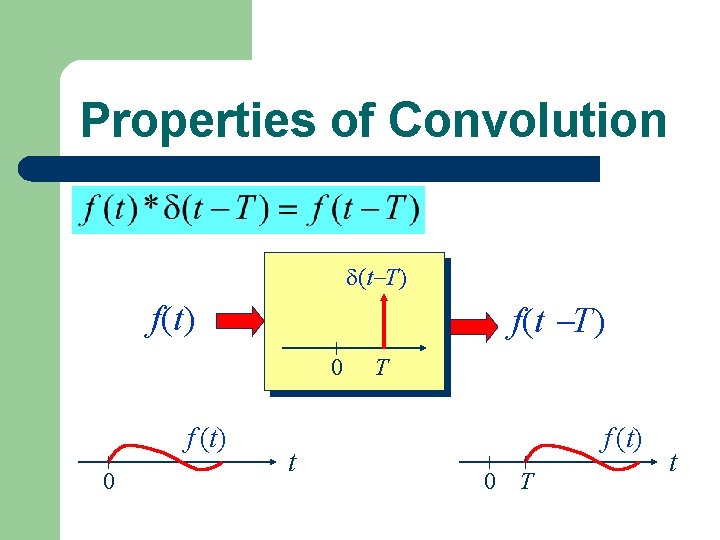
Properties of Convolution (t T) f(t) 0 f (t) 0 t T f (t) 0 T t

System function (t T) serves as an ideal delay or a copier. Properties of Convolution (t T) f(t) 0 f (t) 0 t T f (t) 0 T t

Properties of Convolution

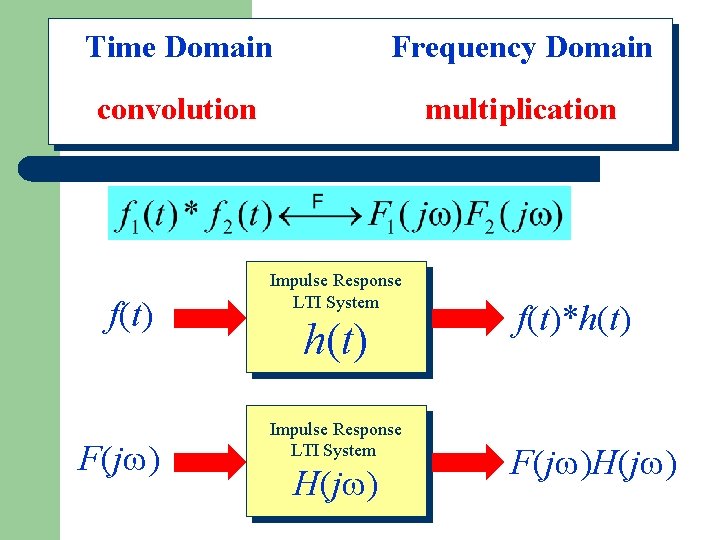
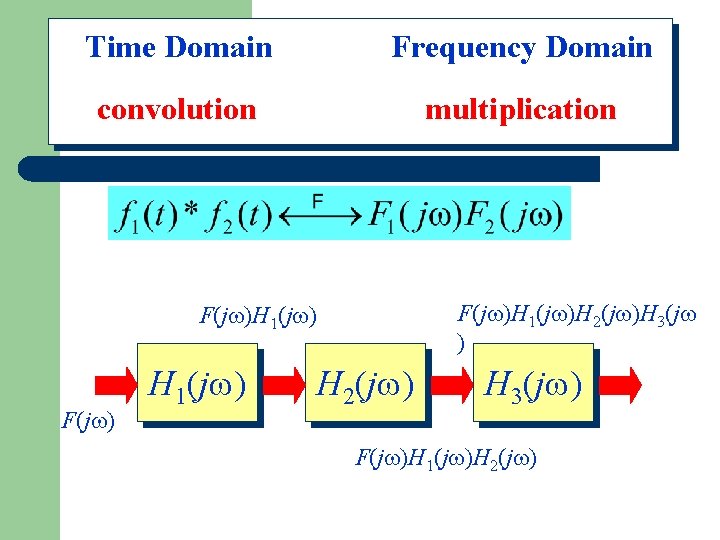
Time Domain Frequency Domain convolution multiplication Properties of Convolution

Time Domain Frequency Domain convolution multiplication Properties of Convolution f(t) F(j ) Impulse Response LTI System h(t) Impulse Response LTI System H(j ) f(t)*h(t) F(j )H(j )

Time Domain Frequency Domain convolution multiplication Properties of Convolution F(j )H 1(j )H 2(j )H 3(j ) F(j )H 1(j ) F(j ) H 1(j ) H 2(j ) H 3(j ) F(j )H 1(j )H 2(j )

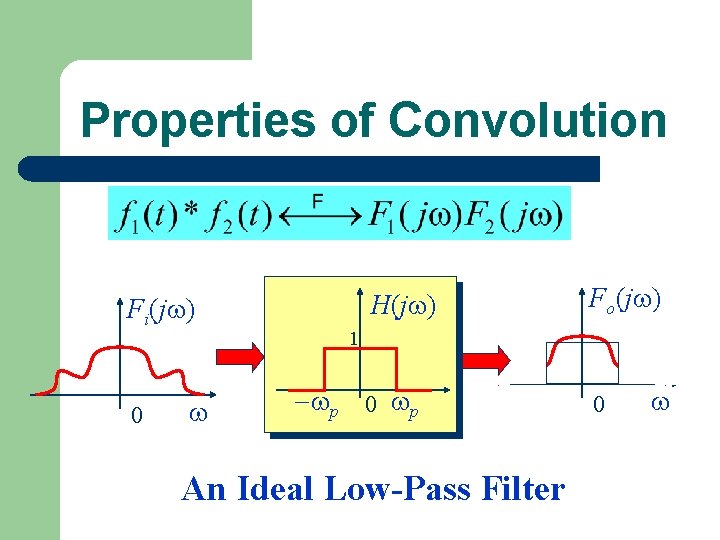
Properties of Convolution Fi(j ) 0 H(j ) Fo(j ) 1 p 0 p An Ideal Low-Pass Filter 0

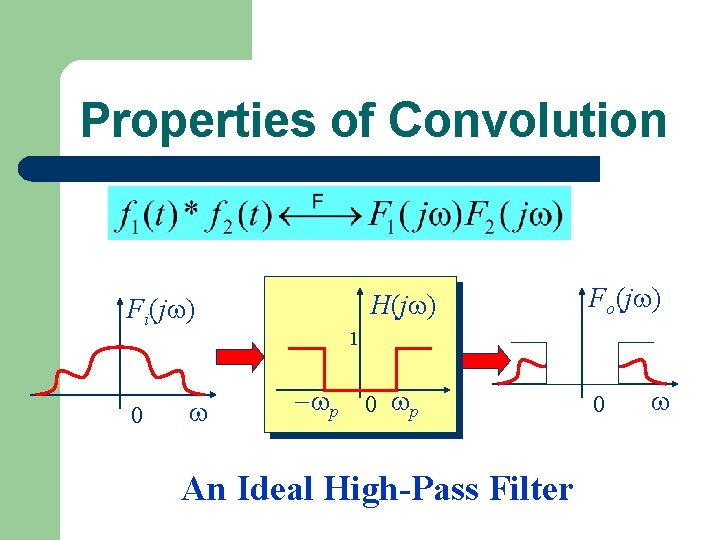
Properties of Convolution Fi(j ) 0 H(j ) Fo(j ) 1 p 0 p An Ideal High-Pass Filter 0

Properties of Convolution s e v l e s r u o Prove by y

Time Domain multiplication Frequency Domain convolution Properties of Convolution s e v l e s r u o Prove by y

Continuous-Time Fourier Transform Parseval’s Theorem

Properties of Convolution =0

Properties of Convolution If f 1(t) and f 2(t) are real functions, f 2(t) real

Parseval’s Theorem: Energy Preserving