Continuous symmetries and approximate quantum error correction ar













- Slides: 40

Continuous symmetries and approximate quantum error correction ar. Xiv: 1902. 07714 Sepehr Nezami Stanford University Philippe Faist, Victor V. Albert, Grant Salton, Fernando Pastawski, Patrick Hayden, John Preskill

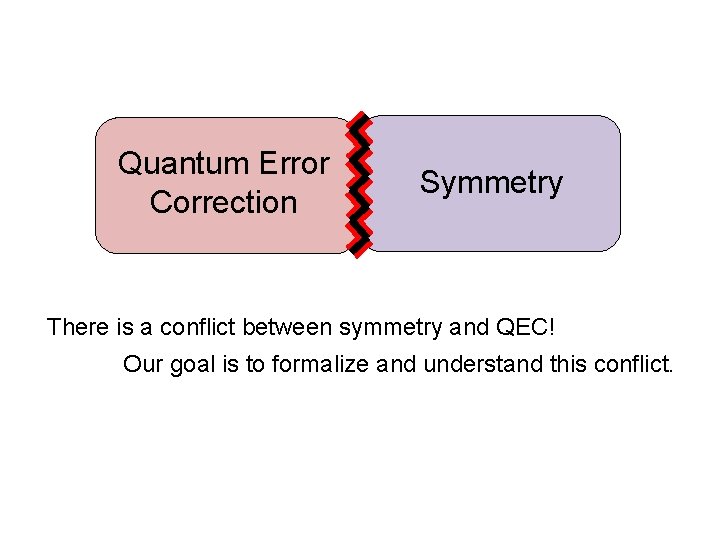
Quantum Error Correction Symmetry

Quantum Error Correction Symmetry There is a conflict between symmetry and QEC! Our goal is to formalize and understand this conflict.

Motivation and Definitions

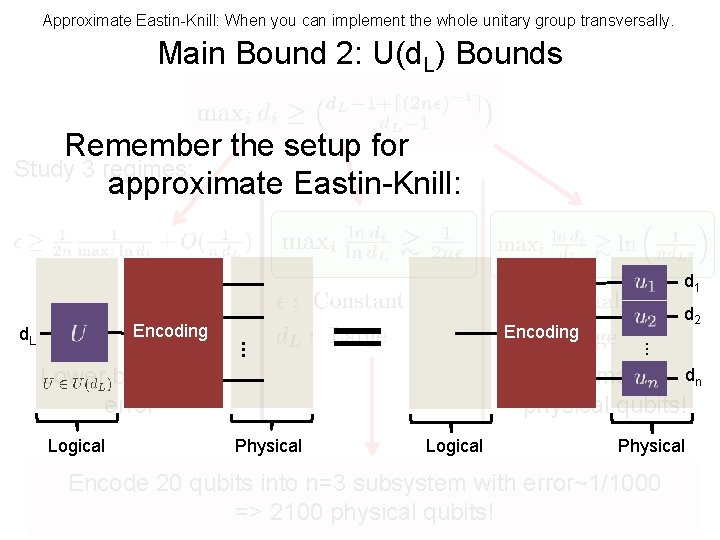
Quantum Error Correction: Encoding Logical Physical This talk: only erasure correction of a single physical subsystem!

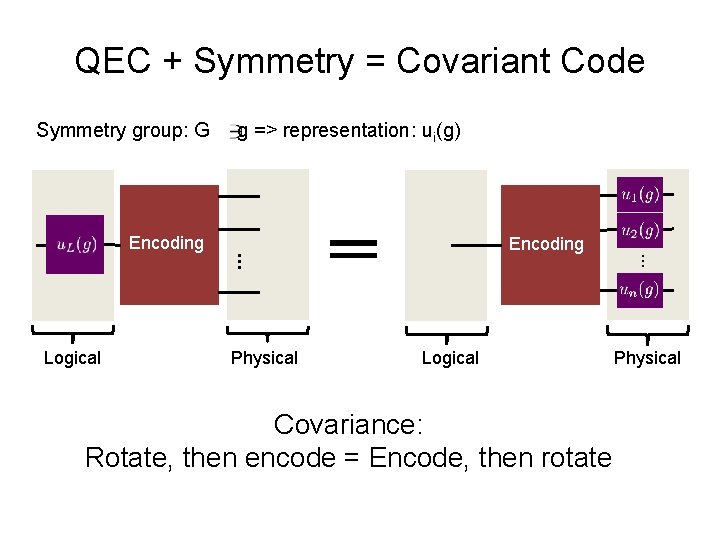
QEC + Symmetry = Covariant Code Symmetry group: G Physical Logical Covariance: Rotate, then encode = Encode, then rotate … Logical Encoding … Encoding g => representation: ui(g) Physical

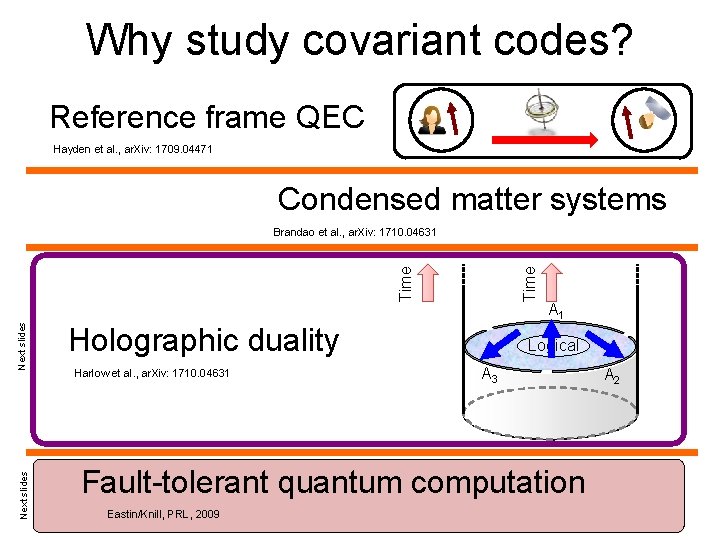
Why study covariant codes? Reference frame QEC Hayden et al. , ar. Xiv: 1709. 04471 Condensed matter systems Next slides Time Brandao et al. , ar. Xiv: 1710. 04631 Holographic duality Harlow et al. , ar. Xiv: 1710. 04631 A 1 Logical A 3 Fault-tolerant quantum computation Eastin/Knill, PRL, 2009 A 2

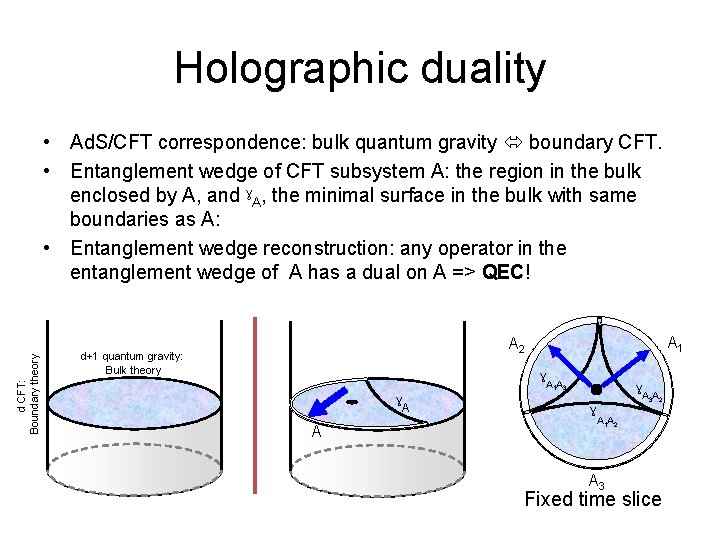
Holographic duality d CFT: Boundary theory • Ad. S/CFT correspondence: bulk quantum gravity boundary CFT. • Entanglement wedge of CFT subsystem A: the region in the bulk enclosed by A, and ˠA, the minimal surface in the bulk with same boundaries as A: • Entanglement wedge reconstruction: any operator in the entanglement wedge of A has a dual on A => QEC! A 1 A 2 d+1 quantum gravity: Bulk theory ˠA A 1 3 ˠA A 3 2 1 2 A 3 Fixed time slice

Holographic duality Time • Ad. S/CFT correspondence: bulk quantum gravity boundary CFT. • Entanglement wedge of CFT subsystem A: the region in the bulk enclosed by A, and ˠA, the minimal surface in the bulk with same boundaries as A: • Entanglement wedge reconstruction: any operator in the entanglement wedge of A has a dual on A => QEC! A 1 Symmetry: Time translation Logical A 3 A 2

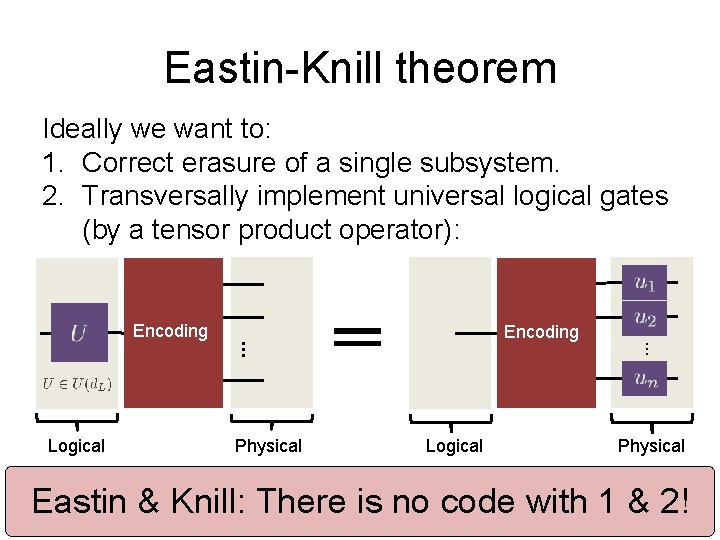
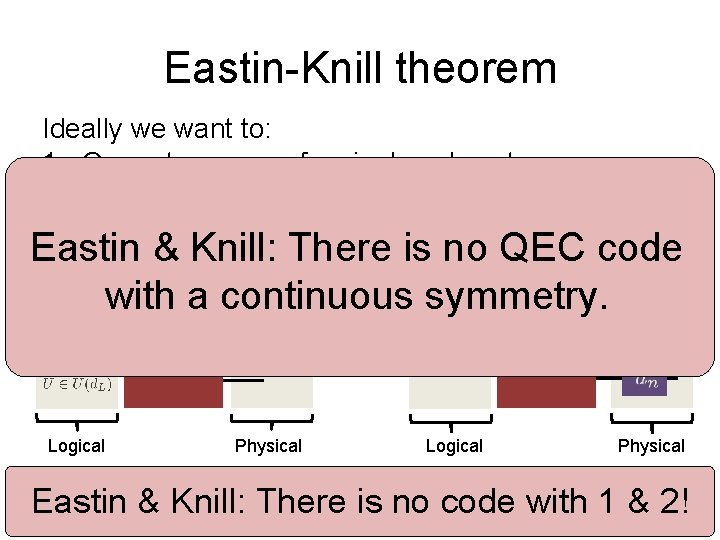
Eastin-Knill theorem Ideally we want to: 1. Correct erasure of a single subsystem. 2. Transversally implement universal logical gates (by a tensor product operator): Physical Logical … Logical Encoding … Encoding Physical Eastin & Knill: There is no code with 1 & 2!

Eastin-Knill theorem Ideally we want to: 1. Correct erasure of a single subsystem. 2. Transversally implement universal logical gates (by a tensor product operator): Eastin & Knill: There is no QEC code with a continuous symmetry. Physical Logical … Logical Encoding … Encoding Physical Eastin & Knill: There is no code with 1 & 2!

Eastin-Knill theorem ! s de Ideally we want to: o c t c 1. Correct erasure of a single subsystem. e f r e n p o 2. Transversally implement universal logical gates i d t e c e e r r (by a tensor productrioperator): o ly n c a r : Eastin & Knill: There is no QEC code s o y l s r l d i r e u e c n t e K S n m n u symmetry. i t oat continuous with t n n s a o ua Logical Physical Logical Encoding … … E d. Encoding q e e te mat W a m oxi i x o ppr r p p A A. . 2 1 Physical Eastin & Knill: There is no code with 1 & 2!

When do covariant codes exist? Quantum Error Correction Symmetry

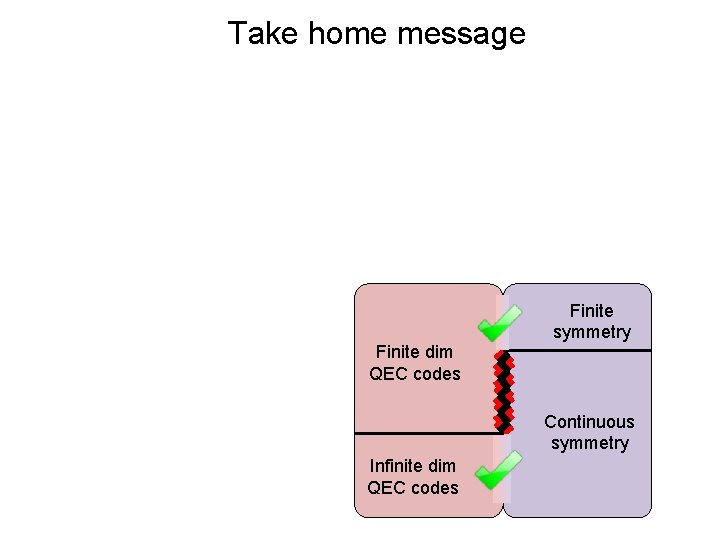
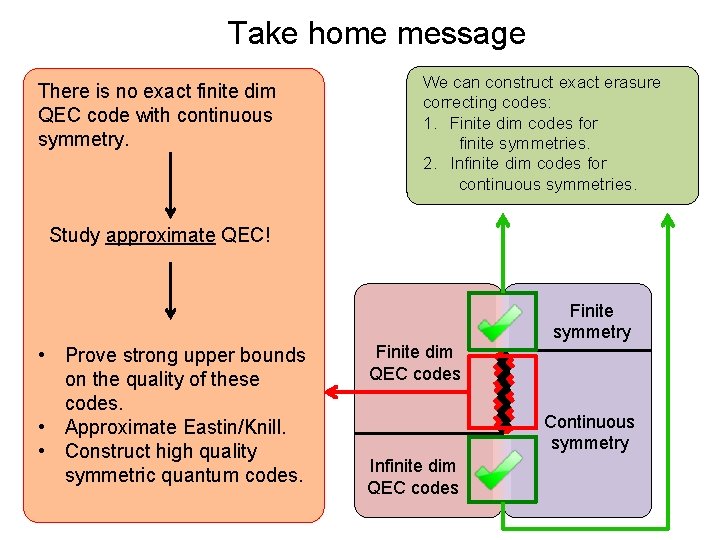
Take home message Finite dim QEC codes Finite symmetry Continuous symmetry Infinite dim QEC codes

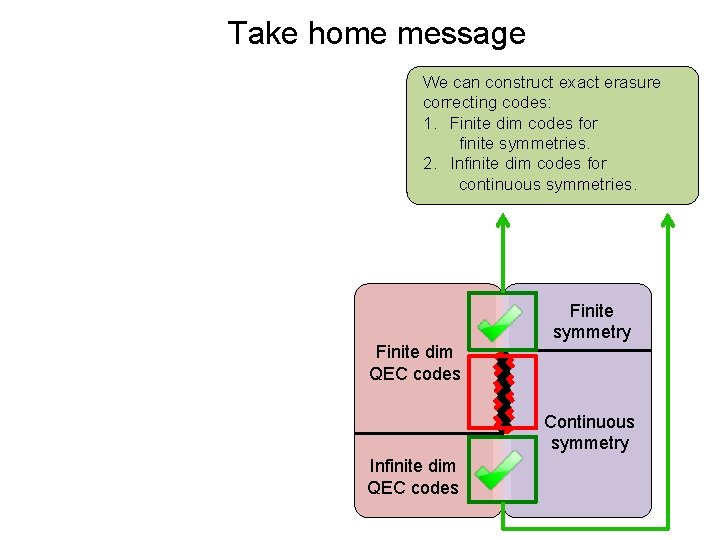
Take home message We can construct exact erasure correcting codes: 1. Finite dim codes for finite symmetries. 2. Infinite dim codes for continuous symmetries. Finite dim QEC codes Finite symmetry Continuous symmetry Infinite dim QEC codes

Take home message We can construct exact erasure correcting codes: 1. Finite dim codes for finite symmetries. 2. Infinite dim codes for continuous symmetries. We can construct codes on regular Finite symmetry Finite dim group. representation of any QEC codes Dimension of local subsystem = Continuous size of the symmetry group Infinite dim QEC codes Sometimes not normalizable…

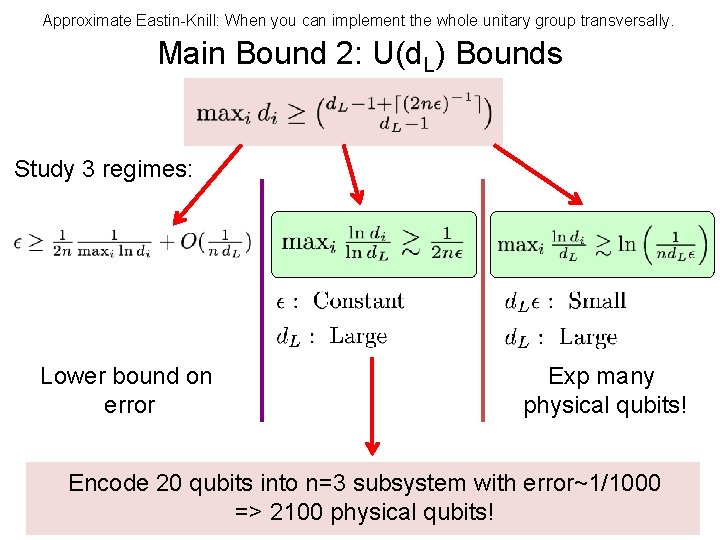
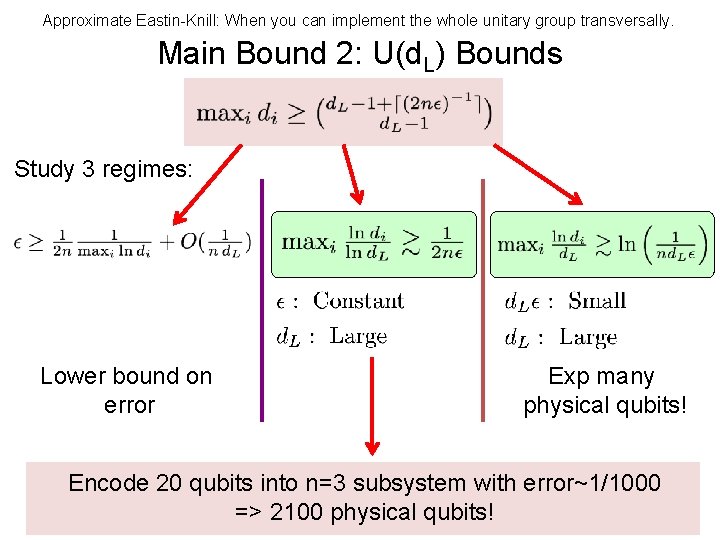
Take home message There is no exact finite dim QEC code with continuous symmetry. We can construct exact erasure correcting codes: 1. Finite dim codes for finite symmetries. 2. Infinite dim codes for continuous symmetries. Study approximate QEC! • Prove strong upper bounds on the quality of these codes. • Approximate Eastin/Knill. • Construct high quality symmetric quantum codes. Finite dim QEC codes Finite symmetry Continuous symmetry Infinite dim QEC codes

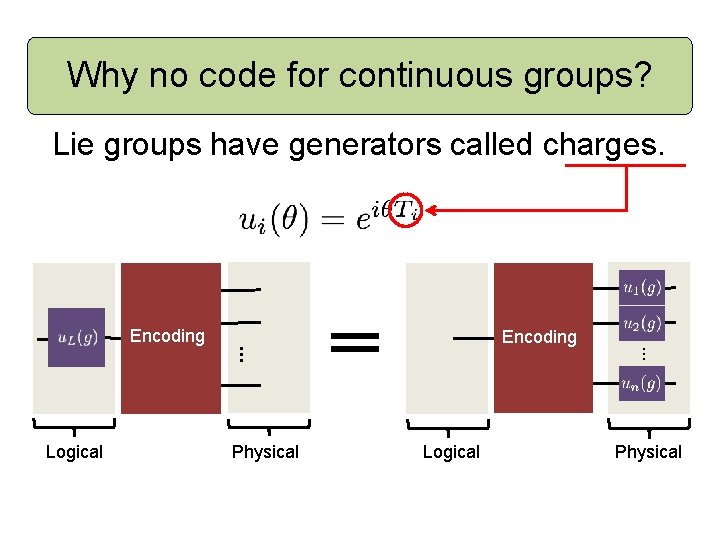
Why no code for continuous groups? Lie groups have generators called charges. Physical Logical … Logical Encoding … Encoding Physical

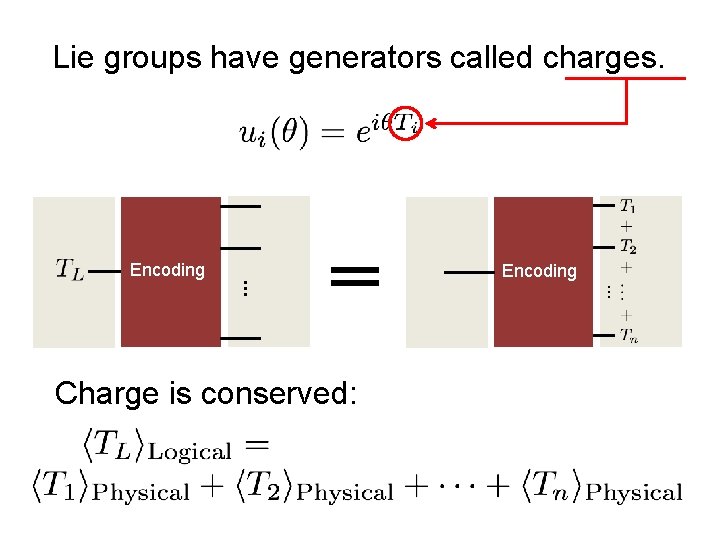
Lie groups have generators called charges. Charge is conserved: Encoding … … Encoding

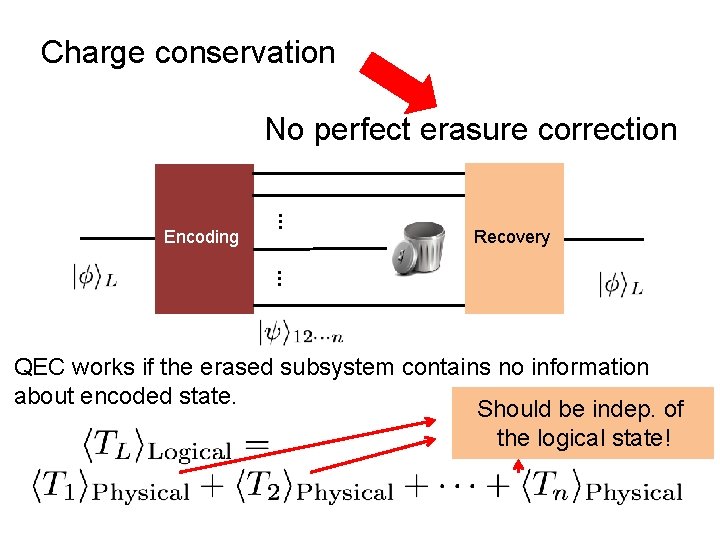
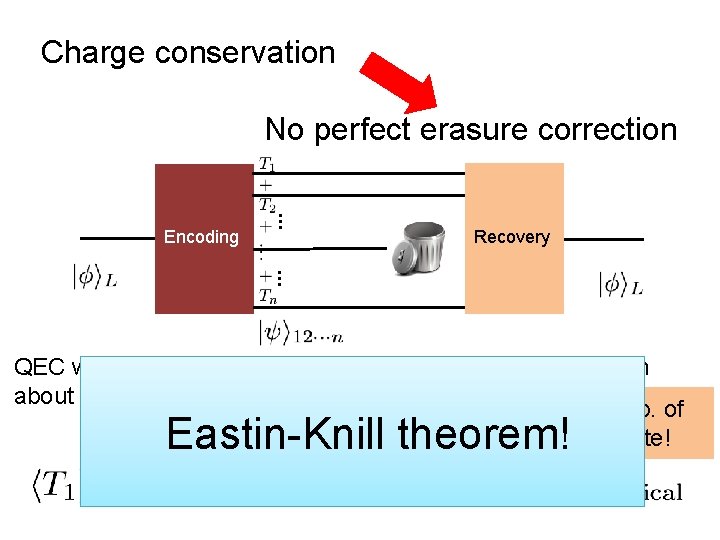
Charge conservation No perfect erasure correction … Encoding Recovery … QEC works if the erased subsystem contains no information about encoded state. Should be indep. of the logical state!

Charge conservation No perfect erasure correction … Encoding Recovery … QEC works if the erased subsystem contains no information about encoded state. Should be indep. of the logical state! Eastin-Knill theorem!

Study approximate QEC

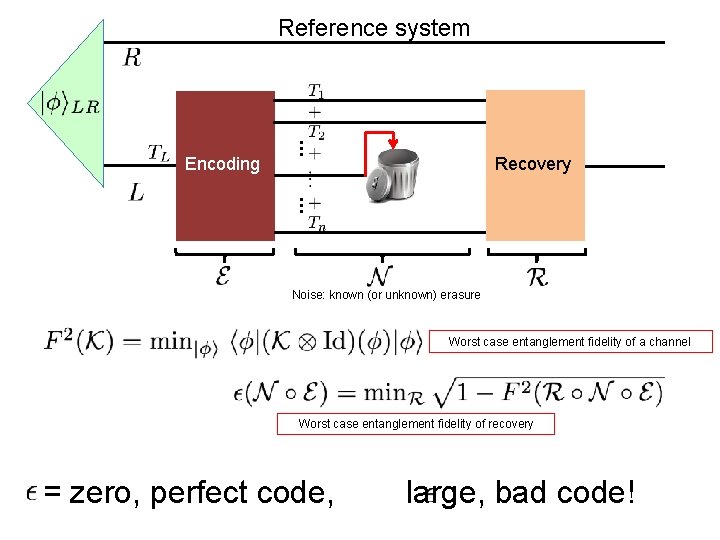
Reference system … Encoding Recovery … Noise: known (or unknown) erasure Worst case entanglement fidelity of a channel Worst case entanglement fidelity of recovery = zero, perfect code, large, bad code!

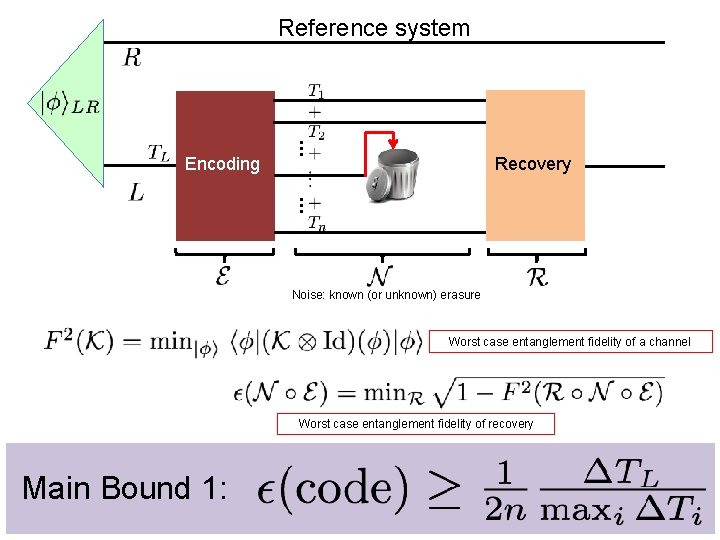
Reference system … Encoding Recovery … Noise: known (or unknown) erasure Worst case entanglement fidelity of a channel Worst case entanglement fidelity of recovery Main Bound 1:

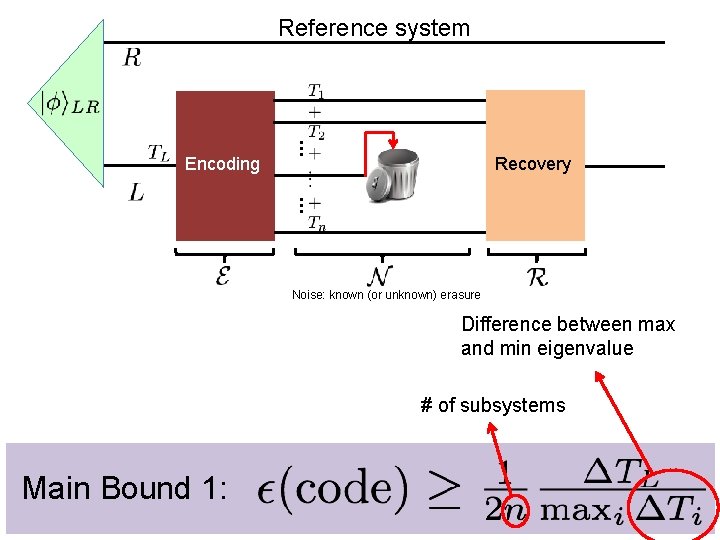
Reference system … Encoding Recovery … Noise: known (or unknown) erasure Difference between max and min eigenvalue # of subsystems Main Bound 1:

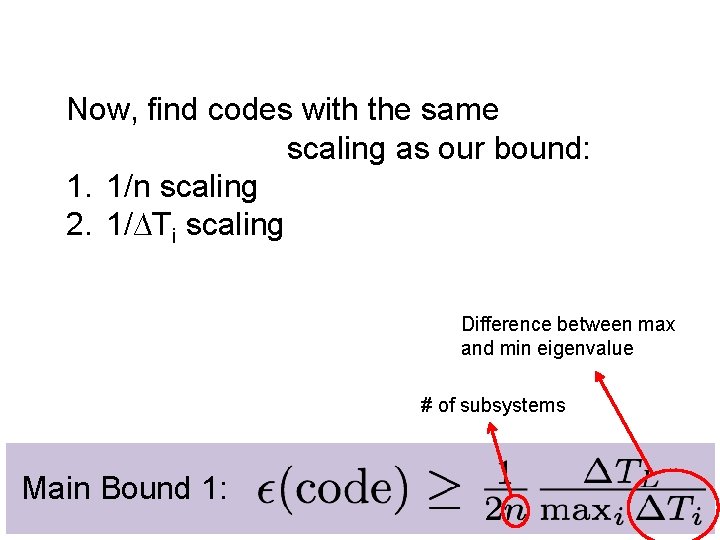
Now, find codes with the same scaling as our bound: 1. 1/n scaling 2. 1/∆Ti scaling Difference between max and min eigenvalue # of subsystems Main Bound 1:

Why large n helps ? There is less information about the charge in the erased subsystem! => Error scales as 1/n Brandao, et. al. Main Bound 1:

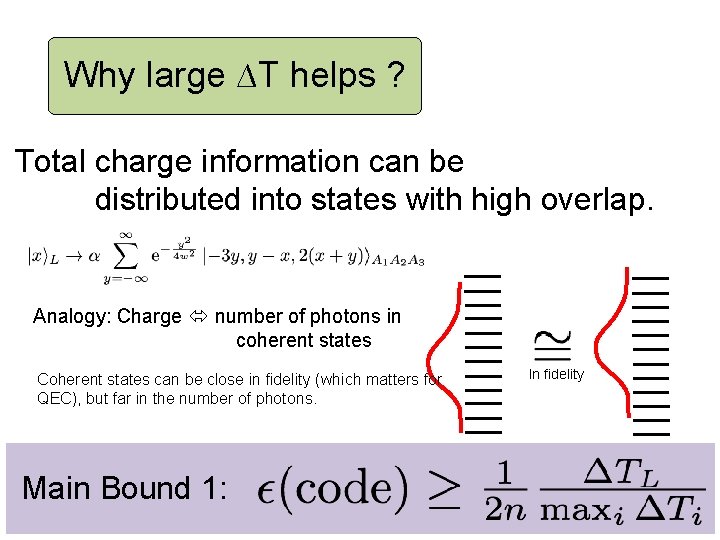
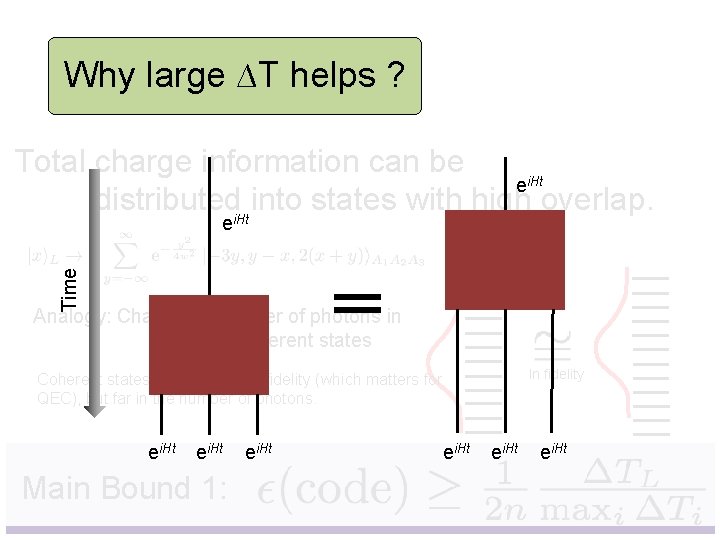
Why large ∆T helps ? Total charge information can be distributed into states with high overlap. Analogy: Charge number of photons in coherent states Coherent states can be close in fidelity (which matters for QEC), but far in the number of photons. Main Bound 1: In fidelity

Why large ∆T helps ? Total charge information can be ei. Ht distributedi. Ht into states with high overlap. Time e Analogy: Charge number of photons in coherent states In fidelity Coherent states can be close in fidelity (which matters for QEC), but far in the number of photons. ei. Ht Main Bound 1: ei. Ht

Non-Abelian groups give stronger bounds! in terms of dimension of subsystems, not norm of generators. Approximate Eastin-Knill theorem. Our bounds apply to non-abelian Lie groups, as they all have a U(1) subgroup. But we have not used the detailed representation theory of such groups.

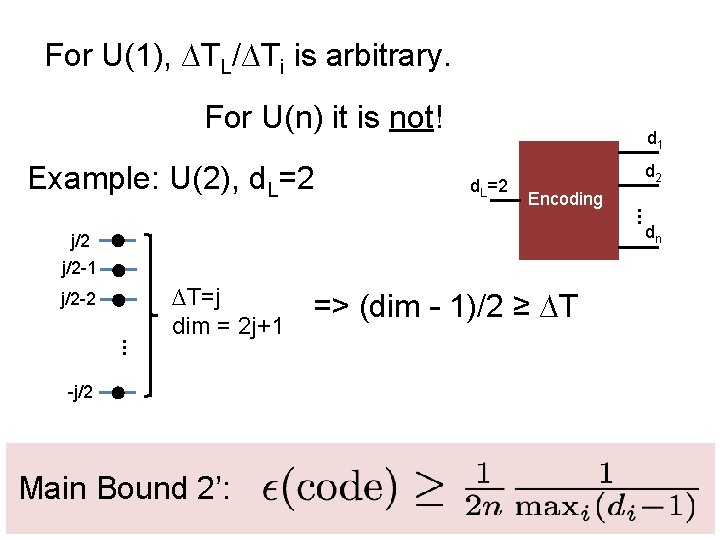
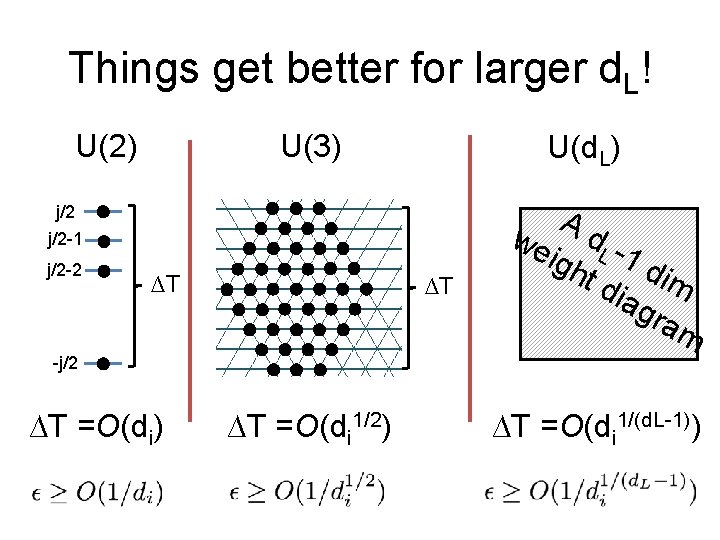
For U(1) covariant codes , ∆TL/∆Ti is free. For U(n) it is not! Example: U(2), d. L=2 j/2 -1 j/2 -2 … ∆T=j dim = 2 j+1 -j/2 Main Bound 1: => (dim – 1)/2 ≥ ∆T

For U(1), ∆TL/∆Ti is arbitrary. For U(n) it is not! Example: U(2), d. L=2 d 1 d. L=2 d 2 … Encoding dn j/2 -1 j/2 -2 … ∆T=j dim = 2 j+1 -j/2 Main Bound 2’: => (dim – 1)/2 ≥ ∆T

Things get better for larger d. L! U(2) U(3) U(d. L) j/2 -1 j/2 -2 ∆T ∆T Ad we igh L -1 d t d im iag ram -j/2 ∆T =O(di) ∆T =O(di 1/2) ∆T =O(di 1/(d. L-1))

Approximate Eastin-Knill: When you can implement the whole unitary group transversally. Main Bound 2: U(d. L) Bounds Study 3 regimes: Lower bound on error Exp many physical qubits! Encode 20 qubits into n=3 subsystem with error~1/1000 => 2100 physical qubits!

Approximate Eastin-Knill: When you can implement the whole unitary group transversally. Main Bound 2: U(d. L) Bounds Remember the setup for Study 3 regimes: approximate Eastin-Knill: d 1 Exp many dn physical qubits! Lower bound on error Logical … Encoding d. L d 2 Physical Logical Physical Encode 20 qubits into n=3 subsystem with error~1/1000 => 2100 physical qubits!

Approximate Eastin-Knill: When you can implement the whole unitary group transversally. Main Bound 2: U(d. L) Bounds Study 3 regimes: Lower bound on error Exp many physical qubits! Encode 20 qubits into n=3 subsystem with error~1/1000 => 2100 physical qubits!

Randomized Construction Encoding Choose the irreps , , and randomly, then choose a random isometry respecting the covariance. then: compare to our bound: for large di

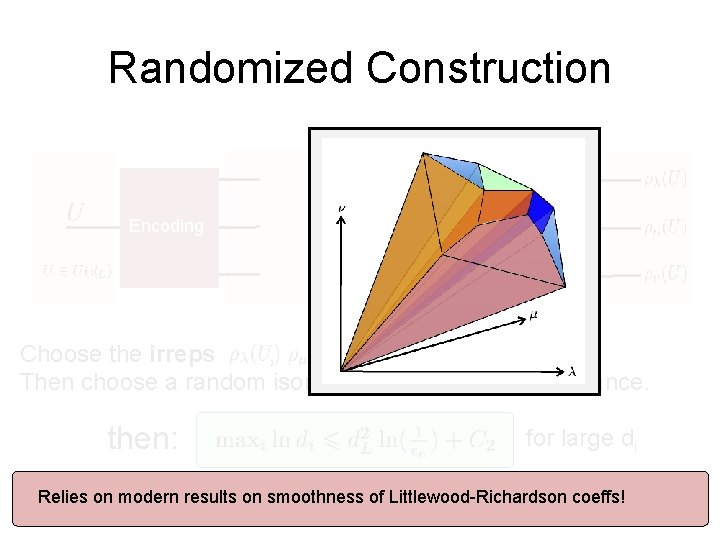
Randomized Construction Encoding Choose the irreps , , and randomly, Then choose a random isometry respecting the covariance. then: for large di Relies on modern results on smoothness of Littlewood-Richardson coeffs!

Discussion • • • We proved approximate versions on the Eastin-Knill theorem, discussed applications. We bound the recovery fidelity for approximate, covariant QEC. Stronger bounds for non-abelian groups. Constructions for codes covariant with the whole unitary group. Our bounds work for the overlapping generators (e. g. , local Hamiltonians), and approximate covariance. • Open questions and future directions: 1. De-randomize unitary covariant constructions. Can they be useful for fault-tolerance? 2. Strengthen the U(n) bounds. 3. How about other error models? photon loss?

Thank you!
 Quantum error correction
Quantum error correction Difference between error detection and error correction
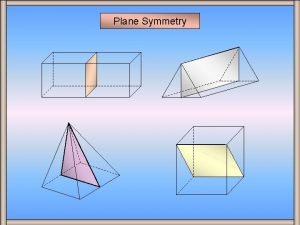
Difference between error detection and error correction Plane of symmetry for cuboid
Plane of symmetry for cuboid Generalized global symmetries
Generalized global symmetries Error detection in computer networks
Error detection in computer networks Error corection
Error corection Error detection and correction in data link layer
Error detection and correction in data link layer Concept of redundancy in error detection and correction
Concept of redundancy in error detection and correction 해밍코드 인코더
해밍코드 인코더 Edc error detection code
Edc error detection code Error detection and correction in computer networks
Error detection and correction in computer networks Crc in computer networks
Crc in computer networks Classical physics
Classical physics Quantum physics vs mechanics
Quantum physics vs mechanics Vec stata
Vec stata Eror
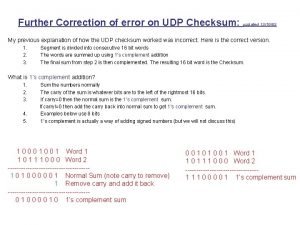
Eror Udp error correction
Udp error correction Wifi error correction
Wifi error correction Pecs error correction
Pecs error correction Good documentation practice
Good documentation practice Correction of error
Correction of error Correction of error
Correction of error Pcm
Pcm Good documentation practices in clinical research
Good documentation practices in clinical research Correction of prior period error
Correction of prior period error Hamming distance error detection
Hamming distance error detection Error correction model
Error correction model Error correction code
Error correction code Error correction model
Error correction model Two dimensional parity check
Two dimensional parity check Past continuous for future
Past continuous for future Present continuous past continuous future continuous
Present continuous past continuous future continuous Quantum error
Quantum error Type of errors in statistics
Type of errors in statistics Random and systematic errors examples
Random and systematic errors examples Round off error and truncation error
Round off error and truncation error Percentage uncertainty
Percentage uncertainty Type 1 error vs type 2 error example
Type 1 error vs type 2 error example Cdmvt aviation
Cdmvt aviation Example of hypothesis testing
Example of hypothesis testing Power swries
Power swries