Continuous Probability Distributions n The Uniform Distribution a

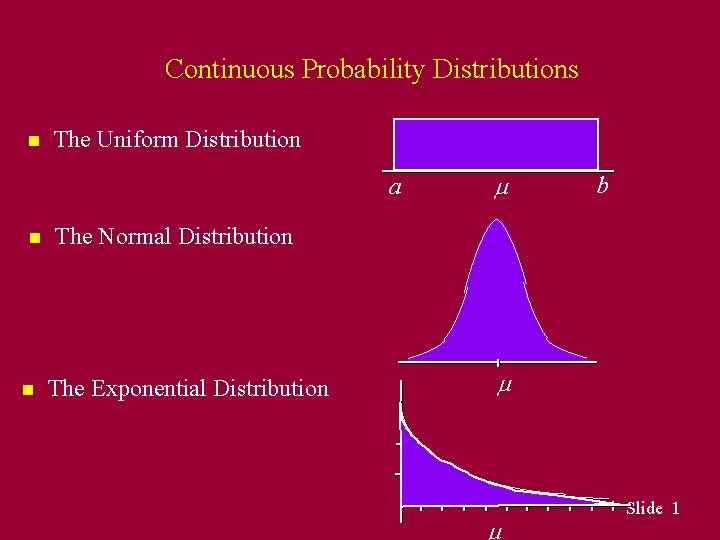
Continuous Probability Distributions n The Uniform Distribution a n n b The Normal Distribution The Exponential Distribution Slide 1

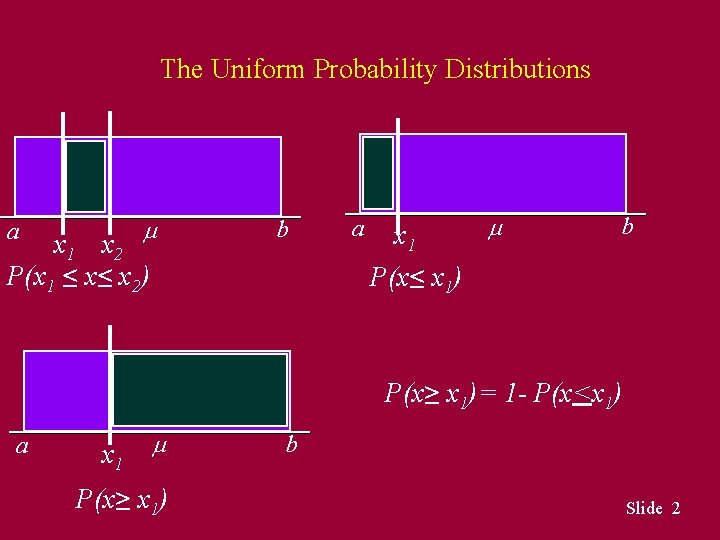
The Uniform Probability Distributions a x 1 x 2 P(x 1 ≤ x≤ x 2) b a x 1 P(x≤ x 1) b P(x≥ x 1)= 1 - P(x<x 1) a x 1 P(x≥ x 1) b Slide 2

The Uniform Probability Distribution Uniform Probability Density Function f (x) = 1/(b - a) for a < x < b = 0 elsewhere a = smallest value the variable can assume b = largest value the variable can assume n The probability of the continuous random variable assuming a specific value is 0. P(x=x 1) = 0 Slide 3

The Normal Probability Density Function where = mean = standard deviation = 3. 14159 e = 2. 71828 Slide 4

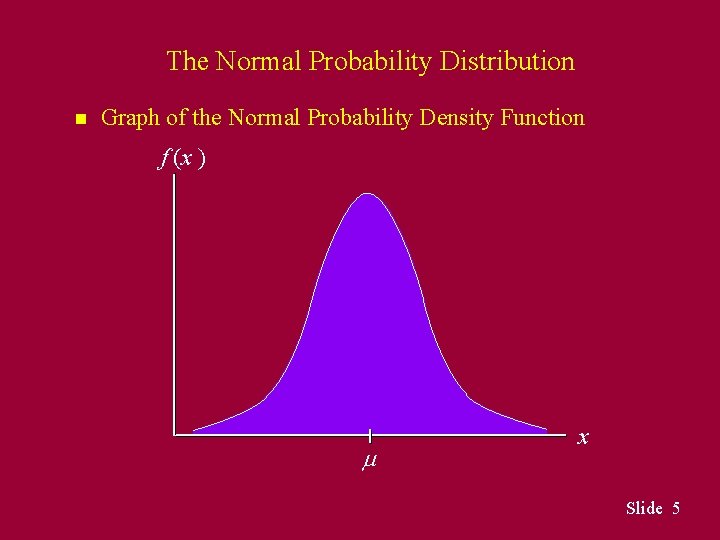
The Normal Probability Distribution n Graph of the Normal Probability Density Function f (x ) x Slide 5

The Standard Normal Probability Density Function where =0 =1 = 3. 14159 e = 2. 71828 Slide 6

Given any positive value for z, the table will give us the following probability The table will give this probability Given positive z The probability that we find using the table is the probability of having a standard normal variable between 0 and the given positive z. Slide 7

Given z =. 83 find the probability Slide 8

The Exponential Probability Distribution n Exponential Probability Density Function for x > 0, > 0 where n = mean e = 2. 71828 Cumulative Exponential Distribution Function where x 0 = some specific value of x Slide 9

Example The time between arrivals of cars at Al’s Carwash follows an exponential probability distribution with a mean time between arrivals of 3 minutes. Al would like to know the probability that the time between two successive arrivals will be 2 minutes or less. P(x < 2) = 1 - 2. 71828 -2/3 = 1 -. 5134 =. 4866 Slide 10

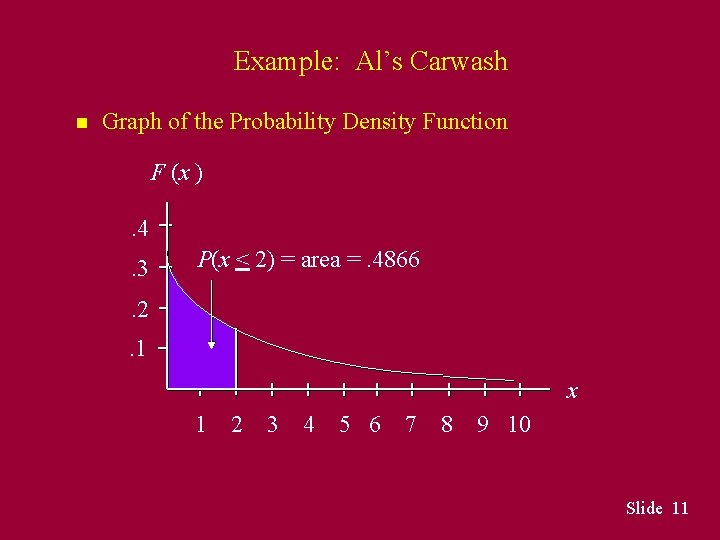
Example: Al’s Carwash n Graph of the Probability Density Function F (x ). 4. 3 P(x < 2) = area =. 4866 . 2. 1 x 1 2 3 4 5 6 7 8 9 10 Slide 11