Continuous Probability Distributions Continuous Random Variables and Probability

Continuous Probability Distributions

Continuous Random Variables and Probability Distributions • • Random Variable: Y Cumulative Distribution Function (CDF): F(y)=P(Y≤y) Probability Density Function (pdf): f(y)=d. F(y)/dy Rules governing continuous distributions: § f(y) ≥ 0 y § § P(a≤Y≤b) = F(b)-F(a) = § P(Y=a) = 0 a

Expected Values of Continuous RVs

Example – Cost/Benefit Analysis of Sprewell-Bluff Project (I) • Subjective Analysis of Annual Benefits/Costs of Project (U. S. Army Corps of Engineers assessments) • Y = Actual Benefit is Random Variable taken from a triangular distribution with 3 parameters: § A=Lower Bound (Pessimistic Outcome) § B=Peak (Most Likely Outcome) § C=Upper Bound (Optimistic Outcome) § 6 Benefit Variables § 3 Cost Variables Source: B. W. Taylor, R. M. North(1976). “The Measurement of Uncertainty in Public Water Resource Development, ” American Journal of Agricultural Economics, Vol. 58, #4, Pt. 1, pp. 636 -643
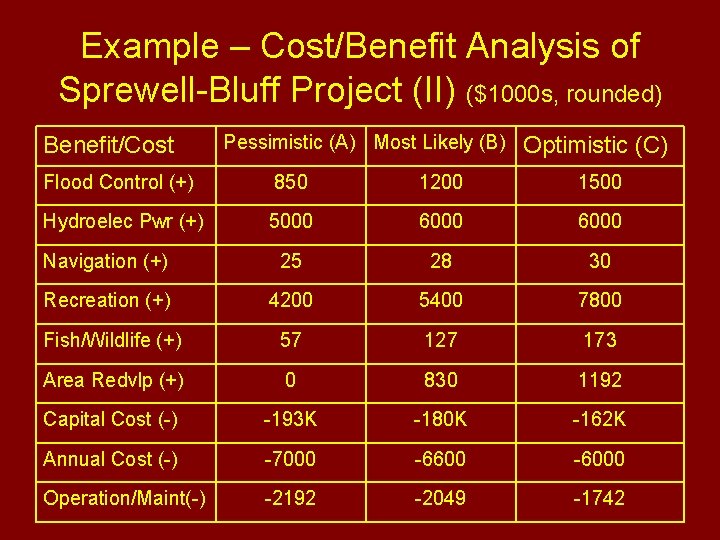
Example – Cost/Benefit Analysis of Sprewell-Bluff Project (II) ($1000 s, rounded) Benefit/Cost Pessimistic (A) Most Likely (B) Optimistic (C) Flood Control (+) 850 1200 1500 Hydroelec Pwr (+) 5000 6000 Navigation (+) 25 28 30 Recreation (+) 4200 5400 7800 Fish/Wildlife (+) 57 127 173 Area Redvlp (+) 0 830 1192 Capital Cost (-) -193 K -180 K -162 K Annual Cost (-) -7000 -6600 -6000 Operation/Maint(-) -2192 -2049 -1742
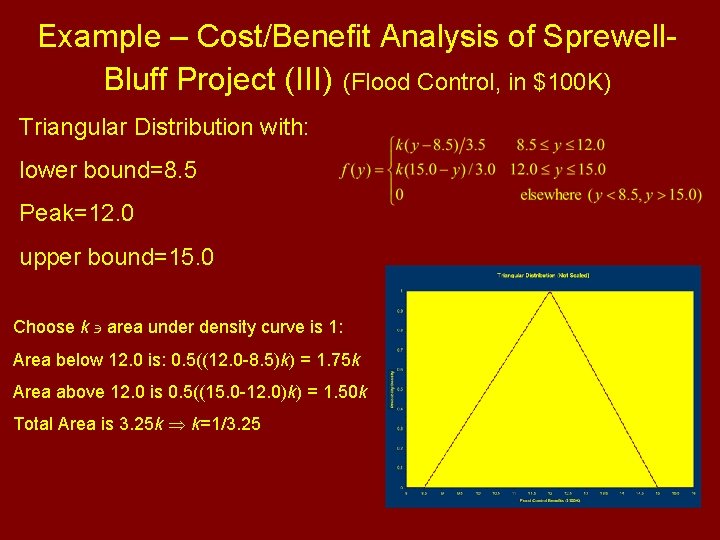
Example – Cost/Benefit Analysis of Sprewell. Bluff Project (III) (Flood Control, in $100 K) Triangular Distribution with: lower bound=8. 5 Peak=12. 0 upper bound=15. 0 Choose k area under density curve is 1: Area below 12. 0 is: 0. 5((12. 0 -8. 5)k) = 1. 75 k Area above 12. 0 is 0. 5((15. 0 -12. 0)k) = 1. 50 k Total Area is 3. 25 k k=1/3. 25

Example – Cost/Benefit Analysis of Sprewell -Bluff Project (IV) (Flood Control)

Example – Cost/Benefit Analysis of Sprewell -Bluff Project (V) (Flood Control)
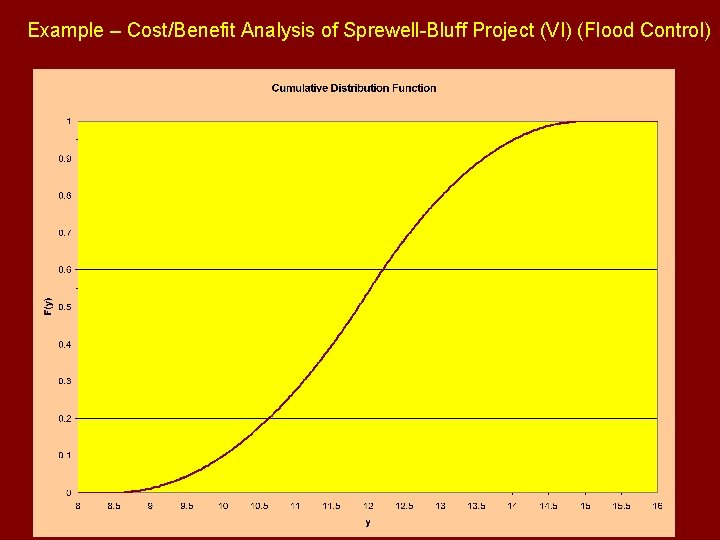
Example – Cost/Benefit Analysis of Sprewell-Bluff Project (VI) (Flood Control)

Example – Cost/Benefit Analysis of Sprewell-Bluff Project (VII) (Flood Control)

Uniform Distribution • Used to model random variables that tend to occur “evenly” over a range of values • Probability of any interval of values proportional to its width • Used to generate (simulate) random variables from virtually any distribution • Used as “non-informative prior” in many Bayesian analyses

Uniform Distribution - Expectations

Exponential Distribution • Right-Skewed distribution with maximum at y=0 • Random variable can only take on positive values • Used to model inter-arrival times/distances for a Poisson process
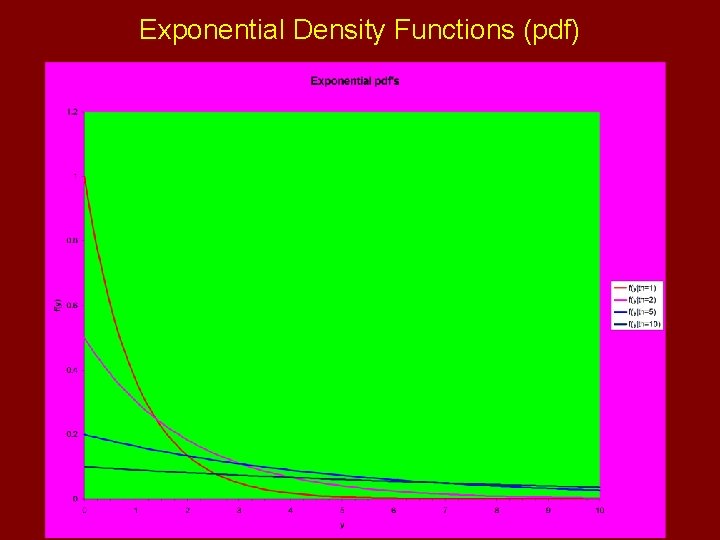
Exponential Density Functions (pdf)
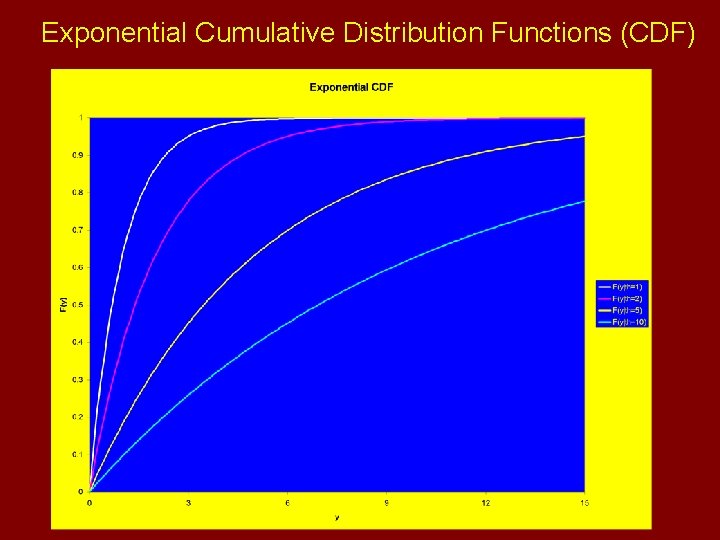
Exponential Cumulative Distribution Functions (CDF)

Gamma Function EXCEL Function: =EXP(GAMMALN(a))

Exponential Distribution - Expectations

Exponential Distribution - MGF

Exponential/Poisson Connection • Consider a Poisson process with random variable X being the number of occurences of an event in a fixed time/space X(t)~Poisson(lt) • Let Y be the distance in time/space between two such events • Then if Y > y, no events have occurred in the space of y

Gamma Distribution • • Family of Right-Skewed Distributions Random Variable can take on positive values only Used to model many biological and economic characteristics Can take on many different shapes to match empirical data Obtaining Probabilities in EXCEL: To obtain: F(y)=P(Y≤y) Use Function: =GAMMADIST(y, a, b, 1)
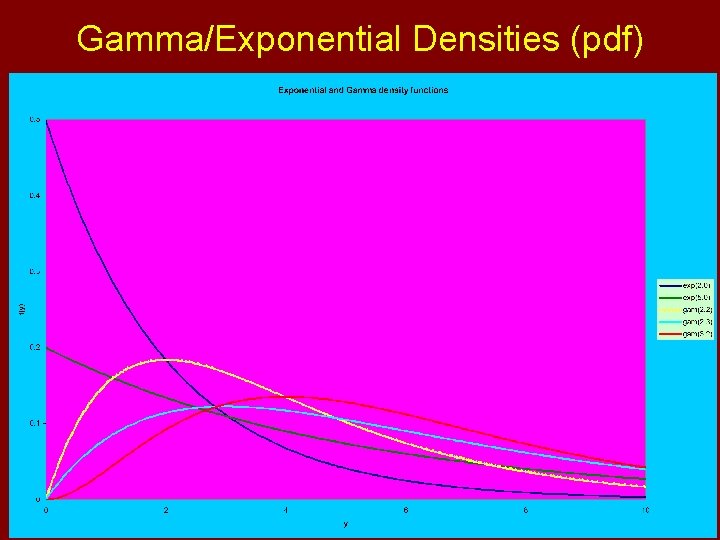
Gamma/Exponential Densities (pdf)

Gamma Distribution - Expectations

Gamma Distribution - MGF

Gamma Distribution – Special Cases • Exponential Distribution – a=1 • Chi-Square Distribution – a=n/2, b=2 (n ≡ integer) – – E(Y)=n V(Y)=2 n M(t)=(1 -2 t)-n/2 Distribution is widely used for statistical inference Notation: Chi-Square with n degrees of freedom:

Normal (Gaussian) Distribution • Bell-shaped distribution with tendency for individuals to clump around the group median/mean • Used to model many biological phenomena • Many estimators have approximate normal sampling distributions (see Central Limit Theorem) Obtaining Probabilities in EXCEL: To obtain: F(y)=P(Y≤y) Use Function: =NORMDIST(y, m, s, 1)
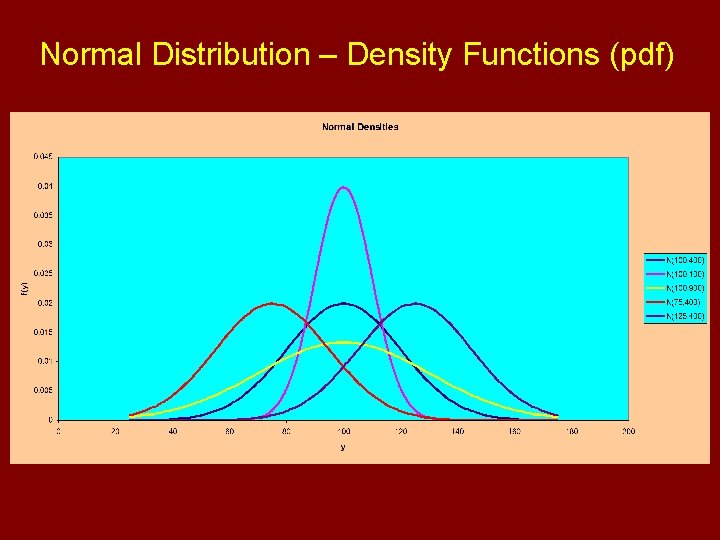
Normal Distribution – Density Functions (pdf)

Normal Distribution – Normalizing Constant

Obtaining Value of G(1/2)

Normal Distribution - Expectations

Normal Distribution - MGF

Normal(0, 1) – Distribution of Z 2

Beta Distribution • Used to model probabilities (can be generalized to any finite, positive range) • Parameters allow a wide range of shapes to model empirical data Obtaining Probabilities in EXCEL: To obtain: F(y)=P(Y≤y) Use Function: =BETADIST(y, a, b)
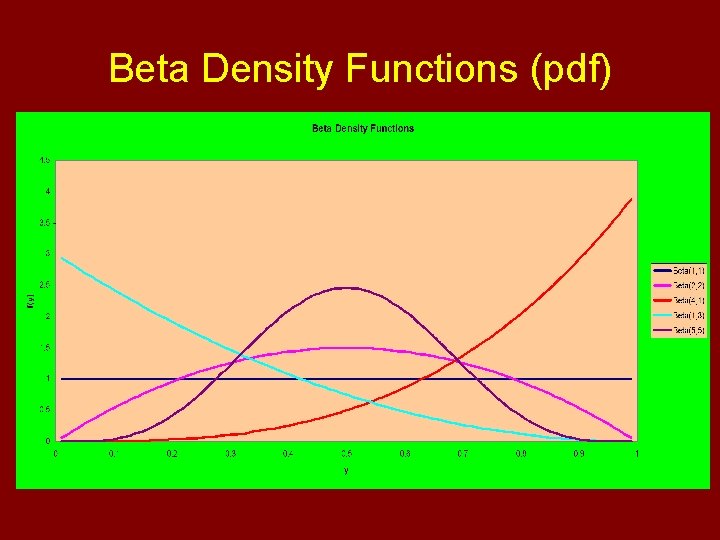
Beta Density Functions (pdf)

Weibull Distribution Note: The EXCEL function WEIBULL(y, a*, b*) uses parameterization: a*=b, b*=ab
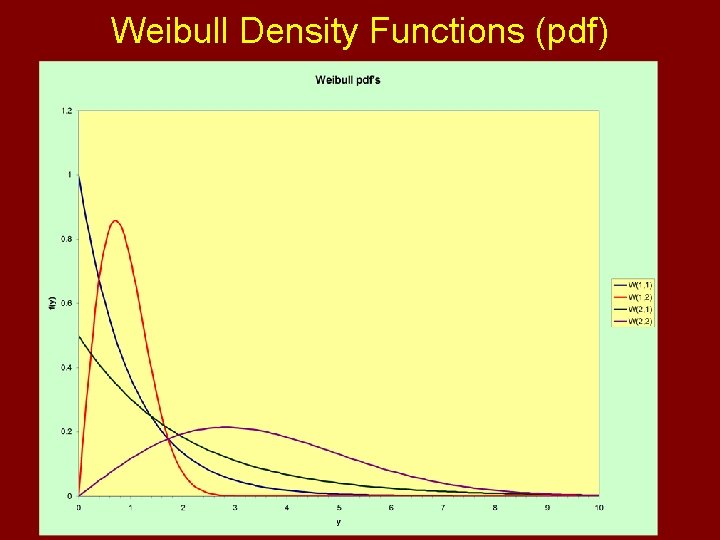
Weibull Density Functions (pdf)

Lognormal Distribution Obtaining Probabilities in EXCEL: To obtain: F(y)=P(Y≤y) Use Function: =LOGNORMDIST(y, m, s)
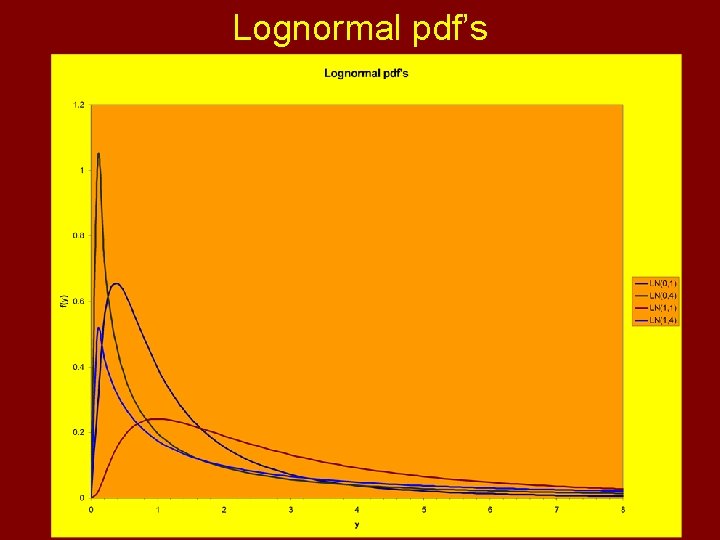
Lognormal pdf’s
- Slides: 37