Continuous Probability Distributions Continuous Probability Distribution Probability Density

第六章 連續機率分配 Continuous Probability Distributions

連續型機率分配 Continuous Probability Distribution 其函數稱 機率密度函數 Probability Density Function 機率值為 特定區間面積 條件

教材 6. 1 均勻(矩形)機率分配 Uniform Probability Distribution l Consider the random variable x representing the flight time of an airplane traveling from Chicago to New York. l Suppose the flight time can be any value in the interval from 120 minutes to 140 minutes. l Let us assume that sufficient actual flight data are available to conclude that the probability of a flight time with every 1 -minute interval being equally likely.

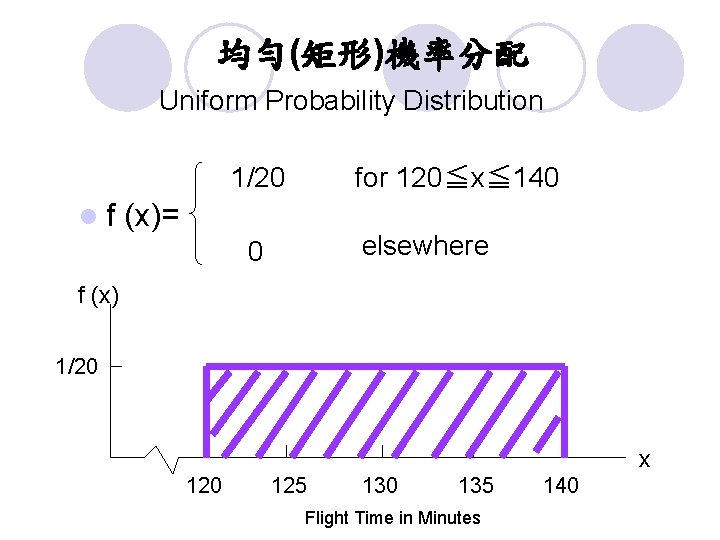
均勻(矩形)機率分配 Uniform Probability Distribution 1/20 lf for 120≦x≦ 140 (x)= elsewhere 0 f (x) 1/20 x 120 125 130 135 Flight Time in Minutes 140

均勻(矩形)機率分配 l 特性： 隨機變數在任何區間的機率皆相同 l Uniform Probability Density Function f (x)= 1 b-a for a ≦ x ≦ b (6. 1) 0 elsewhere

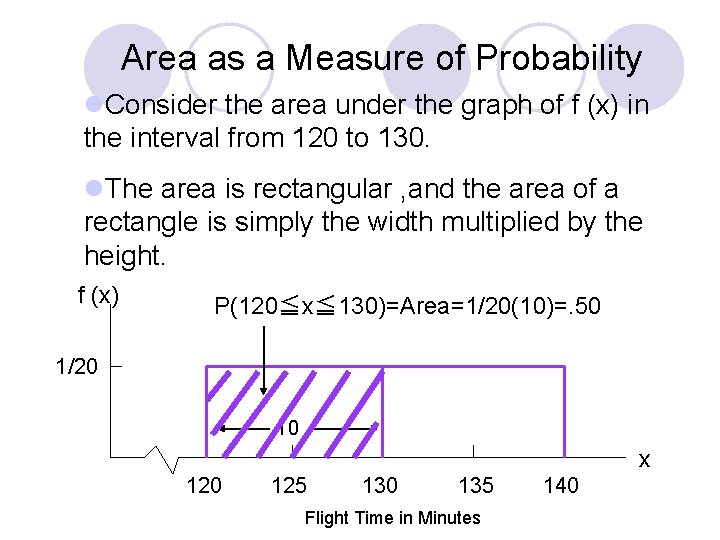
Area as a Measure of Probability l. Consider the area under the graph of f (x) in the interval from 120 to 130. l. The area is rectangular , and the area of a rectangle is simply the width multiplied by the height. f (x) P(120≦x≦ 130)=Area=1/20(10)=. 50 1/20 10 x 120 125 130 135 Flight Time in Minutes 140

l We talk about the probability of the random variable assuming a value within some given interval instead of a particular value. l The probability of the random variable assuming a value within some given interval from x 1 to x 2 is defined to be the area under the graph of the probability density function between x 1 and x 2. l The probability of a continuous random variable assuming any particular value exactly is zero.

The Expected Value and Variance of Uniform Continuous Probability 期望值 變異數 a is the smallest value and b is the largest value that the random variable may assume

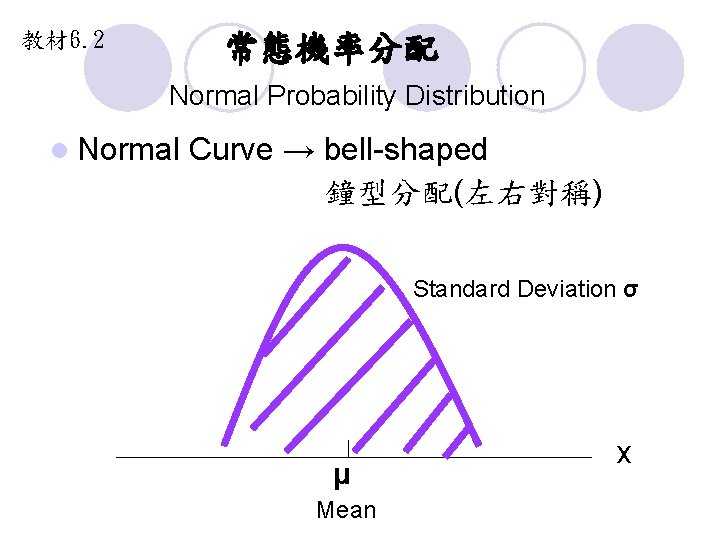
教材 6. 2 常態機率分配 Normal Probability Distribution l Normal Curve → bell-shaped 鐘型分配(左右對稱) Standard Deviation σ μ Mean x

Normal Probability Density Function (6. 2) where μ=mean σ=standard deviation π=3. 14159 e =2. 71828

The characteristics of the normal distribution 1. The entire family of normal distribution is differentiated by its mean μ and its standard deviation σ. 不同平均數及標準差形成不同常態分配 2. The highest point on the normal curve is at the mean , which is also the median and mode of the distribution. 最高點為平均數，平均數等於中位數等於眾數

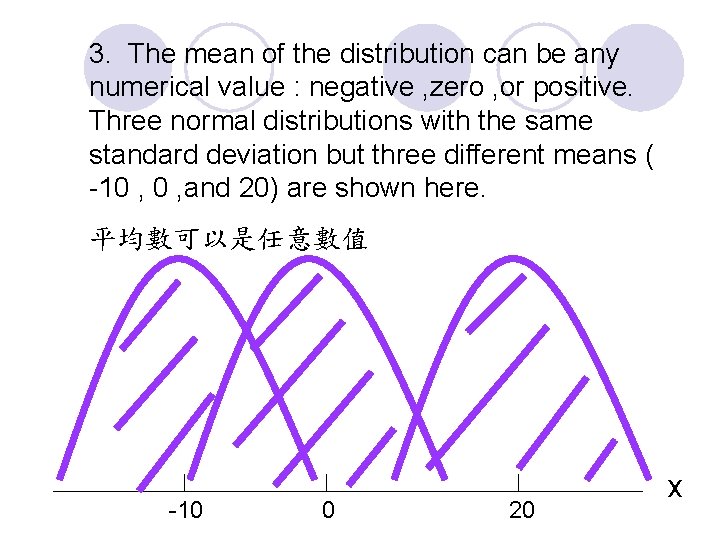
3. The mean of the distribution can be any numerical value : negative , zero , or positive. Three normal distributions with the same standard deviation but three different means ( -10 , and 20) are shown here. 平均數可以是任意數值 -10 0 20 x

4. The normal distribution is symmetric , with the shape of the curve to the left of the mean a mirror image of the shape of the curve to the right of the mean. The tail of the curve extend to infinity in both directions and theoretically never touch the horizontal axis. Because it is symmetric , the normal distribution is not skewed ; its skewness measure is zero. 是對稱分配，以平均數為對稱中心

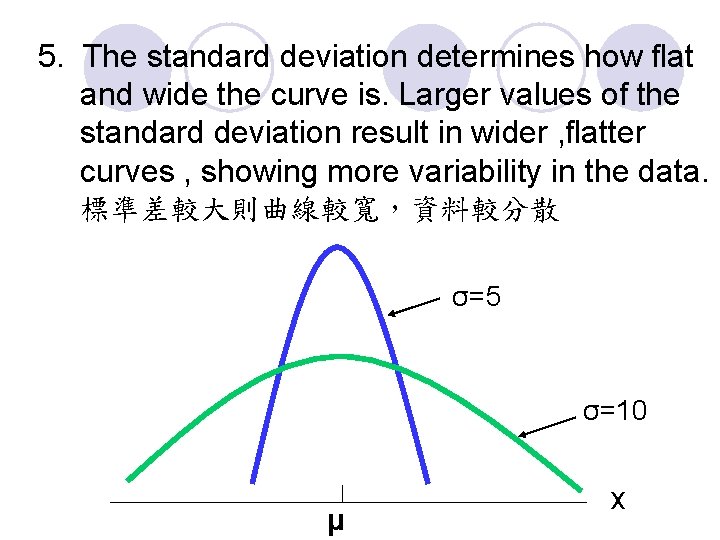
5. The standard deviation determines how flat and wide the curve is. Larger values of the standard deviation result in wider , flatter curves , showing more variability in the data. 標準差較大則曲線較寬，資料較分散 σ=5 σ=10 μ x

6. Probabilities for the normal random variable are given by areas under the curve. The total area under the curve for the normal distribution is 1. Because the distribution is symmetric , the area under the curve to the left of the mean is. 50 and the area under the curve to the right of the mean is. 50. 曲線下面積為 1

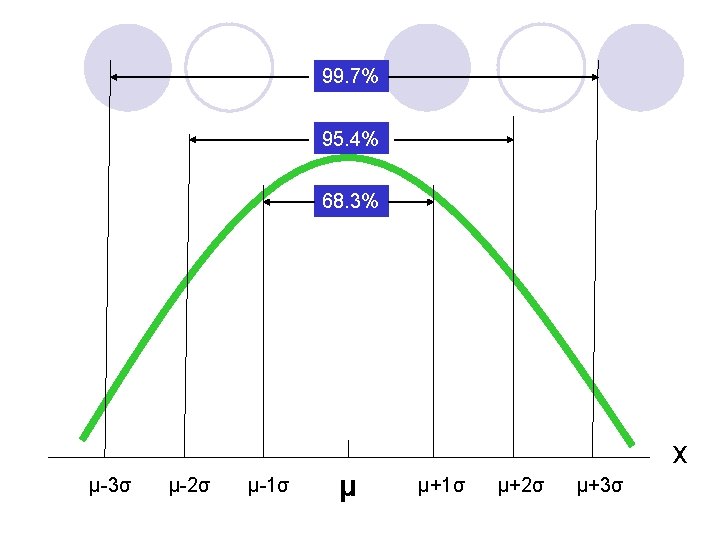
7. The percentage of values in some commonly used intervals are : (a) 68. 3% of the values of a normal random variable are within plus or minus one standard deviation of its mean. (b) 95. 4% of the values of a normal random variable are within plus or minus two standard deviation of its mean. (c) 99. 7% of the values of a normal random variable are within plus or minus three standard deviation of its mean.

Standard Normal Probability Distribution 標準常態分配 l A random variable that has a normal distribution with a mean of zero and a standard deviation of one is said to have a standard normal probability distribution. l The letter z is commonly used to designate this particular normal random variable. 轉換標準→ z = σ=1 X -μ σ x μ=0

Standard Normal Density function f (x) = 1 √ 2π e -z²/2

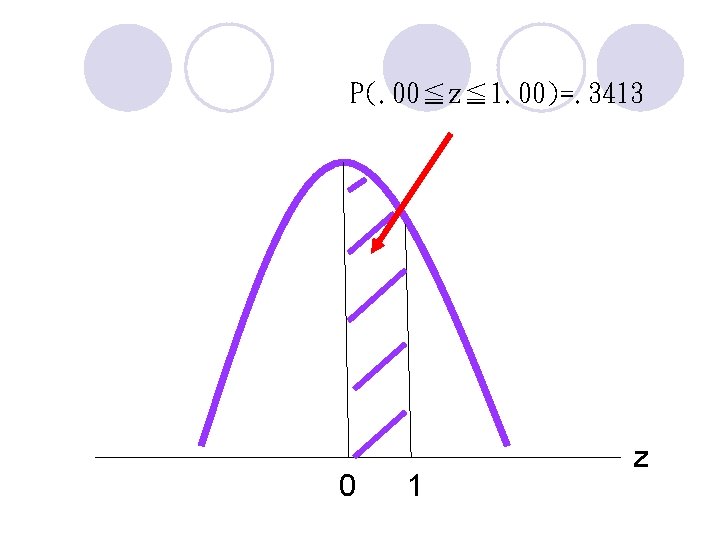
P(. 00≦z≦ 1. 00)=. 3413 0 1 z

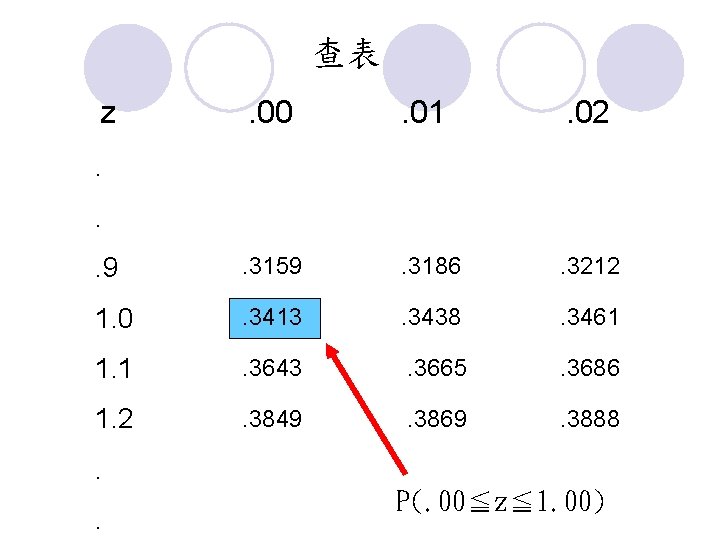
查表 z . 00 . 01 . 02 . 9 . 3159 . 3186 . 3212 1. 0 . 3413 . 3438 . 3461 1. 1 . 3643 . 3665 . 3686 1. 2 . 3849 . 3869 . 3888 . . P(. 00≦z≦ 1. 00)

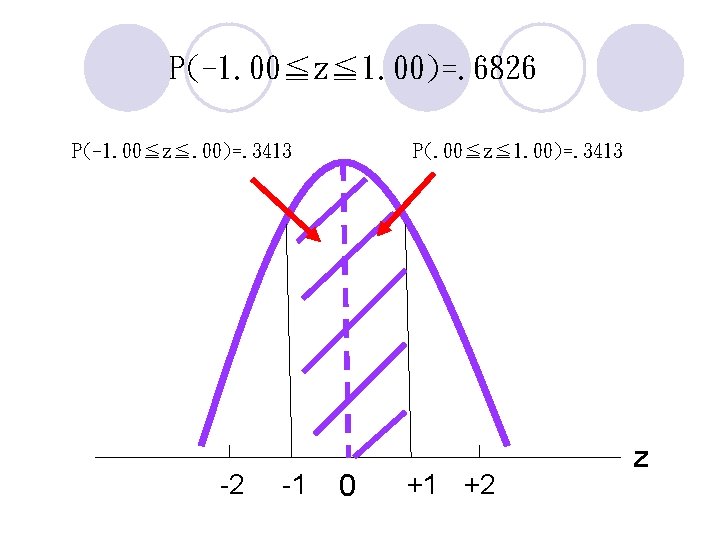
P(-1. 00≦z≦ 1. 00)=. 6826 P(-1. 00≦z≦. 00)=. 3413 -2 -1 P(. 00≦z≦ 1. 00)=. 3413 0 +1 +2 z

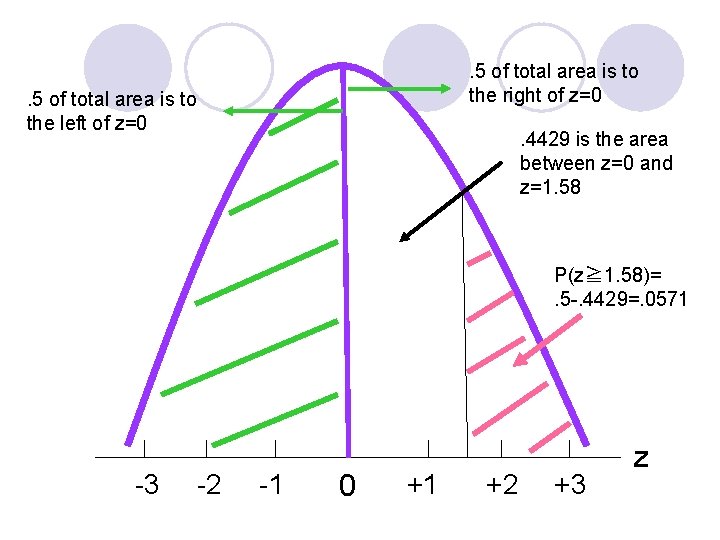
. 5 of total area is to the right of z=0 . 5 of total area is to the left of z=0 . 4429 is the area between z=0 and z=1. 58 P(z≧ 1. 58)=. 5 -. 4429=. 0571 -3 -2 -1 0 +1 +2 +3 z

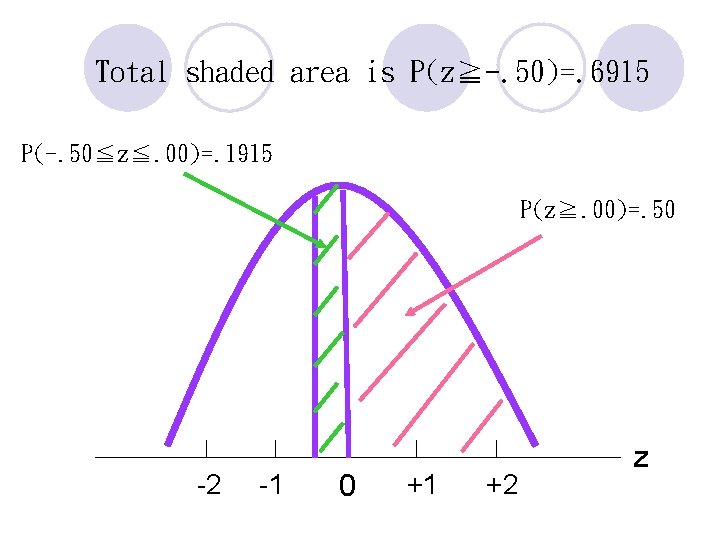
Total shaded area is P(z≧-. 50)=. 6915 P(-. 50≦z≦. 00)=. 1915 P(z≧. 00)=. 50 -2 -1 0 +1 +2 z

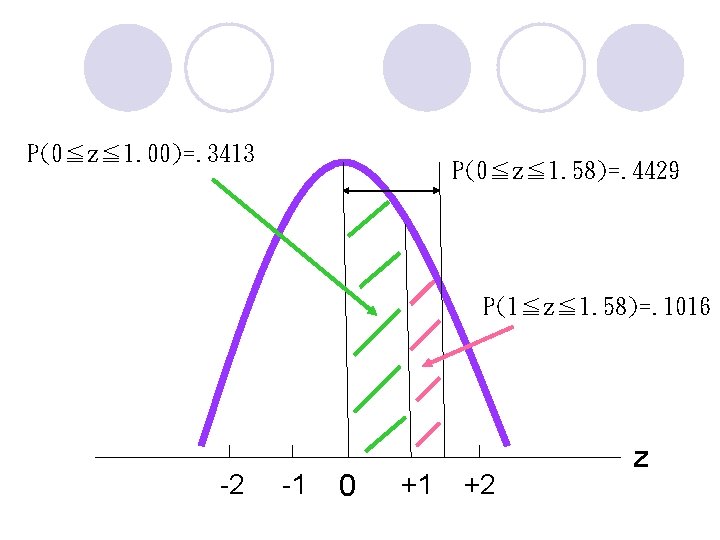
P(0≦z≦ 1. 00)=. 3413 P(0≦z≦ 1. 58)=. 4429 P(1≦z≦ 1. 58)=. 1016 -2 -1 0 +1 +2 z

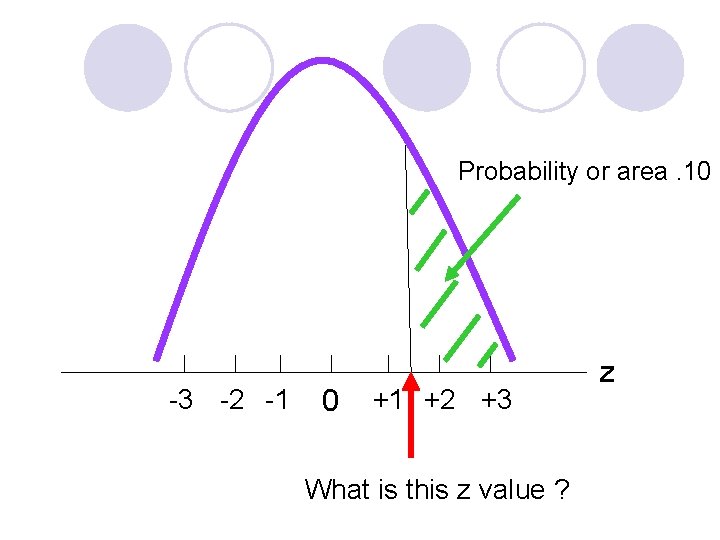
Probability or area. 10 -3 -2 -1 0 +1 +2 +3 What is this z value ? z

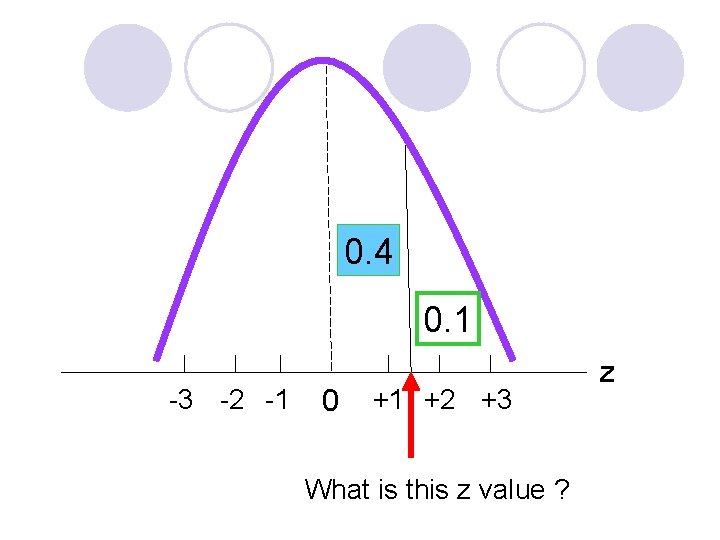
0. 4 0. 1 -3 -2 -1 0 +1 +2 +3 What is this z value ? z

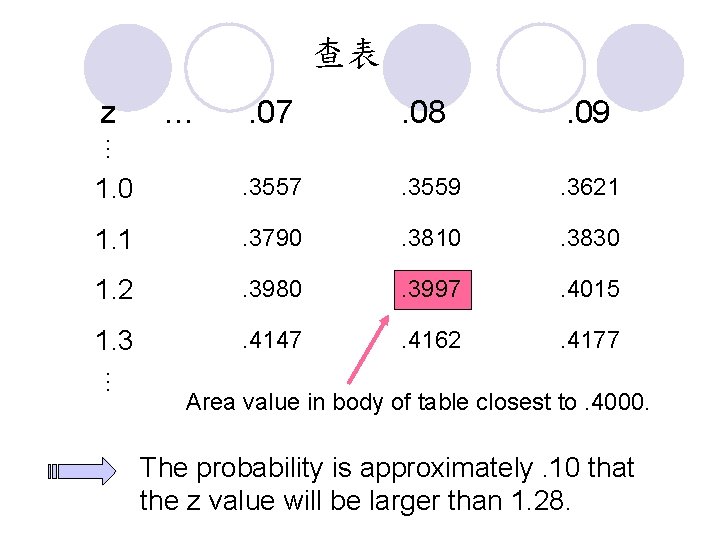
查表 z … . 08 . 09 1. 0 . 3557 . 3559 . 3621 1. 1 . 3790 . 3810 . 3830 1. 2 . 3980 . 3997 . 4015 1. 3 . 4147 . 4162 . 4177 … . 07 … Area value in body of table closest to. 4000. The probability is approximately. 10 that the z value will be larger than 1. 28.

Converting to the Standard Normal Distribution z= X -μ σ (6. 3) Example ： μ=10 σ=2 What is the probability that the random variable x is between 10 and 14 ?

Converting to the Standard Normal Distribution X = 10 Z = (10 -10)/2 = 0 X=14 Z = (14 -10)/2 = 2 →The probability of x being between 10 and 14 is given by the equivalent probability that z is between 0 and 2 for the standard normal distribution =. 4772.

Grear Tire Company Problem l Suppose the Grear Tire Company developed a new steel-belted radial tire , and managers believe that the mileage guarantee offered with the tire will be an important factor in the acceptance of the product. l The Grear`s managers want probability information about the number of miles the tires will last.

Grear Tire Company Problem l From actual road tests with the tires , Grear`s engineering group estimates： μ=36, 500 σ=5, 000 l The data collected indicate a normal distribution is a reasonable assumption. l What percentage of the tires can be expected to last more than 40, 000 miles? (What is the probability that the tire mileage will exceed 40, 000? )

Grear Tire Company Problem l At X=40, 000 , we have z = (x -μ) /σ = (40, 000 -36, 500)/5, 000 =. 70

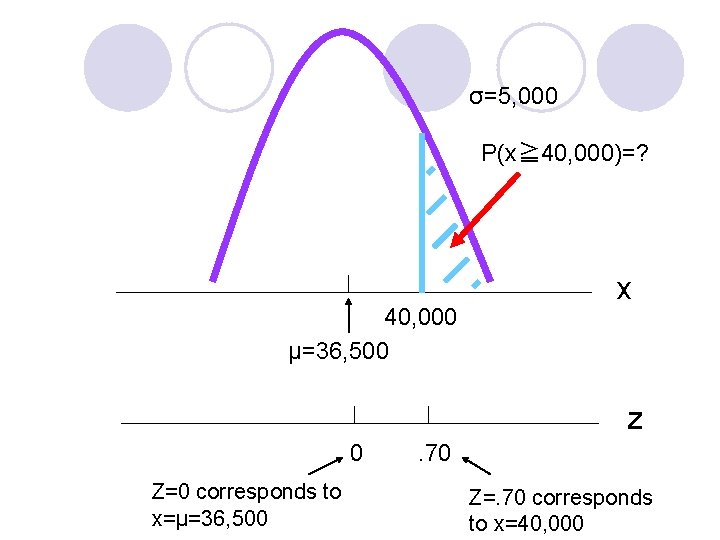
σ=5, 000 P(x≧ 40, 000)=? 40, 000 μ=36, 500 x z 0 Z=0 corresponds to x=μ=36, 500 . 70 Z=. 70 corresponds to x=40, 000

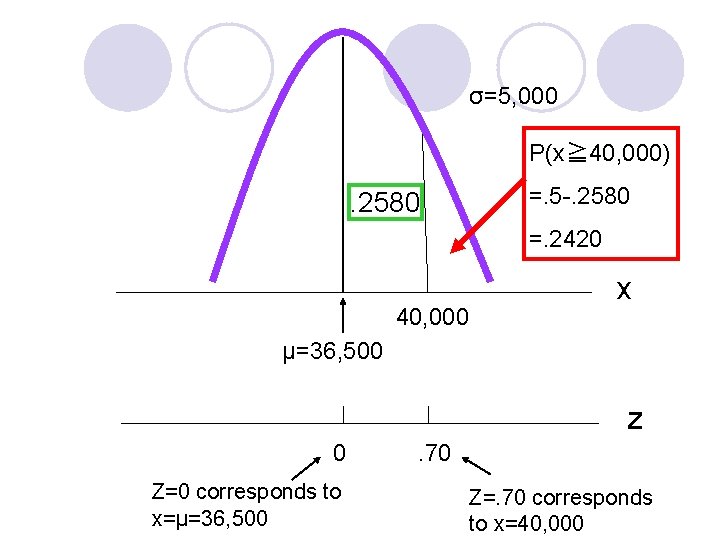
σ=5, 000 P(x≧ 40, 000) . 2580 =. 5 -. 2580 =. 2420 40, 000 x μ=36, 500 z 0 Z=0 corresponds to x=μ=36, 500 . 70 Z=. 70 corresponds to x=40, 000

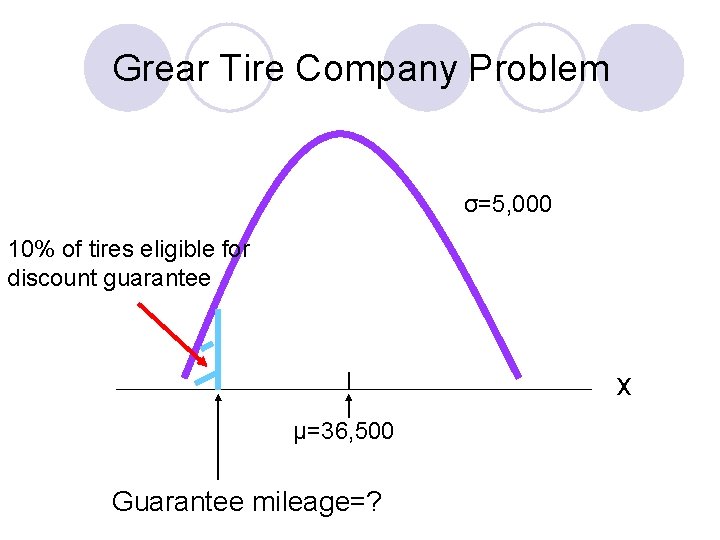
Grear Tire Company Problem σ=5, 000 10% of tires eligible for discount guarantee x μ=36, 500 Guarantee mileage=?

σ=5, 000 10% of tires eligible for discount guarantee 0. 4 x μ=36, 500 z 0 Z=-1. 28

Grear Tire Company Problem l To find the value of x corresponding to z=1. 28 , we have X -μ =-1. 28 → X =μ-1. 28σ z= σ With μ=36, 500 and σ=5, 000 X = 36, 500 - 1. 28(5, 000) = 30, 100 A guarantee of 30, 100 miles will meet the requirement that approximately 10% of the tires will be eligible for the guarantee.

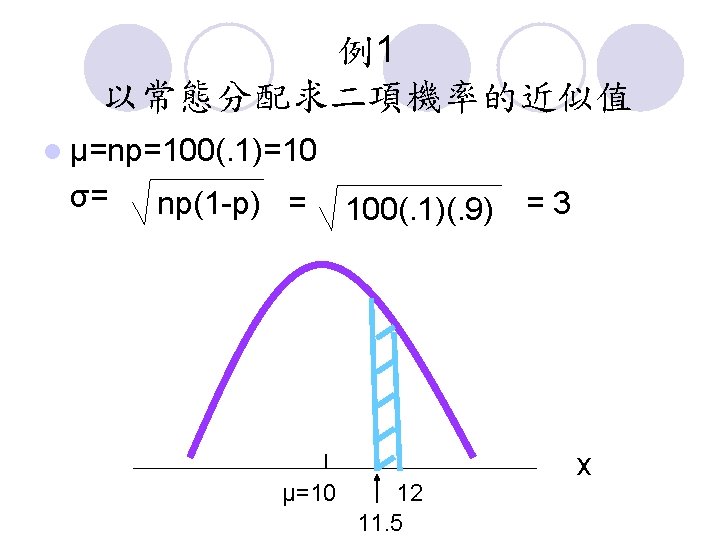
教材 6. 3 l In Normal Approximation of Binomial Probabilities case where the (1)number of trials is greater than 20 (2)np≥ 5 (3)n(1 -p) ≥ 5 , the normal distribution provides an easy-to-use approximation of binomial probabilities. l μ=np σ= np(1 -p)

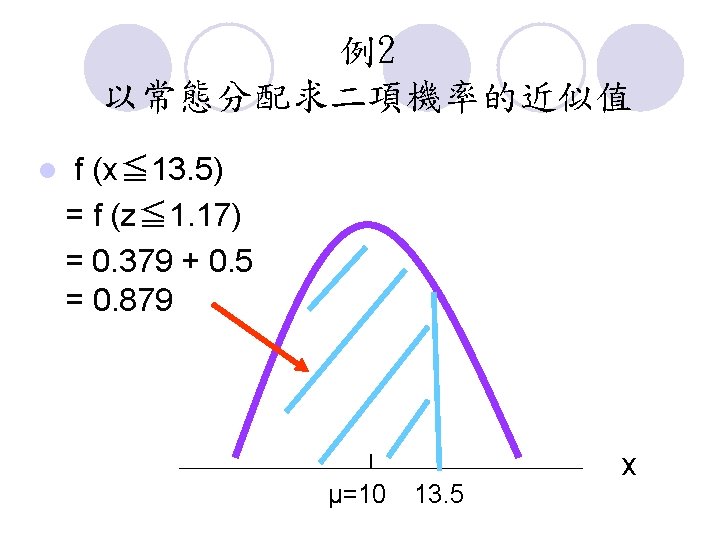
例1 以常態分配求二項機率的近似值 l Suppose a particular company has a history of making errors in 10% of its invoices. l. A sample of 100 invoices has been taken , and we want to compute the probability that 12 invoices contain errors. l That is , we want to find the binomial probability of 12 successes in 100 trials.

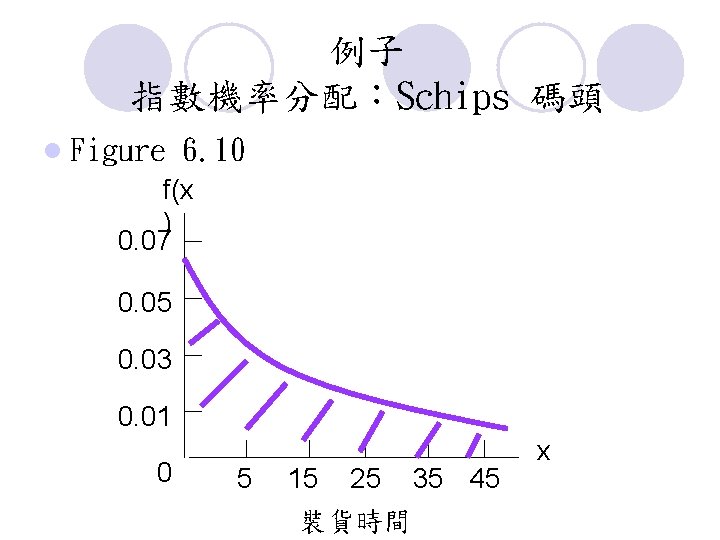
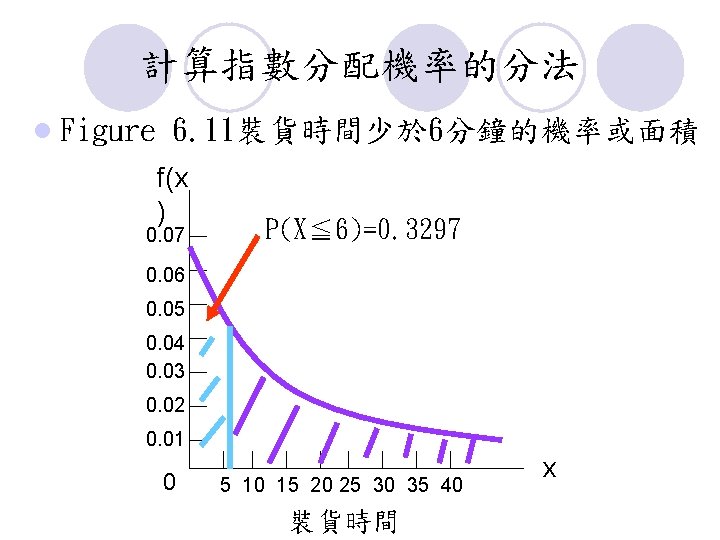
例子 指數機率分配：Schips 碼頭 l Figure 6. 10 f(x ) 0. 07 0. 05 0. 03 0. 01 0 5 15 25 35 45 裝貨時間 x