Continuous Probability Distributions A discrete random variable is

Continuous Probability Distributions A discrete random variable is a variable that can take on a countable number of possible values along a specified interval.

Continuous Probability Distributions A continuous random variable is a variable that can take on any of the possible values between two points.

Examples of Continuous Random variables 4 Time required to perform a job 4 Financial ratios 4 Product weights 4 Volume of soft drink in a 12 -ounce can 4 Interest rates 4 Income levels 4 Distance between two points

Continuous Probability Distributions The probability distribution of a continuous random variable is represented by a probability density function that defines a curve.

Continuous Probability Distributions (a) Discrete Probability Distribution P(X) (b) Probability Density Function f(X) x Possible Values of x

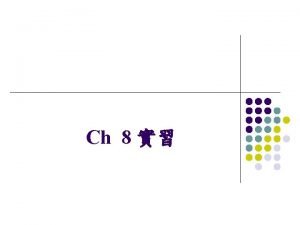
Normal Probability Distribution The Normal Distribution is a bell-shaped, continuous distribution with the following properties: 1. It is unimodal 2. It is symmetrical; symmetrical this means 50% of the area under the curve lies left of the center and 50% lies right of center. 3. The mean, median, and mode are equal. 4. It is asymptotic to the x-axis. 5. The amount of variation in the random variable determines the width of the normal distribution.

Normal Probability Distribution NORMAL DISTRIBUTION DENSITY FUNCTION where: x = Any value of the continuous random variable such that - < x < . = Population standard deviation e = Base of the natural log = 2. 7183 = Population mean

Normal Probability Distribution (Figure 5 -2) Probability = 0. 50 Mean Median Mode X

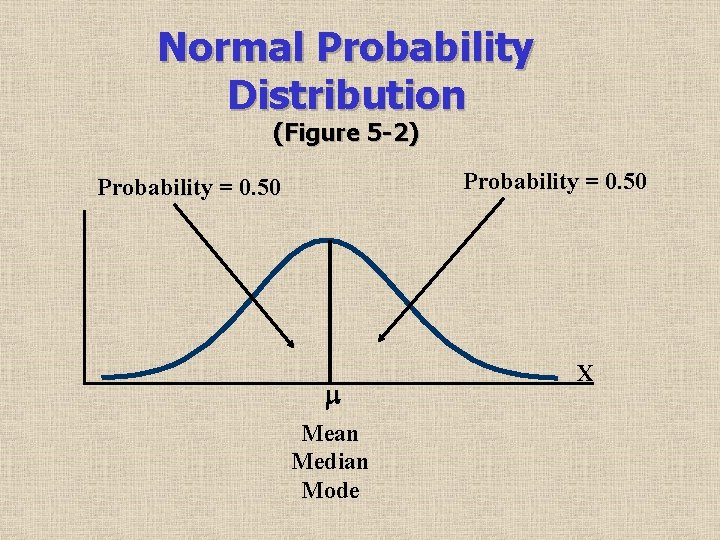
Difference Between Normal Distributions (Figure 5 -3) x (a) x (b) (c) x

Standard Normal Distribution The standard normal distribution is a normal distribution which has a mean = 0. 0 and a standard deviation = 1. 0. The horizontal axis is scaled in standardized z-values that measure the number of standard deviations a point is from the mean. Values above the mean have positive z-values and those below have negative zvalues.

Standard Normal Distribution STANDARDIZED NORMAL Z-VALUE where: x = Any point on the horizontal axis = Standard deviation of the normal distribution = Population mean z = Scaled value (the number of standard deviations a point x is from the mean)

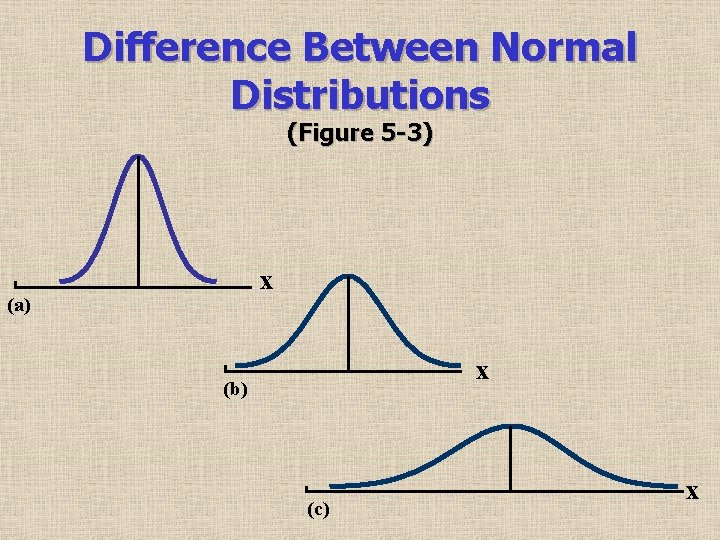
Areas Under the Standard Normal Curve (Using Table 5 -1) 0. 1985 0 0. 52 Example: z = 0. 52 (or -0. 52) A(z) = 0. 1985 or 19. 85% X

Areas Under the Standard Normal Curve (Table 5 -1)

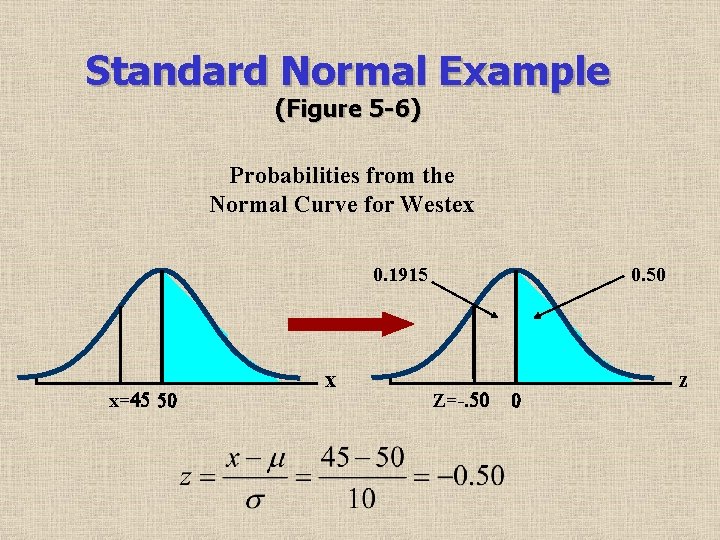
Standard Normal Example (Figure 5 -6) Probabilities from the Normal Curve for Westex 0. 1915 x=45 50 x 0. 50 Z=-. 50 0 z

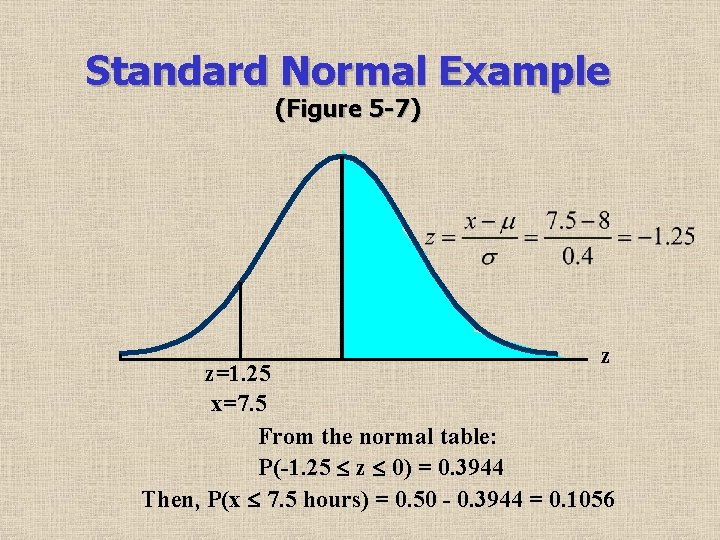
Standard Normal Example (Figure 5 -7) z z=1. 25 x=7. 5 From the normal table: P(-1. 25 z 0) = 0. 3944 Then, P(x 7. 5 hours) = 0. 50 - 0. 3944 = 0. 1056