Continuous Probability Distributions 1 Common Probability distributions Normal

Continuous Probability Distributions ﺗﻮﺍﺑﻊ ﺗﻮﺯیﻊ پیﻮﺳﺘﻪ 1

Common Probability distributions ﺗﻮﺯیﻊ ﻫﺎی ﺍﺣﺘﻤﺎﻝ • Normal family ﺧﺎﻧﻮﺍﺩﻩ ﻧﺮﻣﺎﻝ – Normal, lognormal-III • Generalized Extreme Value family ﺧﺎﻧﻮﺍﺩﻩ ﻣﻘﺎﺩیﺮ ﺣﺪی (EV 1 (Gumbel), GEV II, and EVIII (Weibull)) • Pearson type family ﺧﺎﻧﻮﺍﺩﻩ پیﺮﺳﻮﻥ – Gamma, Exponential, Pearson type III, Log. Pearson type III 2

Common Probability distributions ﺗﻮﺯیﻊ ﻫﺎی ﺍﺣﺘﻤﺎﻝ • Normal family ﺧﺎﻧﻮﺍﺩﻩ ﻧﺮﻣﺎﻝ – Normal, lognormal-III • Generalized Extreme Value family ﺧﺎﻧﻮﺍﺩﻩ ﻣﻘﺎﺩیﺮ ﺣﺪی (EV 1 (Gumbel), GEV II, and EVIII (Weibull)) • Pearson type family ﺧﺎﻧﻮﺍﺩﻩ پیﺮﺳﻮﻥ – Gamma, Exponential, Pearson type III, Log. Pearson type III 3

Normal Random Variable • A normally distributed random variable, is a random variable that has a relative frequency histogram in the shape of a normal (Gaussian) curve. • The normal distribution models bell shaped frequency distributions • The normal distribution is the fundamental distribution underlying most of inferential statistics 8. 4

The Normal Distribution… Important things to note: • The normal distribution is fully defined by two parameters: its standard deviation and mean • The normal distribution is bell shaped and symmetrical about the mean • Normal distributions range from minus infinity to plus infinity 8. 5

The Normal Distribution: This is a bell shaped Note constants: curve with different =3. 14159 centers and spreads e=2. 71828 on and depending 8. 6
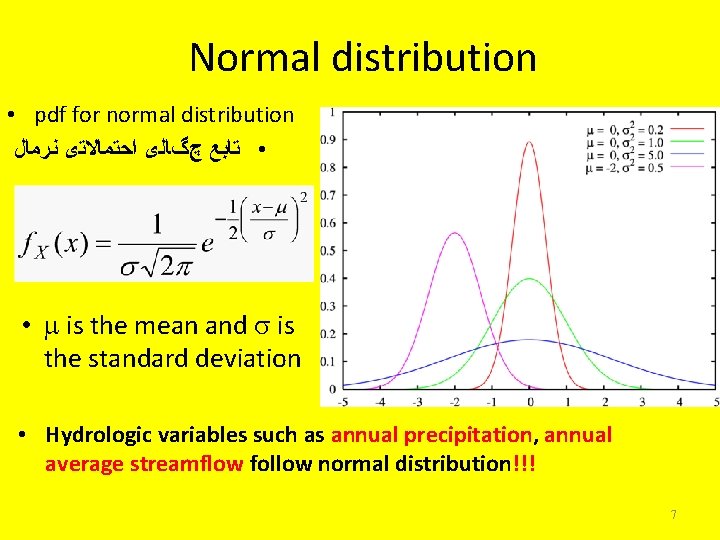
Normal distribution • pdf for normal distribution • ﺗﺎﺑﻊ چگﺎﻟی ﺍﺣﺘﻤﺎﻻﺗی ﻧﺮﻣﺎﻝ • is the mean and is the standard deviation • Hydrologic variables such as annual precipitation, annual average streamflow follow normal distribution!!! 7
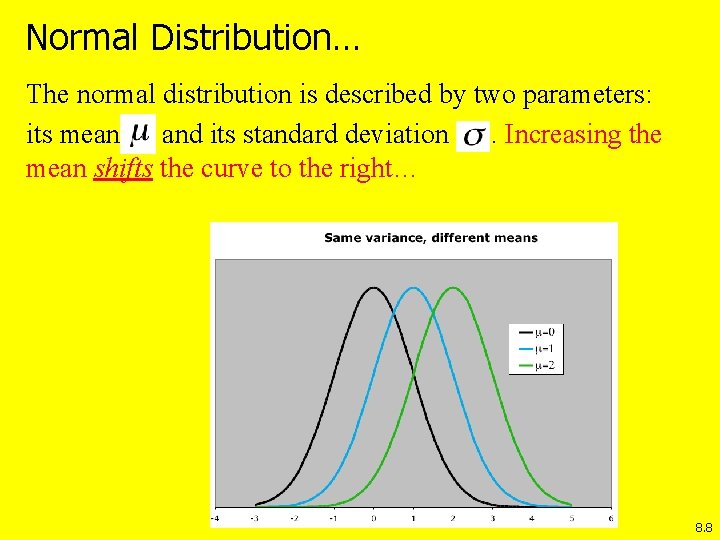
Normal Distribution… The normal distribution is described by two parameters: its mean and its standard deviation. Increasing the mean shifts the curve to the right… 8. 8
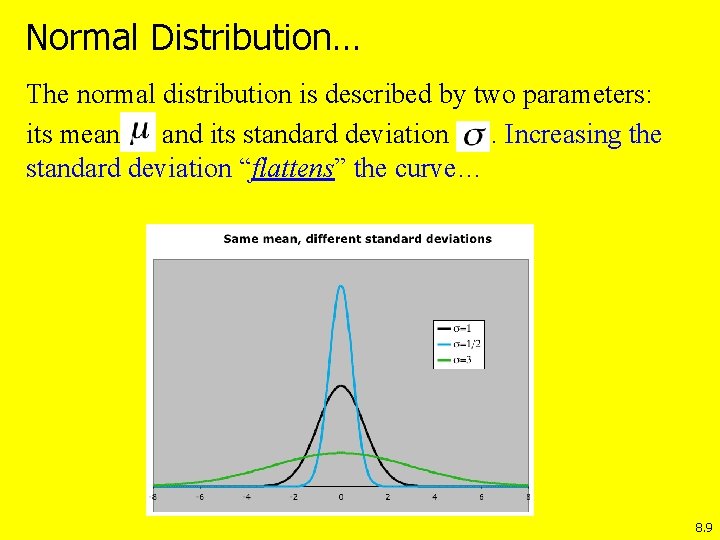
Normal Distribution… The normal distribution is described by two parameters: its mean and its standard deviation. Increasing the standard deviation “flattens” the curve… 8. 9
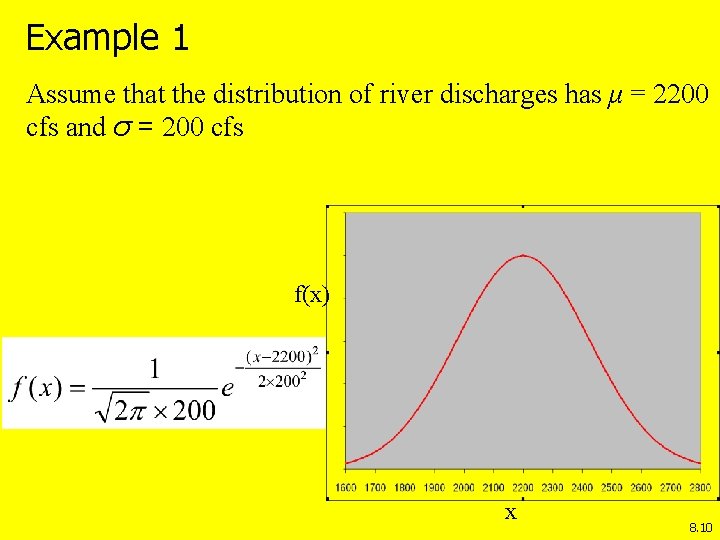
Example 1 Assume that the distribution of river discharges has μ = 2200 cfs and σ = 200 cfs f(x) x 8. 10
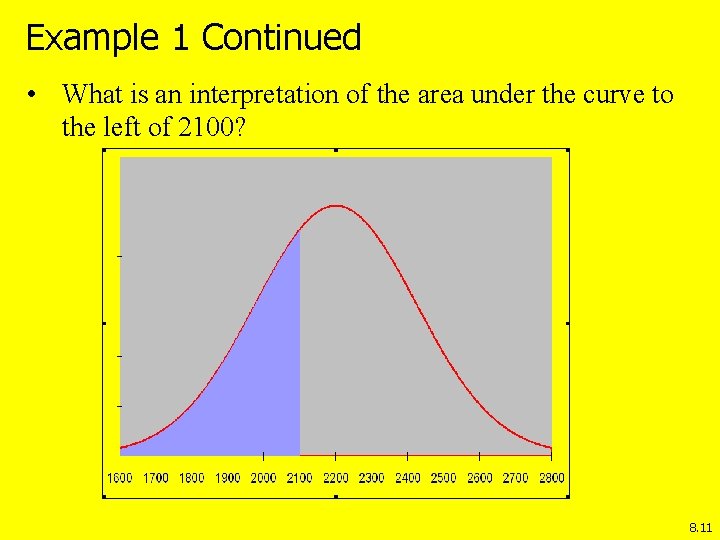
Example 1 Continued • What is an interpretation of the area under the curve to the left of 2100? 8. 11
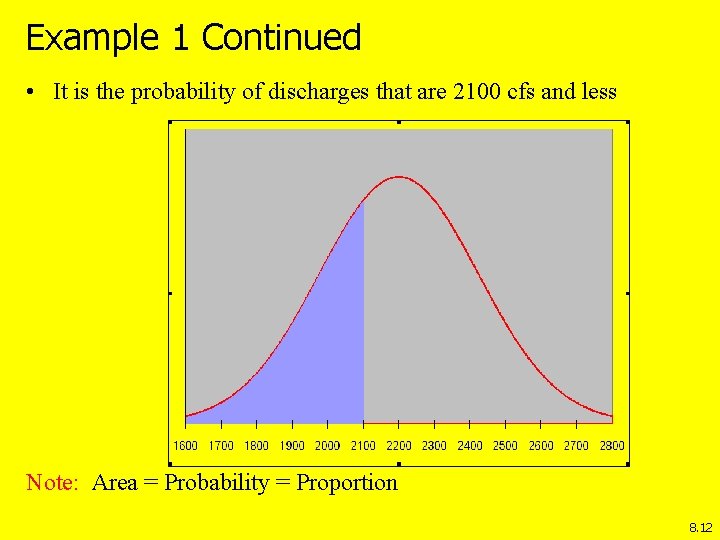
Example 1 Continued • It is the probability of discharges that are 2100 cfs and less Note: Area = Probability = Proportion 8. 12
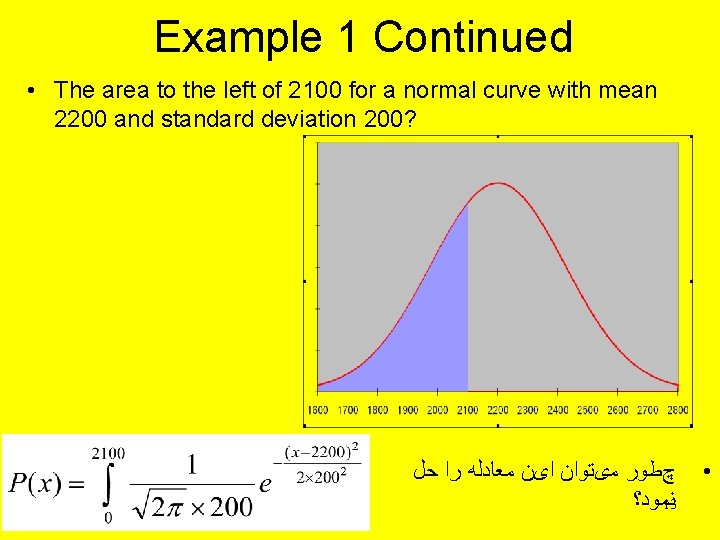
Example 1 Continued • The area to the left of 2100 for a normal curve with mean 2200 and standard deviation 200? چﻄﻮﺭ ﻣیﺘﻮﺍﻥ ﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺣﻞ ﻧﻤﻮﺩ؟ 13 •

Standard Normal Distribution 14

Standard Normal Distribution… • A normal distribution whose mean is zero and standard deviation is one is called the standard normal distribution. 1 0 1 • Any normal distribution can be converted to a standard normal distribution with simple algebra. This makes 15 calculations much easier.

Convert X to Z • Values of X Values of Z • If x is a value for X, then: is a value for Z • This is a very useful relationship 16

Find P(X < x) from P(Z < z) • This relationship lets us compute all different types of probabilities • Probabilities for X are directly related to probabilities for Z using the (X – μ) / σ relationship 17
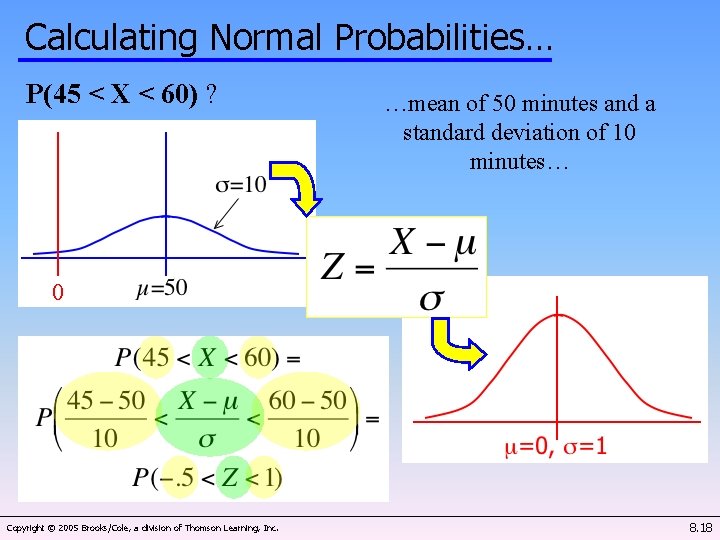
Calculating Normal Probabilities… P(45 < X < 60) ? …mean of 50 minutes and a standard deviation of 10 minutes… 0 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 18

Find P(X < x) from P(Z < z) • Because of this relationship Values of X Values of Z then P(X < x) = P(Z < z) • To find P(X < x) for a general normal random variable, we could calculate P(Z < z) for a corresponding standard normal random variable 19
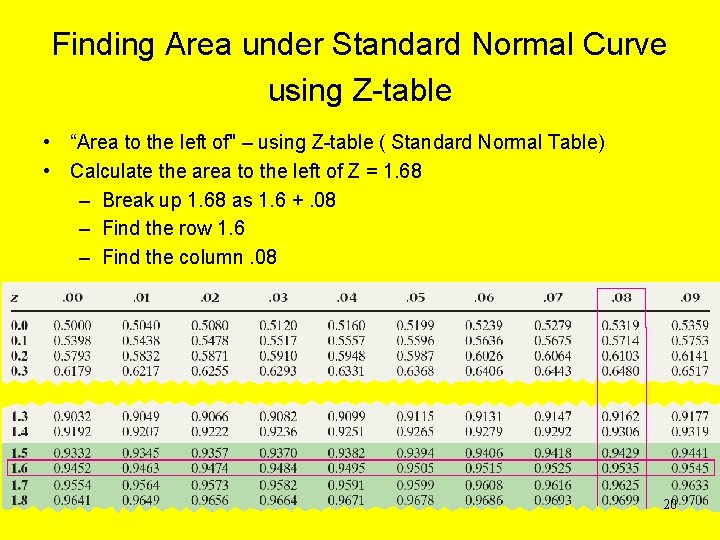
Finding Area under Standard Normal Curve using Z-table • “Area to the left of" – using Z-table ( Standard Normal Table) • Calculate the area to the left of Z = 1. 68 – Break up 1. 68 as 1. 6 +. 08 – Find the row 1. 6 – Find the column. 08 • The probability is 0. 9535 Note: The table always covers the area to the left of the Z score. 20

Example 2 For example: What’s the probability of getting a TOFEL score of 575 or less, =500 and =50? li. e. , A score of 575 is 1. 5 standard deviations above the mean Estimating this integral is tedious!!! But to look up P(Z < 1. 5) in standard normal chart (or enter into Excel or Matlab) no problem! P=. 9345 8. 21
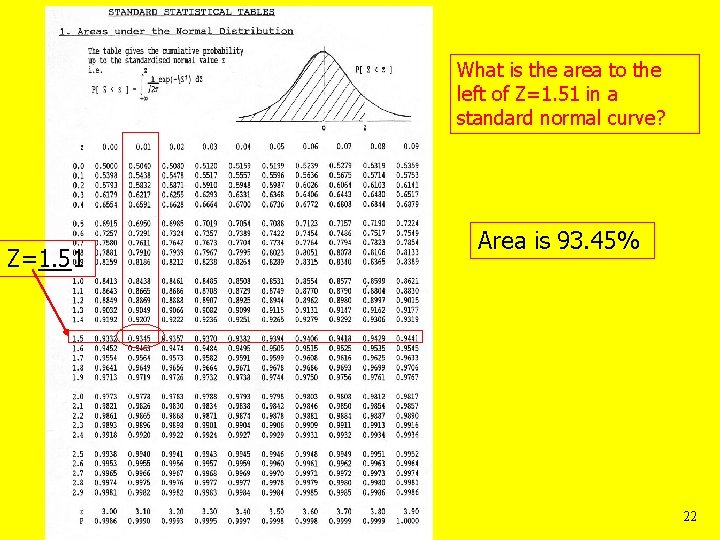
What is the area to the left of Z=1. 51 in a standard normal curve? Z=1. 51 Area is 93. 45% 22

Compute Area under Standard Normal Curve • Three different area calculations – Find the area to the left of – Find the area to the right of – Find the area between P(X < x 2) P(X > x 1) P(x 1< X < x 2) • Two different methods shown here: – From a table – Using Excel (recommended method) 23
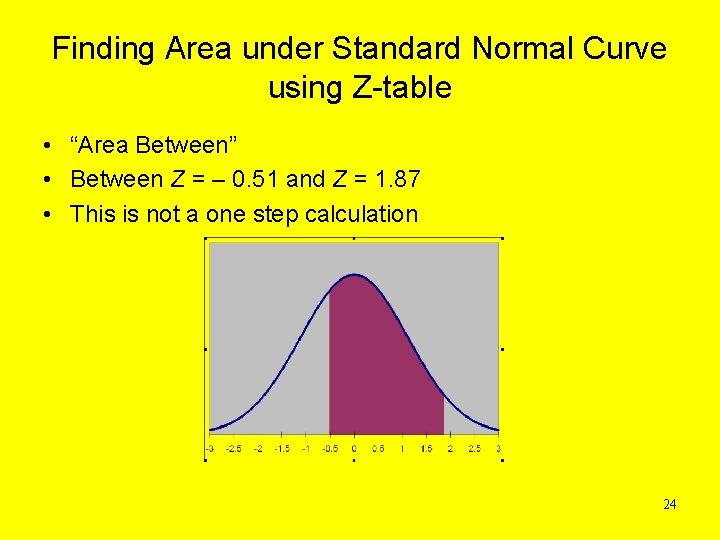
Finding Area under Standard Normal Curve using Z-table • “Area Between” • Between Z = – 0. 51 and Z = 1. 87 • This is not a one step calculation 24
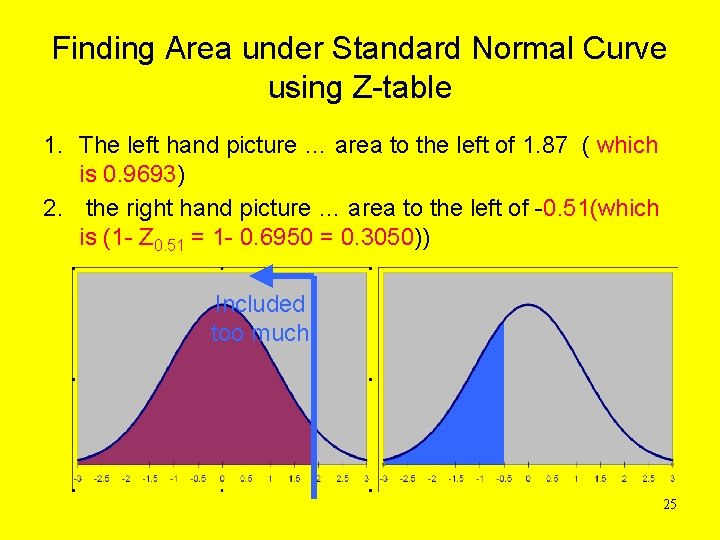
Finding Area under Standard Normal Curve using Z-table 1. The left hand picture … area to the left of 1. 87 ( which is 0. 9693) 2. the right hand picture … area to the left of -0. 51(which is (1 - Z 0. 51 = 1 - 0. 6950 = 0. 3050)) Included too much 25

Finding Area under Standard Normal Curve using Z-table • Area between Z = – 0. 51 and Z = 1. 87…. 0. 9693 – 0. 3050 = 0. 6643 We want We start out with, but it’s too much We correct by Area = 0. 9693 Area=0. 3050 26
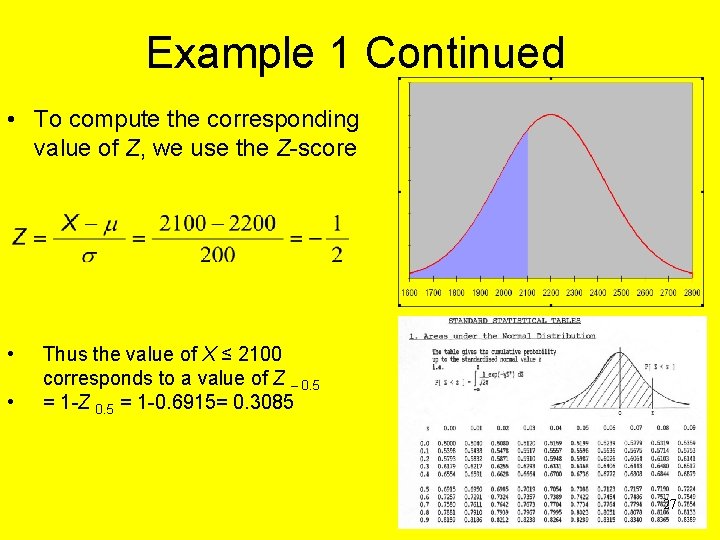
Example 1 Continued • To compute the corresponding value of Z, we use the Z-score • • Thus the value of X ≤ 2100 corresponds to a value of Z – 0. 5 = 1 -Z 0. 5 = 1 -0. 6915= 0. 3085 27

Using the Normal Table What is P(Z > 1. 6) ? z 0 1. 6 P(Z > 1. 6) =1 - P(Z < 1. 6). 0548 8. 28
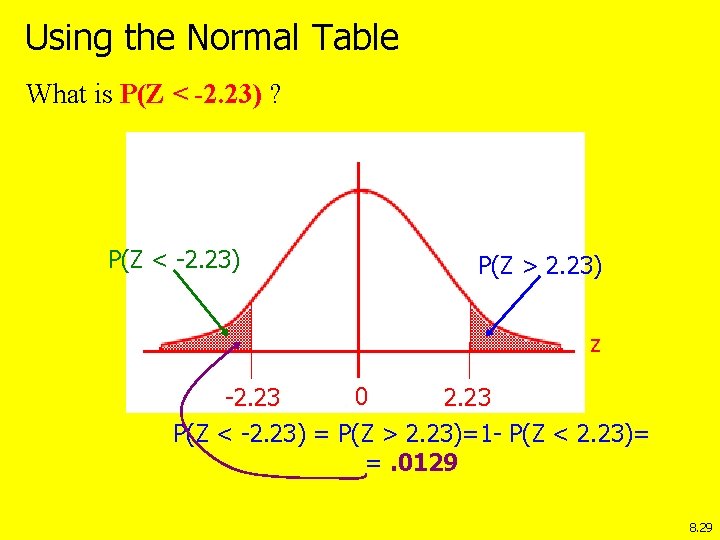
Using the Normal Table What is P(Z < -2. 23) ? P(Z < -2. 23) P(Z > 2. 23) z -2. 23 0 2. 23 P(Z < -2. 23) = P(Z > 2. 23)=1 - P(Z < 2. 23)= =. 0129 8. 29

Using the Normal Table What is P(Z < 1. 52) ? P(0 < Z < 1. 52) P(Z < 0) =. 5 z 0 1. 52 P(Z < 1. 52) =. 9357 8. 30
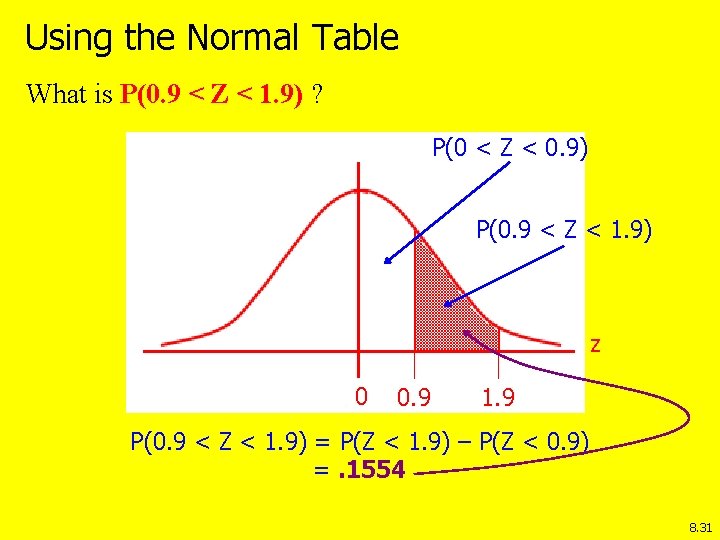
Using the Normal Table What is P(0. 9 < Z < 1. 9) ? P(0 < Z < 0. 9) P(0. 9 < Z < 1. 9) z 0 0. 9 1. 9 P(0. 9 < Z < 1. 9) = P(Z < 1. 9) – P(Z < 0. 9) =. 1554 8. 31
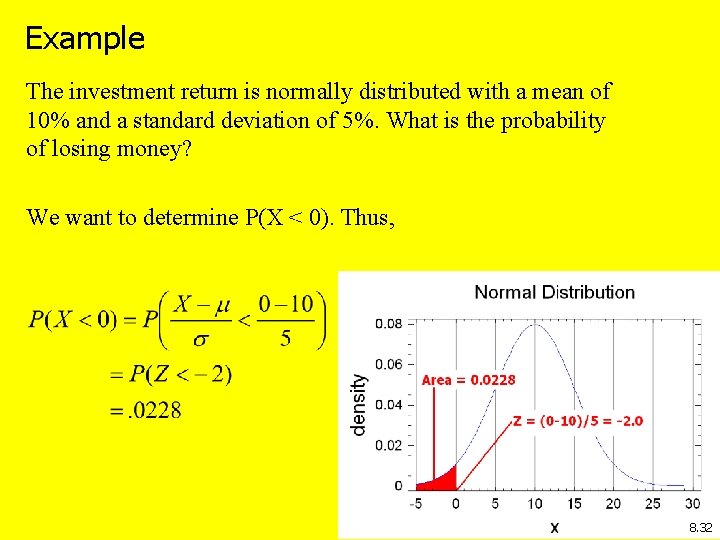
Example The investment return is normally distributed with a mean of 10% and a standard deviation of 5%. What is the probability of losing money? We want to determine P(X < 0). Thus, 8. 32
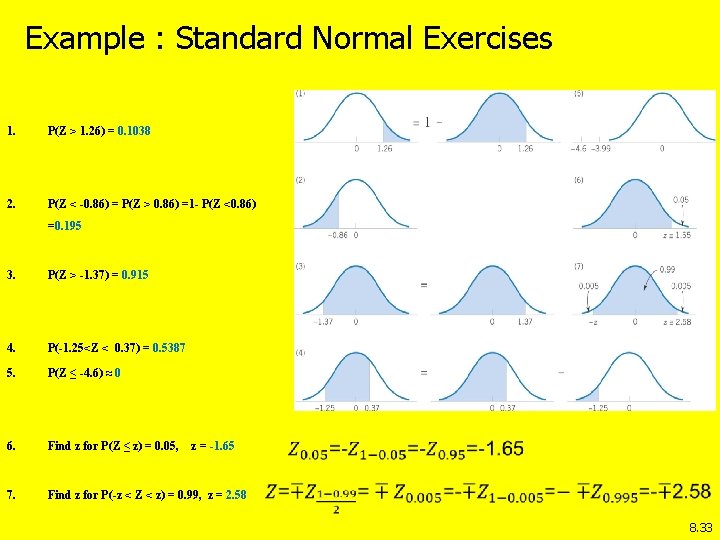
Example : Standard Normal Exercises 1. P(Z > 1. 26) = 0. 1038 2. P(Z < -0. 86) = P(Z > 0. 86) =1 - P(Z <0. 86) =0. 195 3. P(Z > -1. 37) = 0. 915 4. P(-1. 25<Z < 0. 37) = 0. 5387 5. P(Z ≤ -4. 6) ≈ 0 6. Find z for P(Z ≤ z) = 0. 05, 7. Find z for P(-z < Z < z) = 0. 99, z = 2. 58 z = -1. 65 8. 33
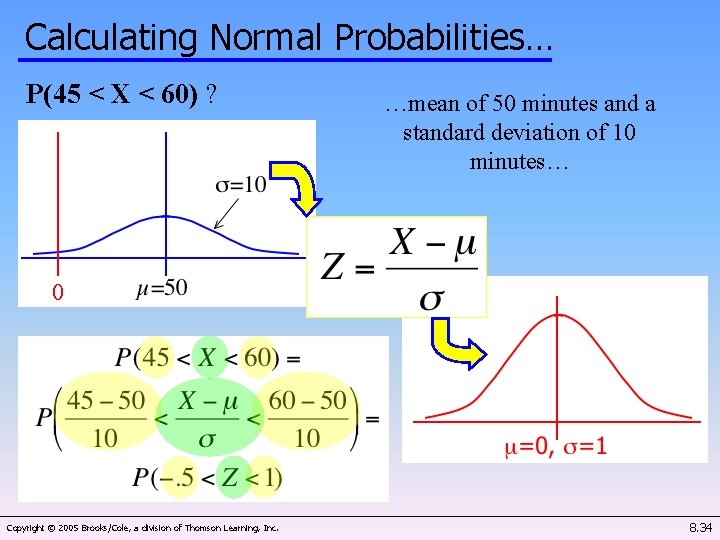
Calculating Normal Probabilities… P(45 < X < 60) ? …mean of 50 minutes and a standard deviation of 10 minutes… 0 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 34
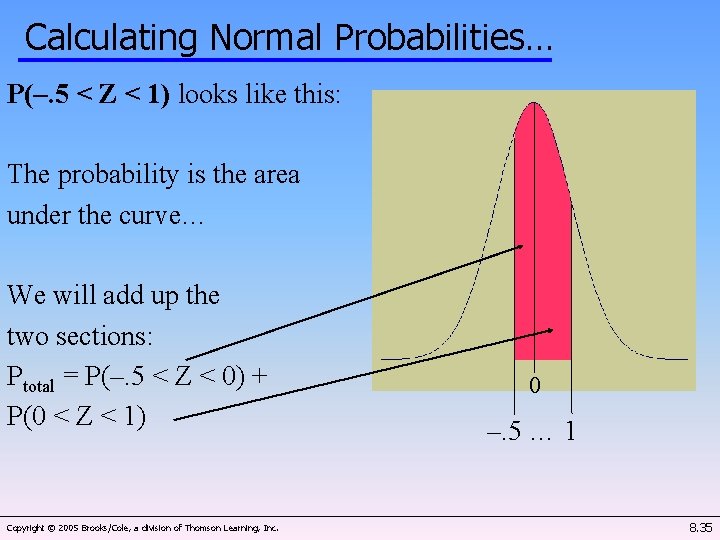
Calculating Normal Probabilities… P(–. 5 < Z < 1) looks like this: The probability is the area under the curve… We will add up the two sections: Ptotal = P(–. 5 < Z < 0) + P(0 < Z < 1) Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 0 –. 5 … 1 8. 35

Compute Area under Standard Normal Curve • Three different area calculations – Find the area to the left of – Find the area to the right of – Find the area between • Two different methods shown here: – From a table – Using Excel (recommended method) P(X < x 2) P(X > x 1) P(x 1< X < x 2) 36
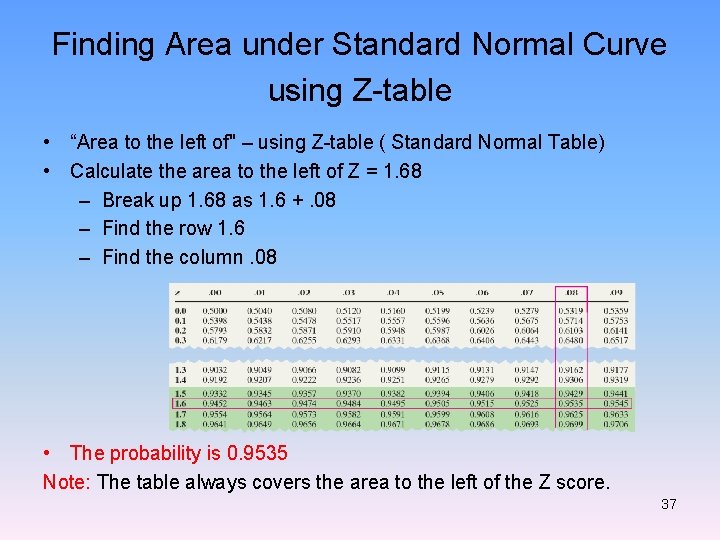
Finding Area under Standard Normal Curve using Z-table • “Area to the left of" – using Z-table ( Standard Normal Table) • Calculate the area to the left of Z = 1. 68 – Break up 1. 68 as 1. 6 +. 08 – Find the row 1. 6 – Find the column. 08 • The probability is 0. 9535 Note: The table always covers the area to the left of the Z score. 37

Example For example: What’s the probability of getting a TOFEL score of 575 or less, =500 and =50? li. e. , A score of 575 is 1. 5 standard deviations above the mean YA GHAMAR BANI HASHEM!!! But to look up Z = 1. 5 in standard normal chart (or enter into Excel or Matlab) no problem! P=. 9332 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 38
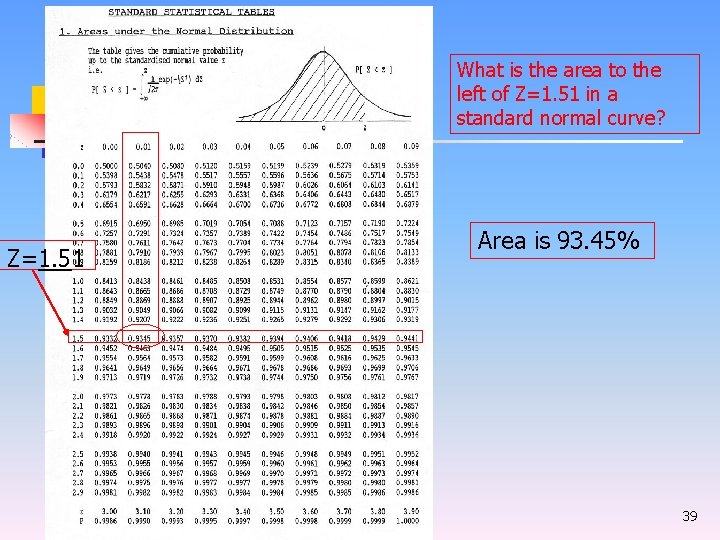
What is the area to the left of Z=1. 51 in a standard normal curve? Z=1. 51 Area is 93. 45% 39
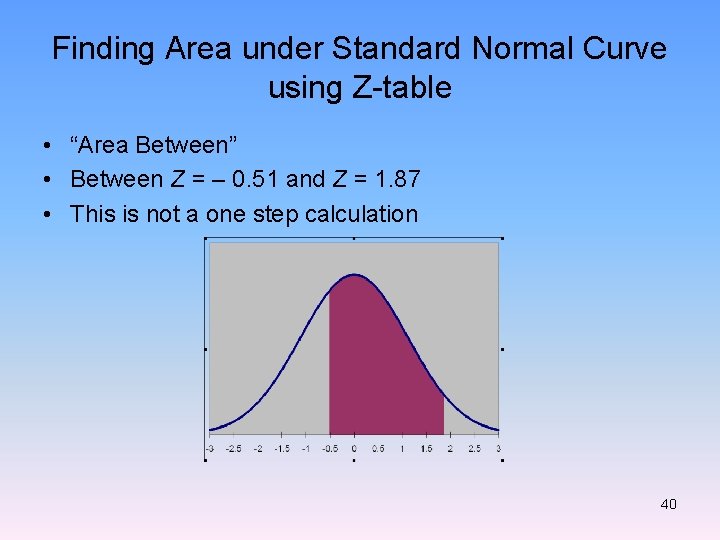
Finding Area under Standard Normal Curve using Z-table • “Area Between” • Between Z = – 0. 51 and Z = 1. 87 • This is not a one step calculation 40
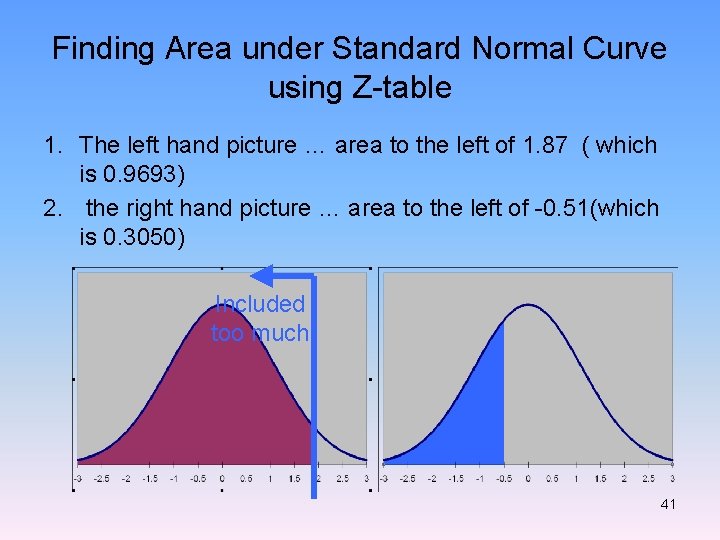
Finding Area under Standard Normal Curve using Z-table 1. The left hand picture … area to the left of 1. 87 ( which is 0. 9693) 2. the right hand picture … area to the left of -0. 51(which is 0. 3050) Included too much 41
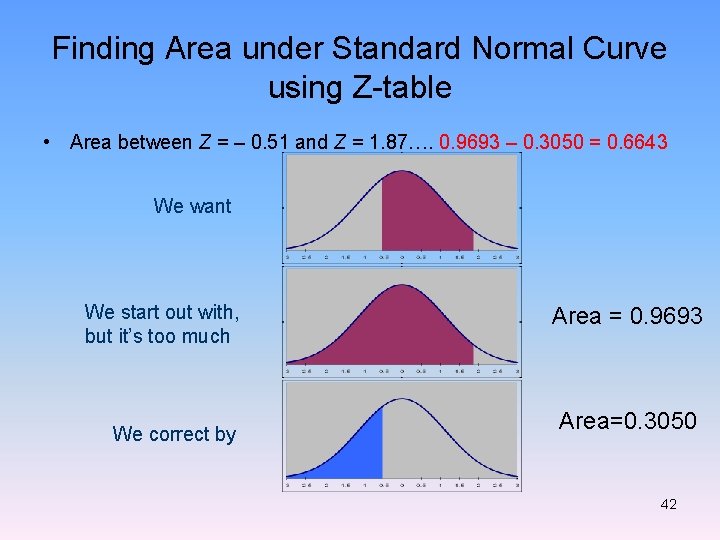
Finding Area under Standard Normal Curve using Z-table • Area between Z = – 0. 51 and Z = 1. 87…. 0. 9693 – 0. 3050 = 0. 6643 We want We start out with, but it’s too much We correct by Area = 0. 9693 Area=0. 3050 42

Finding Area under Standard Normal Curve using Z- Table • The area between -0. 51 and 1. 87 § The area to the left of 1. 87, or 0. 9693 … minus § The area to the left of -0. 51, or 0. 3050 … which equals § The difference of 0. 6643 • Thus the area under the standard normal curve between -0. 51 and 1. 87 is 0. 6643 43
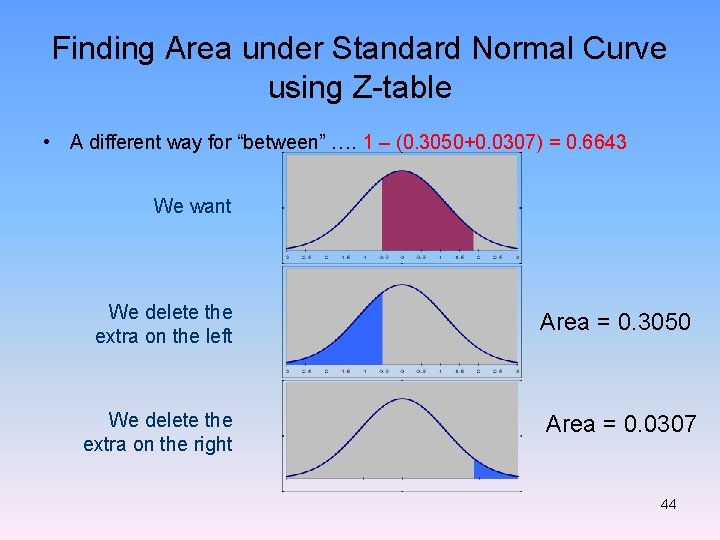
Finding Area under Standard Normal Curve using Z-table • A different way for “between” …. 1 – (0. 3050+0. 0307) = 0. 6643 We want We delete the extra on the left Area = 0. 3050 We delete the extra on the right Area = 0. 0307 44

Finding Area under Standard Normal Curve using Z-table • The area between -0. 51 and 1. 87 – The area to the left of -0. 51, or 0. 3050 … plus – The area to the right of 1. 87, or 0. 0307 … which equals – The total area to get rid of which equals 0. 3357 • Thus the area under the standard normal curve between -0. 51 and 1. 87 is 1 – 0. 3357 = 0. 6643 45
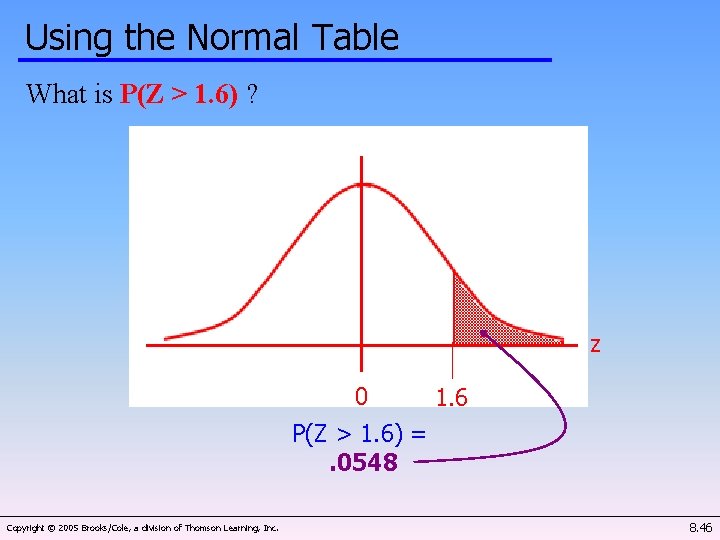
Using the Normal Table What is P(Z > 1. 6) ? z 0 1. 6 P(Z > 1. 6) =. 0548 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 46
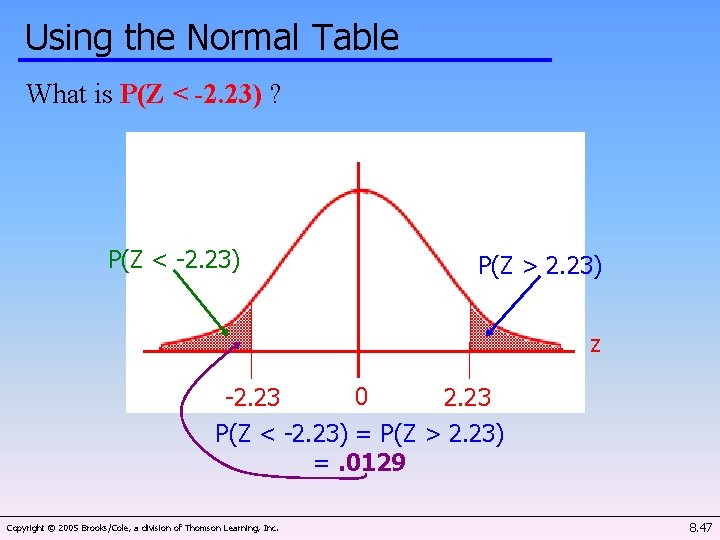
Using the Normal Table What is P(Z < -2. 23) ? P(Z < -2. 23) P(Z > 2. 23) z -2. 23 0 2. 23 P(Z < -2. 23) = P(Z > 2. 23) =. 0129 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 47
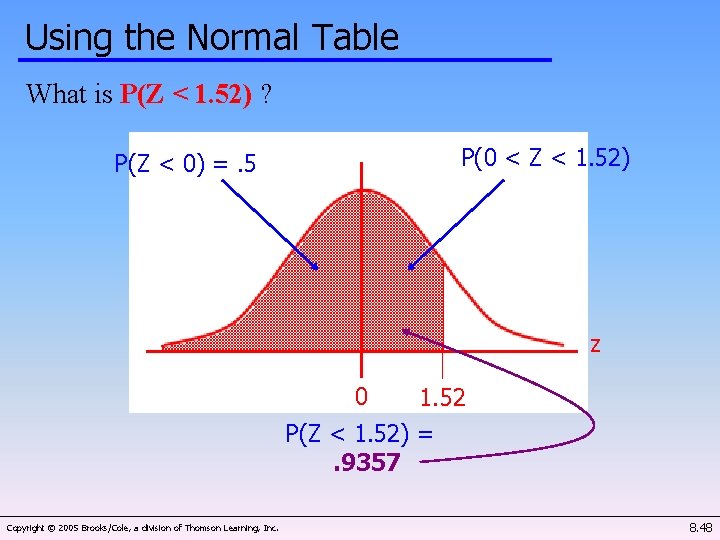
Using the Normal Table What is P(Z < 1. 52) ? P(0 < Z < 1. 52) P(Z < 0) =. 5 z 0 1. 52 P(Z < 1. 52) =. 9357 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 48
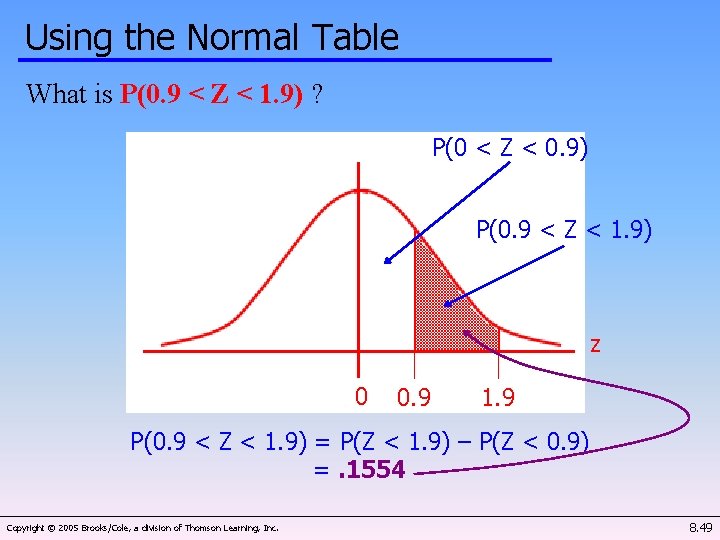
Using the Normal Table What is P(0. 9 < Z < 1. 9) ? P(0 < Z < 0. 9) P(0. 9 < Z < 1. 9) z 0 0. 9 1. 9 P(0. 9 < Z < 1. 9) = P(Z < 1. 9) – P(Z < 0. 9) =. 1554 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 49

Example The return on investment is normally distributed with a mean of 10% and a standard deviation of 5%. What is the probability of losing money? We want to determine P(X < 0). Thus, Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 50
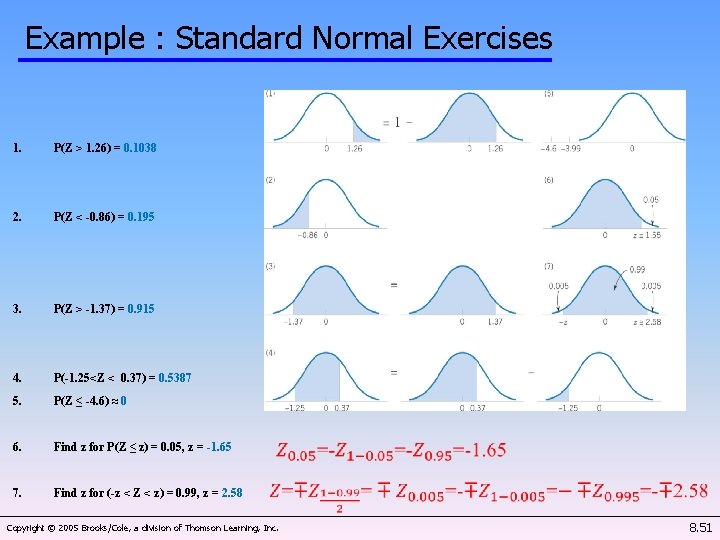
Example : Standard Normal Exercises 1. P(Z > 1. 26) = 0. 1038 2. P(Z < -0. 86) = 0. 195 3. P(Z > -1. 37) = 0. 915 4. P(-1. 25<Z < 0. 37) = 0. 5387 5. P(Z ≤ -4. 6) ≈ 0 6. Find z for P(Z ≤ z) = 0. 05, z = -1. 65 7. Find z for (-z < Z < z) = 0. 99, z = 2. 58 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 51
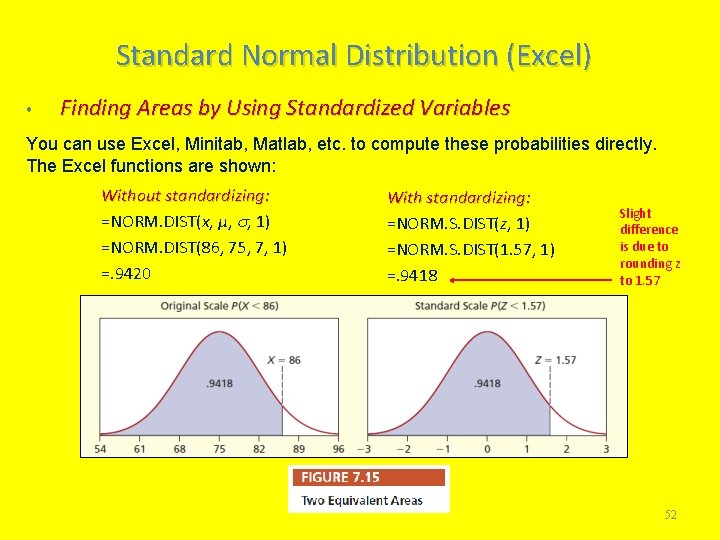
Standard Normal Distribution (Excel) • Finding Areas by Using Standardized Variables You can use Excel, Minitab, Matlab, etc. to compute these probabilities directly. The Excel functions are shown: Without standardizing: =NORM. DIST(x, µ, , 1) =NORM. DIST(86, 75, 7, 1) =. 9420 With standardizing: =NORM. S. DIST(z, 1) =NORM. S. DIST(1. 57, 1) =. 9418 Slight difference is due to rounding z to 1. 57 52
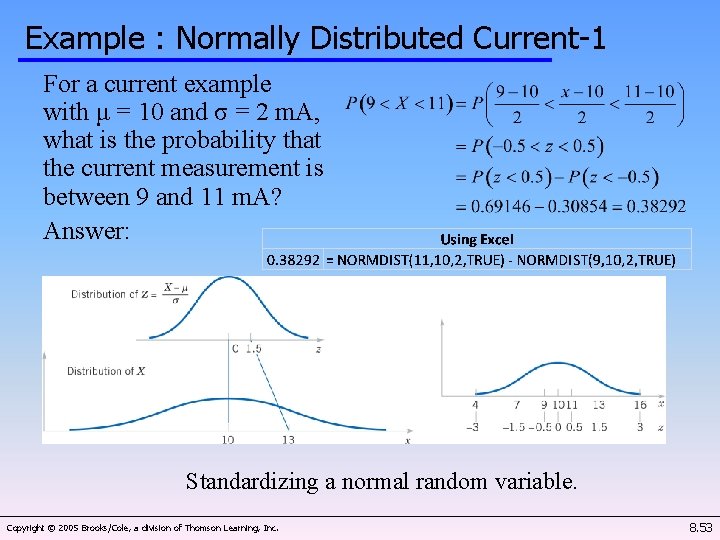
Example : Normally Distributed Current-1 For a current example with μ = 10 and σ = 2 m. A, what is the probability that the current measurement is between 9 and 11 m. A? Answer: Standardizing a normal random variable. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8. 53

Example The weights of packages of ground beef are normally distributed with mean 1 pound and standard deviation. 10. What is the probability that a randomly selected package weighs between 0. 80 and 0. 85 pounds?

Example What is the weight of a package such that only 5% of all packages exceed this weight?
Example A Company produces “ 20 ounce” jars of a picante sauce. The true amounts of sauce in the jars of this brand sauce follow a normal distribution. Suppose the companies “ 20 ounce” jars follow a normally distribution with a mean =20. 2 ounces with a standard deviation =0. 125 ounces.
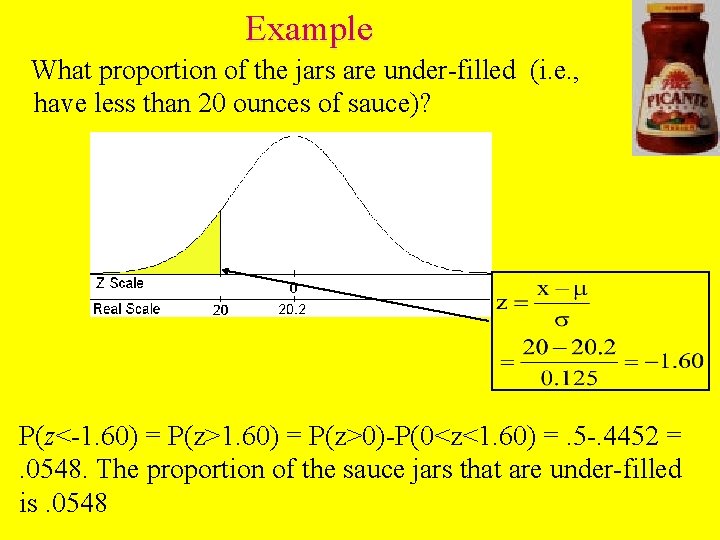
Example What proportion of the jars are under-filled (i. e. , have less than 20 ounces of sauce)? P(z<-1. 60) = P(z>0)-P(0<z<1. 60) =. 5 -. 4452 =. 0548. The proportion of the sauce jars that are under-filled is. 0548

Example What proportion of the sauce jars contain between 20 and 20. 3 ounces of sauce. P(-1. 60<z<. 80) = P(-1. 60<z<0)+P(0<z<. 80) = P(0<z<1. 60)+P(0<z<. 80)=. 4452+. 2881=. 7333 P(-1. 60<z<. 80) = P(z<. 80)-P(z<-1. 60)=. 5+P(0<z<. 80)[. 5 -P(0<z<1. 60)]=P(0<z<1. 60)+P(0<z<. 80)=. 7333

Example 99% of the jars of this brand of picante sauce will contain more than what amount of sauce?

Assignment 3 1. 2. 3. Assume your data are normally distributed. Find the probability that your variable is larger than half of the mean (first quartile), larger than mean, and larger than 3/2 mean based on mentioned probability density functions. Your discharge will be less than what quantity with the probability of 45%, 65%, and 99%? Note 7 of 5 E
- Slides: 60