Continuous Opacity Sources Continuous Opacity Sources Principal Sources

























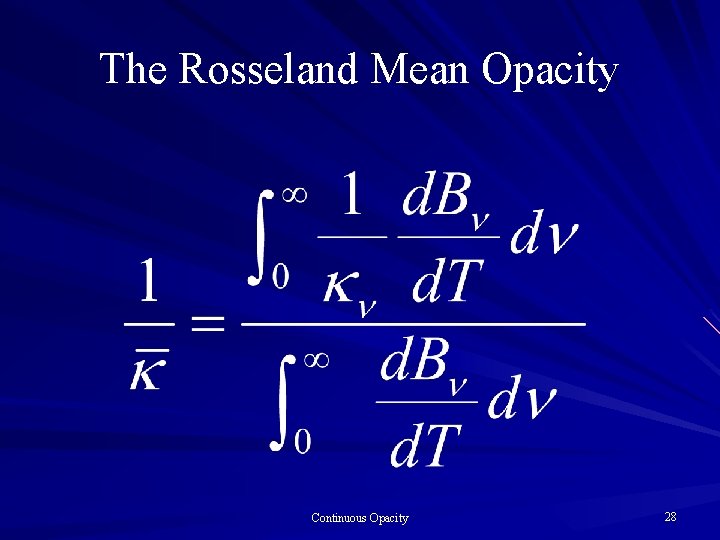



- Slides: 31

Continuous Opacity Sources

Continuous Opacity Sources Principal Sources: – – – Bound-Bound Transitions Bound-Free-Free (Bremstralung) Electron Scattering (Thompson & Compton) Molecular Transitions We consider only H or H-Like cases – We will do this classically (and correct to the QM result) – Stars are mostly H (in one form or another). Continuous Opacity 2

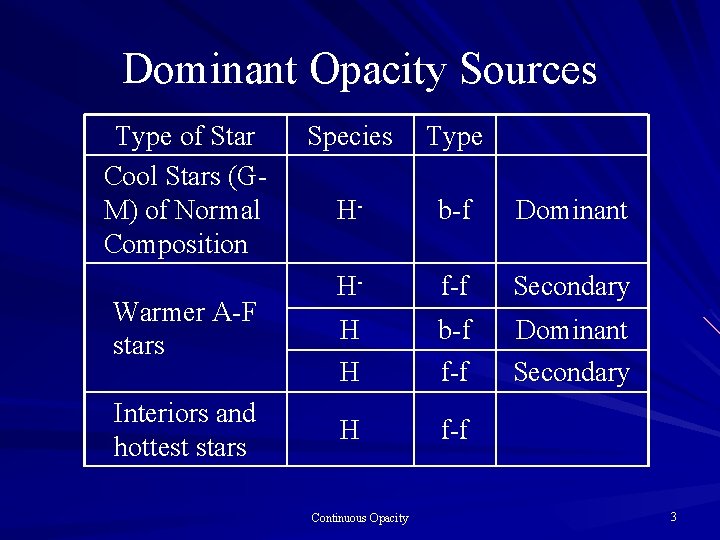
Dominant Opacity Sources Type of Star Cool Stars (GM) of Normal Composition Warmer A-F stars Interiors and hottest stars Species Type H- b-f Dominant H- f-f Secondary H H b-f f-f Dominant Secondary H f-f Continuous Opacity 3

Caveats and Details At High Temperatures: (1 -e-hν/k. T) → 0 so all of the bb, bf, and ff sources go to 0! Electron scattering takes over (is always there and may be important). – Free-Free is not the same as electron scattering: Conservation of momentum says a photon cannot be absorbed by a free particle! In principal we start with a QM description of the photon - electron interaction which yields the cross section for absorption/scattering of the photon of energy hν, call the cross section ai(ν). Continuous Opacity 4

The Opacity Is The opacity (g/cm 2) for the process is Κi(ν) = niai(ν)/ρ ni is the number density (#/cm 3) of the operant particles The subscript i denotes a process/opacity The total opacity is Κtotal = ∑Κi(ν) Continuous Opacity 5

Compton Scattering This process is important only for high energy photons as the maximum change is 0. 024Å. Reference: Eisberg -- Fundamentals of Modern Physics p. 81 ff. Continuous Opacity 6

Electron Scattering Conditions Collision of an electron and a photon – Energy and Momentum Must be conserved In stellar atmospheres during photon-electron collisions the wavelength of the photon is increased (assume the Eelectron < Photon (hν)) – At 4000Å: hν = 4. 966(10 -12) ergs – ½ mv 2 < 5(10 -12) ergs ==> v < 108 cm/s – At 5000 K v. RMS = 6. 7(105) cm/s – At 100000 K v. RMS = 3(106) cm/s Continuous Opacity 7

Thompson Scattering Classical Electron Scattering Reference: Marion - Classical Electromagnetic Radiation p. 272 ff Low Energy Process: v << c Energy Absorbed from the EM field is a = acceleration of the electron: a = e. E/me and E is the magnitude of the electric field. Continuous Opacity 8

Thompson Scattering Field Energy Density = <E 2/4π> (Time Average) Energy Flux Per Electron = c <E 2/4π> Now Take the Time Average of (#): But that has to be the energy flux per electron times the cross section which is σT c <E 2/4π>. Continuous Opacity 9

The Thompson Cross Section At High Temperatures this breaks down: T ≥ 109 K Continuous Opacity 10

Electron Scattering Opacity Κ e = σT N e / ρ There is no frequency dependence! Scattering off other ions is unimportant: Cross Section Goes as (1/m)2 so for ions (1/Am. H)2 while for electrons it goes as (1/me)2 Ratio: Ions/Electrons = (me/Am. H)2 = (1/A(1840))2 < 10 -6 Continuous Opacity 11

Rayleigh Scattering: σR Scattering of a low energy photon by a bound electron. Classically: Rayleigh scattering occurs when a photon of energy less than the atomic energy spacing is absorbed. – The electron then oscillates about the unperturbed energy level (harmonically). – The electron reradiates the same photon but remains in the same energy state. Continuous Opacity 12

The Rayleigh Cross-Section The cross section is: σ = σT/(1 -(ν 0/ν)2)2 – Where hν is the photon energy – hν 0 is the restoring force for the oscillator When ν << ν 0: σR = σT (λ 0/λ)4 – Now since ν << ν 0 we have E << k. T – Which implies T ~ 1000 K for this process. Continuous Opacity 13

Free-Free Opacities Absorption Events Bremstralung – Electron moving in the field of an ion of charge Ze emits or absorbs a photon: Acceleration in field produces a photon of hν De-acceleration in field consumes a photon of hν Consider the Emission Process – Initial Electron Velocity: v′ – Final Electron Velocity: v Conservation of Energy Yields ½ me v 2 + hν = ½ me v′ 2 Continuous Opacity 14

Energy Considerations Energy Absorbed: d. E/dt = 2/3 (e 2/c 3) a 2 where a = e. E/me (a is the acceleration) Most energy is absorbed during the time t b / v′ when the electron is close to the ion – b is called the impact parameter – b is the distance of closest approach Acceleration is ~ Ze 2/meb 2 Eabs 2/3 (e 2/c 3) (Ze 2/meb 2)2 (b / v′) 2/3 ((Z 2 e 6)/(me 2 c 3 b 3 v′)) Continuous Opacity 15

Frequency Dependence Expand d. E/d. T in a Fourier Series Greatest contribution is when 2πνt 1 during time t b / v′ – Therefore 2πν b / v′ = 1 or 2πν = v′ / b The energy emitted per electron per ion in the frequency range d is – dqν = 2πb db Eabs Why? 2πb db is an area! – dqν = energy emitted per electron per ion per unit frequency Continuous Opacity 16

Bremstralung Energy Total Energy Emitted: nine v′f(v′)dv′ dqν – ni = Ion number density – ne = electron number density (note that the electron flux is ne v′f(v′)dv′) The reverse process defines the Bremstralung absorption coefficient aν giving the absorption per electron of velocity v from the radiation field. In TE: Photon Energy Density = Uνp = (4π/c) Bν(T) Continuous Opacity 17

The Absorption Coefficient Net energy absorbed must be the product of the photon flux (photon energy = hν) c. Uνpdν and ninef(v)dvaν and (1 -e-hν/k. T) or – c. Uνpdν ninef(v)dvaν (1 -e-hν/k. T) But in TE that must be equal to the emission: – c. Uνpdν ninef(v)dvaν (1 -e-hν/k. T) = nine v′f(v′)dv′ dqν aν = π/3 (Z 2 e 6)/(hc me 2 ν 3 v) This is off by 4/ 3 from the exact classical result. Continuous Opacity 18

The Bremstralung Opacity V is v in the previous equations This reduces to κff(ν) = 4/3 nine (2π/3 mek. T)1/2 ((Z 2 e 6)/(hc meν 3)) gff(ν) is the mean Gaunt factor and the result has been corrected to the exact classical result. Continuous Opacity 19

Bound Free Opacities Transition from a Bound State to Continuum or Visa Versa This process differs from the free-free case due to the discrete nature of one of the states Nth Discrete State: Then the electron capture/ionization process must satisfy: ½ me v 2 - En = hν Continuous Opacity 20

Bound Free V is the velocity of the ejected or absorbed electron. Semiclassical treatment of electron capture – Electron Initial Energy: ½ mev 2 and is positive – The energy decreases in the electric field as it accelerates seeing ion of charge Ze – Q: Why does it loose energy as it accelerates? – A: It radiates it away The energy loss per captured electron may be estimated as: – dqν = 2πbdb. Eabs = (8π2/3) ((Z 2 e 6)/(me 2 c 3 v′ 2 dν)) Continuous Opacity 21

Cross Section The cross section for emission of photons into frequency interval dν is defined by – hν dσν = dqν = hν (dσν/dν) dν The final state is discrete so define σcn as the cross section for capture into state n (energy En) characterized by n in the range (n, n+dn) so that dσν = σcndn. Then – hν (dσν/dν) = hν σcn dn/dν – Solve for σcn and use En = -IHZ 2/n 2 to get dn/dν Thus: σcn = ((2 IHZ 2/n 2)/(h 2νn 3))(dqν/dν) = (32/3) π4 ((Z 2 e 10)/(mec 3 h 4 v 2νn 3)) Continuous Opacity 22

Photoionization The reverse process is related by detailed balance Let σνn = photoionization cross section The number of photons absorbed of energy hν with the emission of electrons of energy ½mev 2 - En from the nth atomic state is – (c. Uνp/hν) dν σνn Nn (1 -e-hν/k. T) – Nn is the number of atoms in state n The reverse process: the number of electrons with initial velocities v captured per second into state n is Ni σcn ne v f(v) dv Continuous Opacity 23

State Population The Boltzmann Equation for the system is: where g 1 = 2 and gn = 2 n 2 (H-like ions) and the Saha equation is Detailed Balance says: (c. Uνp/hν)dνσνn. Nn(1 -e-hν/k. T) = Niσcnnevf(v)dv Continuous Opacity 24

The Bound Free Coefficient We assume – Maxwellian distribution of speeds – Boltzmann and Saha Equations σνn = (gi/gn) (mevc/hν)2 σcn We assume the Z-1 electrons in the atom do not participate, set gi = 1, and correct for QM then Continuous Opacity 25

Limits and Conditions Photon must have hν > En – σ = 0 for hν < En (= IHZ 2/n 2) Recombination – Levels coupled to ν by bound free processes have En for n > n* where n* = (IHZ 2/hν)1/2 Total Bound Free Opacity: Continuous Opacity 26

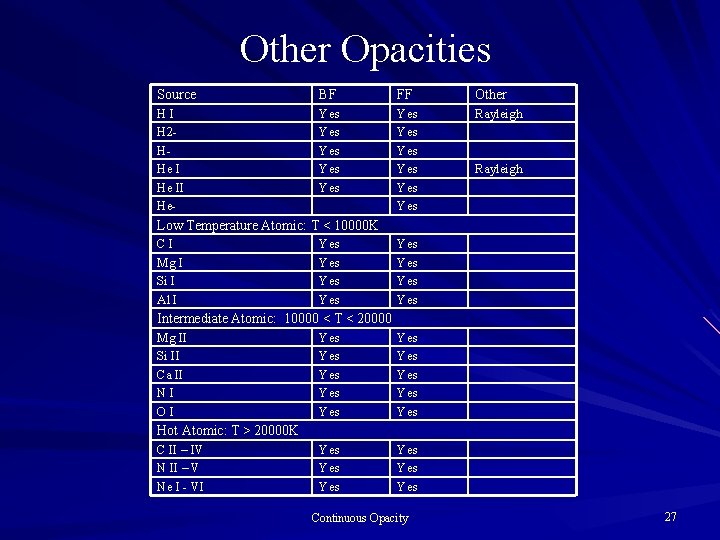
Other Opacities Source BF FF Other HI H 2 HHe II He- Yes Yes Yes Rayleigh Low Temperature Atomic: T < 10000 K CI Mg I Si I Al I Yes Yes Intermediate Atomic: 10000 < T < 20000 Mg II Si II Ca II NI OI Yes Yes Yes Yes Hot Atomic: T > 20000 K C II – IV N II – V Ne I - VI Continuous Opacity 27
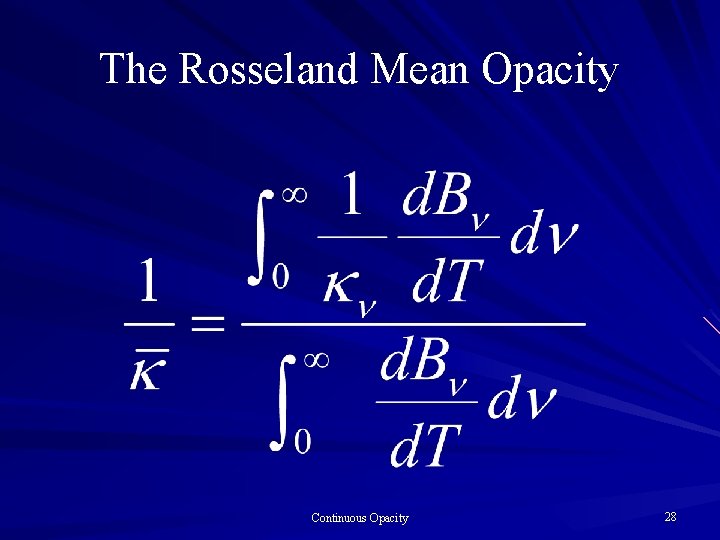
The Rosseland Mean Opacity Continuous Opacity 28

More Spectroscopic Notation H Like Only Electron and proton have – Spin ½ – Angular momentum /2 and each has a corresponding magnetic moment The magnetic moment of the electron interacts with both the orbital magnetic moment of the atom (spin-orbit) and the spin of the proton (spin-spin). – Spin-orbit: fine structure (multiplets) – Spin-spin: hyperfine structure Continuous Opacity 29

Notation Principal Quantum Number n Orbital Quantum Number l: l ≤ n - 1 – – l = S P D F 0 1 2 3 Total angular momentum of a state specified by l = l [(l+1)]½ Spin angular momentum (s=1/2): [s(s+1)]½ = 3 /2 Orbital and spin angular momentum interacts to produce a total angular momentum quantum number j = l ± 1/2: S States have j = 1/2, P states have j = 1/2, 3/2; and D has j = 3/2, 5/2 Continuous Opacity 30

H Like Notation Continuous Opacity 31