Continuous Growth and the Number e Lesson 3

Continuous Growth and the Number e Lesson 3. 4

Compounding Multiple Times Per Year • Given the following formula for compounding § P = initial investment § r = yearly rate § n = number of compounding periods § t = number of years

Compounding Multiple Times Per Year • What if we invested $1000 for 5 years at 4% interest • Try the formula for different numbers of compounding periods § Monthly § Weekly (n = 52) § Daily (n = 365) § Hourly (n = 365 * 24) What phenomenon do you notice?

Compounding Multiple Times Per Year • You should see that we seem to reach a limit as to how much multiple compounding periods increase the final amount • So we come up with continuous compounding

Using e As the Base • We have used • Consider letting y = A * Bt B = ek • Then by substitution • Recall B = (1 + r) • It turns out that y = A * (ek)t (the growth factor)

Continuous Growth • The constant k is called the continuous percent growth rate • For Q = a bt § k can be found by solving ek = b • Then Q = a ek*t • For positive a § if k > 0 then Q is an increasing function § if k < 0 then Q is a decreasing function

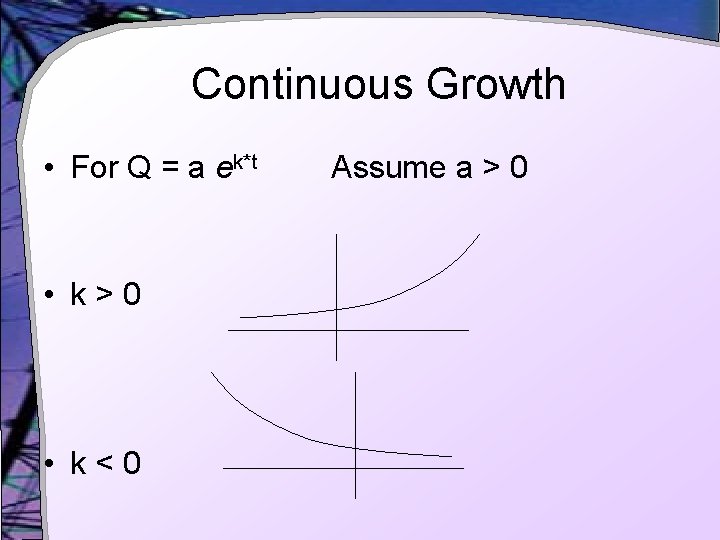
Continuous Growth • For Q = a ek*t • k>0 • k<0 Assume a > 0

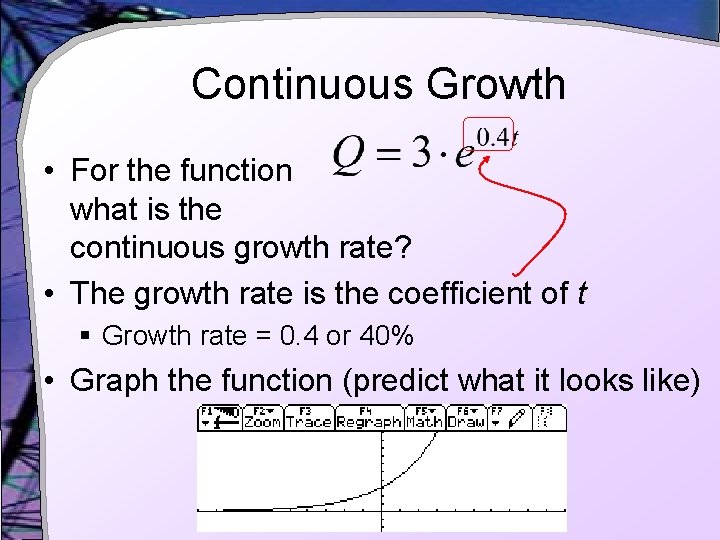
Continuous Growth • For the function what is the continuous growth rate? • The growth rate is the coefficient of t § Growth rate = 0. 4 or 40% • Graph the function (predict what it looks like)

Converting Between Forms • Change to the form Q = A*Bt • We know B = ek • Change to the form Q = A*ek*t • We will eventually discover that k = ln B

Assignment • Lesson 3. 4 • Page 133 • Exercises 1 – 25 odd