Continuous functions And limits POP If you have

POP. If you have to lift your pencil to make the graph then its

What is a limit? As x approaches from left X= As x approaches from

How to find the limit of certain functions The following slides will help you

Ways to find a limit Is the limit going to a constant? Ex. Is

Limit as x goes to a constant Is the function a polynomial function? YES

Limit as x goes to ∞ Is the function a polynomial function? YES Is

Then just plug in the value of x. Polynomial functions are continuous for all

Look at the highest degree of each polynomial. Is the highest degree in the

$Then the limit is the fraction of the leading coefficients Return$

Then the limit goes to zero The numerator grows slower than the denominator. It

The function needs to be factored, or simplified, or multiply by the conjugate of

Return The end Website • In general finding a limit of a function is

Slides: 19

Download presentation

Continuous functions And limits

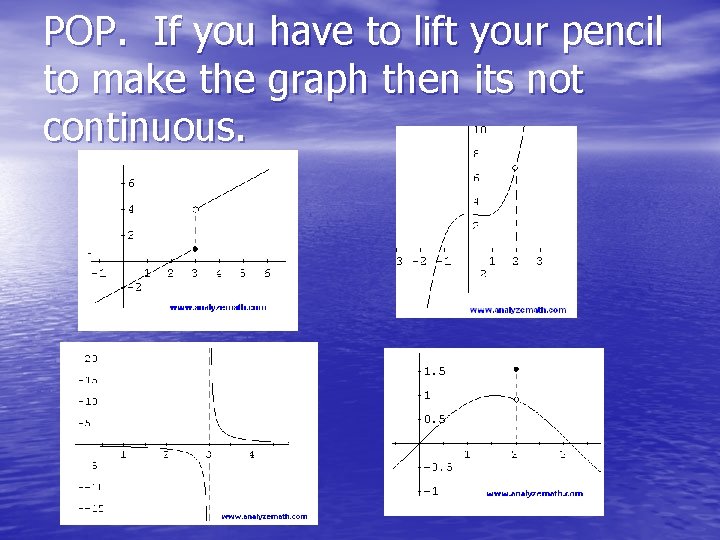
POP. If you have to lift your pencil to make the graph then its not continuous.

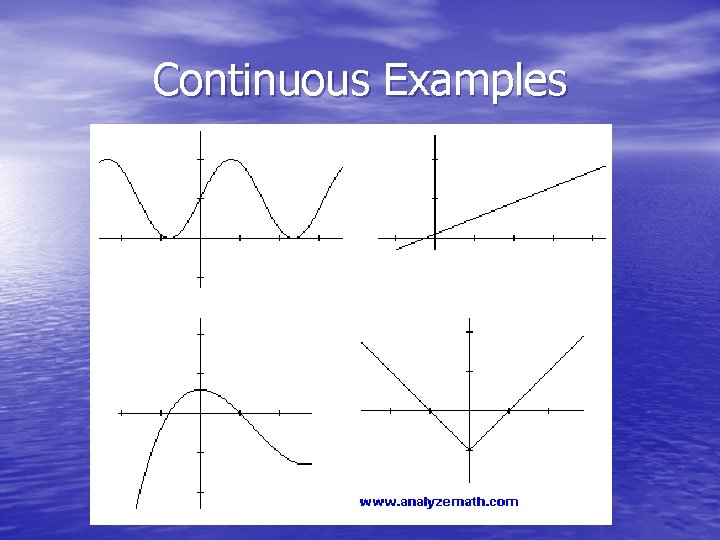
Continuous Examples

What is a limit? As x approaches from left X= As x approaches from right X 2+6 X= X 2+6 1 7 3 15 1. 9 9. 61 2. 1 10. 41 1. 99 9. 9601 2. 09 10. 3681 1. 999 9. 996001 2. 009 10. 03608 1. 9999 9. 9996 2. 0009 10. 0036 1. 99999 9. 99996 2. 00009 10. 00036 1. 999999 9. 999996 2. 000009 10. 00004

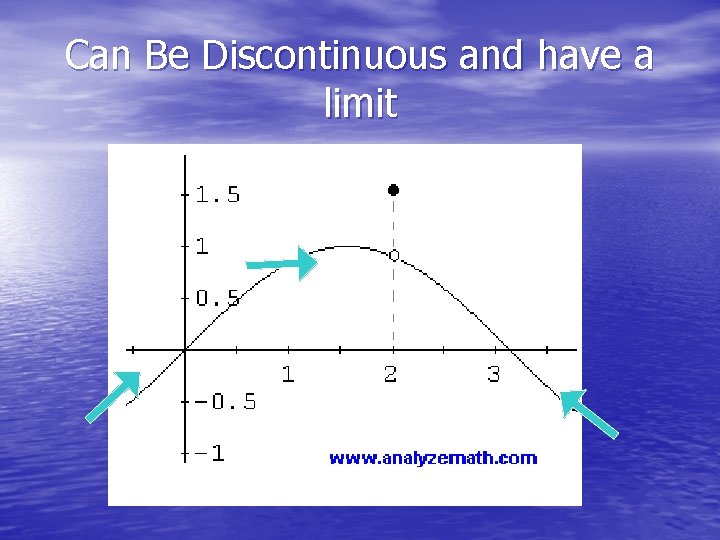
Can Be Discontinuous and have a limit

Discontinuous with one-sided limits

How to find the limit of certain functions The following slides will help you find the limit of some basic polynomial and rational functions. This will not help you find more complicated functions. Worst case scenario take values really close to the limit and see if there is a trend.

Ways to find a limit Is the limit going to a constant? Ex. Is the limit going to infinity? Ex. YES

Limit as x goes to a constant Is the function a polynomial function? YES Is the function a rational function with two polynomial functions? YES

Limit as x goes to ∞ Is the function a polynomial function? YES Is the function a rational function with two polynomial functions? YES

Then just plug in the value of x. Polynomial functions are continuous for all real numbers. Return

Plug in the value of x Do you get ? YES

Then the limit goes to zero. End Return

Look at the highest degree of each polynomial. Is the highest degree in the numerator? Is the highest degree in the denominator? YES Are the degrees the same in both denominator and numerator? YES None of the above? YES

Then the limit goes to infinity Return

$Then the limit is the fraction of the leading coefficients Return$

Then the limit is the fraction of the leading coefficients Return

Then the limit goes to zero The numerator grows slower than the denominator. It acts like 1/∞ Return

The function needs to be factored, or simplified, or multiply by the conjugate of the denominator. Then plug the value of x back in. You may also take values of x that are approaching what the limit is approaching. end Return

Return The end Website • In general finding a limit of a function is finding • • • the value of f(x) as x approaches a value. The left side and the right side limits must be the same in order for it to have a have limit at the point. The function does not have be continuous at the limit value. A graph of the function might be helpful to find the limit, but you cant always depend on them.