Continuous Collision Detection David Knott COMP 259 class

Continuous Collision Detection David Knott COMP 259 class presentation The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Interference vs. Collision • Most algorithms that we think of as collision detection are actually Interference Detection ♦ Interference Detection: Static setting ♦ Collision Detection: Dynamic setting • Most collision detection algorithms consist of repeated application of interference detection The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

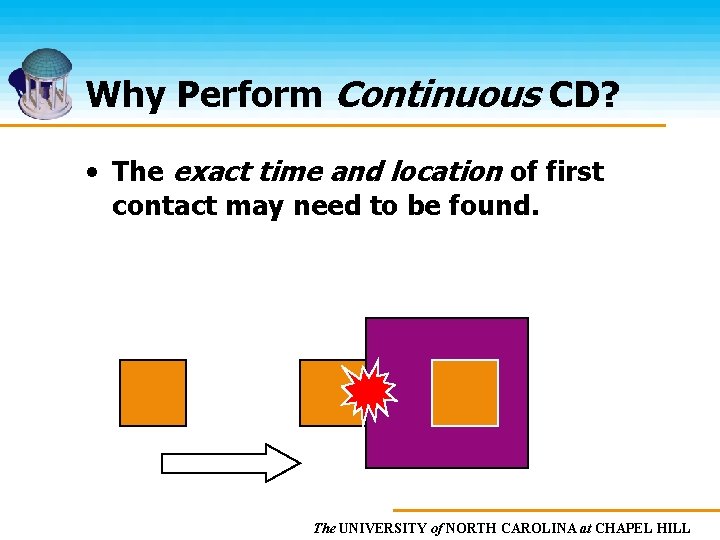
Why Perform Continuous CD? • The exact time and location of first contact may need to be found. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

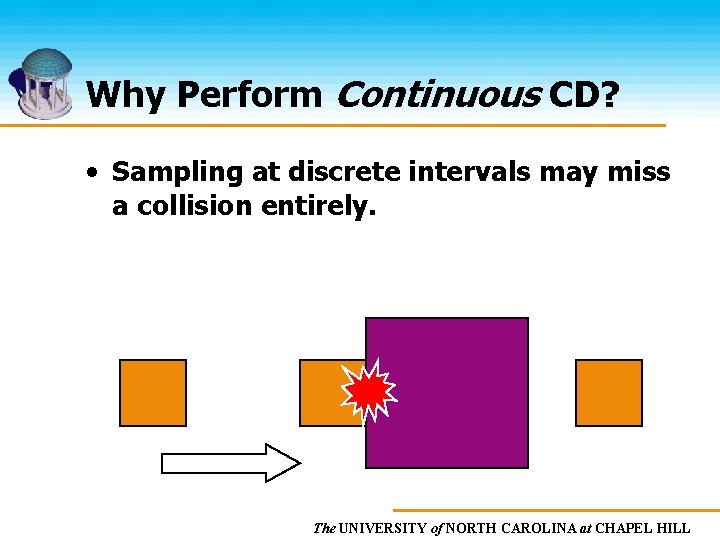
Why Perform Continuous CD? • Sampling at discrete intervals may miss a collision entirely. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

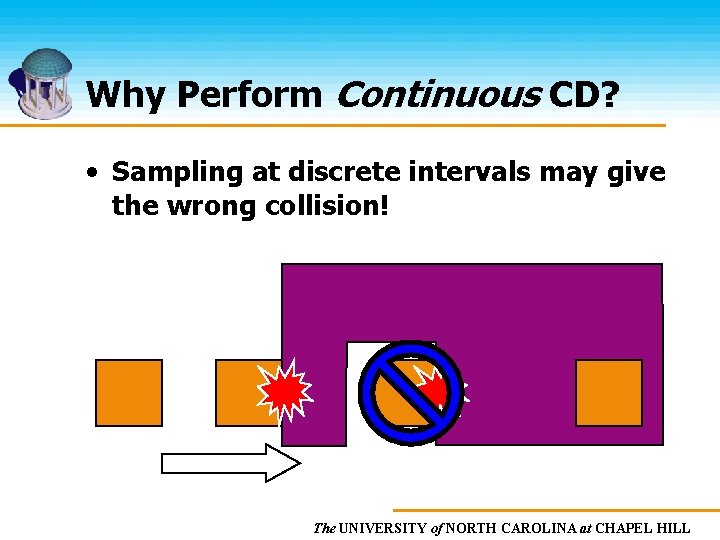
Why Perform Continuous CD? • Sampling at discrete intervals may give the wrong collision! The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Why Perform Continuous CD? • Most animation systems use backtracking methods ♦ Try to find point of first contact by binary search. ♦ Subject to all problems from previous slides ♦ Especially poor for non-solid objects (eg. cloth) The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Types of motion • Almost all CCD algorithms assume linear motion over a single time step • Non-linear motion makes CCD computation much more expensive ♦ True for both approximate and exact methods The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

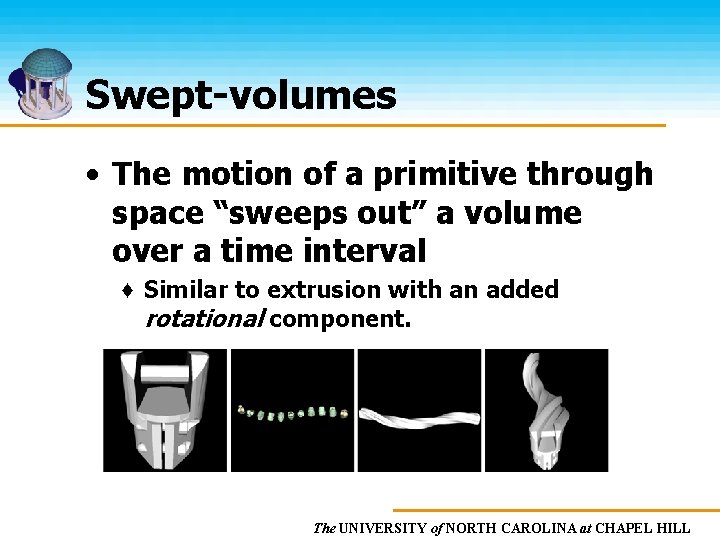
Swept-volumes • The motion of a primitive through space “sweeps out” a volume over a time interval ♦ Similar to extrusion with an added rotational component. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Swept Volumes • Swept-Volumes of moving objects may be compared against each other • This is a binary test for collision ♦ Does not reveal when or where collision occurs The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Swept Volumes • Swept volumes are a sufficient but not necessary condition for determining if objects are collision-free ♦ Swept volumes may overlap, even when the objects have not collided ♦ Subdivision is needed ♦ Or consider relative motion The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Swept volumes in 3 D space • 1 D - line • 2 D – prism a a b a' a' b' • 3 D ♦ becomes very complicated very quickly The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Swept Volumes • A object in n dimensions sweeps out a volume in n+1 dimensions • These volumes are very expensive to compute. ♦ Even harder with arbitrary rotations. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Swept Volumes Source: “Fast Swept Volume Approximation…” Y. Kim – ACM Solid Modelling 2003 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Approximate CCD • Rough (conservative) CCD tests can be performed via bounding volumes of the swept volumes • Hierarchies of bounding volumes may be constructed The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Convex Hulls of Swept Volumes “A Safe Swept-Volume Approach to Collision Detection” A. Foisy & V. Hayward Int. Symp. on Robotics Research 1994 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Convex Hulls of Swept Volumes • The AABB of a moving vertex • Can find the convex hull of the AABBs of all vertices The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Convex Hulls of Swept Volumes • The convex hull of vertex AABBs is also a convex approximation to the swept volume of the moving object But NOT the convex hull of the AABBs. • Can consider hierarchies of these The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Convex Hulls of Swept Volumes • Can compute bounding boxes of the motion of individual vertices ♦ From this, a convex approximation of the object’s swept volume is straightforward • If bounding volumes test positive, then individual polygon primitives must be tested ♦ Similar to discrete bounding volumes The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Four-Dimensional Extrusion • Extrude an object from N-dimensional space into N+1 dimensional space ♦ eg. 2 D object extruded through time to form 3 D object • “Collision Detection by 4 D Intersection Testing…” ♦ J. Cameron – IEEE Trans. Robotics & Automation - 1990 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Four-Dimensional Extrusion • Not the same as swept volumes ♦ Swept volumes compute sweep of the boundary of the surface ♦ 4 D extrusion computes sweep of volume ♦ Overlap of extruded volumes is a necessary and sufficient condition for collision. • Conceptually nice • Implementation is exceedingly difficult The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Exact CCD • Swept volumes and bounding volumes will only report potential collisions. • Still need to determine the exact time and point of collision. • The types of objects that are being tested are usually polygonal ♦ How can the exact tests be done for polyhedra? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Exact CCD: How may two polygons collide? • Vertex/Face Collision • Edge/Edge Collision The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Exact CCD • “Collision Detection for Moving Polyhedra” ♦ J. Canny – IEEE Patt. Anal. and Mach. Int. 1986 • CCD for both the edge/edge and vertex/face tests reduces to a system of constraints and solving a polynomial of degree 5 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Vertex/Face • Collision when vertex/face distance is zero • Check for point/plane coplanarity • Then check for vertex/face intersection validity The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Edge/Edge • Collision when edge/edge distance is zero • Check for line/line coplanarity • Then check for edge/edge intersection validity The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Edge/Edge and Vertex/Face • Note that both types of tests are of the form: ♦ Find when four points are co-planar (continuous) ♦ Check for validity at time of co-planarity (in-plane distance computation) • When two primitives have more than one contact during a single time step – choose the first one The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Co-Planarity Test • For both edge/edge and vertex/face, the test has the form: • Assuming linear motion, this equation is cubic in the time variable • May be solved directly for all triangle pairs • “Collision and Self-Collision Handling…” ♦ X. Provot - Graphics Interface 1997 ♦ Application: Cloth collision detection The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Solving the Equations • This could be solved directly. • Solving a cubic directly is difficult and expensive. • Most implementations use bisection or similar methods to find the roots of the equations. • Is there a better way to do this? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Interval Arithmetic • Compute with intervals instead of numbers • I = [a, b] = {x , a x b} • Vectors have interval components • Given a function f(x), then computation of f(I) results in another interval • • “Interval Analysis for Computer Graphics” “Interval Methods for Multi-Point Collisions…” ♦ J. Snyder – SIGGRAPH 1992/1993 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Interval Arithmetic Operations • [a, b] [c, d]= [a c, b d] • [a, b] [c, d]= [a d, b c] • [a, b] [c, d]= [min(ac, ad, bc, bd), max(ac, ad, bc, bd)] • 1/[a, b] = [1/b, 1/a] if a>0 or b<0 • [a, b] [c, d] if b c The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Interval Arithmetic - example • Consider the function: over the time interval [0, /2] • We have the bounds: • Therefore: The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Interval arithmetic • Function bounds are not exact ♦ But become tight as size of time interval approaches zero The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Interval Arithmetic – solving • Given bounds function f(x)=0, with interval I=[m, n] and tolerance SOLVE( m, n ) bounds = f([m, n]) If bounds [0, 1] return(false) else If width(bounds)< and m is a valid root return(true) else if SOLVE( m, (m+n)/2 ) return(true) else return(SOLVE( (m+n)/2, n ) ) The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Bounding Spheres • Two spheres overlap when: • c 2 and c 1 can be bounded ♦ their limits all three dimensions are known from the linearized equations of motion ♦ so solve using interval arithmetic The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Axis-Aligned Bounding Boxes • Can find AABBs that bound an object over an interval ♦ Linear motion of a vertex can be bounded by an AABB ♦ AABB of object is the combination of all vertex AABBs. • Use interval arithmetic to solve standard AABB test ♦ AABB bounds are the input The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Oriented Bounding Boxes “Fast Continuous Collision Detection Between Rigid Bodies” S. Redon, A. Kheddar, & S. Coquillart Eurographics 2002 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Oriented Bounding Boxes • Tighter fit than AABBs • Overlap test is based on concept of separating axes The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Oriented Bounding Boxes • What if the OBBs of objects are animated? • This is easy to do for rigid objects ♦ Apply the object’s transformation to the OBB ♦ Not the same as an OBB of the swept volume • The static OBB overlap tests are relatively straightforward equations ♦ They can be performed continuously as well! The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

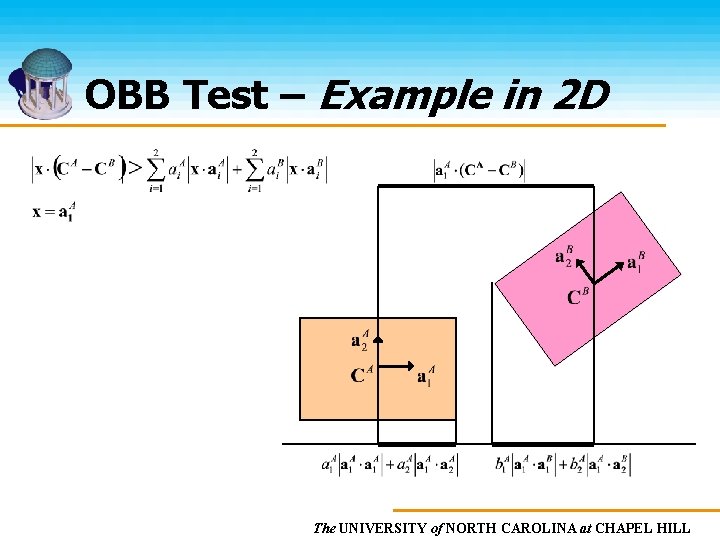
OBB Test • Define an OBB by three axes a 1, a 2, a 3, with half-sizes a 1, a 2, a 3, and center C • An axis, x, separates two OBBs, A and B, if and only if: • There are fifteen such axes • If all fifteen tests fail, then the OBBs overlap The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

OBB Test – Example in 2 D The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Continuous OBB Test • The separating axis values, ai, and C can be easily bounded. • So the separation equations can be computed with interval arithmetic. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Application - Cloth • Cloth simulation presents a particular challenge for both discrete and continuous collision detection “Interactive Collision Detection between Deformable Models using Chromatic Decomposition” - SIGGRAPH 2005 submission The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

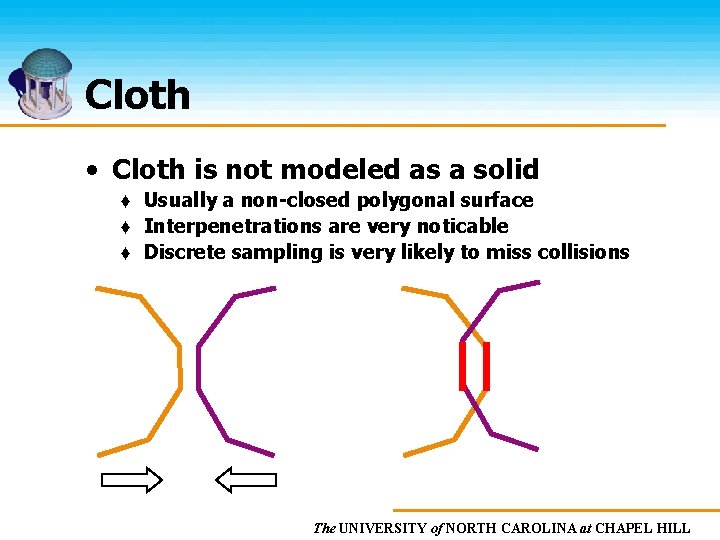
Cloth • Cloth is not modeled as a solid ♦ Usually a non-closed polygonal surface ♦ Interpenetrations are very noticable ♦ Discrete sampling is very likely to miss collisions The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Cloth • Cloth is highly deformable • Cloth may exhibit self-collision • Collision detection is the major bottleneck in cloth simulation The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Cloth CCD • Typical approach is AABB, followed by edge/edge and vertex/face CCD for all polygon pairs ♦ VERY expensive ♦ Potentially hundreds of millions of pairs • Swept volumes of polygonal primitives cannot be used ♦ Adjacent polygons will be false positives The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Our approach • Perform swept-volume CCD, but ensure that adjacent polygons are not checked • Accomplished through chromatic decomposition ♦ Divide the cloth into disjoint sets of polygons ♦ Check disjoint sets against each-other The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Our Approach • Swept-volume tests are GPU-accelerated • Exact triangle/triangle tests are done using interval arithmetic ♦ Number of required tests is greatly reduced The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Other Issues in CCD • Many collisions in close temporal proximity Small time steps ♦ Especially bad for real-time applications ♦ Can process groups of collisions that are known to be happening almost simultaneously The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Other Issues in CCD • Continuous and almost-continuous contact ♦ ♦ Resting/sliding motion Swept volumes and bounding volumes cannot help This is a problem in both discrete and continuous CD Such contacts need to be tracked separately The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL