Continuity Essential discontinuity Any other type of the

Continuity

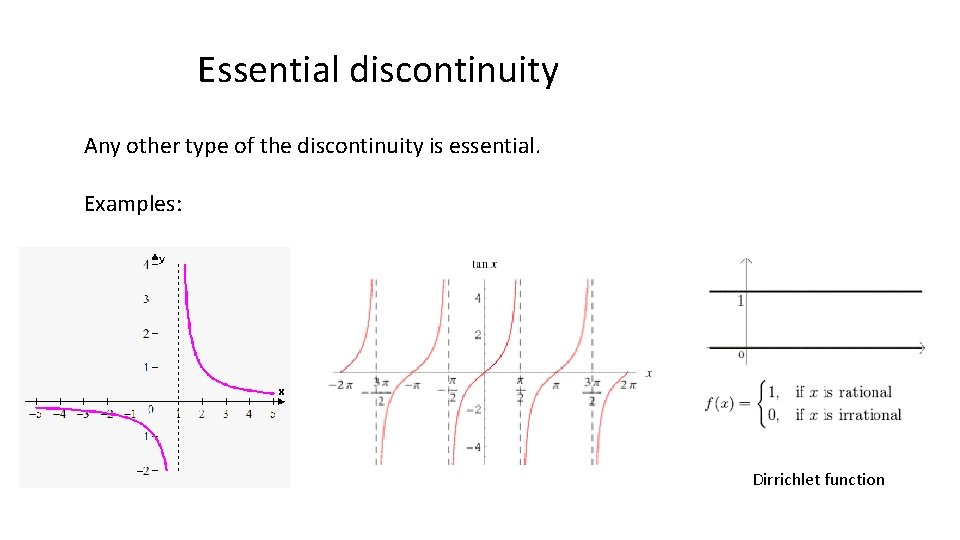
Essential discontinuity Any other type of the discontinuity is essential. Examples: Dirrichlet function

EXAMPLES Where discontinouos the given function? Give the type of the dicontinuity! Solution: x=0 and x=-3 isn’t element of the domain, so there the function discontinouos. At every other points the function continouos, because f(x) a ratio of two continouos functions.

x=4 also an essential discontinuity point. What is x=2, the anchor point? x=2 a jump point

Solution:

Continuity on an Interval • The function f is said to be continuous on an open interval (a, b) if – It is continuous at each number/point of the interval • It is said to be continuous on a closed interval [a, b] if – It is continuous at each number/point of the interval and – It is continuous from the right at a and continuous from the left at b 17

Intermediate Value Theorem If a function is continuous between a and b, then it takes on every value between and . Because the function is continuous, it must take on every y value between and.

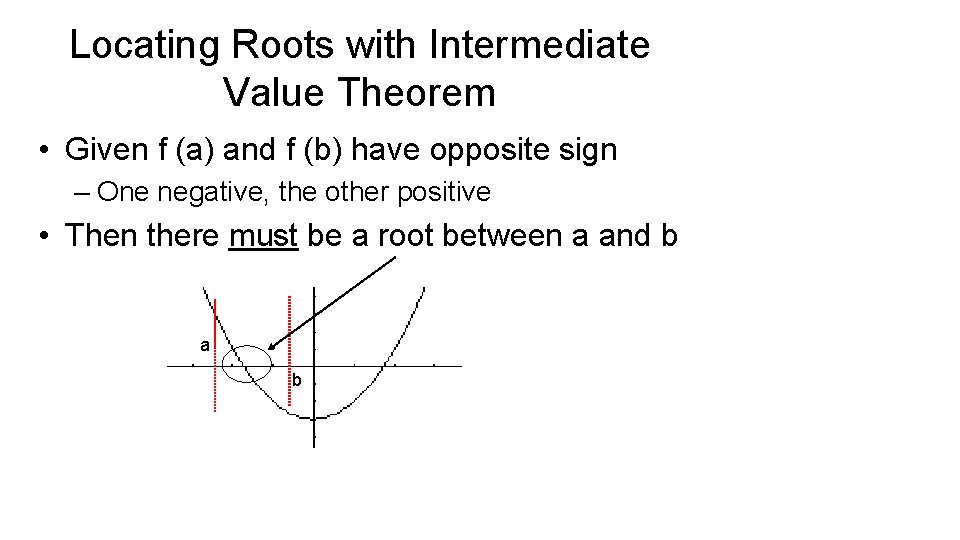
Locating Roots with Intermediate Value Theorem • Given f (a) and f (b) have opposite sign – One negative, the other positive • Then there must be a root between a and b a b

Intermediate value theorem, bounds. Intermediate value theorem: Given a continuous function in the interval [a, b], if f(a) and f(b) are of different signs, then there is at least one zero between a and b. f(3) = -9 f(4) = -7 f(5) = -3 f(6) = 3 There is a zero in the interval [5, 6] because there is a sign change, and by intermediate value theorem, a zero must exist in that interval.

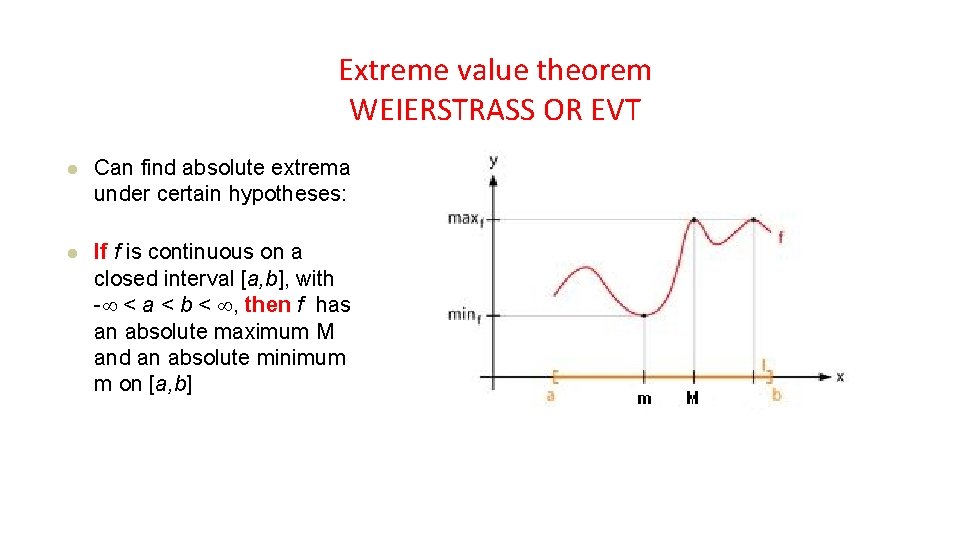
Extreme value theorem WEIERSTRASS OR EVT l Can find absolute extrema under certain hypotheses: l If f is continuous on a closed interval [a, b], with - < a < b < , then f has an absolute maximum M and an absolute minimum m on [a, b]

Example No maximum or minimum value on the domain. However, on [-3, 3], it has both. Question: does function f fullfil EVT?

Conclusions about hypotheses l l Conclude that hypothesis that interval be closed, [a, b], essential Conclusion that f is continuous also essential:

Examples fulfilling hypotheses l f(x) = 2 - 3 x where -5 < x < 8 l g(x) = sin(x) where 0 < x < 2 p

Limitations of Extreme Value Theorem l Polynomial f(x)=x 5 - 3 x 2 + 13 is continuous everywhere l Must have absolute max, min on [-1, 10] by theorem l Theorem doesn’t say where these occur l Extreme value theorem just an “existence theorem” l Learn tools for finding extrema later using the derivative

Derivative of a produce

Extension etc…

Derivative of a fraction

Derivative of the power function

Derivative of the power function

Solution:

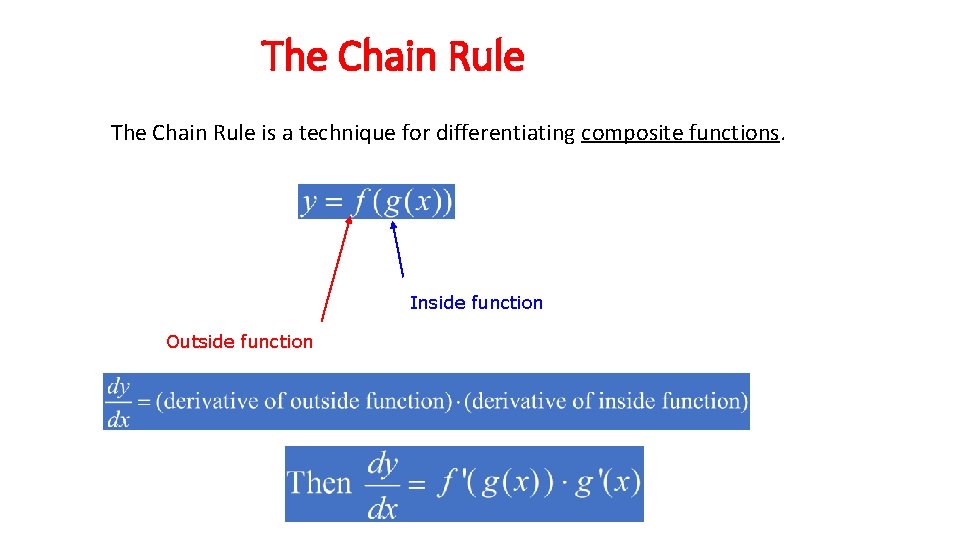
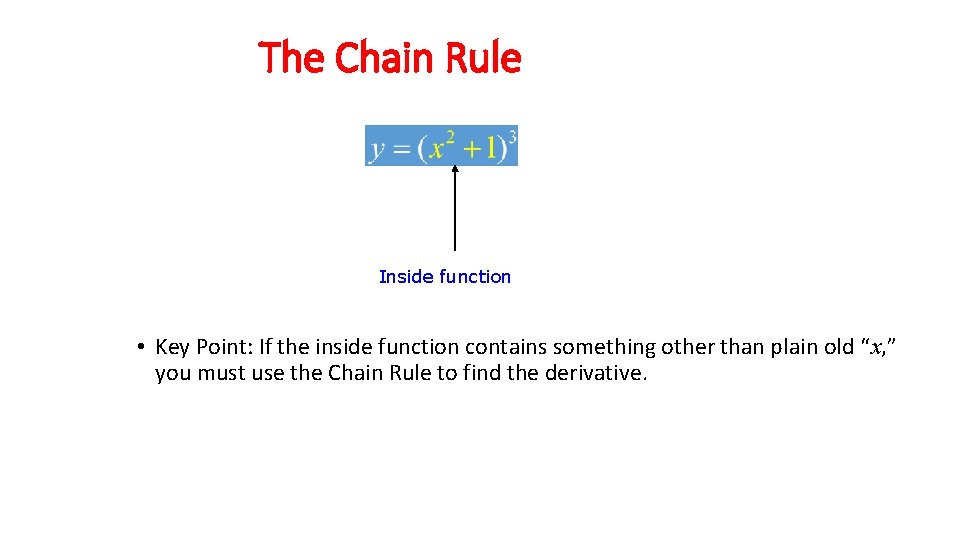
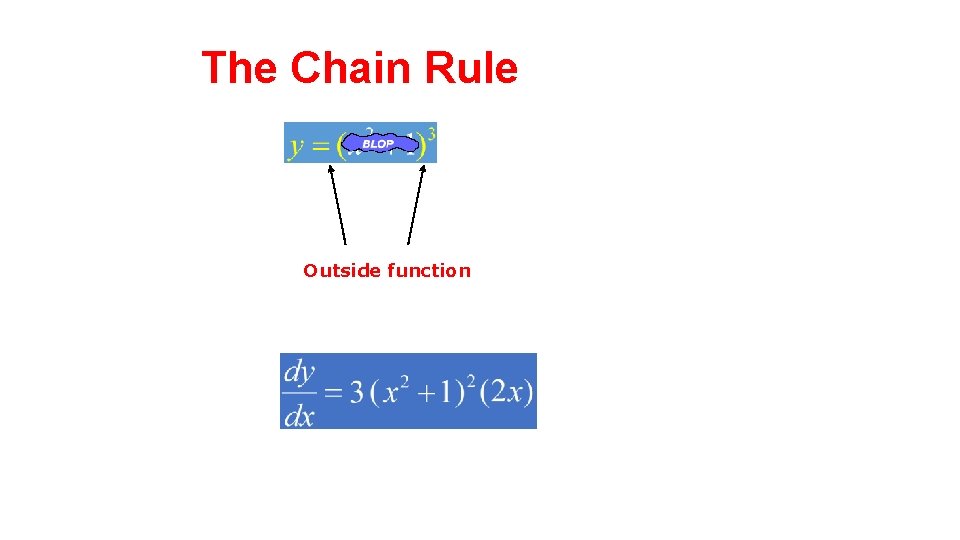
The Chain Rule is a technique for differentiating composite functions. Inside function Outside function

The Chain Rule 1. Identify inner and outer functions. 2. Derive outer function, leaving the inner function alone. 3. Derive the inner function.

The Chain Rule Inside function • Key Point: If the inside function contains something other than plain old “x, ” you must use the Chain Rule to find the derivative.

The Chain Rule Outside function

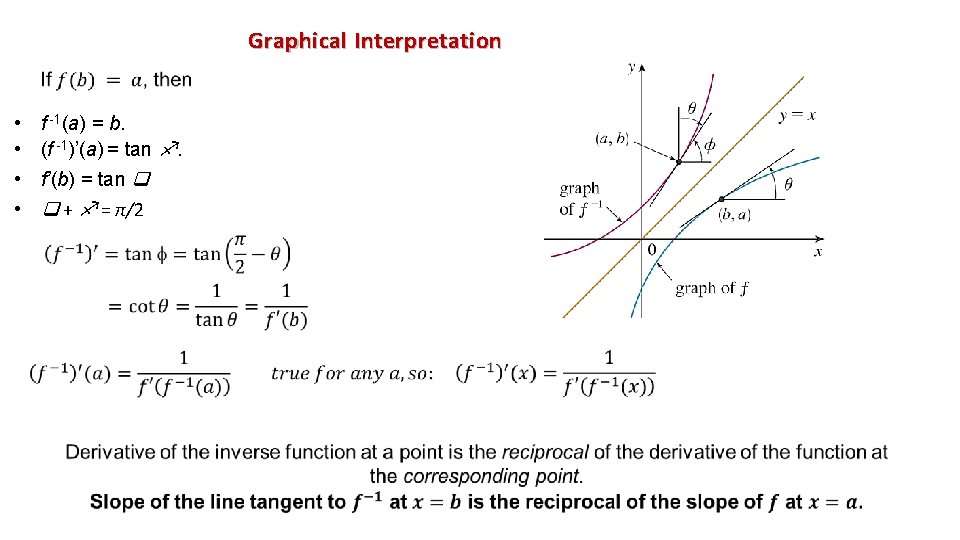
DERIVATIVE OF THE INVERSE FUNCTIONS

Graphical Interpretation • • f -1(a) = b. (f -1)’(a) = tan . f’(b) = tan + = π/2

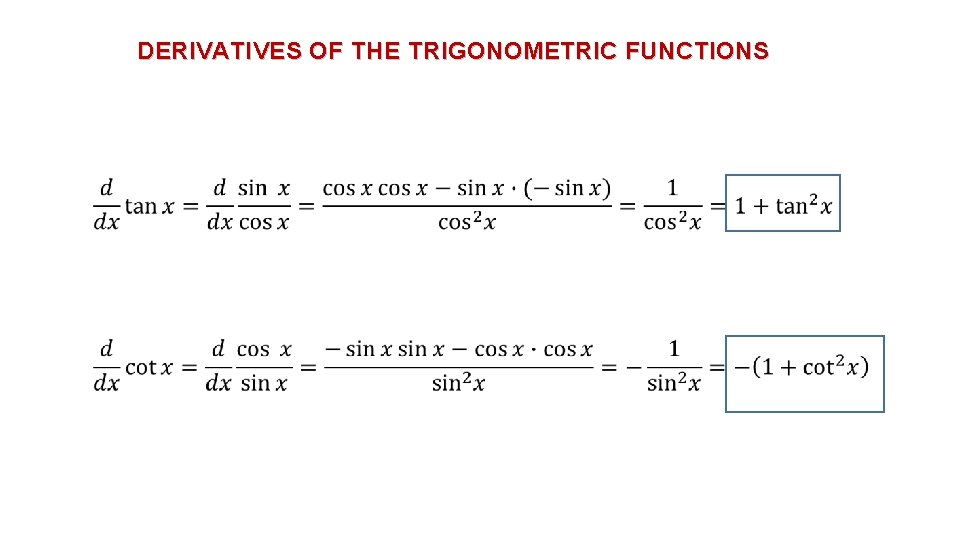
DERIVATIVES OF THE TRIGONOMETRIC FUNCTIONS

DERIVATIVES OF THE TRIGONOMETRIC FUNCTIONS

DERIVATIVES OF THE TRIGONOMETRIC FUNCTIONS

DERIVATIVES OF INVERSE TRIG ONOMETRIC FUNCTIONS

DERIVATIVES OF INVERSE TRIG FUNCTIONS

DERIVATIVE OF THE EXPONENTIAL FUNCTION

DERIVATIVE OF THE EXPONENTIAL FUNCTION

DERIVATIVE OF THE EXPONENTIAL FUNCTION

DERIVATIVE OF THE LOGARITHM FUNCTION

LOGARITHMIC DIFFERENTATION

LOGARITHMIC DIFFERENTATION example: