Continuit delle funzioni Funzione continua in un punto
















![Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-17.jpg)
![Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-18.jpg)
![Proprietà Se una funzione è continua in un intervallo chiuso [a, b], e se Proprietà Se una funzione è continua in un intervallo chiuso [a, b], e se](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-19.jpg)





![Dicesi funzione di funzione o funzione composta la funzione y=f[g(x)] Dicesi funzione di funzione o funzione composta la funzione y=f[g(x)]](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-25.jpg)
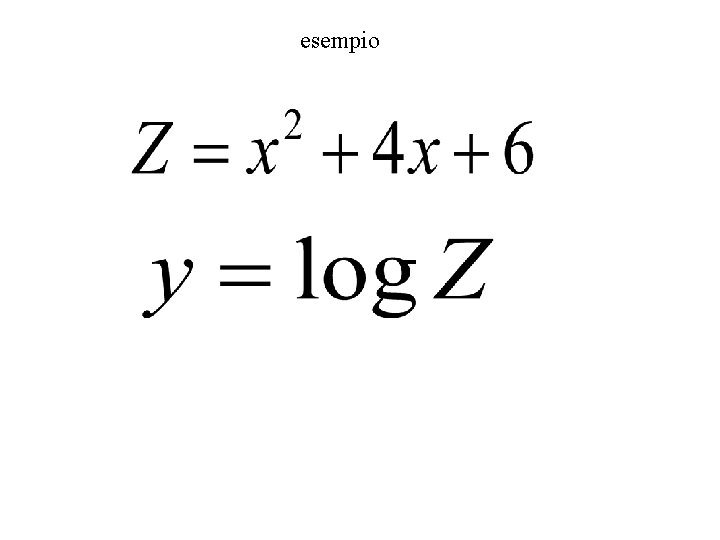
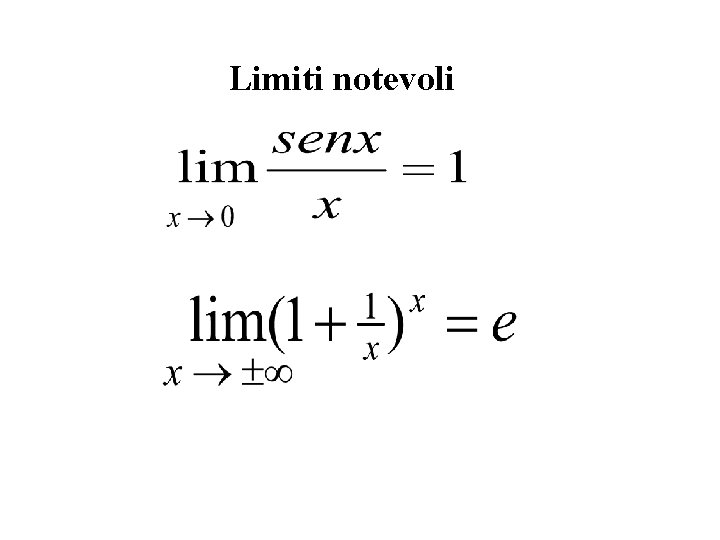











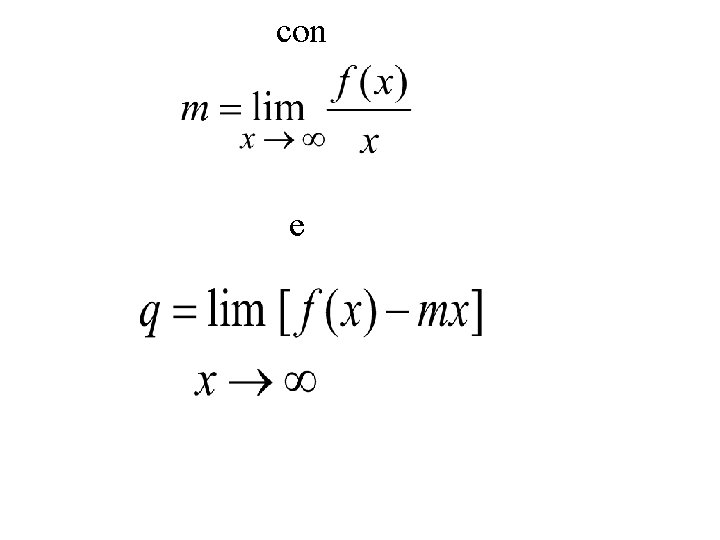










- Slides: 50

Continuità delle funzioni

Funzione continua in un punto Sia y=f(x) una funzione definita in un intervallo, aperto o chiuso, e sia x 0 un punto interno a questo intervallo; diciamo che la funzione f(x) è continua in x 0 se risulta: lim f(x) = f(x 0)

Deduzioni • Esiste il valore della funzione nel punto x 0 • Esiste ed è finito il limite della funzione per • Il limite coincide con il valore assunto dalla funzione nel punto

Se conveniamo di porre x = x 0 +h, con h variabile, la condizione di continuità si può esprimere nella forma: lim f(x 0 +h) = f(x 0)

Se una funzione f(x) è continua in un punto x 0 il calcolo del limite per x tendente a x 0 si ottiene ponendo nella funzione x = x 0

Esempi di funzioni continue a) La funzione f(x) = k è continua in ogni suo punto; cioè qualunque sia x 0 lim k = k

Esempi di funzioni continue b) La funzione f(x) = x è continua in ogni suo punto; cioè qualunque sia x 0 lim x = x 0

Esempi di funzioni continue c) La funzione f(x) = xn con n intero e positivo è continua in ogni suo punto; cioè qualunque sia x 0 lim xn =

Esempi di funzioni continue d) Se la funzione f(x) è continua in x 0 lo è pure la funzione k*f(x) con k costante; cioè

Esempi di funzioni continue e) Se le due funzioni f(x) e g(x) sono continue in x 0 lo sono pure: f(x) + g(x) f(x) - g(x) f(x) * g(x)

Esempi di funzioni continue f) La funzione razionale fratta è continua in ogni x che non annulla il denominatore

Esempi di funzioni continue f) La funzione f(x) = È continua in ogni x se n è un intero positivo dispari È continua in ogni x>0 se n è un intero positivo pari

Esempi di funzioni continue f) La funzione f(x) = è continua in ogni x (con a>0)

Esempi di funzioni continue f) La funzione f(x) = è continua in ogni x>0

Esempi di funzioni continue f) Le funzioni f(x) =senx e g(x)=cosx sono continue in ogni x

Funzione continua in un intervallo Una funzione è continua in un intervallo chiuso [a, b] se è continua in ogni punto dell’intervallo.
![Proprietà Se una funzione è continua in un intervallo chiuso a b essa assume Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-17.jpg)
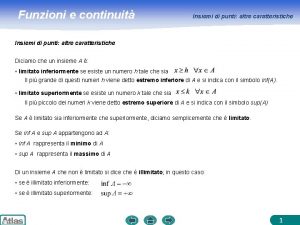
Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume nell’intervallo il massimo e il minimo assoluto. Teorema di Weirstrass
![Proprietà Se una funzione è continua in un intervallo chiuso a b essa assume Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-18.jpg)
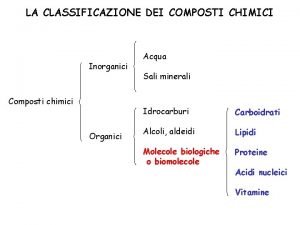
Proprietà Se una funzione è continua in un intervallo chiuso [a, b], essa assume nell’intervallo ogni valore compreso tra il suo minimo e massimo assoluti. Teorema di Bolzano
![Proprietà Se una funzione è continua in un intervallo chiuso a b e se Proprietà Se una funzione è continua in un intervallo chiuso [a, b], e se](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-19.jpg)
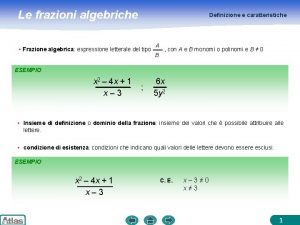
Proprietà Se una funzione è continua in un intervallo chiuso [a, b], e se agli estremi dell’intervallo assume valori di segno opposto, essa si annulla in almeno un punto interno all’intervallo. Teorema

Funzioni monotone Sia f(x) una funzione definita in un intervallo (a, b). Se per ogni coppia di punti x 1 e x 2 dell’intervallo, con x 1 < x 2 risulta: allora f(x) è crescente non decrescente non crescente M O N O T O N A

Funzioni limitate Sia f(x) una funzione definita in un intervallo (a, b). Se esiste un numero reale h tale che per ogni x dell’intervallo è f(x)<h allora f(x) è limitata superiormente Se esiste un numero reale k tale che per ogni x dell’intervallo è f(x)>k allora f(x) è limitata inferiormente I valori h e k possono non appartenere al codominio

Se h e k appartengono al codominio della funzione allora si chiamano minimo assoluto e massimo assoluto.

Funzione di funzione

Sia z=g(x) una funzione definita in un intervallo (a, b); Sia inoltre y=f(z) una funzione della variabile z, definita per ogni valore della variabile z che si ricava dalla funzione z=g(x) al variare di x nell’intervallo suddetto.
![Dicesi funzione di funzione o funzione composta la funzione yfgx Dicesi funzione di funzione o funzione composta la funzione y=f[g(x)]](https://slidetodoc.com/presentation_image/0e88de468b849215a6bf513ba49fbde7/image-25.jpg)
Dicesi funzione di funzione o funzione composta la funzione y=f[g(x)]
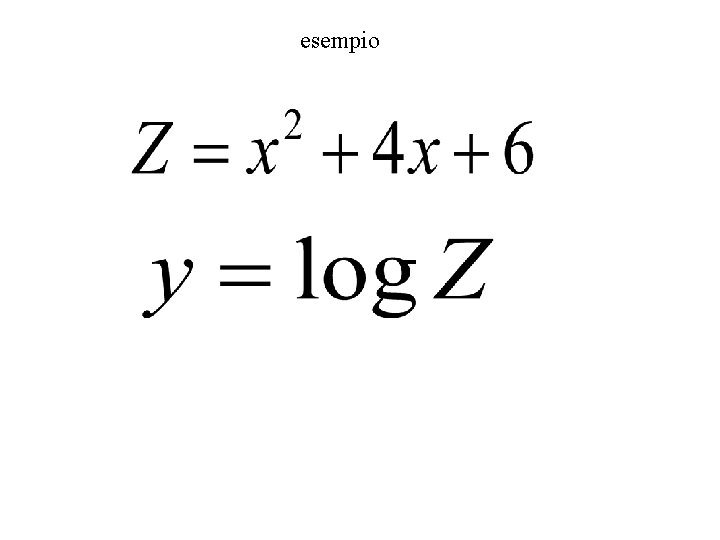
esempio

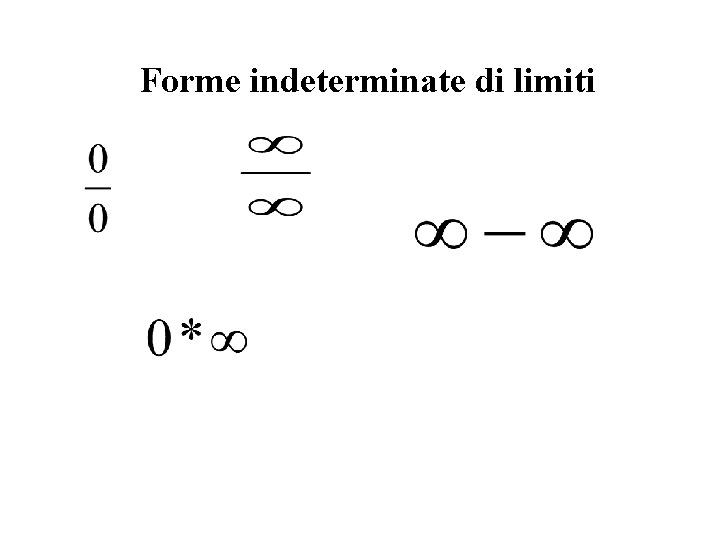
Forme indeterminate di limiti
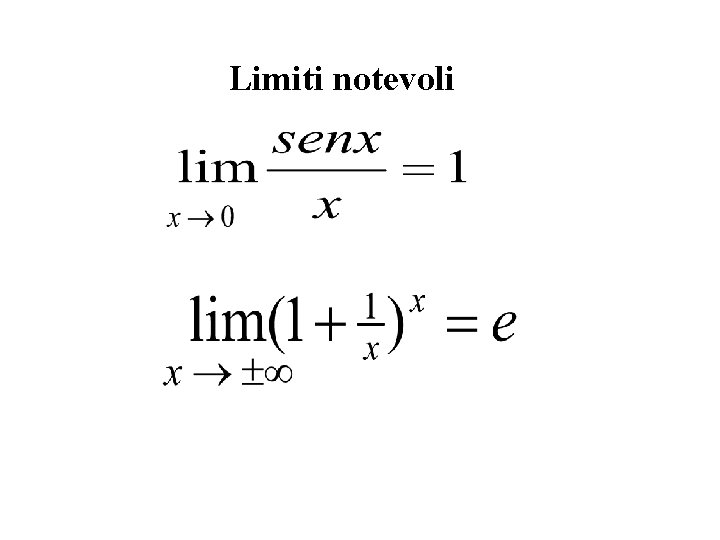
Limiti notevoli


Punti di discontinuità di una funzione

Discontinuità di prima specie La funzione è discontinua di prima specie in x 0 quando in tale punto esistono finiti e diversi il limite sinistro e destro.

La differenza Si chiama salto della funzione in x 0

Discontinuità di seconda specie La funzione è discontinua di seconda specie in x 0 quando in tale punto o non esiste o non è finito uno dei limiti sinistro e destro. .

Discontinuità di terza specie La funzione è discontinua di terza specie in x 0 quando in tale punto esiste finito ma la f(x) non è definita in tale punto o il suo valore è diverso da detto limite.

La discontinuità di terza specie è eliminabile perché si può sostituire ad f(x 0 ) il valore del limite.

esempi

Asintoti La retta x=x 0 si dice asintoto verticale della funzione y=f(x) se: oppure

Asintoti La retta y=l si dice asintoto orizzontale della funzione y=f(x) se:

Asintoti La retta y=mx+q si dice asintoto obliquo della funzione y=f(x) se:
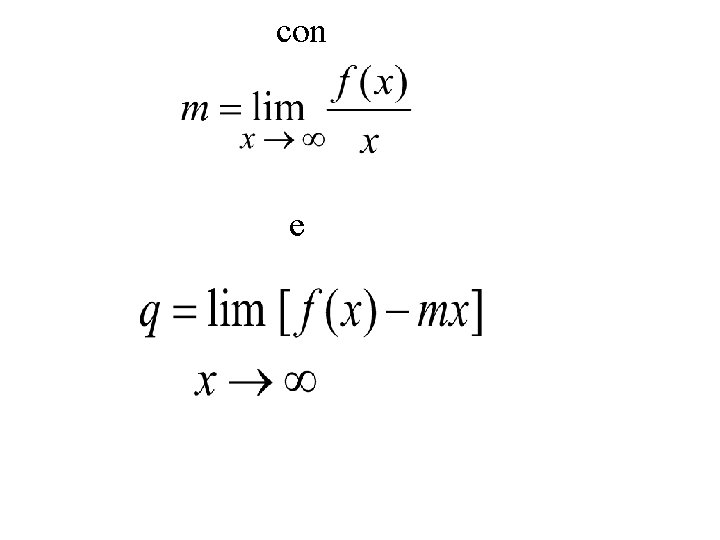
con e

Infinitesimi Una funzione f(x) si dice infinitesimo per x che tende a x 0 se:

Se f(x) e g(x) sono infinitesimi per x che tende a x 0 e se esiste un intorno di tale punto tale che in tutti i punti dell’intorno risulti g(x) diverso da zero allora si potrà avere:

f(x) è un infinitesimo di ordine superiore a g(x); cioè tende a zero più velocemente.

f(x) è un infinitesimo di ordine inferiore a g(x); cioè tende a zero meno velocemente.

f(x) è un infinitesimo dello stesso ordine di g(x); cioè tende a zero con la stessa velocità.

f(x) e g(x) non sono confrontabili.

Per confrontare più infinitesimi spesso si fa riferimento ad un medesimo infinitesimo chiamato infinitesimo principale che sarà:

f(x) è un infinitesimo di ordine n rispetto all’infinitesimo principale se:

Infinito Una funzione f(x) si dice infinito per x che tende a x 0 se:

Infiniti
 Funzione
Funzione Teoremi sulle funzioni continue
Teoremi sulle funzioni continue Teorema degli zeri
Teorema degli zeri Funzione delle proteine
Funzione delle proteine Grafici funzioni goniometriche esercizi
Grafici funzioni goniometriche esercizi Estremanti di una funzione
Estremanti di una funzione Dilatazione trasformazione geometrica
Dilatazione trasformazione geometrica Opanoidi
Opanoidi Definizione di limite
Definizione di limite Funzioni dei carboidrati
Funzioni dei carboidrati Slidetodoc.com
Slidetodoc.com Método punto por punto
Método punto por punto Rete punto punto
Rete punto punto Punto iv
Punto iv Cuando se usa una coma
Cuando se usa una coma Rete punto a punto
Rete punto a punto Punto di intersezione delle mediane
Punto di intersezione delle mediane L'esperienzia delle cose moderne e la lezione delle antique
L'esperienzia delle cose moderne e la lezione delle antique La nascita delle lingue e delle letterature romanze
La nascita delle lingue e delle letterature romanze L esperienza delle cose moderne e la lezione delle antique
L esperienza delle cose moderne e la lezione delle antique Disequazione esponenziale
Disequazione esponenziale Problemi cognitivi
Problemi cognitivi Funzioni a due variabili
Funzioni a due variabili Le funzioni della lingua
Le funzioni della lingua Minterm
Minterm Ruoli e funzioni aziendali
Ruoli e funzioni aziendali Bulbo ponte
Bulbo ponte Funzioni vitali esseri viventi
Funzioni vitali esseri viventi Gli elementi della fiaba
Gli elementi della fiaba Schema di jakobson spiegazione
Schema di jakobson spiegazione Le proteine funzioni
Le proteine funzioni Funzioni del sistema finanziario
Funzioni del sistema finanziario Cosa sono i principi nutritivi
Cosa sono i principi nutritivi Grafici funzioni
Grafici funzioni Spazi e funzioni della casa
Spazi e funzioni della casa Introduzione alle funzioni
Introduzione alle funzioni Funzioni della moneta
Funzioni della moneta Che cosa è il metodo augustus?
Che cosa è il metodo augustus? Definizione frazione
Definizione frazione Formule trigonometria
Formule trigonometria Funzioni in c
Funzioni in c Studio di funzioni
Studio di funzioni Requirente
Requirente Funzioni lineari
Funzioni lineari Robot curiosity funzioni
Robot curiosity funzioni Poqe
Poqe L'intersezione con il piano oyz è la circonferenza
L'intersezione con il piano oyz è la circonferenza Funzioni reali di due variabili reali
Funzioni reali di due variabili reali F(x) = senx
F(x) = senx Logaritmi zanichelli
Logaritmi zanichelli Circolo portale ipotalamo ipofisario
Circolo portale ipotalamo ipofisario