Continued Fractions Euclidean Algorithm and Lehmers Algorithm Applied

Continued Fractions, Euclidean Algorithm and Lehmer’s Algorithm Applied Symbolic Computation CS 567 Jeremy Johnson

Outline Fast Fibonacci Continued Fractions Lehmer’s Algorithm Analysis of the Euclidean Algorithm (bit complexity) • Assignment 1 • •

Euclidean Algorithm g = gcd(a, b) a 1 = a; a 2 = b; while (a 2 0) a 3 = a 1 mod a 2; a 1 = a 2; a 2 = a 3; } return a 1;

Remainder Sequence a 1 = a, a 2 = b a 1 = q 3 a 2 + a 3, 0 a 3 < a 2 ai = qi ai+1 + ai+2, 0 ai+2 < ai+1 al= ql al+1 gcd(a, b) = a l+1

Extended Euclidean Algorithm g = gcd(a, b, *x, *y) a 1 = a; a 2 = b; x 1 = 1; x 2 = 0; y 1 = 0; y 2 = 1; while (a 2 0) a 3 = a 1 mod a 2; q = floor(a 1/a 2); x 3 = x 1 – q*x 2; y 3 = y 1 – q*y 2; a 1 = a 2; a 2 = a 3; x 1 = x 2; x 2 = x 3; y 1 = y 2; y 2 = y 3; } return a 1;

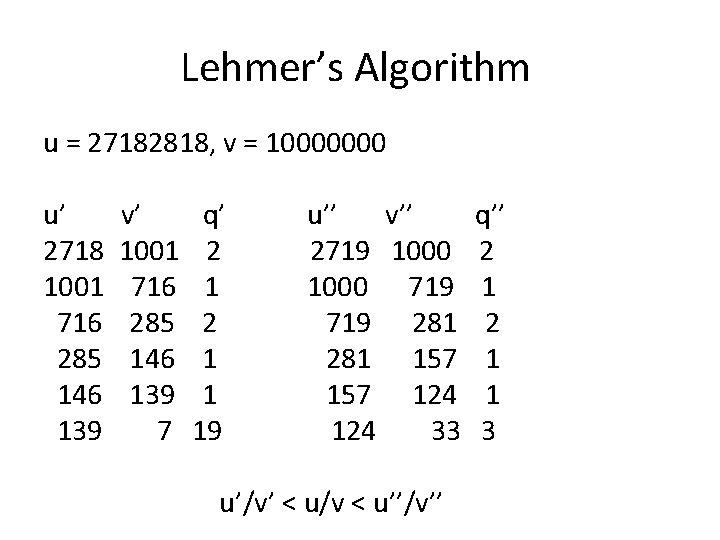
Lehmer’s Algorithm u = 27182818, v = 10000000 u’ 2718 1001 716 285 146 139 v’ 1001 716 285 146 139 7 q’ 2 1 1 19 u’’ v’’ 2719 1000 719 281 157 124 33 u’/v’ < u/v < u’’/v’’ q’’ 2 1 1 3

Maximum Number of Divisions Theorem. Let a b 0 and n = number of divisions required by the Euclidean algorithm to compute gcd(a, b). Then n < 2 lg(a).

Maximum Number of Divisions Theorem. The smallest pair of integers that require n divisions to compute their gcd is F and F n+1. n+2 Theorem. Let a b 0 and n = number of divisions required by the Euclidean algorithm to compute gcd(a, b). Then n < 1. 44 lg(a).

Average Number of Divisions Theorem. Let a b 0 and n = average number of divisions required by the Euclidean algorithm to compute gcd(a, b). Then n 12 ln(2) 2/ 2 lg(a) 0. 584 lg(a). Theorem [Dixon] D(a, b) ½ ln(a) for almost all pairs u a b 1 as u

Dominance and Codominance Definition. Let f, g be real valued functions on a common set S. • [Dominance] • [Codominance] • [Strict Dominance]

Basic Properties Theorem. Let f, f 1, f 2, g, g 1, and g 2 be nonnegative real-valued functions on S and c>0.

Integer Length Definition. A = i=0. . m ai i, L (A) = m • •

Basic Arithmetic Computing Times Theorem. Let A, M, D be the classical algorithms for addition, multiplication and division.

Maximum Computing Time Theorem.

Average Computing Time Theorem.

Probability of Relative Primality p/d 2 = 1 p = 1/ (2) (z) = 1/n z (2) = 2/6

Formal Proof Let q n be the number of 1 a, b n such that gcd(a, b) = 1. Then lim n qn/n 2 = 6/ 2

Mobius Function • (1) = 1 • (p 1 pt) = -1 t • (n) = 0 if p 2|n (ab) = (a) (b) if gcd(a, b) = 1.

Mobius Inversion d|n (d) = 0 ( n (n)n s) ( n 1/n s) = 1

Formal Proof qn = n (k) n/k 2 lim n qn/n 2 = n (n)/n 2 = 1/( n 1/n 2) = 6/ 2

Assignment 1 • Empirically investigate distribution of quotients in Euclidean algorithm • Implement and analyze classical division algorithm • Implement and analyze Lehmer’s algorithm • Study and summarize gcd algorithms in GMP