Contextfree Grammars Adapted from material by Prof Alex

Context-free Grammars Adapted from material by: Prof. Alex Aiken and Prof. George Necula (UCB) CS 780(Prasad) L 6 CFG 1

Outline ØRegular languages revisited ØParser overview ØContext-free grammars (CFGs) ØDerivations ØAmbiguity CS 780(Prasad) L 6 CFG 2

Regularity • Languages requiring counting modulo a fixed number are regular. • Finite automaton cannot count without limit or remember number of times it has visited a particular state. • Many languages are not regular. E. g. , Language of balanced parentheses is not regular. CS 780(Prasad) L 6 CFG 3

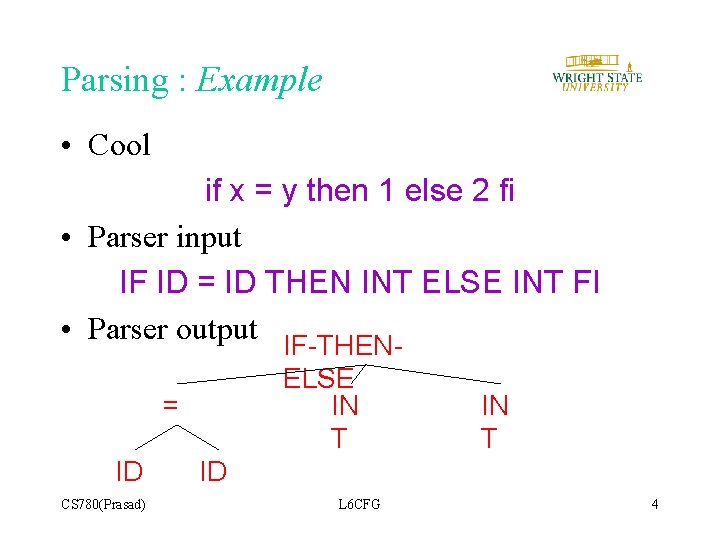
Parsing : Example • Cool if x = y then 1 else 2 fi • Parser input IF ID = ID THEN INT ELSE INT FI • Parser output IF-THENELSE IN T = ID CS 780(Prasad) IN T ID L 6 CFG 4

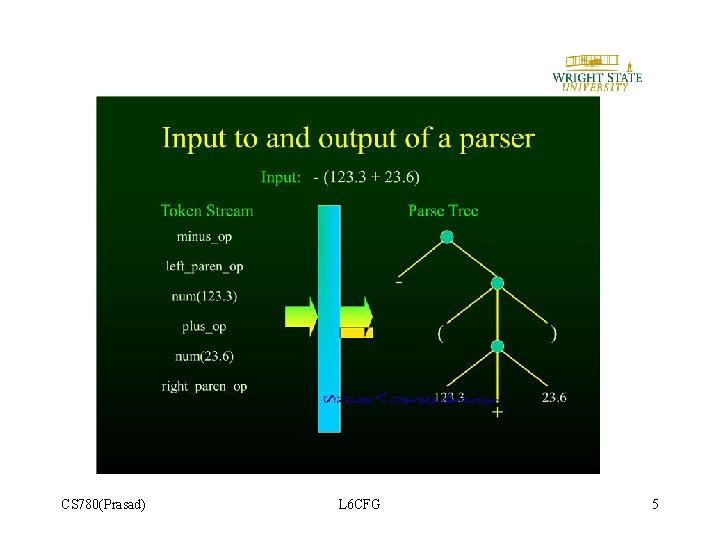
CS 780(Prasad) L 6 CFG 5

Context-Free Grammars • Programming language constructs have recursive structure. ØAn EXPR is if EXPR then EXPR else EXPR fi while EXPR loop EXPR pool … • Context-free grammars are a natural notation for this recursive structure. q. Iteration : Regular Expression q. Tail Recursion : Regular Grammar q. General Recursion : Context-free Grammar CS 780(Prasad) L 6 CFG 6

CFG = (N, T, P, S) • • N : Finite set of variables/non-terminals T : Alphabet/Finite set of terminals P : Finite set of rules/productions S : Start symbol CS 780(Prasad) L 6 CFG 7

• a* represents a context-free language because we can write a CFG for it. • Context-freeness: An A-rule can be applied whenever A occurs in a string, irrespective of the context (that is, non-terminals and terminals around A). q. Cf. context-sensitive grammar (“declare-use”) CS 780(Prasad) L 6 CFG 8

Examples of CFGs • A fragment of Cool: –Non-terminals are written in upper-case. –Terminals are in lower-case. –The start symbol is the left-hand side of the first production. CS 780(Prasad) L 6 CFG 9

• Balanced Parenthesis Grammar S (S)S | ε • Simple arithmetic expressions: CS 780(Prasad) L 6 CFG 10

CS 780(Prasad) L 6 CFG 11

From CFG to Language • One-step Derivation • w is derivable from v in CFG, if there is a finite sequence of rule applications such that: CS 780(Prasad) L 6 CFG 12

Let G=(N, T, P, S) be a CFG. • is a sentential form, if. • is a sentence, if. • The language of G, L(G) = CS 780(Prasad) L 6 CFG 13

Cool Example • Some “terminal strings” in the Cool language. CS 780(Prasad) L 6 CFG 14

Notes on Parser • Parser checks the membership in a language + constructs a parse tree for the input. • Parser must handle errors gracefully. • Parser generators implement CFG’s (e. g. , bison). • Form of the grammar is important. ØMany grammars generate the same language. ØTools are sensitive to the form of the grammar. CS 780(Prasad) L 6 CFG 15

Derivations and Parse Trees • A derivation is a sequence of production applications. • A derivation can be drawn as a tree ØStart symbol is the tree’s root ØFor a production add children to (parent) node CS 780(Prasad) L 6 CFG 16

Derivation Example • Grammar • String CS 780(Prasad) L 6 CFG 17

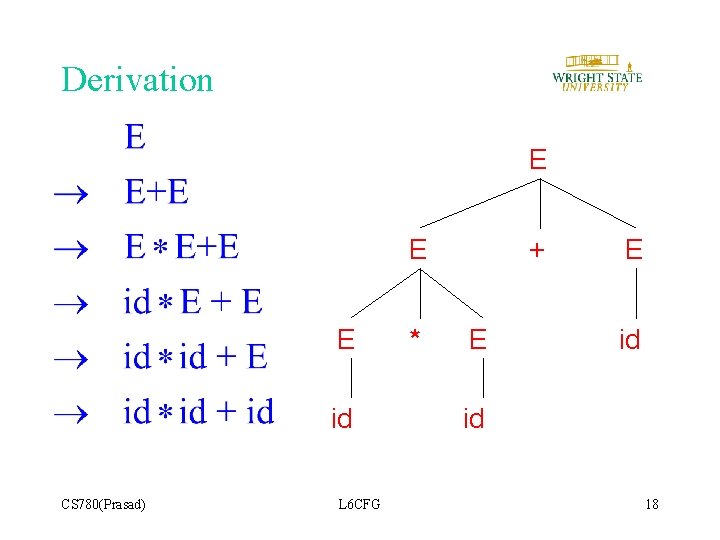
Derivation E E E id CS 780(Prasad) L 6 CFG * + E E id id 18

Derivation in Detail (1) E CS 780(Prasad) L 6 CFG 19

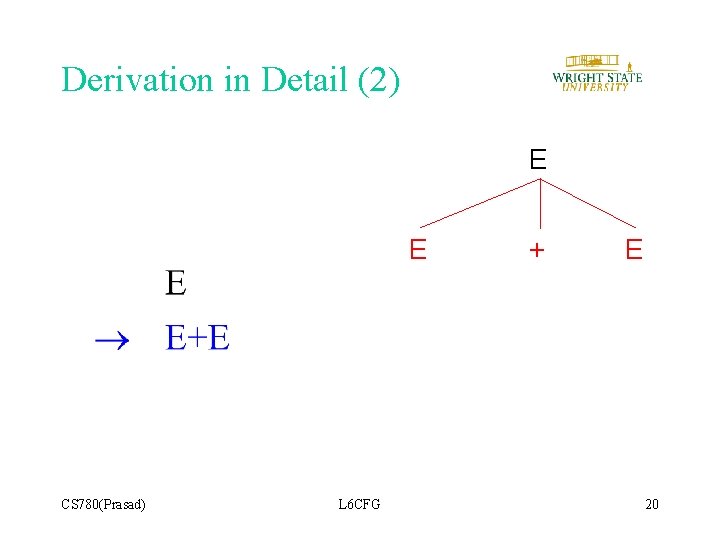
Derivation in Detail (2) E E CS 780(Prasad) L 6 CFG + E 20

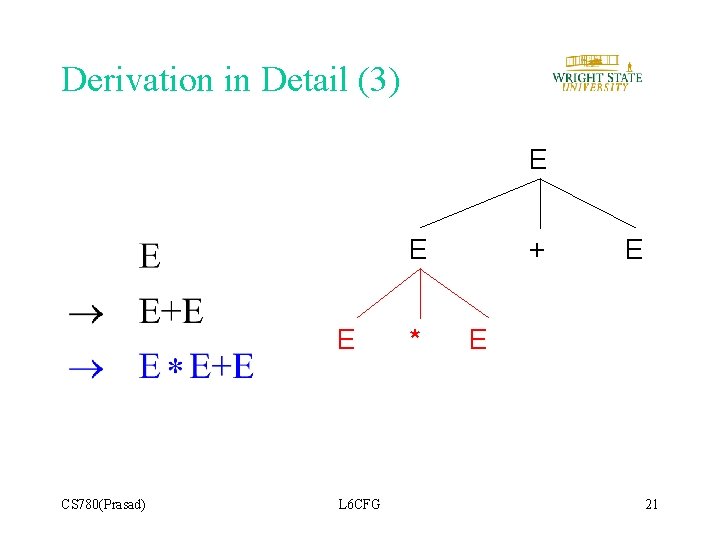
Derivation in Detail (3) E E E CS 780(Prasad) L 6 CFG * + E E 21

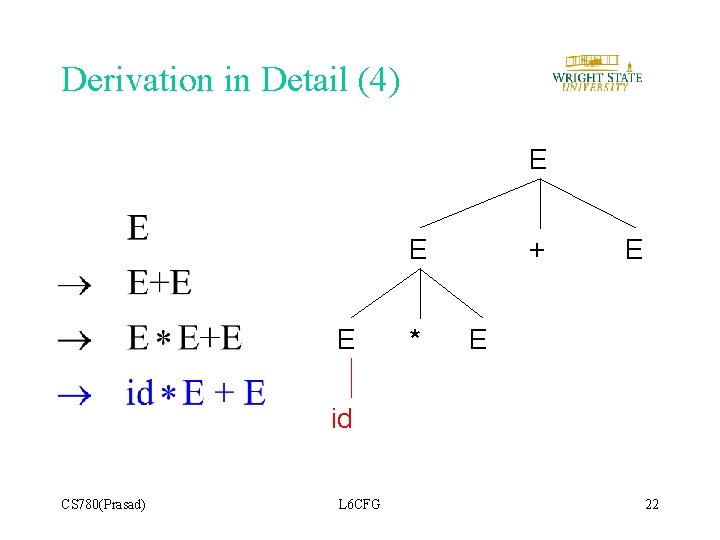
Derivation in Detail (4) E E E * + E E id CS 780(Prasad) L 6 CFG 22

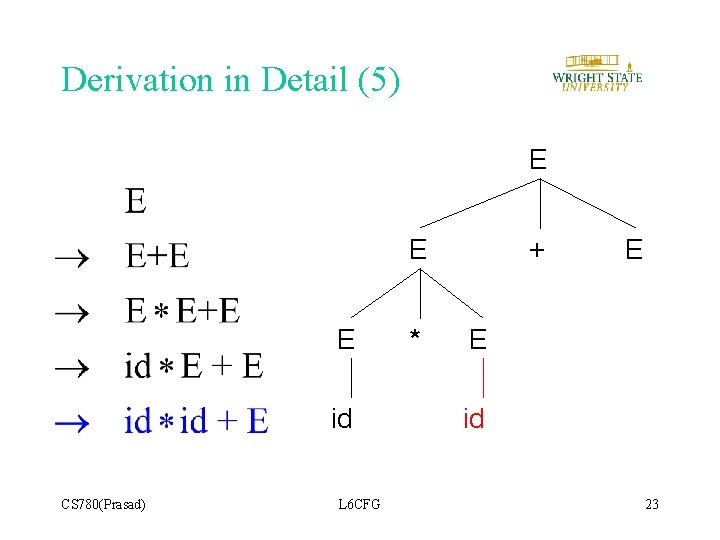
Derivation in Detail (5) E E E id CS 780(Prasad) L 6 CFG * + E E id 23

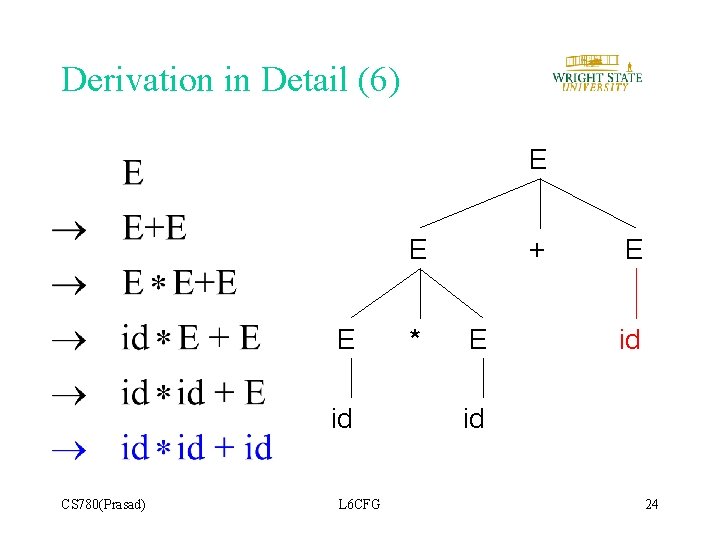
Derivation in Detail (6) E E E id CS 780(Prasad) L 6 CFG * + E E id id 24

Notes on Derivations • A parse tree has ØTerminals at the leaves. ØNon-terminals at the interior nodes. • An in-order traversal of the leaves is the original input. • The parse tree shows the association of operations, the input string does not. CS 780(Prasad) L 6 CFG 25

Left-most and Right-most Derivations • The previous example is a left-most derivation. Ø At each step, replace the left-most nonterminal. • There is an equivalent notion of a right-most derivation. CS 780(Prasad) L 6 CFG 26

Right-most Derivation in Detail (1) E CS 780(Prasad) L 6 CFG 27

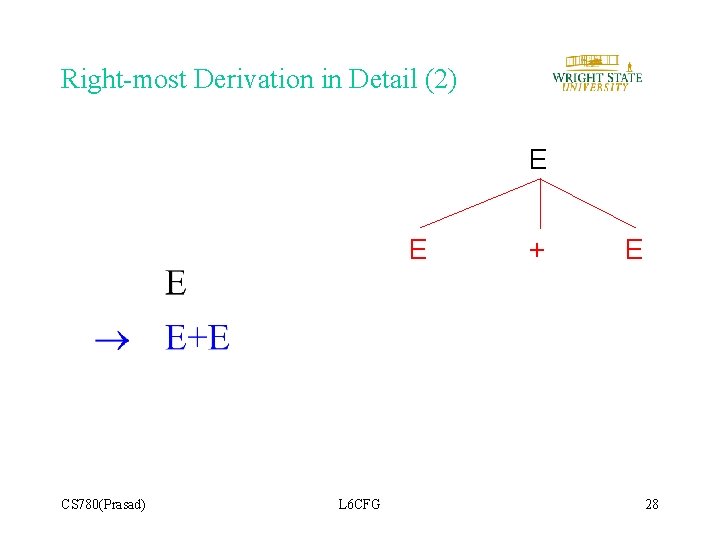
Right-most Derivation in Detail (2) E E CS 780(Prasad) L 6 CFG + E 28

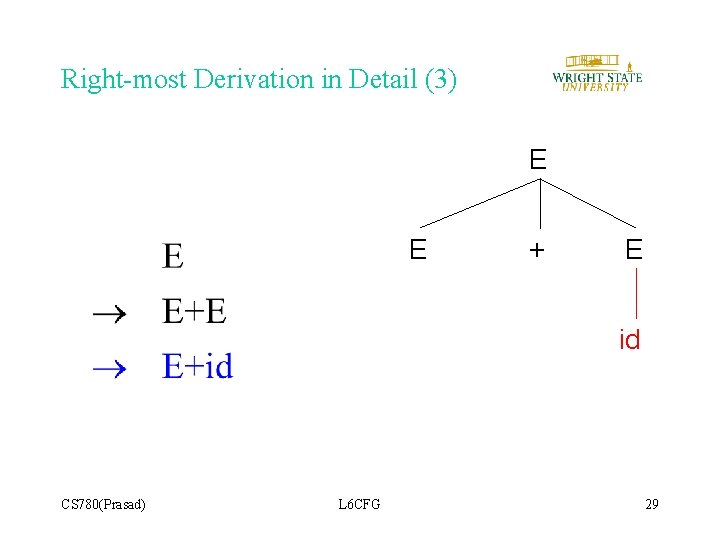
Right-most Derivation in Detail (3) E E + E id CS 780(Prasad) L 6 CFG 29

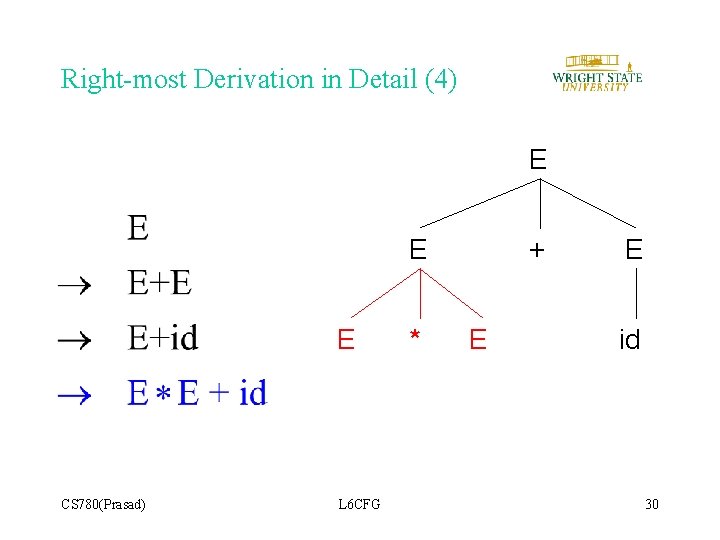
Right-most Derivation in Detail (4) E E E CS 780(Prasad) L 6 CFG * + E E id 30

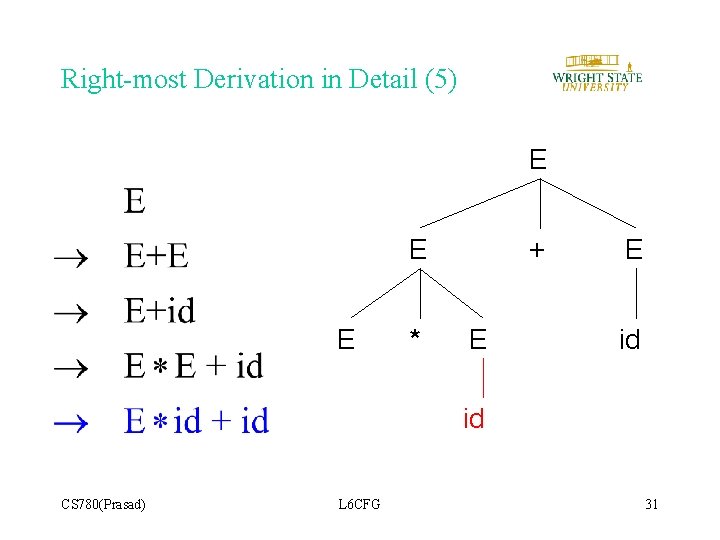
Right-most Derivation in Detail (5) E E E * + E E id id CS 780(Prasad) L 6 CFG 31

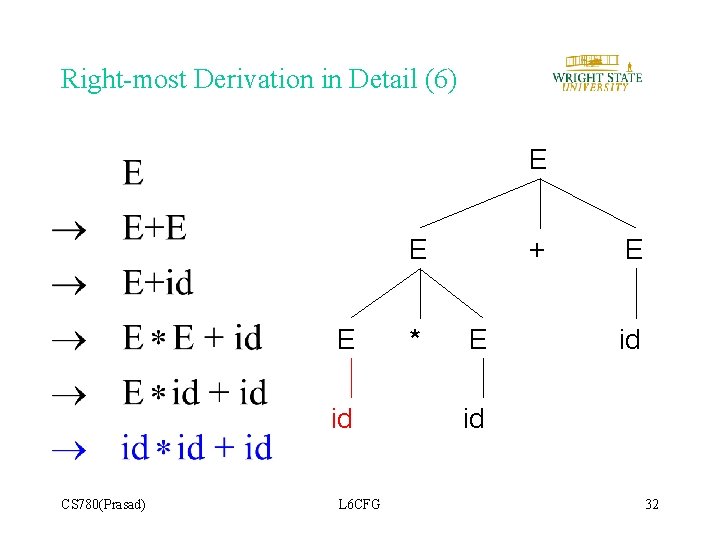
Right-most Derivation in Detail (6) E E E id CS 780(Prasad) L 6 CFG * + E E id id 32

Summary of Derivations • Note that right-most and left-most derivations have the same parse tree; the difference is the order in which the branches are added. • We are not just interested in whether s e L(G) Ø We need a parse tree for s. • A derivation defines a parse tree, but one parse tree may have many associated derivations. • Left-most and right-most derivations are important in parser implementation. CS 780(Prasad) L 6 CFG 33

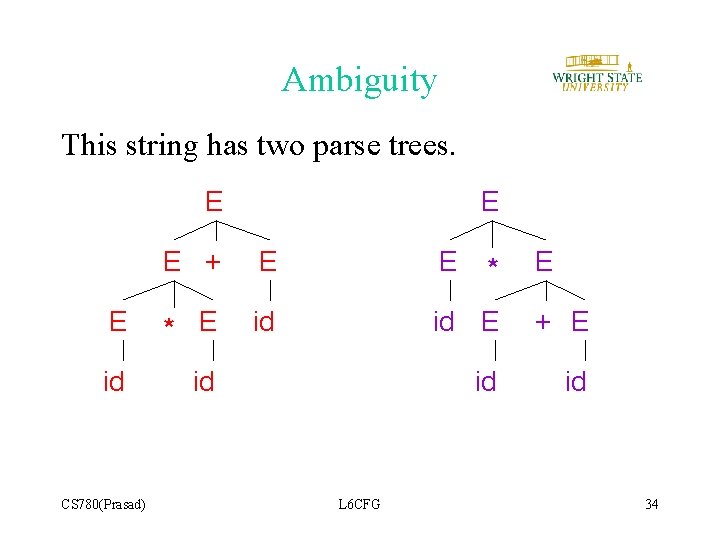
Ambiguity This string has two parse trees. E E E + E E E * E id id E + E id id CS 780(Prasad) L 6 CFG * E 34

• A grammar is ambiguous if it has more than one parse tree for a string. • Ambiguity is BAD because it leaves meaning of some programs ill-defined. • Ambiguity can be avoided by rewriting the grammar. ØInterprets non-fully parenthesized expression, giving precedence to * over +. CS 780(Prasad) L 6 CFG 35