Context Free Grammars CHAPTER 12 Compiler A compiler

Context Free Grammars CHAPTER 12

Compiler: A compiler is program that converts a high level language code into its equivalent assembly language. Grammar: Grammar is a set of rules by which a valid sentence in a language is constructed. Parsing the sentence: Parsing is the process of analyzing a text, made of a sequence of tokens (e. g. words), to determine its grammatical structure with respect to a given formal grammar. 2

Semantics: The grammatical rules which involve the meaning of words are called Semantics e. g. in English language, the sentence “Buildings sing” make no sense. Syntactics: The grammatical rules that don’t involve the meaning of the words but the structure of the words. Context Free Grammar (CFG): general definition A grammar or language based on rules that describe a change in the string without reference to elements not in the string. The concept of CFG was introduce by the linguist Noam Chomsky in 1956. 3

Terminals: CFG Terminology: The symbols that cannot be replaced by anything are called terminals. Non-Terminals: The symbols that must be replaced by other things are called nonterminals. e. g. variable = expr; Derivation: The sequence of application of the rules that produces the finished string of terminal from the starting symbol is called a derivation. Productions: The grammatical rules are often called productions. 4

Context Free Grammar (CFG): technical definition A CFG is a collection of three things; 1. An alphabet of letters called terminal, from which strings or words of the language are formed. 2. A set of symbols called non-terminals, one of which is the symbol S, standing for : start here”. 3. A finite set of productions of the form One non-terminal finite string of terminals and /or non-terminals 5

Context Free Grammars By definition a context-free grammar is a finite set of variables (also called non-terminals or syntactic categories - synonym for "variable") each of which represents a language. The languages represented by the variables are described recursively in terms of each other and primitive symbols called terminals. The rules relating the variables are called productions.

Context Free Grammars Example ◦ S → a. S ◦S→Λ ◦ Continuous strings of as Strings with at least one double letter ◦ S → ADA ◦ A → a. A ◦ A → b. A ◦A→Λ ◦ D → aa ◦ D → bb

Example S a. A | b. X A b. A X c. X

Context Free Language (CFL): The language generated by CFG is called context Free Language (CFL). Note: CFG can generate all regular languages and some non-regular languages, but not all the non-regular languages. Examples: 9

Context Free Grammars A context-free grammar, is a collection of three things ◦ An alphabet of letters called terminals from which strings of language are generated ◦ A set of symbols called nonterminals, one of which is a symbol S, termed as the start symbol ◦ A finite set of productions (production rules) of the form ◦ One nonterminal Finite string of Terminals and / or Nonterminals The strings of terminals and nonterminals can consist of only terminals or of only nonterminals, or of any mixture of terminals and nonterminals or even the empty string A CFG must has at least one production that has the nonterminal S at its left side

Context Free Grammars Nonterminal / Variables / Syntactic category ◦ A symbol that can be substituted by some other symbol(s) ◦ Variable because the same non-terminal can have multiple substitutions Terminal ◦ A symbol that cannot be substituted further ◦ Letters from the alphabet set

Context Free Grammars Conventions for CFG ◦ Nonterminals are written in upper case letters ◦ Terminals Symbols are written in lower case Terminal symbols are also called atomic symbols

Context Free Grammars Terminologies ◦ Generation or Derivation ◦ The sequence of applications of the rules that produces the finished string of terminals from the starting symbol is called a generation or a derivation of the word ◦ Production ◦ The grammatical rules are called productions

Context Free Languages The language generated by a CFG is the set of all strings of terminals that can be produced from the start symbol S using the productions as substitutions. A language generated by a CFG is called a Context Free Language (CFL)

Context Free Grammars Non terminals vs. terminals ◦ ◦ ◦ ◦ S→X S→Y X→Λ Y → a. Y Y → b. Y Y→a Y→b

Context Free Grammars S → Xaa. X X → b. X X→Λ (a+b)* aa (a+b)*

CFG Examples ◦ All strings that don’t end at ba ◦ All strings that contain the substring “bbb” ◦ All strings that start and end with different letters

CFG Which languages do these CFGs define ◦ S → ab. S ◦ S → ab ◦ S → a. S ◦ S → bb

Context Free Grammars CFG For L = {anbn n 0 1 2 3 4 …} ◦ S → a. Sb ◦ S→Λ ◦ S → ab CFG For EQUAL ◦ ◦ ◦ ◦ S → a. B S → b. A A→a A → a. S A → b. AA B→b B → b. S B → a. BB

Context Free Grammars CFG For EQUAL ◦ ◦ ◦ ◦ S → a. B S → b. A A→a A → a. S A → b. AA B→b B → b. S B → a. BB Can be compactly written as S → a. B | b. A A → a | a. S | b. AA B → b | b. S | Abb <S> : : = a<B> | b<A> <A >: : = a | a<S> | b<A><A> <B> : : = b | b<S> | <A>bb

Backus-Naur Form This format for writing a CFG is called Backus-Naur Form It is abbreviated as BNF Also called Backus Normal Form Consist of arrows to define production Vertical Bars to present choices (disjunction) Terminals and non Terminals to build a production

Variations in CFG Notations → or : : = <> For Non. Terminals Underline the non terminals Symbol for null Λ, ,

Context Free Grammars CFG For identifier ◦ IDENTIFIER → ALPHANUMERIC ◦ ALPHA → A|B|…. |Z|a|b|c…. |z ◦ ALPHANUMERIC → ALPHANUMERIC | Λ ◦ NUMERIC → 0|1|2…|9 ALPHANUMERIC | NUMERIC

Context Free Grammars CFG For arithmetic expressions ◦ ◦ ◦ <expression> + <expression> * <expression> - <expression> + <expression> (<expression>) <expression> <number>

Context Free Grammars Derivation or Generation S → ab. S | Λ S ab. S ◦ ababab ◦ abab

Parse Trees A tree format used for the derivation of a string from the CFG Parse tree, Syntax tree, Derivation tree Generation tree, Production tree, Start symbol of the CFG at root Non terminals are represented as nodes Terminals as leaves Every next level of tree is a derivation from a production of CFG The yield of a parse tree is a terminal string held at all the leaves

Parse Trees Examples ◦ S → ab. S | Λ ◦ Derivation of abab S a b a S b Λ

Derivation Left Most Derivation ◦ If a word w is generated by a CFG by a certain derivation and at each step in the derivation a rule of production is applied to the leftmost nonterminal in the working string then this derivation is called a leftmost derivation Right Most Derivation ◦ If a word w is generated by a CFG by a certain derivation and at each step in the derivation a rule of production is applied to the leftmost nonterminal in the working string then this derivation is called a leftmost derivation

Ambiguity A CFG is called ambiguous if for at least one word in the language that it generated, there are two possible derivations of the word that corresponds to different syntax trees. A CFG which is not ambiguous is called unambiguous CFG

Ambiguous Grammars S → a. S |Sa |a Derivation of aaa S a S S S a a • S → a. S | a a a S S S a a

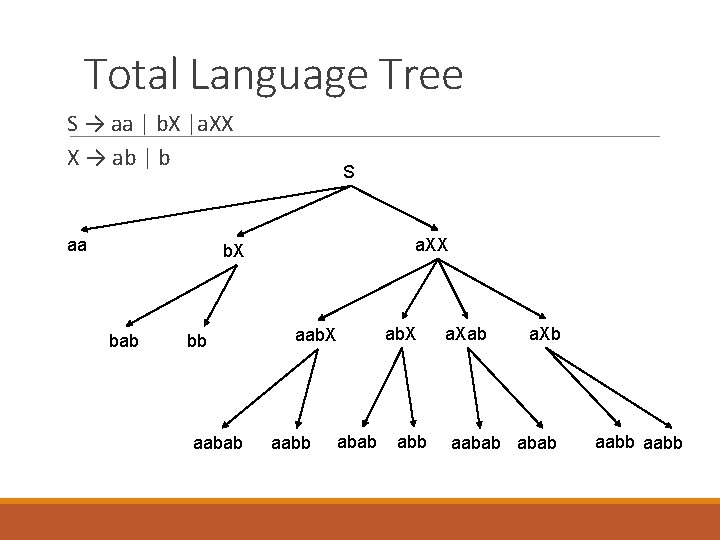
Total language Tree A tree with Start symbol at its root and whose nodes are working strings of terminals and nonterminal The descendant of each node are all the possible results of applying every applicable production to the working string one at a time. A string of all terminals is a terminal node in the tree Total Language Tree

Total Language Tree S → aa | b. X |a. XX X → ab | b aa S a. XX b. X bab bb aabab aab. X aabb abab ab. X abb a. Xab a. Xb aabab aabb

EBNF grammars are not an ideal notation for communicating the rules to the practicing programmer EBNF provides a complex set of recursive rules

EBNF Notational Extensions ◦ An optional element may be indicated by enclosing the element in square brackets [] ◦ A choice of alternatives may use the symbol | within a single rule optionally enclosed by parenthesis if needed ◦ An arbitrary sequence of instances of an element may be indicated by enclosing the element in braces followed by an asterisk {…}*

EBNF Examples ◦ BNF ◦ <integer> : : =<number>| +<number> | -<number> ◦ <number> : : = <digit> | <number><digit> ◦ EBNF ◦ <integer>: : = [+|-]<digit>{<digit>}*

Problems CFG for Variable Declaration ◦ Var. Dec ◦ Type ◦ Identifier ◦ Alpha → Type Identifier; → int | float | double | char → Alphanumeric →a|b|…|z|A|B…|Z ◦ Aplhanumeric → Alphanumeric | Numeric Alphanumeric | Λ ◦ Numeric → 0 | 1 | 2 | … | 9

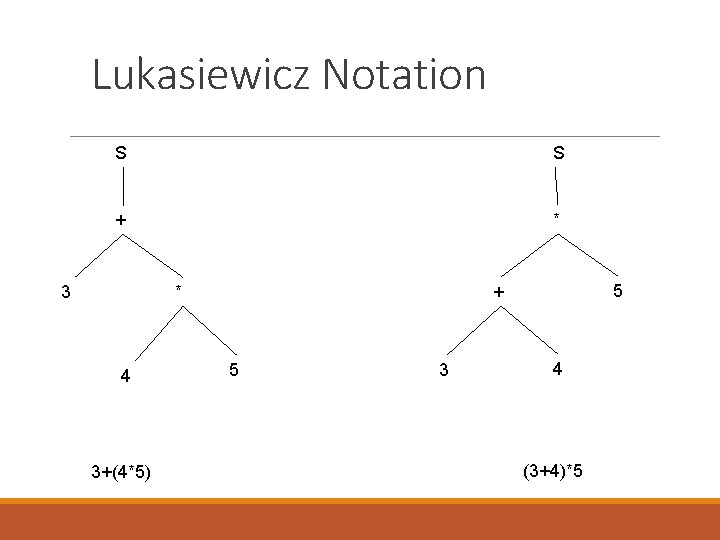
Lukasiewicz Notation Prefix Notation S → S + S| S * S| number ◦ 3+4*5 S → (S + S)|(S * S)| number ◦ Derivations by replacement of NT with calculated results Arithmetic Operators are binary having operands already in proper format

Lukasiewicz Notation S S + * 3 4 3+(4*5) 5 + * 5 3 4 (3+4)*5

Lukasiewicz Notation The operators no more remain nonterminal S → *| + |number + → ++|+*|+number|*+|**|*number| number+| number*| number * → ++|+*|+number|*+|**|*number|number+| number*| number Left most derivation Pre-order traversal of the tree built from this notation gives the expression Evaluation (1+2) * (3+4) * 5 (looking for first o-o-o substring)

Language Span of CFGs All possible languages can be generated by CFGs All regular languages and some of the non-regular languages can be generated by CFGs Some regular (not all) and some non-regular languages can be generated by the CFGs Which statement is true?

Regular Languages and CFG A semiword is a string of terminals(may be none) concatenated with exactly one nonterminal on the right. It is of the form (terminal)…(terminal)Nonterminal

Regular Languages and CFGs All regular languages are also Context Free Therefore CFGs can be written for all RLs Theorem ◦ Given any FA, there is a CFG that generates exactly the same language accepted by the FA. ◦ All regular languages are Context Free ◦ We will prove this using the Constructive Proof of the Theorem i. e. ◦ Reduction of an FA into a CFG describing the same languages

Regular languages and CFGs Conversion Algorithm ◦ The non terminals in the CFG will be all the names of the states in the FA with the start state renamed S. ◦ For every edge at a state X leading to State Y ◦ Create the production X→a. Y and do the same for b edges ◦ For loops add the production X → a. X ◦ For every final state X, create the production X → Λ a x a y x

Regular Languages and CFG The CFG generated through this procedure generates the same language as accepted by the FA Proof ◦ (i) Every word accepted by FA can be generated by CFG ◦ (ii) Every word generated by CFG is accepted by FA

Regular Languages and CFG Example a, b a b S- M a F+ b S → a. M S → b. S M →a. F M →b. S F →a. F F →b. F F→Λ Derivation of babbaaba through CFG and traversal through FA

Regular Languages and CFG FA to CFG ◦ Words that contain a double aa ◦ All words having different first and last letters

Regular Languages and CFG Can a CFG be converted back to an FA, RE or a TG. Need a constructive algorithm if possible Would this algorithm be applicable to all CFGs What about CFGs defining non RLs: Failure !!!! FAs cant be built for non RLs Solution ◦ Differentiate CFGs defining RLs and those defining non RLs

Regular Languages and CFGs Theorem ◦ If all the productions in a given CFG fit one of the two forms ◦ Nonterminal → semiword ◦ Nonterminal → word ◦ Where word can be null, the language generated by this CFG is regular

Regular languages and CFGs Proof ◦ Consider a general CFG of this form ◦ ◦ N 1 → w 1 N 2 → w 2 N 3 → w 3 N 4 →w 5 (Can have many more productions) ◦ Ns are non-terminals while ws are terminals. Together they form a familiar pattern: semiword ◦ Draw and label circles for all Ns and one extra circle labeled with a +. Mark the S circle with -. ◦ For every production of the form Nx → wy. Nz draw a directed edge from state Nx to Nz labelled with the word w ◦ If Nx = Nz then the path is a loop ◦ For every production of the form Np → wq draw a directed edge from Np to + and label it with the word wq, even if wq is Null

Regular Languages and CFGs The resultant figure is a transition graph Each path in this TG from – to + corresponds to a word generated by the CFG Conversely derivation of a word from this CFG corresponds to a path in the TG from – to +. The language of this CFG is regular

Regular Grammars ◦ A CFG is called a regular grammar if each of its productions is of one of the two forms ◦ Nonterminals → semiword ◦ Nonterminals → word Example ◦ S → a. A | b. B ◦ A → a. S | a ◦ B → b. S | b

Λ Productions of the form ◦ N→Λ ◦ are called null (Λ) productions All grammars that generate the Λ string include at least one null production Some grammars that do not generate Λ string still might contain null productions ◦ S → a. X ◦ X→Λ

Λ Productions Hazards of Λ Productions ◦ Create ambiguity in word derivation ◦ Pose problems in some advanced algorithms following shortly Solution ◦ Kill Them !!!

Killing Null Productions Theorem ◦ If L is a context free language generated by CFG that includes Λproductions then there is a different CFG that has no Λproductions that generates exactly the same language L with the exception of only Λ.

Killing Λ Productions Constructive Algorithm ◦ Identify Null Productions ◦ Remove each of them one by one ◦ For each NT having a null production, add productions where the NT has been replaced by null Example ◦ S a. Sa | b. Sb |Λ becomes ◦ S a. Sa | b. Sb |aa |bb

Killing Λ Productions Problem Identified !!! ◦ S a | Xb | a. Ya ◦ X Y|Λ ◦ Y b|X

Killing Λ Productions Null able Non-terminal ◦ In CFG a nonterminal N is called nullable if ◦ There is a production N → Λ, or ◦ There is a derivation that starts at N and leads to Λ (N …. Λ)

Killing Λ Productions Problem Solved !!! Modified Replacement Rule ◦ Delete all Λ-productions ◦ Add the following productions: For every production X → old string add new productions of the form X →. . Where the right side will account for any modification of the old string that can be formed by deleting all possible subsets of nullable nonterminals while avoiding introduction of a null production in this process

Killing Null Productions Not So Fast !!!!! ◦ S → Xay | YY | a. X | ZYX ◦ X → Za | b. Z | ZZ | Yb ◦ Y → Ya| XY | Λ ◦ Z → a. X | YYY ◦ How could one identify a nullable NT in such a complex grammar Solution ◦ A bucket of Blue Paint

Example Consider the CFG S a | Xb | a. Ya X Y|Λ Y b|X Old nullable Production New Production X Y nothing X Λ nothing Y X nothing S Xb S a. Ya So the new CFG is S b S a | Xb | aa | a. Ya |b X Y Y b|X S aa 60

Example Consider the CFG S Xa X a. X | b. X | Λ Old nullable Production S Xa New So the new CFG is roduction S a S a | Xa X a. X | b. X | a | b X a. X X a X b. X X b 61

Example S XY X Zb Y b. W Z AB W Z A a. A | b. A | Λ B Ba | Bb | Λ • Null-able Non-terminals are? • A, B, Z and W 62

S XY X Zb Y b. W Z AB W Z A a. A | b. A | Λ B Ba | Bb | Λ Example Contd. Old nullable New Production X Zb Y b. W Z AB X b Y b Z A and Z B W Z Nothing new A a. A A a A b. A A b B Ba B Bb B b So the new CFG is S XY X Zb | b Y b. W | b Z AB | A | B W Z A a. A | b. A | a | b B Ba | a | b 63

Unit Productions A production of the form ◦ Nonterminal → one Nonterminal ◦ Is called a unit production Unit productions are some times required to change the form of a working string ◦ (Arbitrary)A(arbitrary) ◦ (Arbitrary)B(Arbitrary) Unit Production are also problematic and thus need to be exterminated

Killing Unit Productions Theorem ◦ If there is a CFG for the language that has no Λ-productions, then there is also a CFG for L with no Λ-productions and no unit productions

Killing Unit Productions Naïve Elimination Rule ◦ Eliminate unit productions one by one and replace them with new productions without changing the language being generated by the CFG ◦ Infinite loop and no benefit ◦ Example ◦ S → A |bb ◦ A→B|b ◦ B→S|a Modified Elimination Rule ◦ Eliminate all unit productions simultaneously ◦ Look for any sequence of productions that lead to a replacement with a unit production. Replace all such derived unit productions with the final replacement.

Killing Unit Productions Example ◦ S → A | bb ◦ A→B|b ◦ B→S|a Unit Productions ◦ S→A ◦ A→B ◦ B→S Derived Unit Production ◦ S→A→B ◦ A→B→S ◦ B→S→A

Killing Unit Productions New CFG ◦ S → bb|b|a ◦ A → b|a|bb ◦ B → a|bb|b

New Format for CFG Theorem ◦ If L is a language generated by some CFG, then there is another CFG that generated all the non-Λ words of L, all of whose productions are of one of the two basic forms ◦ Nonterminal → string of only Nonterminals ◦ Nonterminal → one terminal

New Format for CFG Proof ◦ Suppose a CFG contains non terminals S, X 1, X 2, X 3 … and two terminals a and b ◦ Add two new nonterminals A and B and two productions ◦ A→a ◦ B→b ◦ For every previous production involving terminals, replace each a with the nonterminal a and b with the nonterminal B ◦ Any production which is already in the desired form should be left untouched to avoid introduction of unit productions ◦ All the productions now are of the form ◦ Nonterminal → strings of only nonterminals ◦ Nonterminal → one terminal

New format for CFG Example ◦ S → X 1 | X 2 a. X 2 | a. Sb | b ◦ X 1 → X 2 X 2 | b ◦ X 2 → a. X 2 | aa. X 1

Chomsky Normal Form: The Ultimate Target ! If a CFG has only productions of the form ◦ Nonterminals → strings of exactly two Nonterminals ◦ Nonterminals → one terminal It is said to be in Chomsky Normal Form, or CNF Theorem ◦ For any context Free language L, the non Λ words of the language can be generated by a CFG in CNF format

CNF Proof ◦ Any CFG can be converted to the following format ◦ Nonterminal → strings of Nonterminals or ◦ Nonterminal → one terminal ◦ For this new CFG modify the productions so that they become in the CNF ◦ This conversion requires addition of new nonterminals ◦ S → X 1 X 2 X 3 X 4 will be converted to ◦ S → X 1 R 1 ◦ R 1 → X 2 R 2 ◦ R 2 → X 3 X 4

CNF Example ◦ S → a. Sa | b. Sb | a | b | aa | bb CNF ◦ S → AR 1 ◦ R 1 → SA ◦ S → BR 3 ◦ S → AA ◦ S → BB ◦S→b ◦S→a ◦A→a ◦B→b