Contest Algorithms January 2016 5 Divide Conquer Pseudocode

Contest Algorithms January 2016 5. Divide & Conquer Pseudo-code for divide and conquer, and three examples (binary exponentiation, binary search, and mergesort). Contest Algorithms: 5. Divide & Conquer 1

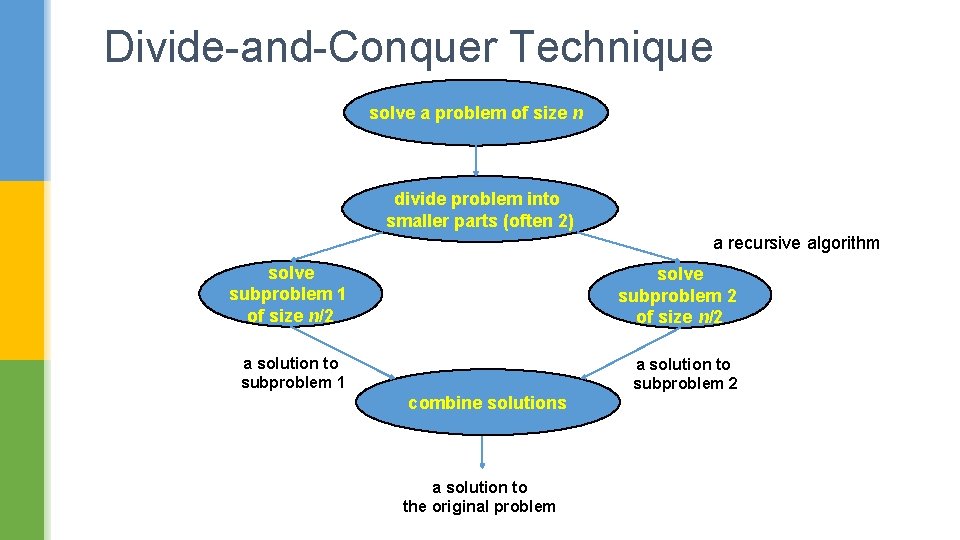
1. Divide-and-Conquer 1. Divide problem into two or more smaller instances 2. Solve smaller instances recursively (conquer) 3. Obtain solution to original (larger) problem by combining these solutions

Divide-and-Conquer Technique solve a problem of size n divide problem into smaller parts (often 2) a recursive algorithm solve subproblem 1 of size n/2 solve subproblem 2 of size n/2 a solution to subproblem 1 a solution to subproblem 2 combine solutions a solution to the original problem

Divide-and-Conquer Examples § Binary exponentiation § Binary search § Sorting: mergesort and quicksort § (see Quick. Sort. java) § Closest Pair of Points Problem § see the Computational Geometry slides

2. Binary Exponentiation : xn see Power. java public static long pow(long x, long n) { if (n <= 0) // n must be positive return 1; else if (n % 2 == 1) { // odd long p = pow(x, (n-1)/2); // pow of x faster than x 2 return x * p; } else { // n even long p = pow(x, n/2); return p * p; } } // end of pow() 5

Writing long numbers § Java interprets all numeral literals as 32 -bit integers. § e. g. long x = 30000000; // will give "integer number too large" error § int range: -2147483648 to 2147483647 (231 -1) § If you want to write something bigger than a 32 -bit integer, use the suffix L: § e. g. long x = 30000000 L; Contest Algorithms: 4. Backtracking // accepted 6

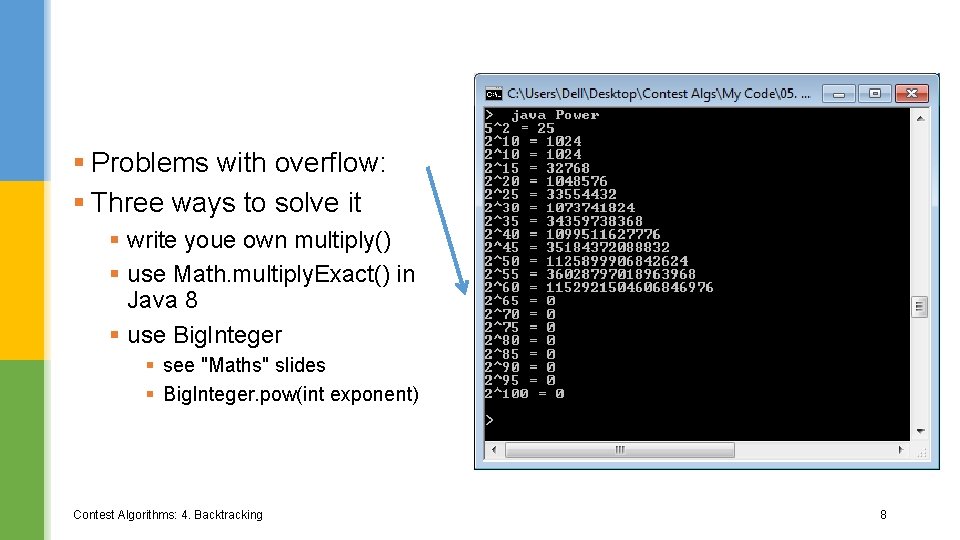
Using pow() public static void main (String[] args) { System. out. println("5^2 = " + pow(5, 2)); System. out. println("2^10 = " + pow(2, 10)); for (int i=10; i <= 100; i=i+5) System. out. println("2^" + i + " = " + pow(2, i)); } // end of main() Contest Algorithms: 4. Backtracking 7

§ Problems with overflow: § Three ways to solve it § write youe own multiply() § use Math. multiply. Exact() in Java 8 § use Big. Integer § see "Maths" slides § Big. Integer. pow(int exponent) Contest Algorithms: 4. Backtracking 8

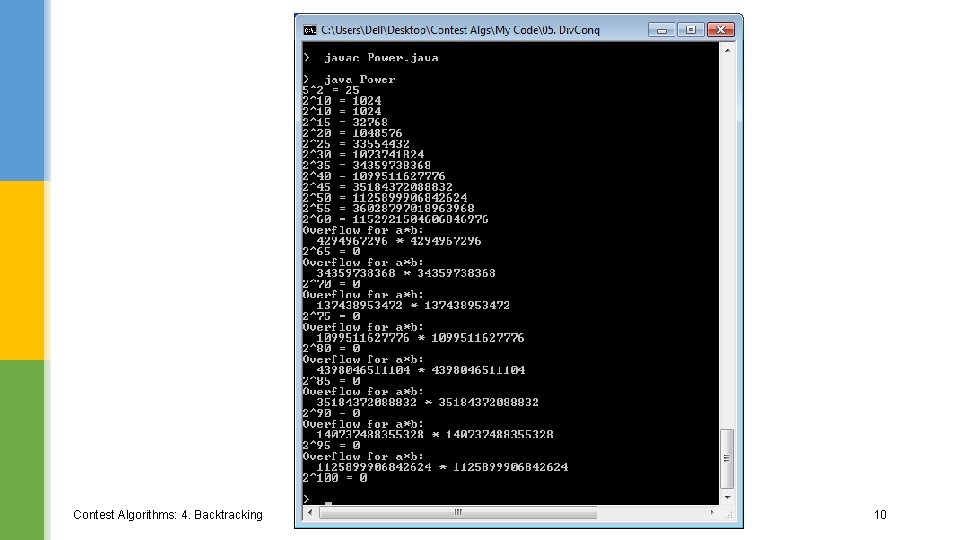
Your own multiply() public static long mult(long a, long b) { if ((a != 0) && (b > Long. MAX_VALUE / a)) System. out. println("Overflow for a*b: n return a*b; } // detect overflow " + a + " * " + b); § In pow(), replace three uses of "*": § return mult(x, mult(p, p)); § return mult(p, p); Contest Algorithms: 4. Backtracking // was x * p // was p * p 9

Contest Algorithms: 4. Backtracking 10

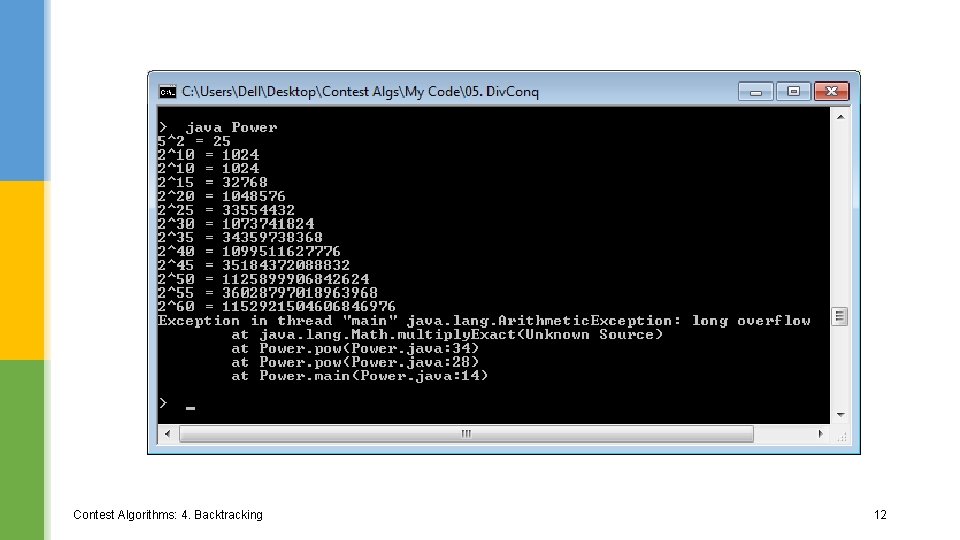
Use Math. multiply. Exact() § In pow(), replace three uses of "*": § return Math. multiply. Exact(x, Math. multiply. Exact(p, p)); // was x * p § return Math. multiply. Exact(p, p); Contest Algorithms: 4. Backtracking // was p * p 11

Contest Algorithms: 4. Backtracking 12

Java 8 "Exact" Math methods § add. Exact(), subtract. Exact(), multiply. Exact() § increment. Exact(), decrement. Exact() § to. Int. Exact() § used when casting a long to an int § Instead of silently giving the wrong answer, they will throw a java. lang. Arithmetic. Exception for overflows involving int or long calculations Contest Algorithms: 4. Backtracking 13

As implemented in Java by Arrays. binary. Search() 3. Binary Search § Binary Search is a divide and conquer algorithm. § Find an element in a sorted array: 1. Divide: Check middle element. 2. Conquer: Recursively search 1 subarray. 3. Combine: Easy; return index Example: Find 9 3 5 7 8 9 12 15

Example Find an element in a sorted array: 1. Divide: Check middle element. 2. Conquer: Recursively search 1 subarray. 3. Combine: Trivial. Example: Find 9 3 5 7 8 9 12 15

Find an element in a sorted array: 1. Divide: Check middle element. 2. Conquer: Recursively search 1 subarray. 3. Combine: Trivial. Example: Find 9 3 5 7 8 9 12 15

Find an element in a sorted array: 1. Divide: Check middle element. 2. Conquer: Recursively search 1 subarray. 3. Combine: Trivial. Example: Find 9 3 5 7 8 9 12 15

Find an element in a sorted array: 1. Divide: Check middle element. 2. Conquer: Recursively search 1 subarray. 3. Combine: Trivial. Example: Find 9 3 5 7 8 9 12 15

Find an element in a sorted array: 1. Divide: Check middle element. 2. Conquer: Recursively search 1 subarray. 3. Combine: Trivial. Example: Find 9 3 5 7 8 9 12 15

Binary Search Code see Binary. Search. Test. java private static int binary. Search(int[] arr, int val) { return bin. Srch(arr, val, 0, arr. length-1); } private static int bin. Srch(int[] arr, int val, int start, int end) { if (start > end) // val not found return -1; int middle = (start + end)/2; int mid. Val = arr[middle]; if (val == mid. Val) return middle; else if (val > mid. Val) // search right half return bin. Srch(arr, val, middle+1, end); else // search left half return bin. Srch(arr, val, start, middle-1); } // end of bin. Srch()

Using Both Functions public static void main (String[] args) { Integer[] int. Arr = {2, 3, 5, 7, 9, 10, 13, 15, 17, 19}; System. out. println("Index pos of 10: " + Index pos of 10: 5 Arrays. binary. Search(int. Arr, 10)); Index pos of 22: -11 System. out. println("Index pos of 22: " + Index pos of 10: 5 Arrays. binary. Search(int. Arr, 22)); Index pos of 22: -1 int[] arr = {2, 3, 5, 7, 9, 10, 13, 15, 17, 19}; System. out. println("Index pos of 10: " + binary. Search(arr, 10)); System. out. println("Index pos of 22: " + binary. Search(arr, 22)); } // end of main() Contest Algorithms: 4. Backtracking 21

4. Mergesort § A stable sorting algorithm with worst-case running time O(n log n) § Algorithm: § Divide the list into two sub-lists § Sort each sub-list (recursion) § Merge the two sorted sub-lists 22

Code see Merge. Sort. java public static void merge. Sort(int[] arr) { int[] temp = new int[arr. length]; msort(arr, temp, 0, arr. length); } private static void msort(int[] arr, int[] temp, int left, int right) { // continue only if the sub-array has more than 1 element if ((left + 1) < right) { int mid = (right + left)/2; msort(arr, temp, left, mid); msort(arr, temp, mid, right); merge(arr, temp, left, mid, right); O(n) } } // end of msort() 23

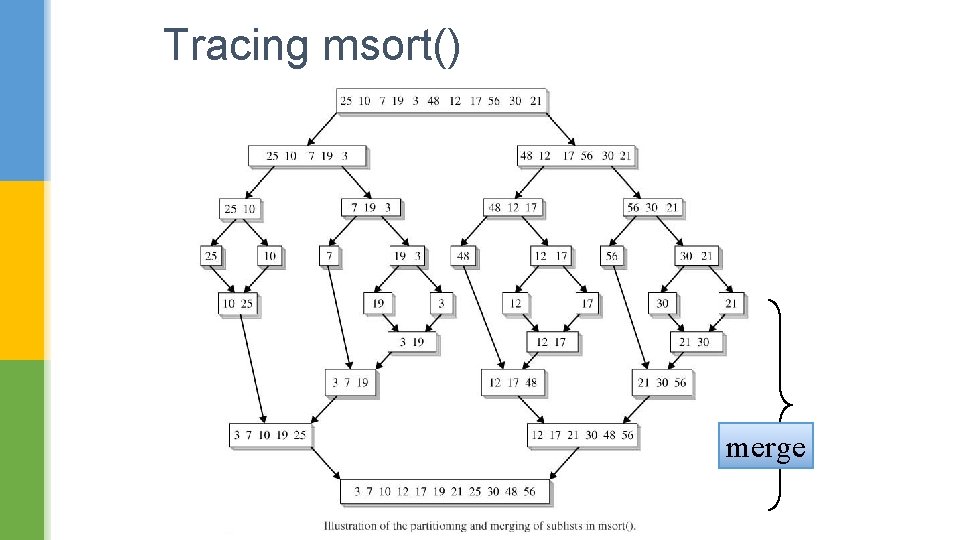
Tracing msort() merge

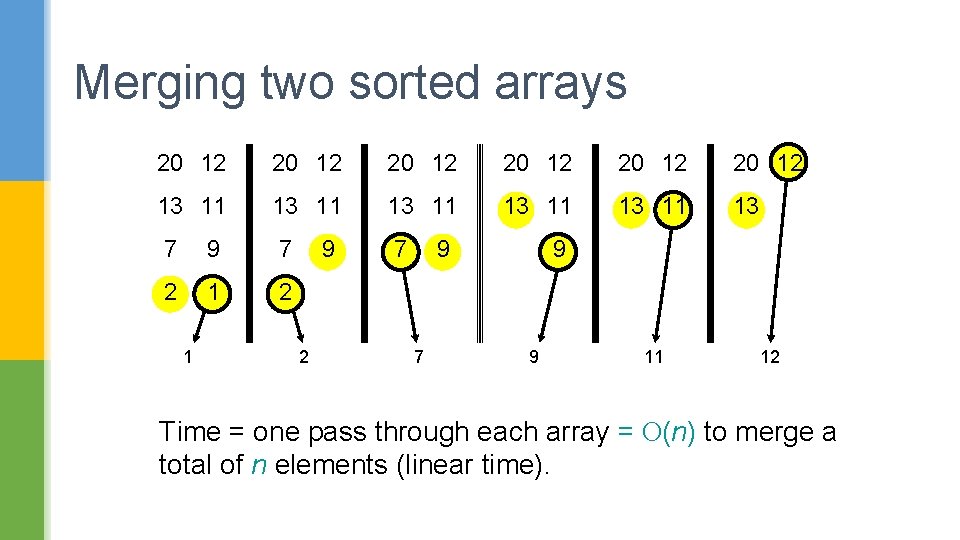
Merging two sorted arrays 20 12 20 12 13 11 13 11 13 7 9 7 2 1 9 2 7 9 9 11 12 Time = one pass through each array = O(n) to merge a total of n elements (linear time).

private static void merge(int[] arr, int[] temp, int left, int mid, int right) { // are the two sub-arrays already in sorted order? if (arr[mid-1] <= arr[mid]) return; int index. A = left; // to scan 1 st sub-array int index. B = mid; // to scan 2 nd sub-array int i = left; // for moving over temp array // compare arr[index. A] and arr[index. B]; copy the smaller to temp while ((index. A < mid) && (index. B < right)) { if (arr[index. A] < arr[index. B]) temp[i++] = arr[index. A++]; // copy and move idxs else temp[i++] = arr[index. B++]; } :

: // copy the tail of the sub-array that is not finished while (index. A < mid) temp[i++] = arr[index. A++]; while (index. B < right) temp[i++] = arr[index. B++]; // copy from temp back to arr for (int j = left; j < right; j++) arr[j] = temp[j]; } // end of merge() Contest Algorithms: 4. Backtracking 39

Using Two Sorts public static void main (String[] args) { int[] arr = {18, 3, 5, 23, 4, 17, 2, 16, 19}; System. out. println("Unsorted array: " + Arrays. to. String(arr)); merge. Sort(arr); System. out. println("Sorted array: " + Arrays. to. String(arr)); Integer[] int. Arr = {18, 3, 5, 23, 4, 17, 2, 16, 19}; Arrays. sort(int. Arr); // quicksort System. out. println("Sorted array: " + Arrays. to. String(int. Arr)); } // end of main() Contest Algorithms: 4. Backtracking 40

Contest Algorithms: 4. Backtracking 41