contenuto Md T parte seconda ancora alcune macchine

contenuto: Md. T - parte seconda ancora alcune macchine di Turing per risolvere semplici problemi : 8) controllo parentesi ben formate (slide 14) 9) sposta un dato su nastro (slide 27) 10) confronto di due valori interi e test <, =, > (slide 39) 11) dato un numero n calcola il valore 2*n (slide 48) 12) cerca stringa di simboli s 2 uguale a una stringa data s 1 (slide 57) 13) una "memoria ad accesso diretto" (slide 65) xx) la macchina di Turing programmabile o 1

8. esempio: controllo parentesi ben formate per l’ esempio seguente (macchina di Turing numero otto) ci servono alcune definizioni preliminari le prossime dieci pagine sono dedicate a questo. . . 2

premessa - definizione di un insieme: 3 un insieme di elementi si puo’ definire in modi diversi, * elencando tutti gli elementi dell’insieme (se e’ finito. . . ) es. insieme { 0, 1 } * fornendo una proprieta’ per gli elementi dell’ insieme, es. insieme degli "studenti di ingegneria iscritti al 1. o anno all’univ. di TS", * specificando delle regole per produrre gli elementi, ovvero per costruire (a partire da un elemento dato -uno o piu’) sistema "generativo"

premessa. . . sulle stringhe di caratteri. . . 4 (*) dato un insieme di caratteri C = {a, b, c, d } definiamo una stringa s come una sequenza di caratteri: es. s 1 = d = stringa di un carattere, s 2 = abba e’ una stringa di 4 caratteri, s 3 = abbccdccbba e’ una stringa di 11 caratteri, definiz: |s| = lunghezza della stringa s = n. di caratteri di s definiz: C * e’ l’insieme di tutte le stringhe che si possono formare con i caratteri di C ( C * <-- leggi " c stellato " ) C * = { s | s = stringa di caratteri appartenenti a C } anche la stringa vuota s 0 appartiene a a C * : s 0, con |s 0| = 0, appartiene a C * __________________

un primo esempio di un insieme di stringhe: sia l’insieme di caratteri di partenza formato dall’unico carattere + allora P = { + } allora l’insieme P stellato P * = { s | s stringa di caratteri di P } e’ l’insieme delle stringhe che si possono formare con + es. : p 0 = (stringa vuota, |p 0| = 0 ) p 1 = + (stringa di un carattere, |p 1| = 1) p 4 = + + (stringa di 4 caratteri, |p 4| = 5

un secondo esempio di un insieme di stringhe A = insieme di due caratteri, parentesi aperta e chiusa: A= { ( ) } allora l’insieme A stellato. . . A * = { s | s stringa di caratteri di A } e’ l’ insieme di tutte le stringhe che si possono formare con le due parentesi, ad es. : s 0 = (stringa vuota) sx = ( (stringa di un carattere solo) sn = ) ) (stringa di 4 caratteri) s 7 = ( ( ) ( ) ) (stringa di 8 caratteri) eccetera. . . A * e’ un insieme infinito: il numero di stringhe che si possono formare con uno o piu’ simboli e’ infinito! 6

continua sugli insiemi di stringhe 7 consideriamo ad es. : B = { 0 1 } allora l’insieme B stellato B * = { s | s stringa di caratteri di B } e' l' insieme di tutte le stringhe che si possono formare con i simboli 0 ed 1: 0, 1, 00, 01, 10, 11, 000, 001, 010, 100, 011, 101, 110, 111, ecc posso definire un X sottoinsieme di B* (di stringhe di 0 ed 1) aggiungendo una proprieta’ richiesta ad una stringa per essere considerata un elemento di X ovvero “ben formata”: es. : X = stringhe s di B *, tali che il numero degli 1 in s e’ pari. quindi 0, 11, 011, 110, 0011, . . , 1111, . . . sono elementi di

ripetizione. . . dei concetti presentati finora 8 insieme C (finito) di caratteri es { x, y, z }. . . una stringa di caratteri su C es s = xxx. . . |s| = lunghezza della stringa s es |xxx| = 3. . . C stellato C* = { s con |s| >= 0, e s=stringa di caratt. di C} da C* definisco altri insiemi X, con X sottoinsieme di C*, introducendo una proprieta’p che chiedo alle stringhe di X: l’insieme X e’ caratterizzato dalla proprieta’ p: definiamo "ben formate" le stringhe di X, cioe’ che sono p, le stringhe di C* che non sono p non appartengono a X non sono ben formate. Nell’es. precedente, B={01} *

cont. stringhe e insiemi e stringhe ben formate. . . 9 es. : B={01} B *= { s | s qualunque stringa di caratteri di B } Y = { s | s appart. a B * e tale che |s| = 3 } ovvero: Y = { 111, 110, 101, 011, 100, 010, 001, 000 } es. : D={1} D *= { s | s stringa di caratteri di D } D * = { 1, 111, 11111, 1111111, . . . } W = { s | dove s appartiene a D *, e dove |s| = 4 } allora: W = { 1111 }

avevamo detto che. . . 10 un insieme di elementi si puo’ definire in modi diversi, * elencando tutti gli elementi dell’insieme (se e’ finito. . . ) es. insieme { 0, 1 } * fornendo una proprieta’ per gli elementi dell’insieme, es. insieme degli studenti di ingegneria iscritti al 1. o anno all’univ. di TS, . . . abbiamo visto alcuni esempi. . . ma si puo’ definire un insieme anche in modo “costruttivo” o “generativo”, * specificando delle regole per produrre gli elementi, ovvero per costruire (a partire da elementi dati) dei nuovi elementi dell’insieme. . . sistema generativo. . .

schema generativo (cont. premesse per la m. d. T nr. 8) defin. di un insieme di stringhe di parentesi “ben formate”: base: ( ) sta in PBF /*/ [pbf = parentesi ben formate ] 1. a regola: se E sta in PBF allora (E) sta in PBF (es. se ( ) e’ PBF, allora ( ( ) ) e’ PBF) 2. a regola: se E ed F stanno in PBF allora EF sta in PBF (es. se ( ) e ( ( ) ) sono PBF, allora ( ) ( ( ) ) e’ PBF) 11

cont. schema generativo (sistema formale generativo) base: ( ) sta in PBF [ pbf = parentesi ben formate ] 1. a regola: se E sta in PBF allora (E) sta in PBF 2. a regola: se E ed F stanno in PBF allora EF sta in PBF limitazione: null’altro sta in PBF. da questo schema generativo possiamo ricavare [fabbricare] tutte le PBF che vogliamo, partendo dalla stringa di base: ( ) ->1 ( ( ) ) ->1 ( ( ( ) ) ) ->1 ( ( ) ) ecc ( a ->1 b significa: applico la regola 1 alla stringa a, e ricavo la stringa b) oppure: ( ) ->2 ( ) ->1 ( ( ) ) ->1 ( ( ( ) ) ) ecc oppure: 12

parentesi ben formate. . . problema: 13 data una stringa di parentesi p , decidere se e’ ben formata oppure no, ovvero decidere se appartiene all'insieme PBF ad es. : ( ), ( ) ( ), ( ( ( ) ) ), ecc sono p. b. f. ( (, ( ( ) ) ( (, ) (, ecc non sono p. b. f. un metodo per decidere potrebbe essere: 1) calcola la lunghezza della stringa data p, |p|, 2) fabbrica un insieme L di tutte le stringhe ben formate di lunghezza minore o uguale a |p| (a partire dalla base, con le regole di derivazione viste), 3) vedi se la stringa data p sta in questo insieme L: 4) se p appartiene a L, allora p e’ ben formata, altrimenti no. questo metodo funziona perche' vi sono solo regole che allungano

parentesi ben formate - problema di decisione 14 MA - lo stesso problema puo’ essere risolto in modo piu’ breve, osservando una proprieta’ fondamentale che hanno tutte le p. b. f. : ogni parentesi chiusa e’preceduta da una parentesi aperta e ogni parentesi aperta e' seguita da una chiusa: ( ), ( ) ( ), ( ( ( ) ) ), ( ( ) ) ecc sono p. b. f. , ( ( ) ) ( (, ) (, ( ) ( ) ) ecc non sono p. b. f. es. : 1) cerco la prima ) nella stringa data (() ()) 2) sostituisco la prima parentesi ) con un 1: ( ( 1 ( ) ) 3) cerco la prima ( che precede la ) appena cancellata: 4) sostituisco questa ( con un uno: (11 ())

parentesi ben formate - problema di decisione 15 questo procedimento [elimina le coppie di parentesi ben formate, la prima “)” e la “(“ corrispondente davanti ] dara’ 0) 1) 1) 1) (() ()) ((1 ()) (11 (1) (11 111 1 1 1 -->> la p e’ una p. b. f. questo procedimento si puo’ formulare in forma di m. d. T. alla fine scriveremo il risultato su nastro in forma di S (si’) oppure N (no). se alla fine rimangono delle parentesi aperte oppure non

due esempi con stringhe non ben formate: 16 1) cerco la prima ) nella stringa data ( ) ) ) 2) sostituisco la prima parentesi ) con un 1: ( 1 ) ) 3) cerco la prima “(“ che precede la “)” appena cancellata: 4) sostituisco questa ( con un uno: 1 1 ) ) 5) ripeto da istruzione 1, e ottengo 1 1 1 ) 6) ora torno indietro per cancellare una “(“ -ma non la trovo, 7) allora fine: la stringa non e’ ben formata - troppe “)” 1) cerco la prima ) nella stringa data ( ( ( ) 2) sostituisco la prima parentesi ) con un 1: ( ( ( 1 3) cerco la prima “(“ che precede la “)” appena cancellata: 4) sostituisco questa ( con un uno: ( ( 1 1

8. ) m. d. T. : controllo parentesi ben formate. . A ( ( ) ) A. . a a ( + ; ricerca della prima ), scorri le ( a ) b 1 - ; trovata ), cancella, cerca ( corrisp. b ( a 1 + ; trovata (. . . a 1 + ; se trovi 1 ignora: b 1 - ; se trovi 1 ignora: avremo la successione: 1) A ( ( ) ) A. 5) A ( 1 1 ( ) ) A. . a a 2) A ( ( ) ) A. 6) A ( 1 1 ( ) ) A. . a a 3) A ( ( ) ) A. 7) A ( 1 1 ( ) ) A. . a a 4) A ( ( 1 ( ) ) A. 8) A ( 1 1 ( 1 ) A. . b b 17

8. ) m. d. T. : controllo par. ben form. [elimina coppie ( ) ] . . A ( ( ) ) A. . a a ( + ; ricerca della prima ) b 1 - ; trovata, cancella, cerca ( corrisp. b ( a 1 + ; se in b trovi ( e'il paio cercato! a 1 + ; scorri a destra se in a, b 1 - ; a sin. se in b. . . avremo: 1) A ( ( ) ) A. 10) A ( 1 1 ) A. . a a 7) A ( 1 1 ( ) ) A. . 11) A ( 1 1 1 A. . a b 8) A ( 1 1 ( 1 ) A. . 14) A ( 1 1 1 A. . b b 9) A ( 1 1 ) A. . 15) A ( 1 1 1 A. . a b 18

8. ) m. d. T. : controllo par. ben form. [elimina coppie ( ) 19 ] a ( + ; ricerca della prima ) b 1 - ; trovata, cancella, cerca ( corrisp. b ( a 1 + ; ripeti. . . se trovi 1 ignora: a 1 a 1+ ; b 1 - ; . . . avremo la successione: b A h N 0 ; se non trovi ( allora non ok! a. Ac. A- ; 1) A ( ( ) ) A. . . 17) A 1 1 1 A. . a a 15) A ( 1 1 1 A. . . b 16) A 1 1 1 A. . 20) A 1 1 1 A. . a a ho finito le ), arrivo fino al delimitatore A -> devo prevedere anche questo caso. . . mi rimane da controllare se e’rimasta qualche

8. ) m. d. T. : controllo par. ben form. [controllo finale] a ( + ; ricerca della prima ) b 1 - ; trovata, cancella, cerca ( corrisp. a 1 + ; ignoro gli 1 in mezzo. . . a A c A - ; stato a, va a destra, nessuna ) trovata ; da controllare se e’rimasta una ( c 1 - ; scorri verso sinistra. . . c A h S 0 ; se non hai trovato nessuna ( -> ok 1) A ( ( ) ) A. 22) A 1 1 1 A. . a c 15) A 1 1 1 A. . 26) A 1 1 1 A. . a c 20) A 1 1 1 A. . 27) A 1 1 1 A. . a c 21) A 1 1 1 A. . 28) S 1 1 1 A. . c h ho esaminato il dato, la risposta e’ si’. 20

8) m. d. T. controllo par. ben form. situazioni stringa NON ok quintuple: c 1 - ; scorri verso sinistra. . . c A h S 0 ; se non hai trovato nessuna ( -> ok c ( h N 0 ; caso di stringa errata esempio di stringa non ben formata: . . A ( ( ) A situazione non ok: a applico le regole, arrivo a: . . A ( 1 1 ( ) A. . cancello la prima ) e la a. . sua ( corrispondente. . A ( 1 1 A. . via la seconda ) e la sua ( a. . corrispondente. . A ( 1 1 A. . cerca ancora qualche ) a. . non c’e’- vai in stato c. . A ( 1 1 A. . a controllare se c’e’ una ( c. . c’e’ una ( e non c'e'piu' ). . A ( 1 1 A. . se in c trovo una ( allora c. . la stringa non e’ok: 21

8) m. d. T. par. ben formate - 2 caso di stringa NON ok altro esempio di stringa non ben formata: . . A ( ) ) A situazione non ok: a applico le regole, arrivo a: . . A 1 1 ( ) ) A. . cancello la prima ) e la ( a. . trovo una ) e cancello. . A 1 1 ) A. . cont. a cercare una ). . a. . trovo una ) e la cancello, . . A 1 1 1 A. . cerco la sua ( corrispond. b. . che pero’ non trovero’: . . A 1 1 1 A. . finora avevo: b ( a 1 + b. . e la b 1 b 1. . N 1 1 1 A. . se in stato b trovo A->err h. . agg. quintupla b A h N 0 22

8) m. d. T. par. ben formate rivediamo le quintuple finora definite ; stato a cerca una ) e cancella a ( + ; ricerca di una ) - ignora ( a ) b 1 - ; trovata, cancella, cerca ( corrisp. a 1 + ; ricerca di una ) - ignora 1 a A c A - ; non ho trovato una ), rimane da ; controllare se e’rimasta una ( ; stato b cerca ( corrispond. ad una ) gia’cancellata b ( a 1 + ; se trovi ( cancella e ripeti b 1 - ; se trovi 1 ignora: b A h N 0 ; se non trovi ( allora non ok! b ) ? ; un caso che NON si puo’presentare ; stato c controlla se c’e’ una ( singola. . c ( h N 0 ; c’e’ una ( orfana-> stringa errata! c 1 - ; scorri verso sinistra. . . c A h S 0 ; non ho trovato nessuna ( allora ok c ) ? ; un caso che NON si puo’presentare 23

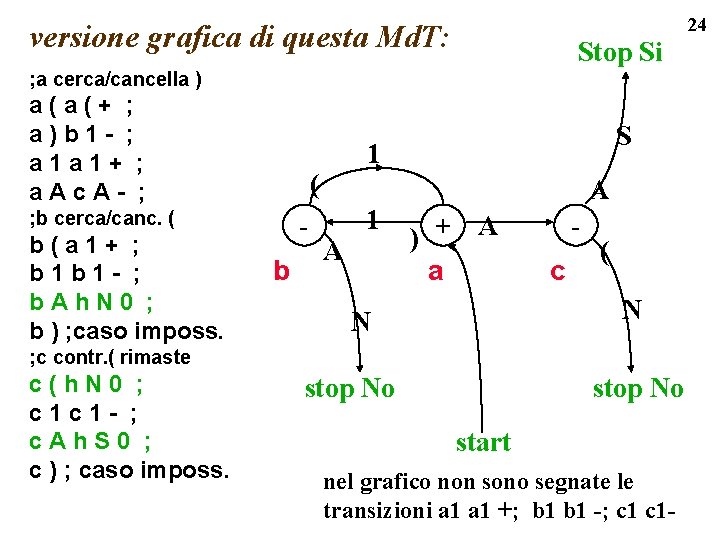
24 versione grafica di questa Md. T: Stop Si ; a cerca/cancella ) a(a(+ ; a)b 1 - ; a 1 a 1+ ; a. Ac. A- ; b(a 1+ ; b 1 b 1 - ; b. Ah. N 0 ; b ) ; caso imposs. 1 ( ; b cerca/canc. ( b S A 1 A ) + A a c ( N N ; c contr. ( rimaste c(h. N 0 ; c 1 c 1 - ; c. Ah. S 0 ; c ) ; caso imposs. stop No start nel grafico non sono segnate le transizioni a 1 +; b 1 -; c 1 -

8. o esempio di m. d. T. osservazione finale: L’esempio visto pero’ distrugge i dati: esercizio: modificare l’algoritmo in modo che la macchina NON distrugga i dati (provare da soli. . . ) (suggerimento: nella verifica delle coppie “)” e “(“ invece di sostituire entrambe le parentesi con un simbolo, si cambi la “)” in un simbolo x e la “(“ in un simbolo diverso y, e alla fine sara' facile ripristinare la situazione iniziale. 25

Macchine di Turing 26 Abbiamo visto che una Md. T puo' realizzare alcune procedure di calcolo semplici, riempi il nastro di uni, come incrementa un numero n di uno, controlla se il numero di uni in una stringa di zeri e uni e' pari controlla se una stringa di ( e di ) e' ben formata; vediamo ancora qualche esempio di Md. T che realizzano alcune operazioni tipiche di tutti i calcolatori: sposta un dato, test se un due numeri sono uguali, ecc

Md. T numero 9 : sposta (muovi) uni 27 due esempi di operazioni di base: Md. T numero 9 : sposta (muovi) uni dato un nastro: . . 0 0 0 * 1 1 1 0 0 0. . a spostare gli uni dall’altra parte cioe’ produrre. . 0 0 1 1 1 * 0 0 0. . h devo trovare una procedura per ottenere il risultato voluto. .

Md. T numero 9 : sposta (muovi) uni 28 dato un nastro: . . 0 0 0 * 1 1 1 0 0 0. . a produrre . . 0 0 1 1 1 * 0 0 0. . h una procedura puo’ essere: cerco il primo 1 che trovo a destra dell’ asterisco, lo cancello e scrivo un 1 a sinistra dopo l’ asterisco: . . 0 0 1 * 0 1 1 0 0 0 poi cerco il prossimo a uno a destra dell' *. . 0 0 0 1 1 * 0 0 1 0 0 0 lo cancello e lo a scrivo a sinistra. . .

Md. T numero 9 : sposta (muovi) uni una strategia: cancello il primo 1 a destra dell’ * e riscrivo 1 a sinistra. . 0 0 0 * 1 1 1 0 0 0. . stato a cerca 1 a destra dell'* a cancello il primo uno che trovo. . 0 0 0 * 0 1 1 0 0 0. . sono in stato c, vai a sinistra c e cerca l' *. . 0 0 0 * 0 1 1 0 0 0. . scavalco *, passo in stato d d cerco 0 a sinistra dell'*. . 0 0 1 * 0 1 1 0 0 0. . in stato d cambio 0 in 1, poi e in stato e a destra fino all' *, . . 0 0 1 * 0 1 1 0 0 0. . ripeto: cerca 1, cancella e a porta 1 a sinistra: . . 0 0 0 1 1 * 0 0 1 0 0 0. . in stato d il 1. o zero a sinist e cambia in 1, in stato e a destra. . 0 0 1 1 1 * 0 0 0. . ho portato tutti gli 1, ripeto a vado a cercare ancora 1. . . ma: . . 0 0 0 * 0 0 0. . non c'e'piu'nessun 1, lo stato a a va a destra su nastro vuoto e NON SI FERMA PIU' !!! --> 29

Md. T numero 9 : sposta (muovi) uni una strategia: cancello il primo 1 a destra dell’ * e riscrivo 1 a sinistra. . 0 0 0 * 1 1 1 0 0 0. . stato a cerca 1 a destra dell'* a sostituisco il primo 1 con una x. . 0 0 0 * x 1 1 0 0 0. . stato c vai a sinistra c e cerca l' *. . 0 0 0 * x 1 1 0 0 0. . scavalco 0, sempre in stato c c cerco 0 a sinistra dell'* e. . 0 0 1 * x 1 1 0 0 0. . in stato c cambio 0 in 1, poi e in stato e scorri 1 a sin di *. . 0 0 1 * x 1 1 0 0 0. . ripeto: in a, cerca 1, cancella, a e porta 1 a sinistra: . . 0 0 0 1 1 * x x 1 0 0 0. . in stato c il 1. o zero a sinist e cambia in 1, in stato e, a dest. . . 0 0 1 1 1 * x x x 0 0 0. . ho portato tutti gli 1, ripeto a vado a cercare ancora 1. . . ma: . . 0 0 0 * x x x 0 0 0. . non c'e'piu'nessun 1, lo stato a a va a destra fino a zero, e allora. . 0 0 0 * x x x 0 0 0. . SI FERMA; ora si cancellera' f in f le x a destra dell' * 30

Md. T numero 9 : sposta (muovi) uni meglio: cercare l’ultimo 1 a destra: a*b*+ b 1 b 1+ b 0 c 0 c 1 d 0 - ; scorri a destra e vai in b; stato b indica che ; sono a destra del *; in stato b ignora 1 cerca 0 ; vai oltre gli uni, allo zero torna a sinistra ; in stato c cancella 1; stato d=cancellato 1 dato il nastro qui sotto applico le quintuple scritte sopra: . . 0 0 0 * 1 1 1 0 0 0. . 1) passo, iniziale a. . 0 0 0 * 1 1 1 0 0 0. . 2) in stato b scorri a destra b e cerca lo zero = fine degli uni. . 0 0 0 * 1 1 1 0 0 0. . 4) scorrimento a destra b. . 0 0 0 * 1 1 1 0 0 0. . 5) zero limite degli 1 a destra b. . 0 0 0 * 1 1 1 0 0 0. . 6) torno a sinistra su ultimo 1 c. . 0 0 0 * 1 1 0 0. . 7) cancello 1, e vado a sinistra d a riscrivere 1 dopo l' * 31

Md. T numero 9 : sposta (muovi) uni a * b * + ; scorri a destra - b indica che b 1 + ; sono a destra del *; ignora 1 b 0 c 0 - ; oltre gli uni - torna a sinistra c 1 d 0 - ; cancella 1; stato d=cancellato 1 d * - ; d aggiunge 1 a sinistra. . . d 1 - ; ignorando 1 d 0 a 1 + ; scrivo 1 (ho spostato un 1) e ripeto. . 0 0 0 * 1 1 0 0. . 8) vado a sinistra scorrendo d gli uni a destra dell' *. . 0 0 0 * 1 1 0 0. . 9) sono in mezzo, ancora a sin d. . 0 0 0 * 1 1 0 0. . 10) cerca 0 a sinistra di * d trovato 0 a sinistra di *. . 0 0 1 * 1 1 0 0. . 11) e scrivo un 1, e ripeto a 32

Md. T numero 9 : sposta (muovi) uni a * b * + ; scorri a destra; stato b indica b 1 + ; che sono a destra del *; ignora 1 b 0 c 0 - ; oltre gli uni - torna a sinistra c 1 d 0 - ; cancella 1; stato d=cancellato 1 d * - ; d aggiunge 1 a sinistra. . . d 1 - ; ignorando 1 d 0 a 1 + ; scrivo 1, passo in stato a, e ripeto. . 0 0 1 * 1 1 0 0. . 12) passa l' * a. . 0 0 1 * 1 1 0 0. . 13) in b cerca ultimo 1. . b. . 0 0 1 * 1 1 0 0. . 15) in b fine dato a dest b. . 0 0 1 * 1 1 0 0. . 16) ritorna a sinistra, cancella c. . 0 0 1 * 1 0 0 0. . 17) e scrivi 1 a sinistra d 33

Md. T numero 9 : sposta (muovi) uni a * b * + ; scorri a destra stato b indica che b 1 + ; sono a destra del *; ignora 1 b 0 c 0 - ; oltre gli uni - torna a sinistra c 1 d 0 - ; cancella 1; stato d=cancellato 1 d * - ; d aggiunge 1 a sinistra. . . d 1 - ; ignorando 1 d 0 a 1 + ; scrivo 1 e ripeto a 1 + ; se in stato a trovo 1 ignoro. . . 0 0 1 * 1 0 0 0. . vai a sinistra d. . 0 0 1 * 1 0 0 0. . riscrivi d. . 0 0 0 1 1 * 1 0 0 0. . e ripeti a. . 0 0 0 1 1 * 1 0 0 0. . di nuovo. . b 34

Md. T numero 9 : sposta (muovi) uni a * b * + ; scorri a destra - b indica che b 1 + ; sono a destra del *; ignora 1 b 0 c 0 - ; oltre gli uni - torna a sinistra c 1 d 0 - ; cancella 1; stato d=cancellato 1 d * - ; d aggiunge 1 a sinistra. . . d 1 - ; ignorando 1 d 0 a 1 + ; scrivo 1 e ripeto. . . a 1 + ; se in stato a trovo 1 ignoro. . . 0 0 0 1 1 * 1 0 0 0. . limite dato b. . 0 0 0 1 1 * 1 0 0 0. . cancella 1 e poi c. . 0 0 0 1 1 * 0 0 0. . riscrivi 1 a sin. d. . 0 0 1 1 1 * 0 0 0. . ripeti: a ripeto, cerco 1 a destra dell'asterisco - ma ora non c'e' piu' 35

Md. T numero 9 : sposta (muovi) uni a * b * + ; scorri a destra - b indica che b 1 + ; sono a destra del *; ignora 1 b 0 c 0 - ; oltre gli uni - torna a sinistra c 1 d 0 - ; cancella 1; stato d=cancellato 1 c * h * 0 ; non c’e’ nessun 1 a destra->stop d * - ; d aggiunge 1 a sinistra. . . d 1 - ; ignorando 1 d 0 a 1 + ; scrivo 1 e ripeto. . . a 1 + ; se in stato a trovo 1 ignoro. . . 0 0 1 1 1 * 0 0 0. . ripeti: cerca 1 a des a. . 0 0 1 1 1 * 0 0 0. . sono sul limite dato, torno b a sinistra in c, ma non c'e' 1. . 0 0 1 1 1 * 0 0 0. . trovo un *, non vi sono 1 da c cancellare, quindi mi fermo: . . 0 0 1 1 1 * 0 0 0. . stop h 36

Md. T numero 9 : sposta (muovi) uni esempio muovi gli uni. . . provare a scrivere la versione grafica come esercizio dato un nastro: . . 0 0 0 * 1 1 1 0 0 0. . a date le quintuple: a * b * + ; scorri a destra - b indica che b 1 + ; sono a destra del *; ignora 1 b 0 c 0 - ; oltre gli uni - torna a sinistra c 1 d 0 - ; cancella 1; stato d=cancellato 1 c * h * 0 ; non c’e’ nessun 1 a destra->stop d * - ; d aggiunge 1 a sinistra. . . d 1 - ; ignorando 1 d 0 a 1 + ; scrivo 1 e ripeto. . . a 1 + ; se in stato a trovo 1 ignoro. . . 37

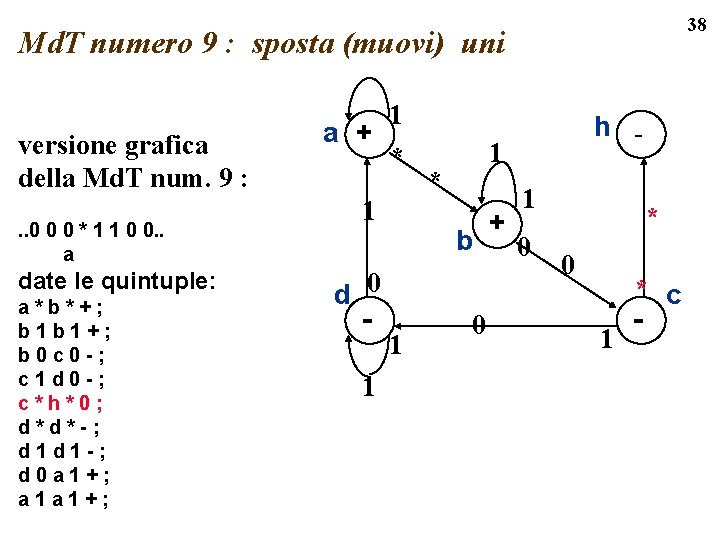
38 Md. T numero 9 : sposta (muovi) uni versione grafica della Md. T num. 9 : . . 0 0 0 * 1 1 0 0. . a date le quintuple: a*b*+; b 1 b 1+; b 0 c 0 -; c 1 d 0 -; c*h*0; d*d*-; d 1 d 1 -; d 0 a 1+; a 1 a 1+; 1 a + * 1 d 0 1 1 * b 1 h - 0 + 1 0 * 0 1 * c -

10) Md. T: test se due dati hanno valore uguale 10) esempio: una macchina di Turing per il confronto di due valori numerici, ovvero test se a<b oppure se a=b oppure se a>b 39

10) Md. T: test se due dati hanno valore uguale 2. o esempio di operazioni di base: 40 test se a=b ipotesi sulla rappresentazione di dati: in unario, separati da un *, posizione iniziale testina in mezzo: . . . 0 0 1 * 1 1 0 0. . a schema di soluzione (algoritmo in notazione informale) : fintanto che a>0 e b>0 { sottrai 1 ad entrambi cioe’ fai b-1 e poi fai a-1 } ora, se a=0 oppure b=0 { controlla se entrambi sono zero, se si’ il test risponde S, se no risponde N }

10) Md. T : test se a=b es. con a=1, b= 2: dato a dato b ; sottrai 1 a b: . . 0 0 1 * 1 1 0 0. . a * b * + ; vai a destra a b 1 + ; scorri il dato b cerca ultimo 1 b 0 c 0 - ; sono oltre il limite di b, torna a sin c 1 d 0 - ; cancella un 1 di b (come nella muovi 1) ; ora abbiamo: . . 0 0 1 * 1 0 0 0. . ; ora sottrai 1 ad a: d d 1 - ; scorri a sinistra per fare a-1 d * - ; scavalca *, vai a vedere dato a d 0 e 0 + ; sei oltre a, ritorna a destra e 1 a 0 + ; fatto b-1 e anche a-1 : ripeti a 1 + ; scorri il dato a. . . fino all’ * ; ora abbiamo: . . 0 0 0 * 1 0 0 0. . ; a 41

10) Md. T: test se a=b vediamo avanti. . . caso a<b : ; sottrai 1 a b: . . 0 0 1 * 1 1 0 0. . a * b * + ; vai a destra a b 1 + ; scorri il dato b cerca ultimo 1 b 0 c 0 - ; sono oltre il limite di b, torna a sin c 1 d 0 - ; cancella un 1 di b (come muovi 1) ; ora sottrai 1 ad a: d 1 - ; scorri a sinistra d * - ; scavalca *, vai a vedere dato a d 0 e 0 + ; sei oltre a, ritorna a destra e 1 a 0 + ; fatto b-1 e anche a-1 : ripeti a 1 + ; scorri il dato a. . . fino all’ * ; ora abbiamo: . . 0 0 0 * 1 0 0 0. . ; a ; il ciclo si ripete finche o a oppure b vanno a zero: ; se dopo aver fatto b-1 non trovo alcun 1 in a, ovvero ; se dopo d 0 e 0+ (torna a destra dopo trovato 0 a sin di a) ; cioe' se dopo aver fatto b-1 trovo che a=0 ? ; allora e' b>0, a=0 quindi aggiungo quintupla che e * h < 0 ; "scrive" il risultato, ovvero "minore" a<b 42

10) Md. T : test se a=b se lo stato iniziale e' come a destra (a>b) allora si procede a cancellare un uno a destra (dal dato b, eseguo b -1) e anche a sinistra (dato a, eseguo a-1), come riportato nella traccia di esecuzione qui a destra: traccia gia' seguita prima, ripeto: in stato b cerco fine dato b, quindi uno zero, con (b 0) siamo sul limite destro, torno a sinistra di una posizione in stato c e cancello l'uno piu' a destra di b poi in stato d cerco lo zero limite di a a sinistra, torno indietro in stato e e cancello l'uno piu' a sinistra di a, e ritorno nello stato a; 43. . 0 1 1 * 1 0 0. . a. . 0 1 1 * 1 0 0. . b. . 0 1 1 * 1 0 0. . c. . 0 1 1 * 0 0 0. . d. . 0 1 1 * 0 0 0. . e. . 0 0 1 * 0 0 0. . a

10) Md. T : test se a=b, caso a>b dopo aver cancellato un 1 da b e e anche da a, avro’la situazione in rosso, vado a fare b-1, al solito cerco zero dopo gli uni di b, qui trovo subito zero, torno a sinist. in stato c per cancellare un 1 di b, ma trovo * (non 1) caso b=0; se in c trovo asterisco, passo in stato f c * f * - ; ora so che il dato b e' zero devo controllare se anche a=0, passo in stato f, vado a sinistra sul dato a: se in stato f trovo un uno a sinistra di * 44. . 0 1 1 * 1 0 0. . a. . . 0 1 1 * 0 0 0. . e. . 0 0 1 * 0 0 0. . a. . 0 0 1 * 0 0 0. . b. . 0 0 1 * 0 0 0. . c. . 0 0 1 * 0 0 0. . f. . 0 0 > * 0 0 0. . h

10) Md. T : test se a=b, caso a==b a * b * + ; situazione iniziale b 1 + ; scorri b a destra b 0 c 0 - ; quando trovi 0 in b, ; vai in stato c e c 1 d 0 - ; fai b-1 se possibile d 1 - ; scorri a sinistra dopo b-1 d * - ; scavalca asterisco in mezzo d 0 e 0 + ; fino allo zero a sin. di a e 1 a 0 + ; fai a-1 se possibile a 1 + ; scorri uni di a fino * ; restano da vedere i casi finali: ; se dopo fatto b-1 trovo che a=0, cioe' e * h < 0 ; scrive risultato a<b c * f * - ; se cerco di fare b-1, trovo ; * allora b=0, vado controllare a : f 0 h = 0 ; trovo 0 a sin dell’*: anche a=0! f 1 h > 0 ; c’e’ 1 a sin. di *: allora a>0, b=0 si osservi che le quintuple con la coppia s, q= f * a 0 c 0 e 0 non possono presentarsi 45. . 0 1 * 1 0 0. . a. . . 0 1 * 0 0 0. . e. . 0 0 * 0 0 0. . a. . 0 0 * 0 0 0. . b. . 0 0 * 0 0 0. . c. . 0 0 * 0 0 0. . f. . 0 = * 0 0 0. . h

10) Md. T : test se a=b, caso a<b a * b * + ; situazione iniziale b 1 + ; scorri b a destra b 0 c 0 - ; quando trovi 0 in b, ; vai in stato c e c 1 d 0 - ; fai b-1 se possibile d 1 - ; scorri a sinistra dopo b-1 d * - ; scavalca asterisco in mezzo d 0 e 0 + ; fino allo zero a sin. di a e 1 a 0 + ; fai a-1 se possibile a 1 + ; scorri uni di a fino * ; resta da vedere i casi finali: ; se dopo fatto b-1 trovo che a=0, cioe' e * h < 0 ; scrive risultato a<b c * f * - ; se cerco di fare b-1, trovo ; * allora b=0, vado controllare a : f 0 h = 0 ; trovo 0 a sin dell’*: anche a=0! f 1 h > 0 ; c’e’ 1 a sin. di *: allora a>0, b=0 46. . 0 1 * 1 1 0. . a cancella uno: dopo b-1, a-1 ho: . . 0 0 * 1 0 0. . a e ripeti. . 0 0 * 1 0 0. . b. . 0 0 * 1 0 0. . c. . 0 0 * 0 0 0. . d. . 0 0 * 0 0 0. . e. . 0 0 < 0 0 0. . h

10) Md. T : test se a=b; rivediamo le quintuple: a * b * + ; situazione iniziale b 1 + ; scorri b a destra in cerca dello zero di fine b b 0 c 0 - ; quando trovi 0 dopo b, vai in stato c, vai a sin c 1 d 0 - ; se trovi 1 allora fai b-1 e poi in stato d, a sin d 1 - ; dopo b-1 scorri a sinistra gli 1 di b e/o di a d * - ; scavalca asterisco in mezzo d 0 e 0 + ; fino allo zero a sinistra di a e 1 a 0 + ; c'e' almeno un 1 di a, faccio a-1 se possibile a 1 + ; scorri a destra gli 1 di a fino * ; casi finali: ; (e, *) e'il caso a=0 dopo fatto b-1 cioe': e * h < 0 ; dopo b-1 e senza a-1, scrive risultato a<b ; (c, *) e'il caso b=0, si deve controllare se a e'zero o no: c * f * - ; devo controllare a: in stato f (b=0) ho: f 0 h = 0 ; trovo 0 a sin dell’*: anche a=0, a e b uguali ! f 1 h > 0 ; c’e’ un 1 a sin. di *: allora a>0, b=0, quindi a>b ; non tutte le coppie (q, s) sono presenti: le coppie ; (q, s) = (f *), (a 0), (c 0), (e 0) non possono presentarsi ; si lascia come esercizio la verifica di questo. . . 47

esercizio 11) dato un numero n calcolare il valore 2*n 48

esercizio 11) dato un numero n calcolare il valore 2*n dobbiamo prima specificare la codifica, ad es. : 000 A 111 B 000000 a dato n=3; per ogni 1 del dato n scrivo due 1 a destra di B: 000 A 011 B 1100000 a 000 A 001 B 11110000000 a 000 A 000 B 11111100000 h si lascia allo studente l'esercizio. . . 49

cosa si puo’ fare con una m. d. T. abbiamo cosi’ verificato che esistono m. di T. per fare n+1 fare test se a=b? fare copia del valore di a in un altra parte. . . sono le operazioni fondamentali per fare aritmetica intera. . non e’ difficile definire m. d. T. per fare altri “conti” vedremo che con le Md. T si possono risolvere molti problemi anche piu' complicati. . . 50

esercizi suggeriti 1) m. d. T per fare la somma di due numeri A e B: ad es. con il dato (A e B in unario, delimitati da x, y, w) : . . . x 1 1 1 y 1 1 w 0 0 0 0. . . a ottenere il risultato: . . . x 0 0 0 y 0 0 w 1 1 1 0 0. . . h (i dati originali qui non vengono conservati) 51

esercizi suggeriti 2) macchina per fare il prodotto di due numeri ad es. con il dato A=3, B=2 codificato ad es. con: . . x 111 y 11 w 0000000. . . a ottengo il risultato: . . x 000 y 00 w 111111111 z 0000. . . h 52

cont. esercizi da fare 3) macchina per compattare una stringa di zeri e uni, delimitata dal simbolo x. Ad es. dato. . . x 1 1 1 0 1 0 1 1 0 0 1 x 0 0. . . a ottengo il risultato (le celle su nastro non sono numerate!) : . . . x 1 1 1 1 x 0 0. . . h nota che una cella della memoria a nastro esterna non puo' "sparire", ma puo' solo cambiare valore ! 53

cont. esercizi da fare 54 4) macchina azzera le coppie di uni sul nastro esterno; ad esempio a partire da un nastro del tipo: . . . x 1 1 1 0 0 1 x 0 0. . . a ottengo : . . . x 0 0 1 0 0 0 0 1 x 0 0. . . h

cont. esercizi da fare 5) macchina che conta le stringhe contenenti una coppia di zeri, ad es. dal nastro dato: . . x 1 1 1 x 0 0 0 x 0 1 0 y 0 0 0. . a produce: . . . y 1 1 z 0 0 0. . h 55

cont. esercizi da fare 56 6) macchina somma due numeri in base dieci; ad esempio a partire dal nastro. . x 0 9 8 x 1 2 3 x 0 0 0. . produce il nastro: . . x 0 9 8 x 1 2 3 x 2 2 1 x (nota: per calcolare a+b con a, b codificati in base 10 si usi il procedimento ripeti a<-a+1; b<-b-1 fino_a_che b=0 )

cont. esercizi da fare 57 7) macchina che cerca una stringa uguale ad una stringa data, tutte le stringhe sono composte da soli 0 e 1 e sono delimitate da un simbolo x. . z 0 0 z 1 1 x 1 0 x 0 0 x. . a la stringa data 0 0 sta tra due z, ed e' uguale alla quarta stringa dopo la z; il problema dovra' essere scomposto in problemi piu' semplici; lo stato interno (o la sequenza di stati interni) ricordera' il simbolo letto dopo z, che sara' ad es sostituito con un simbolo diverso, ad es. 0 diventa a, 1 diventa b, di seguito in stato q dopo avere riconosciuto che il primo simbolo dopo x e' uguale al 1. o simbolo dopo il 3. o x

cosa si puo’ fare con una m. d. T. abbiamo cosi’ verificato che esistono m. di T. che sanno risolvere alcuni problemi : n+1, test se a=b? , (si potrebbe vedere anche le operazioni di somma a+b, e prodotto a*b ), copia del valore di a in un altra parte (a : = b). . . queste sono alcune delle operazioni fondamentali per fare aritmetica intera. . non e’ difficile definire m. d. T. per fare altri “conti” 58

59 cosa si puo’ fare con una m. d. T. ?

si puo' simulare un calcolatore con una Md. T ? 60 si puo' dimostrare che e' possibile simulare un calcolatore digitale con una M. di T. ; in particolare, si possono costruire Md. T per simulare i singoli componenti del calcolatore, come la memoria centrale, l' unita' centrale, una memoria a disco. . . vediamo un cenno sul problema di simulare la memoria centrale del calcolatore con una Md. T

si puo' simulare un calcolatore con una Md. T ? 61 problema: simulare la memoria centrale del calcolatore con una Md. T la memoria centrale del calcolatore e' molto diversa dalla memoria a nastro di una Md. T; la memoria centrale e' un dispositivo HW fatto di celle di memoria (di formato fisso) ciascuna con un indirizzo ed e' in grado di fare due operazioni: memorizza D e leggi D "scrivi un dato D nella cella di memoria di indirizzo A" "leggi un dato D dalla cella di memoria di indirizzo A"

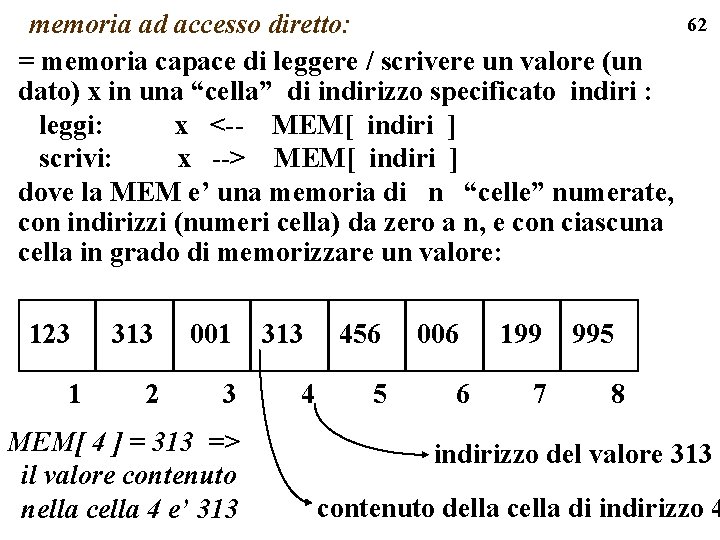
memoria ad accesso diretto: = memoria capace di leggere / scrivere un valore (un dato) x in una “cella” di indirizzo specificato indiri : leggi: x <-- MEM[ indiri ] scrivi: x --> MEM[ indiri ] dove la MEM e’ una memoria di n “celle” numerate, con indirizzi (numeri cella) da zero a n, e con ciascuna cella in grado di memorizzare un valore: 123 1 313 001 2 3 MEM[ 4 ] = 313 => il valore contenuto nella cella 4 e’ 313 4 456 5 006 6 199 7 62 995 8 indirizzo del valore 313 contenuto della cella di indirizzo 4

una memoria a indirizzo? ma la m. di T. non lo e' ! La memoria nastro esterno di una macchina di Turing e’ composta da celle adiacenti non numerate, l'accesso ad una cella e' sequenziale, passando prima per tutte le celle intermedie. . per individuare un dato si introducono dei simboli speciali di marcatura (“delimitatori”), ad es. : “cancella il dato che sta tra due celle contenenti w. . . 0 0 0 w 1 1 1 w 0 0. . . ^ ^ 63

una memoria a indirizzo Es: una Md. T con un po'di dati sul nastro esterno, separati dal simbolo x, 00 x 01011 x 00 x 111 x 1001 x 0101 x 00 a (=posizione testina e stato interno) allora per arrivare al 4. o dato 1001 devo scorrere (leggere / riscrivere) i primi tre; . . . ma: una Md. T puo' simulare la memoria a indirizzi con un sistema di codifica del tipo seguente (A, B, C sono simboli delimitatori) : . . . A 01011 B 1001001000111 C. . . dove la parte 01011 tra A e B e' l'indirizzo, e la parte 1001001000111 tra B e C e' il dato 64

continua la memoria a indirizzo 65 in particolare, vediamo ora una m. d. T. che simula il comportamento di una memoria con celle numerate, individuabili dal numero di cella di memoria o indirizzo: cioe’ un “dispositivo” che sa fare le due operazioni di base per ogni dispositivo di memoria: scrivi (registra) in memoria un dato DDD all’ indirizzo III leggi dalla memoria il valore che c’e’ all’indirizzo III

continua la memoria a indirizzo 66 m. d. T. che simula una memoria con “celle” numerate, cioe’ con memoria con dati accessibili specificando un indirizzo: “azzera il dato nella “cella” di numero 22”: date tre “celle” di memoria di indirizzo 21, 22 e 23 (con valori 4, 1 e 0 rispett. ). 2 2 x 2 1 w 4 w 2 2 w 1 w 2 3 w 0. . . ^ ^ ^valore=1, indirizzo=22 dopo l’istruzione detta avremo: . 2 2 x 2 1 w 4 w 2 2 w 0 w 2 3 w 0. . . ^ riportiamo di seguito solo parte della soluzione; nota: per selezionare il dato giusto devo trovare quale indirzzo e' uguale all'indirizzo dato 22;

continua la memoria a indirizzo 67 prima parte del problema della memoria a indirizzo: dato un insieme di stringhe di tre caratteri separate da x e delimitate da y trovare la stringa uguale alla stringa data: . . y 0 1 0 x 0 1 1 x 0 1 0 x 1 0 1 y. . ^^^ ||| dato str. a valore coincid. procedimento: esamino i caratteri della stringa data uno dopo l’altro, ricordando sia su nastro sia con uno stato di scorrimento diverso se ho letto un 0 oppure un 1: cerco poi a destra la prima stringa non ancora esaminata e vedo se ha gli stessi caratteri: se si, e’ la stringa cercata, se no, continuo (fino al delimitatore delle stringe y)

m. d. T. “memoria ad accesso diretto” 68 formato codifica della memoria con indirizzi e dati a tre cifre: y 010 x 000111 x 010101 x 011001 x a si puo' fare una Md. T per rispondere alla domanda: qual e’ il valore del dato di numero (o di indirizzo) 010? (qui e’ 101) con il procedimento: 1) dato un indirizzo i (010) cerca tra gli indirizzi un kj tale che kj = i, (m. d. T. cerca stringa=), e ho ad es y 010 x. AAABBBx. ABA 101 x 011001 x a 2) poi copia il dato (la stringa 1 0 1) al posto dell’indirizzo i: y. BABx. AAABBBx. ABABABx 011001 x i

memoria a indirizzi su supporto fisico a memoria sequenziale 69 negli anni 60 sono stati realizzati sistemi di memoria a nastro magnetico formattato a zone di memoria di ampiezza fissa e con indirizzo registrato accanto il dato; il sistema era in grado di trovare il dato di indirizzo k cercando su nastro (con ricerca sequenziale) la zona con indirizzo k e quindi il dato corrispondente (memoria associativa, ogni dato ha registrato anche l'indirizzo che lo individua (o chiave) ) questo sistema non ha avuto successo. . .

una macchina di Turing "programmabile" 70 tutte le M. di T "sanno" (per definizione) eseguire solo un algoritmo, cioe' quello "prefissato" nella memoria delle quintuple (che e' a sola lettura, non modificabile); e quindi una M di T ha UN programma; ma: e' possibile codificare una qualunque macchina di Turing (quintuple, nastro, memoria dello stato, posizione testina) su un nastro esterno di una particolare m. d. T. , che chiameremo m. d. T Universale; si puo' costruire un insieme di quintuple per realizzare le azioni richieste per una qualunque m. d. T. , cioe' l'algoritmo di imitazione a questo punto abbiamo una m. d. T. "programmabile",

cont. “U”, una m. d. T. speciale. . . 71 la m. d. T. “U” o “Universale” e’ una macchina che in effetti sa eseguire un solo algoritmo, (come del resto ogni m. d. T. , per definizione) e cioe’ la procedura di imitazione della m. d. T. “X” che e’ codificata sul suo nastro: “dato stato q corrente e simbolo s corrente [di X!] codificati subito a destra della cella y sul nastro [di U!] cerca tra le quintuple [di X] codificate su nastro [di U] quella che comincia con la coppia q, s uguale; a questo punto sostituisci q 1 al posto di q [sul nastro U, a dest. di y] e s 1 al posto di M [sul nastro di U, dove prima era s], e

osservazione per chi e' interessato all'argomento vedere ad es. M. L. Minsky: "Computation: Finite and Infinite Machines", Prentice Hall 1967, cap. 6, 7, 8. , questi argomenti saranno ripresi in altri corsi di seguito e’ riportata la versione grafica di una m. d. T. universale, solo a titolo di curiosita' !! 72

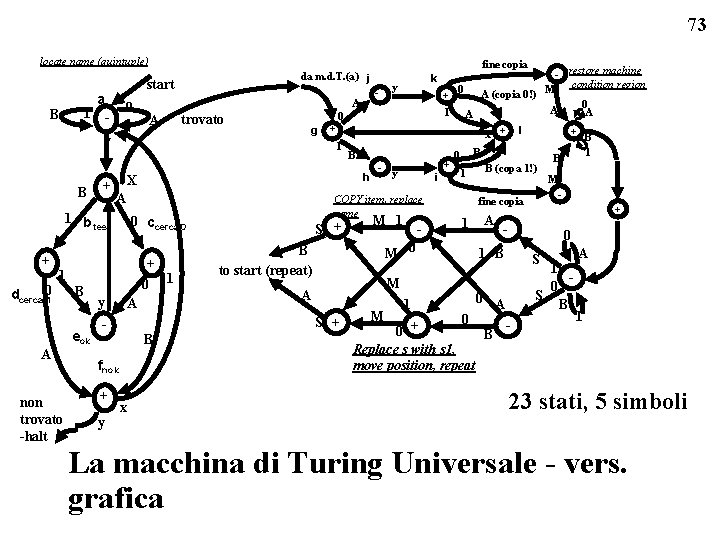
73 locate name (quintuple) start a 0 1 - B trovato y B + + dcerca 01 eok A non trovato -halt A A B fnok y S + x 0 A (copia 0!) B - + l y i M 1 - B to start (repeat) M A M 1 1 B (copa 1!) A B M + - 0 1 B 0 A B 1 - fine copia 1 0 A + B 0 - restore machine condition region M A A x + M 0 S + - + COPY item, replace name 0 ccerca 0 y y 1 h + 0 1 + + X 1 B g k 0 1 1 b test - A A fine copia da m. d. T. (a) j S 0 0 + B Replace s with s 1, move position, repeat 1 0 S B A 1 23 stati, 5 simboli La macchina di Turing Universale - vers. grafica

m. d. T e algoritmi segue un discorso generale sulle M. d. T. , sull'applicabilita', sugli algoritmi e sulle funzioni effettivamente calcolabili 74

applicabile dato) ( md. T applicabile ad un definizione di applicabile diremo che una md. T “T” e’ applicabile al dato D se fatta partire T con un nastro su cui e’ codificato D da’ luogo ad una computazione che finisce in un numero finito di passi, ovvero T e’ applicabile a D se produce in un numero finito di passi un risultato R. 75

calcolabile 76 Un algoritmo puo’ essere pensato come una funzione f che a partire da dei dati (*) produce dei risultati (*) quindi come: y = f(x) con x (dato) e y(risultato) interi, diremo che f e’ T calcolabile se esiste una m. d. T. T tale che fatta partire con un nastro su cui e’ codificato x produce in un numero finito di passi un nastro su cui e’ codificato y; diremo che f e’ P calcolabile se esiste un Programma C++ P tale che fatto partire con il dato x produce in un numero finito di passi il risultato y; __________________________________ (*)n. b: un dato (ad es. formato da 1000 numeri in virgola mobile di 10 cifre

md. T “T” <=> f(intero) -> intero parziale 77 diremo che f(x)->y e’ T (o P) calcolabile se esiste una m. d. T. (o un programma C++) applicabile a x e che produce (in un numero finito di passi) il risultato y; nota: una md. T “T” puo’ essere applicabile ad alcuni dati, che chiameremo Da = insieme dati per cui T si ferma, Da = {d, T(d) si ferma}, ma non applicabile ad altri: Dn = ins. dati per cui T non ferma: Dn = {d, T(d) non si ferma}: Associo ad ogni dato d della md. T “T” un intero k -> l’insieme degli interi I risulta suddiviso in due sottoinsiemi, Ka che corrisponde ai dati Da (su cui T e’ applicabile), e

le m. d. T sono meno potenti del C++? Si puo’ dimostrare che l’insieme delle funzioni T calcolabili, coincide con l’insieme delle funzioni C++ calcolabili, cioe’ per ogni md. T esiste un programma C++ corrispondente, e viceversa. . . ovvero: i due formalismi sono altrettanto potenti! cioe' se si puo' risolvere un problema con il linguaggio C++ (con un calcolatore digitale) lo stesso problema si puo' risolvere con il formalismo delle Md. T (e in particolare i diversi linguaggi di programmazione procedurali (o imperativi) hanno la stessa potenza: quello che si puo' risolvere in Visual Basic si puo' 78

le m. d. T sono meno potenti del C++? Si puo’ dimostrare che per ogni md. T esiste un programma C++ corrispondente, e viceversa. . . Definiamo una procedura effettivamente computabile una procedura che si puo’ esprimere con una m. d. T. oppure con un programma C++ algoritmo = procedura effettivamente computabile = = md. T ( tale che si ferma !! ) = programma C++ ( tale che si ferma !! ) (oppure con uno dei molti formalismi definiti da vari autori, o con uno dei moltissimi linguaggi di programmazione). 79

tesi di Church: linguaggi di programmazione. . . Ada, Basic, C++, Cobol, Java, Logo, Euclid, Lisp, Modula, Oberon, Pascal, PL / I, Smalltalk, . . . e altri 10000 linguaggi. . . formalismi. . . di Church, di Kleene, di Markov, di Mc. Carthy, di Post, di Turing, . . . ogni algoritmo si puo' scrivere in uno qualunque di questi formalismi : tesi di Church: sono tutti formalismi di pari potenza (ipotesi fondamentale della teoria degli algoritmi) 80

tesi di Church: i formalismi definiti finora per scrivere algoritmi sono tutti formalismi di pari potenza (ipotesi fondamentale della teoria degli algoritmi) per i formalismi finora costruiti e’ stato dimostrato che l’insieme delle funzioni calcolabili da ciascuno di essi e’ lo stesso ( ma - non e’ stato dimostrato che non esiste un formalismo piu’ potente ) 81

limiti infine, ancora un dubbio: . . . cosa si puo’ fare con una m. d. T? ovvero: cosa si puo' risolvere con un algoritmo? si puo' formulare un problema in modo che si possa cercare di risolverlo per via algoritmica (ad es. con un programma in C++) e poi scoprire che non si puo' risolvere? esistono problemi non risolubili per via algoritmica? esistono problemi per cui non si potra' mai scrivere un programma che li risolva? 82

limite. . . cosa si puo’ fare con una m. d. T? 83 si puo' dimostrare che esistono problemi (esprimibili in forma adatta per una m. d. T. /un progr C++) non risolubili per via algoritmica, ovvero per i quali non esiste una m. d. T. (o un programma C++) osservazione molto semplice: 1) si noti che l’insieme delle funzioni da intero F i ( N ) -> N { dove ogni F i fa corrispondere m, ad un generico numero intero k un (altro) numero intero se F i e’ definita su k, altrimenti non fa corrispondere nulla } [ -->> quante sono le possibili coppie (intero - intero) ? ] cioe’ di TUTTE le possibili funzioni che fanno corrispondere un numero intero m ad un altro

per ogni md. T c'e' una f(i) , ma per ogni f(i) c'e' md. T ? e' sufficiente osservare che l’insieme di TUTTE le funzioni da intero F i ( N ) -> N non e’ numerabile, mentre: l’ insieme delle m. d. T. (o dei progr. C++) e’ numerabile quindi: 84 la gran parte delle funzioni da intero NON sono esprimibili con una m. d. T. , ovvero gran parte delle f(i)>i non ha una md. T corrispondente! molti problemi NON hanno soluzione algoritmica; vediamo un problema non risolubile per via algoritmica.

problema dell’ arresto (halting problem) 85 dato un programma qualunque (data una m. d. T. qualunque) con un dato iniziale fissato (una situazione su nastro) ci si chiede se solo analizzando il programma / la md. T - (senza esecuzione) e’ possibile sapere se il processo di calcolo che avra’ luogo - fatto partire il calcolatore (fatta partire la m. d. T) su quel dato produrra’ un risultato entro un numero finito di passi ? cioe’ se si fermera’? cioe’ --

problema dell’ arresto (halting problem) problema: “data una md. T X e un nastro dati D, se faccio partire X con i dati D la md. T X si fermera’ dopo un numero finito di passi (cioe’ X e’ applicabile a D)? . . . 000313008 x 82 y 1000. . . (a, 0, . . . ) quintuple f (a, 1, . . . ) della (dati D su nastro) (b, 8, . . . ) md. T. X risposta “ingenua”: . . . faccio partire il programma: se dopo un po’ si ferma allora la m. d. T. X e’ applicabile a quei dati D, se non si ferma allora X non e’ applicabile a D. ma. . . non e’ una buona risposta! in effetti non posso sapere se una Md. T che lavora da 75301 giorni magari si ferma dopo il 75302. mo giorno. . . 86

problema dell’ arresto (halting problem) 87 problema: “data una md. T X e un nastro dati D, se faccio partire X con i dati D la md. T X si fermera’ dopo un numero finito di passi (cioe’ e’ X applicabile a D)? si puo’ avere la risposta solo ispezionando, analizzando la m. d. T. (chiamiamola md. T”X”) ed i relativi dati ? esprimiamo il problema cosi’: “ dati una md. T X e un nastro dati D, e’ possibile sapere - solo analizzando X e D, senza far partire la macchina se la md. T X, fatta partire con i dati D, si fermera’ dopo un numero finito di passi ? (cioe’ se X e’ applicabile a D ? ) risposta: si puo' dimostrare che non e’ possibile

problema dell’ arresto (halting problem) 88 quindi : dato un generico programma P con i suoi dati D non e’ possibile determinare ( con un programma “magico” G ) se il programma P e’ applicabile al dato generico D quindi: il problema dell’arresto non e’ risolubile per via algoritmica ovvero: non c’e’ una procedura effettiva (un algoritmo, una md. T, un programma C++. . . ) per stabilire se una procedura X e’ realmente effettiva (algoritmo che si ferma in un numero finito di passi) oppure no. ovvero: non e’ possibile costruire un programma G (un compilatore magico) tale che esso solo leggendo il testo di un generico programma X risponda: si’, questo programma funziona, oppure no, questo programma

problema dell’ arresto (halting problem) 89 ma attenzione - se e’ vero che: dato un generico programma P non e’ possibile determinare con un programma “magico” G se il programma P e’ applicabile ad un dato generico D cioe’ se si fermera’ questo non significa che non esistano particolari tipi di programmi / dati per i quali invece esiste la soluzione ovvero: il problema dell’arresto per un programma qualunque applicato ad un dato qualunque e’ troppo generale per avere una soluzione algoritmica, ma. . . esistono casi particolari per i quali esiste una soluzione algoritmica.

problema dell’ arresto (halting problem) 90 nota: il fatto che esistono problemi non risolubili per via algoritmica pone un limite a quello che si puo’ fare con gli algoritmi (e con i calcolatori); questo tipicamente succede per problemi di natura troppo generale; rimane da stabilire di volta in volta se un particolare problema e’ risolubile. . . sara’ oggetto del nostro corso lo studio della soluzione di alcuni problemi abbastanza semplici e ben delimitati. . .

riassumiamo alcuni concetti: procedura di calcolo=lista di istruzioni=progr. C++=md. T: stato iniziale: nastro con dati D, stato q e posiz. testina. istruzioni: quintuple; md. T applicabile a D se si ferma; processo di calcolo = procedimento di calcolo = insieme degli stati di una md. T, dal primo (stato iniziale, con il dato di partenza) all’ultimo (stato finale, con il risultato) 91

riassumiamo alcuni concetti: algoritmo = discrizione completa, eseguibile, finita, non ambigua di un procedimento di calcolo che a partire da dei dati D da’ luogo ad un procedimento di calcolo finito, che in un numero finito di passi produce un risultato R. algoritmo = una md. T X che a partire da dei dati D si ferma e produce un risult. R in un n. ro finito di passi (X e’ applicabile a D); algoritmo = una md. T applicabile = procedura effettivamente computabile = un programma che produce un risultato in un numero finito di passi 92

93 e con questo concludiamo questo capitolo sugli algoritmi e sulle macchine di Turing

94 fine