Contents Vocabulary Click on a topic to go

Contents • Vocabulary Click on a topic to go to that section. • Translating Between Words and Expressions • Tables and Expressions • Evaluating Expressions • The Distributive Property • Combining Like Terms

Vocabulary Return to Table of Contents

What is a Constant? A constant is a fixed value, a number on its own, whose value does not change. A constant may either be positive or negative. Example: 4 x + 2 In this expression 2 is a constant. click to reveal

What is a Variable? A variable is any letter or symbol that represents a changeable or unknown value. Example: 4 x + 2 In this expression x is a variable. click to reveal

What is a Coefficient? A coefficient is the number multiplied by the variable. It is located in front of the variable. Example: 4 x + 2 In this expression 4 is a coefficient. click to reveal

If a variable contains no visible coefficient, the coefficient is 1. Example 1: x + 7 is the same as 1 x + 7 Example 2: - x + 7 is the same as -1 x + 7

1 In 2 x - 12, the variable is "x" True False

2 In 6 y + 20, the variable is "y" True False

3 In 3 x + 4, the coefficient is 3 True False

4 What is the constant in 7 x - 3? A 7 B x C 3 D -3

5 What is the coefficient in - x + 3? A none B 1 C -1 D 3

6 x has a coefficient True False

What is an Algebraic Expression? An Algebraic Expression contains numbers, variables and at least one operation. Example: 4 x + 2 is an algebraic expression. ×

What is an Equation? An equation is two expressions balanced with an equal sign. Example: 4 x + 2 = 14 Expression 1 Expression 2

What is the difference between an expression and an equation? An expressions contains: • numbers • variables • operations Click to reveal An equation contains: • numbers • variables • operations • an equal sign Click to reveal

Translating Between Words and Expressions Return to Table of Contents

List words that indicate addition

List words that indicate subtraction

List words that indicate multiplication

List words that indicate division

Be aware of the difference between "less" and "less than". For example: "Eight less three" and "Three less than Eight" are equivalent expressions. So what is the difference in wording? Eight less three: Three less than eight: 8 -3 When you see "less than", you need to switch the order of the numbers.

As a rule of thumb, if you see the words "than" or "from" it means you have to reverse the order of the two items on either side of the word. Examples: • 8 less than b means b - 8 • 3 more than x means x + 3 • x less than 2 means 2 - x click to reveal

The many ways to represent multiplication. . . How do you represent "three times a"? (3)(a) 3 a 3 a The preferred representation is 3 a When a variable is being multiplied by a number, the number (coefficient) is always written in front of the variable. The following are not allowed: 3 xa. . . The multiplication sign looks like another variable a 3. . . The number is always written in front of the variable

Representation of division. . . How do you represent "b divided by 12"? b ÷ 12 b ∕ 12 b 12

When choosing a variable, there are some that are often avoided: l, i, t, o, O, s, S Why might these be avoided? It is best to avoid using letters that might be confused for numbers or operations. In the case above (1, +, 0, 5)

TRANSLATE THE WORDS INTO AN ALGEBRAIC EXPRESSION Three times j Eight divided by j + j - j less than 7 5 more than j 4 less than j ÷ 0 2 4 6 8 1 3 5 7 9

Write the expression for each statement. Then check your answer. The sum of twenty-three and m 23 + m

Write the expression for each statement. Then check your answer. Twenty-four less than d d - 24

Write the expression for each statement. ***Remember, sometimes you need to use parentheses for a quantity. *** Four times the difference of eight and j 4(8 - j)

Write the expression for each statement. Then check your answer. The product of seven and w, divided by 12 7 w 12

Write the expression for each statement. Then check your answer. The square of the sum of six and p (6 + p) 2

7 The quotient of 200 and the quantity of p times 7 A 200 7 p B 200 - (7 p) C 200 ÷ 7 p D 7 p 200

8 35 multiplied by the quantity r less 45 A 35 r - 45 B 35(45) - r C 35(45 - r) D 35(r - 45)

9 Mary had 5 jellybeans for each of 4 friends. A 5+4 B 5 -4 C 5 x 4 D 5÷ 4

10 If n + 4 represents an odd integer, the next larger odd integer is represented by A n+2 B n+3 C n+5 D n+6

11 a less than 27 A 27 - a a B 27 C a - 27 D 27 + a

12 If h represents a number, which equation is a correct translation of: “Sixty more than 9 times a number is 375”? A 9 h = 375 B 9 h + 60 = 375 C 9 h - 60 = 375 D 60 h + 9 = 375

Tables and Expressions Return to Table of Contents

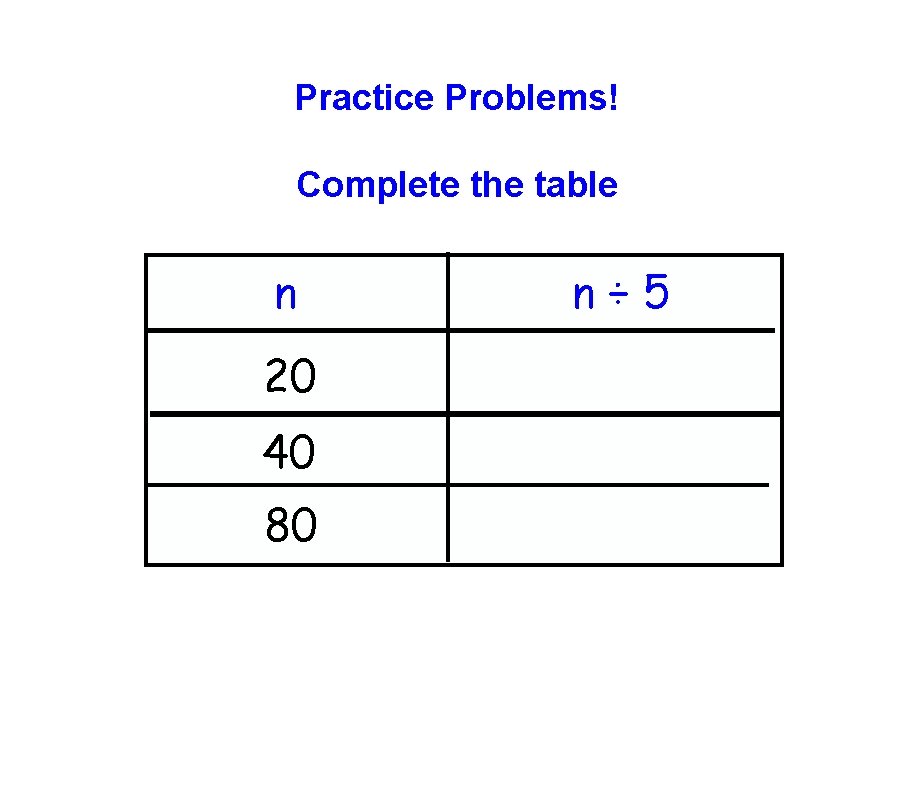
Practice Problems! Complete the table n 20 40 80 n÷ 5

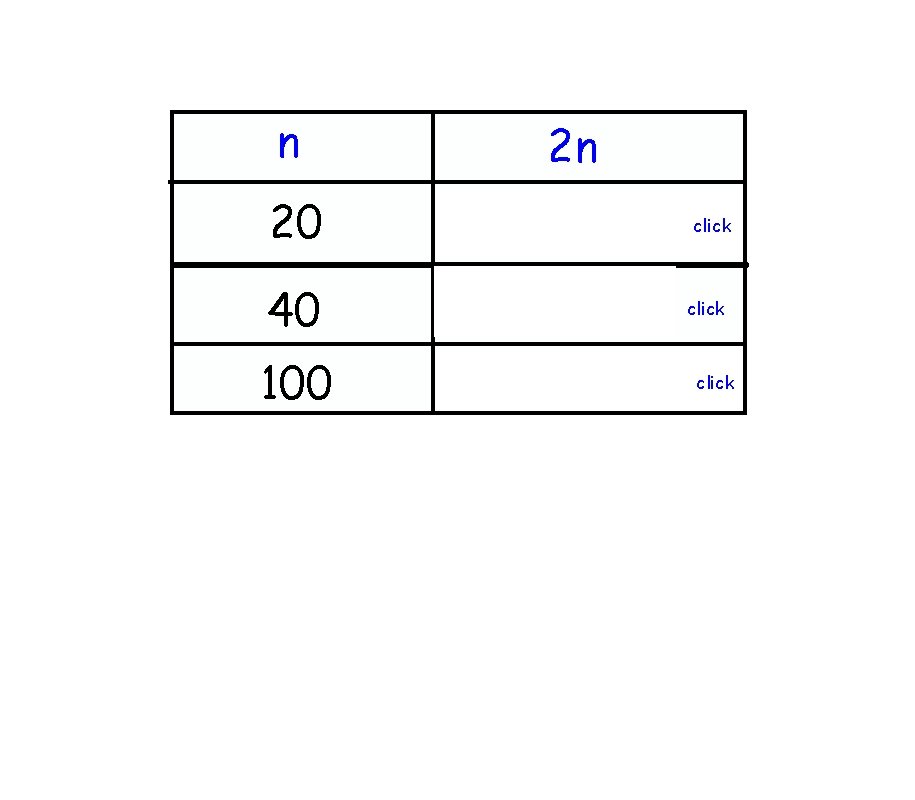
n 2 n 20 40 40 80 100 200 click

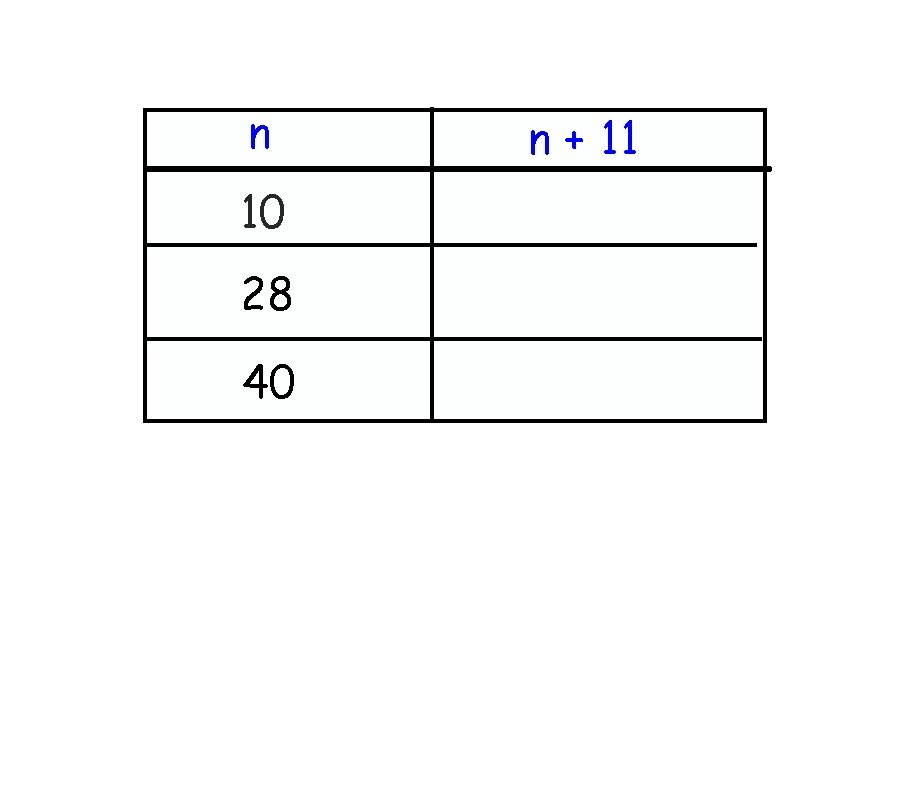
n 10 28 40 n + 11

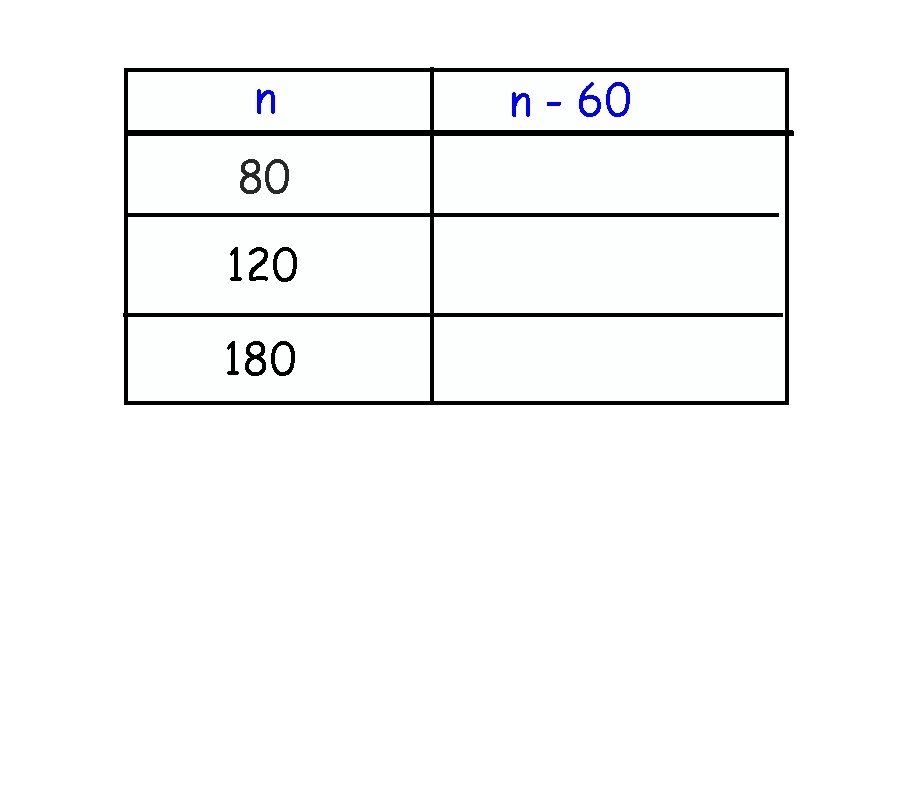
n 80 120 180 n - 60

Mary's age is twice the age of Jack. Use that fact to complete the table. Jack's Age Mary's Age 12 24 14 28 24 48 a 2 a click Can you think of an expression containing a variable which determines Mary's age, given Jack's age?

The manager of the department store raised the price $15 on each video game. Original price Price after mark up $100 $115 $55 $70 $38 $53 x click x + 15 Can you find an expression that will satisfy the total cost of the video game if given the original price?

A parent wants to figure out the differences in grade level of her two sons. The younger son is two years behind the older one in terms of grade level. older son's grade level 6 10 2 g younger son's grade level 4 th grade 8 th grade Kindergarten g - click 2 Write an expression containing a variable which satisfies the difference in grade level of the two boys.

The tire manufacturer must supply four tires for each quad built. Determine the number of quads that can be built, given then number of available tires. # of tires # of Quads 20 5 40 10 100 25 t t ÷ 4 or t/4 Can you determine an expression containing a variable for the number of quads built based upon the amount of tires available?

13 Bob has x dollars. Mary has 4 more dollars than Bob. Write an expression for Mary's money. A 4 x B x-4 C x+4 D 4 x + 4

14 The width of the rectangle is five inches less than its length. The length is x inches. Write an expression for the width. A 5 -x B x-5 C 5 x D x+5

15 Frank is 6 inches taller than his younger brother, Pete's height is P. Write an expression for Frank's height. A 6 P B P+6 C P-6 D 6

16 The dog weighs three pounds more than twice the cat. Write an expression for the dog's weight. Let c represent the cat's weight. A 2 c + 3 B 3 c + 2 C 2 c + 3 c D 3 c

17 Write an expression for Mark's test grade. He scored 5 less than Sam. Let x represent Sam's grade. A 5 -x B x-5 C 5 x D 5

18 Tim ate four more cookies than Alice. Bob ate twice as many cookies as Tim. If x represents the number of cookies Alice ate, which expression represents the number of cookies Bob ate? A 2 + (x + 4) B 2 x + 4 C 2(x + 4) D 4(x + 2)

Evaluating Expressions Return to Table of Contents

Steps for Evaluating an Expression: 1. Write the expression 2. Substitute the values given for the variables (use parentheses!) 3. Simplify the Expression click to reveal Remember Order of Operations! Write - Substitute - Simplify

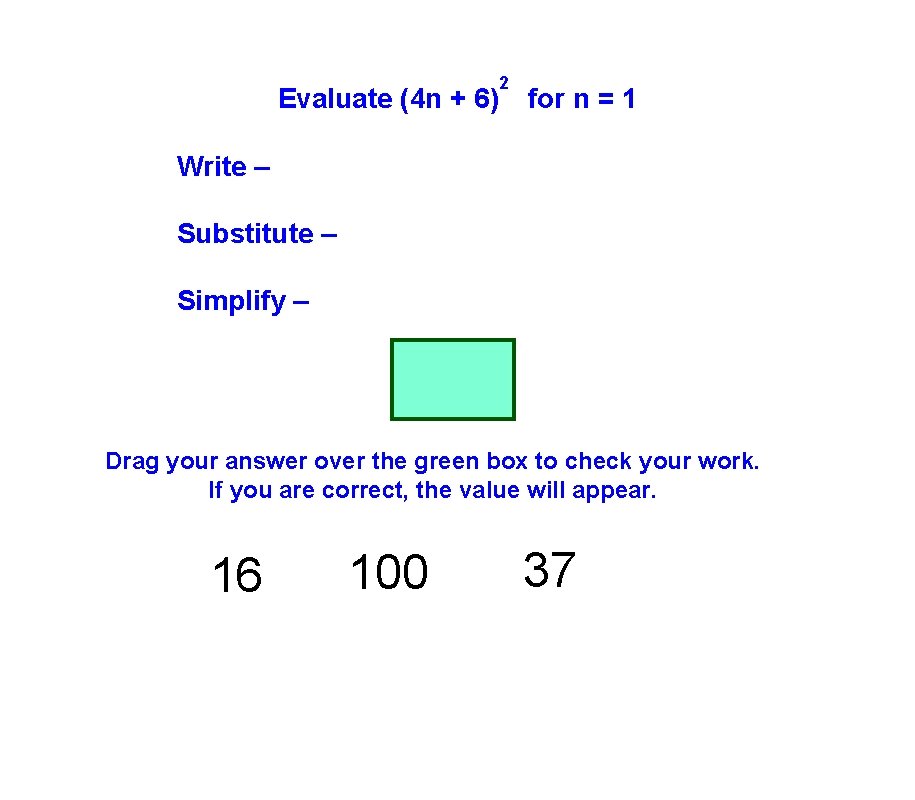
Evaluate (4 n + 6) 2 for n = 1 Write – Substitute – Simplify – Drag your answer over the green box to check your work. If you are correct, the value will appear. 16 100 37

Evaluate the expression 4(n + 6) 2 for n = 2 Write – Substitute – Simplify – Drag your answer over the green box to check your work. If you are correct, the value will appear. 20 32 256

Let x = 8, then use the magic looking glass to reveal the correct value of the expression 12 x + 2 106 3 104 116 108 114 118 128 130

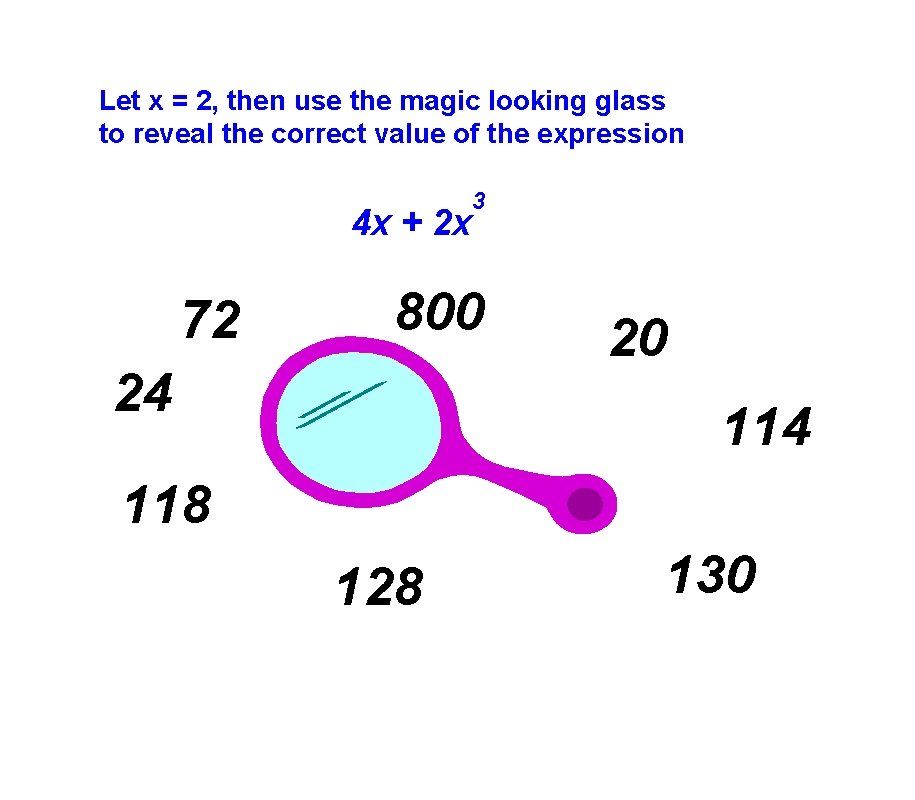
Let x = 2, then use the magic looking glass to reveal the correct value of the expression 4 x + 2 x 72 3 800 24 20 114 118 128 130

19 Evaluate 3 h + 2 for h = 3

20 2 Evaluate 2(x + 2) for x = -10

21 2 Evaluate 2 x for x = 3

22 Evaluate 4 p - 3 for p = 20

23 Evaluate 3 x + 17 when x = -13

24 Evaluate 3 a for a = -12 9

25 Evaluate 4 a + a for a = 8, c = -2 c

26 2 If t = -3, then 3 t + 5 t + 6 equals A -36 B -6 C 6 D 18

27 What is the value of the expression |− 5 x + 12| when x = 5? A -37 B -13 C 13 D 37

28 3 0 2 What is the value of the expression (a + b ) when a = − 2 and b = 4? A 64 B 49 C -49 D -64

29 Evaluate 3 x + 2 y for x = 5 and y = 1 2

30 Evaluate 8 x + y - 10 for x = and y = 50

Find the distance using the formula d = r t Given a rate of 75 mph and a time of 1. 5 hours. 1. ) Rewrite the expression : d = r t 2. ) Substitute the values for the variables: d = (75) (1. 5) 3. ) Simplify the expression: d = 112. 5 miles

31 Find the distance traveled if the trip took 3 hrs at a rate of 60 mph.

32 Find the distance traveled if the trip took 1 hr at a rate of 45 mph.

33 Find the distance traveled if the trip took 1/2 hr at a rate of 50 mph.

34 Find the distance traveled if the trip took 5 hr at a rate of 50. 5 mph.

35 Find the distance traveled if the trip took 3. 5 hr at a rate of 50 mph.

The Distributive Property Return to Table of Contents

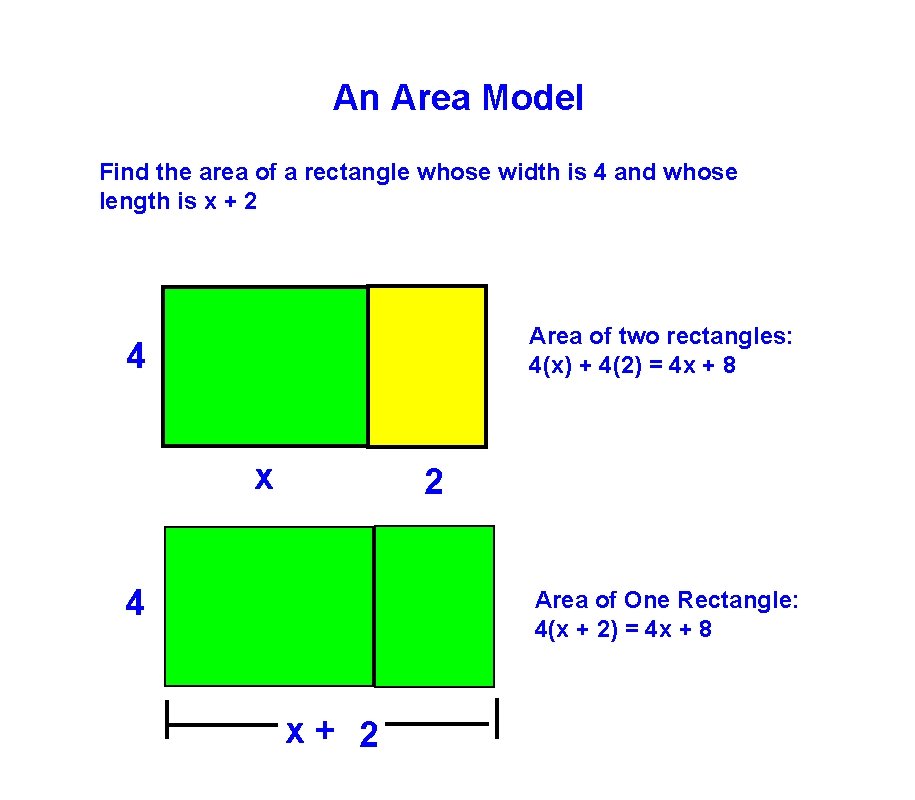
An Area Model Find the area of a rectangle whose width is 4 and whose length is x + 2 Area of two rectangles: 4(x) + 4(2) = 4 x + 8 4 x 2 4 Area of One Rectangle: 4(x + 2) = 4 x + 8 x+ 2

The Distributive Property Finding the area of the rectangles demonstrates the distributive property 4(x + 2) = 4(x) + 4(2) = 4 x + 8 The 4 is distributed to each term of the sum (x + 2) Write an expression equivalent to: 5(x + 3) = 5(x) + 5(3) = 5 x + 15 6(x + 4) = 5(x + 7) = 2(x - 1) = 4(x - 8) =

The Distributive Property a(b + c) = ab + ac Example: 2(x + 3) = 2 x + 6 (b + c)a = ba + ca Example: (x + 7)3 = 3 x + 21 a(b - c) = ab - ac Example: 5(x - 2) = 5 x - 10 (b - c)a = ba - ca Example: (x - 3)6 click = 6 xto- reveal 18

The Distributive Property is often used to eliminate the parentheses in expressions like 4(x + 2). This makes it possible to combine like terms in more complicated expressions. EXAMPLE: 3(4 x - 6) = 3(4 x) - 3(6) = 12 x - 18 -2(x + 3) = -2(x) + -2(3) = -2 x + -6 or -2 x - 6 -3(4 x - 6) = -3(4 x) - -3(6) = -12 x - -18 or -12 x + 18 TRY THESE: 4(7 x + 5) = -6(2 x + 4) = -3(5 m - 8) =

Keep in mind that when there is a negative sign out side of the parenthesis it really is a -1. For example: -(3 x + 4) = -1(3 x) + -1(4) = -3 x - 4 What do you notice about the original problem and its answer? Remove to see answer. The numbers are turned to their opposites. Try these: -(2 x + 5) = -(-5 x + 3) = -(6 x - 7) = -(-x - 9) =

36 4(x + 6) = 4 + 4(6) True False

37 Use the distributive property to rewrite the expression without parentheses 2(x + 5) A 2 x + 5 B 2 x + 10 C x + 10 D 7 x

38 Use the distributive property to rewrite the expression without parentheses (x - 6)3 A 3 x - 6 B 3 x - 18 C x - 18 D 15 x

39 Use the distributive property to rewrite the expression without parentheses -4 (x - 9) A -4 x - 36 B 4 x - 36 C -4 x + 36 D 32 x

40 Use the distributive property to rewrite the expression without parentheses - (4 x - 2) A -4 x - 2 C -4 x + 2 B D 4 x + 2

Combining Like Terms Return to Table of Contents

Like terms: terms in an expression that have the same variable raised to the same power Like Terms NOT Like Terms 6 x and x 6 x and 2 x 5 y and 8 y 2 2 4 x and 7 x 2 2 4 x and x 4

41 Identify all of the terms like 5 y A 5 B 4 y 2 C 18 y D 18 y E -1 y

42 Identify all of the terms like 8 x A 5 x B 4 x 2 C 8 y D 8 E -10 x

43 Identify all of the terms like 8 xy A 5 x 2 B 4 x y C 3 xy D 8 y E -10 xy

44 Identify all of the terms like 2 y A 51 y B 2 w C 3 y D 2 x E -10 y

45 Identify all of the terms like 14 x A 5 x B 2 x C 3 y 2 2 D 2 x E -10 x 2 2

Simplify by combining like terms 6 x + 3 x = (6 + 3)x = 9 x 5 x + 2 x = (5 + 2)x = 7 x 4 + 5(x + 3) = 4 + 5(x) + 5(3) = 4 + 5 x + 15 = 5 x + 19 7 y - 4 y = (7 - 4)y = 3 y Notice that when combining like terms, you add/subtract the coefficients but the variable remains the same.

Try These: 8 x + 9 x 7 y - 5 y 6 + 2 x + 12 x 7 y + 7 x

46 8 x + 3 x = 11 x True False

47 7 x + 7 y = 14 xy True False

48 4 x + 4 x = 8 x True False 2

49 -12 y + 4 y = -8 y True False

50 -3 + y + 5 = 2 y True False

51 -3 y + 5 y = 2 y True False

52 7 x -3(x - 4) = 4 x +12 True False

53 7 +(x + 2)5 = 5 x + 9 True False

54 4 +(x - 3)6 = 6 x -14 True False

55 3 x + 2 y + 4 x + 12 = 9 xy + 12 True False

56 2 2 2 3 x + 7 x + 5(x + 3) + x = 4 x + 12 x + 15 True False

57 3 2 2 3 2 9 x + 2 x + 3(x + x) + 5 x = 9 x + 5 x + 6 x True False

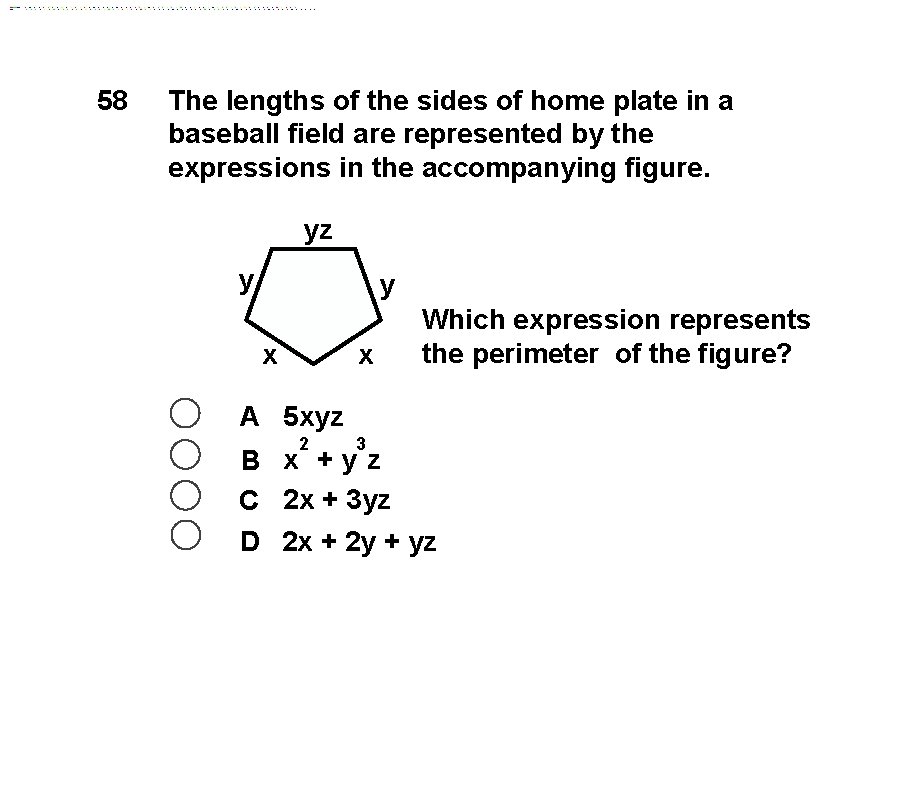
58 The lengths of the sides of home plate in a baseball field are represented by the expressions in the accompanying figure. yz y y x x Which expression represents the perimeter of the figure? A 5 xyz 2 3 B x +y z C 2 x + 3 yz D 2 x + 2 y + yz

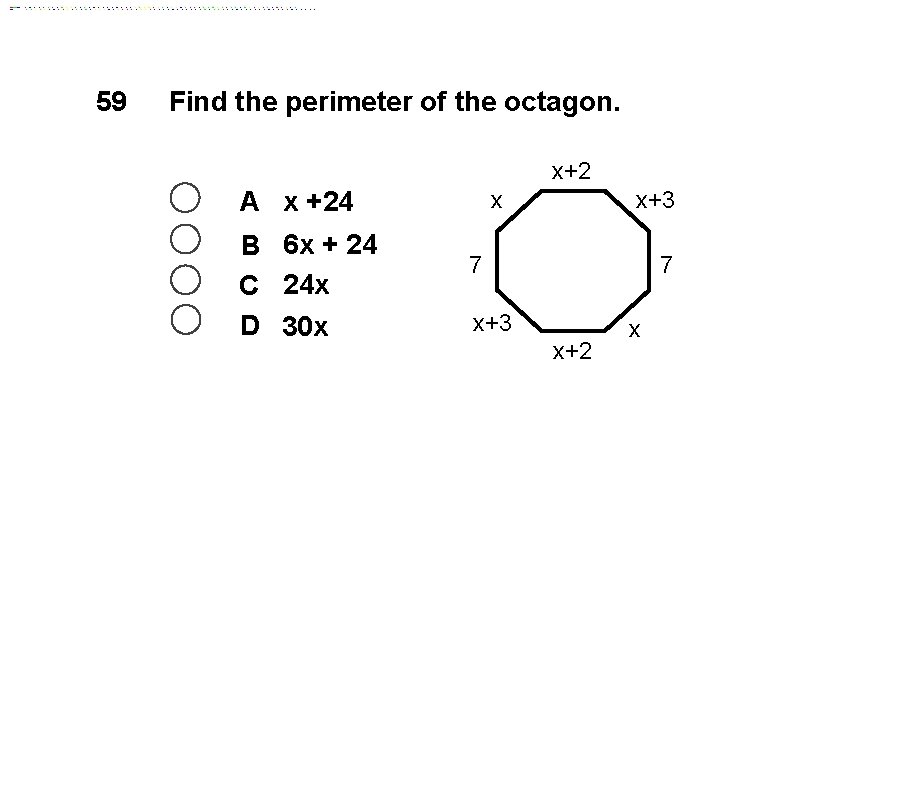
59 Find the perimeter of the octagon. x+2 A x +24 B 6 x + 24 C 24 x D 30 x x x+3 7 7 x+3 x+2 x