Contents of Table A Recurrence solution methods The

Contents of Table A. Recurrence solution methods The substitution method The recursion-tree method The master theorem method 1

2. Recurrence solution methods • Recursion-tree - Definition For come up with good guess, convert the recurrence into a tree that each node represents the cost of a single subproblem somewhere in the set of recursive function invocations. We sum all the per-level costs to determine the total cost of all levels of the recursion 2

2. Recurrence solution methods • Recursion-tree Example The recurrence is T (n) = 3 T (�n/4�) + Θ(n 2) = 3 T (n/4) + cn 2 Use the recursion tree to making a good guess for upper bound for the solution. 3

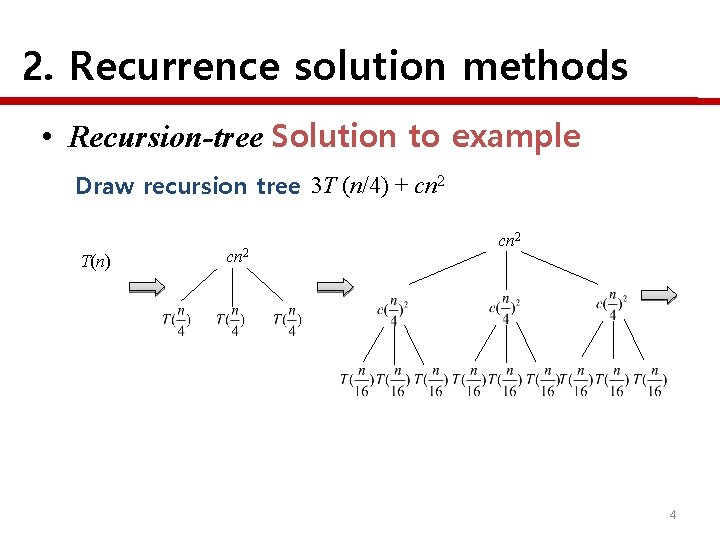
2. Recurrence solution methods • Recursion-tree Solution to example Draw recursion tree 3 T (n/4) + cn 2 T(n) cn 2 4

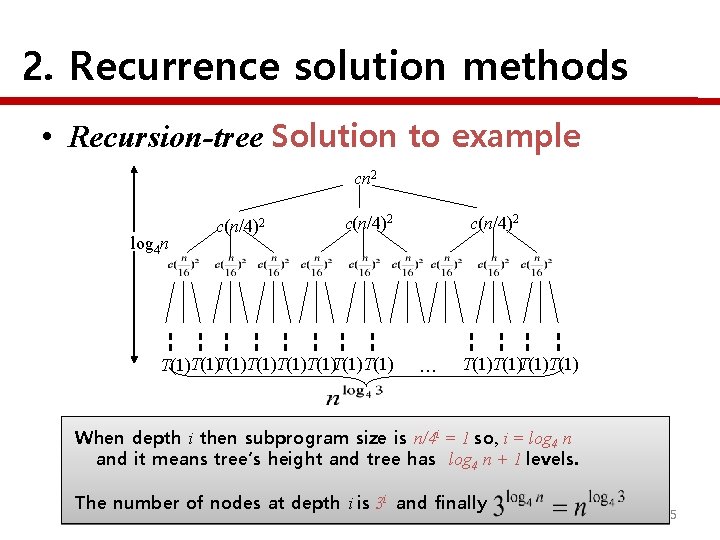
2. Recurrence solution methods • Recursion-tree Solution to example cn 2 log 4 n c(n/4)2 T(1)T(1)T(1)T(1) c(n/4)2 … T(1)T(1) When depth i then subprogram size is n/4 i = 1 so, i = log 4 n and it means tree’s height and tree has log 4 n + 1 levels. The number of nodes at depth i is 3 i and finally 5

2. Recurrence solution methods • Recursion-tree Solution to example Total Cost Sum of cost for i depth Sum of cost for root to i-1 depth 6

2. Recurrence solution methods • Recursion-tree Solution to example Total Cost is… ) ( When 0<x<1 then, Now we guess the solution is T (n) = O(n 2) 7

2. Recurrence solution methods • Recursion-tree Solution to example Prove T (n) = O(n 2) by the substitution method Recurrence : Guess : Prove : T (n) = 3 T (�n/4�) + Θ(n 2) = 3 T(� n/4�) + cn 2 2 T (n) = O(n ) T (n) ≤ dn 2 (for some d > 0 and for the same c > 0) Substitution k k+1 means → T (�n/4�) ≤ d (�n/4�) 2 n 8

2. Recurrence solution methods Recursion-tree Solution to example Find constant d T(n) = ≤ ≤ = 3 T(�n/4�) + cn 2 3 d(�n/4�)2 + cn 2 3 d(n/4)2 + cn 2 3/16 dn 2 + cn 2 ≤ dn 2 (where the last step holds as long as d ≥ (16/13)c ) Now we proved the solution is T (n) = O(n 2) 9

2. Recurrence solution methods • Recursion-tree Example The recurrence T (n) = T (n/3)+T(2 n/3)+O(n) Use the recursion tree to making a good guess for upper bound for the solution. 10

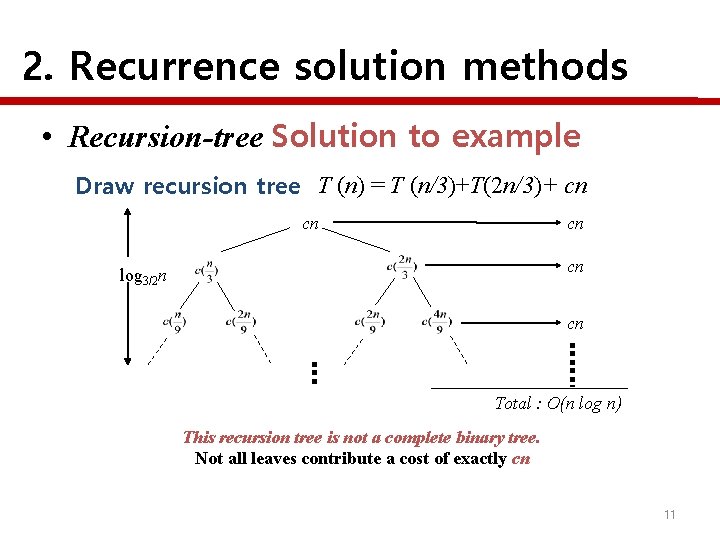
2. Recurrence solution methods • Recursion-tree Solution to example Draw recursion tree T (n) = T (n/3)+T(2 n/3)+ cn cn log 3/2 n cn Total : O(n log n) This recursion tree is not a complete binary tree. Not all leaves contribute a cost of exactly cn 11

2. Recurrence solution methods • Recursion-tree Solution to example Draw recursion tree T (n) = T (n/3)+T(2 n/3)+ cn cn log 3/2 n cn cn cn The longest path from root to a leaf is n→(2/3)n → (2/3)2 n → … → 1. Since, (2/3)kn = 1 when k=log 3/2 n and it means tree’s height is log 3/2 n. The total cost = Cost of each level x Height = cn x log 3/2 n = O(cnlog 3/2 n) = O(n lg n) 12

2. Recurrence solution methods • Recursion-tree Solution to example Prove T (n) = O(n lg n) by the substitution method Recurrence : Guess : Prove : T(n/3) + T(2 n/3) + cn T (n) = O(n lg n) T (n) ≤ d n lg n (for some d > 0 and for the same c > 0) Substitution k means → → k+1 means n 13

2. Recurrence solution methods Recursion-tree Solution to example Find constant d T(n) = T(n/3) + T(2 n/3) + cn ≤ d(n/3)lg(n/3) + d(2 n/3)lg(2 n/3) + cn = (d(n/3)lgn - d(n/3)lg 3) + (d(2 n/3)lgn – d(2 n/3)lg(3/2)) + cn = dnlgn - d((n/3)lg 3 + (2 n/3)lg 3 - (2 n/3)lg 2) + cn = dnlgn - dn(lg 3 - 2/3) + cn ≤ dnlgn (as long as d ≥ c/(lg 3 - (2/3)) ) Now we proved the solution is T (n) = O(n log n ) 14