Contents Introduction Design Procedure of LRB Numerical Examples

Contents Introduction Design Procedure of LRB Numerical Examples Conclusions Structural Dynamics & Vibration Control Lab. , KAIST 2

Introduction Backgrounds Lead Rubber Bearing (LRB) Design procedure of base isolation system for building and short-span bridges. - Design natural period of structure or effective period of base isolator - Then, the design parameters of isolator are determined. Structural Dynamics & Vibration Control Lab. , KAIST 3

Long span bridge such as cable-stayed bridges - Flexible : long period modes and natural seismic isolation - Small structural damping it is difficult to apply this procedure and guidelines of isolation system directly to cable-stayed bridges. Structural Dynamics & Vibration Control Lab. , KAIST 4

Objective Suggest the design procedure and guidelines of LRB for cable-stayed bridge. Structural Dynamics & Vibration Control Lab. , KAIST 5

Design Procedure of LRB Design Parameters of LRB , : elastic & plastic stiffness : effective stiffness : characteristic shear strength , : yield and ultimate displacement Fig. 1 Behavior and design parameters of LRB Flexibility of rubber : period shift Plastic behavior of lead : energy dissipation Determine the , , to minimize the earthquake forces and displacements. Structural Dynamics & Vibration Control Lab. , KAIST 6

Proposed Design Procedure The design parameters of LRB are chosen that design index (DI) is minimized or unchanged (less than 0. 05) for variation of design parameters. i=1~5 - Five important responses of cable-stayed bridge are considered. : base shear and moment at towers : shear and moment at deck level at towers : deck displacement (longitudinal direction) Structural Dynamics & Vibration Control Lab. , KAIST 7

Design procedure - Step 1 : design earthquake (history or artificial earthquake, etc. ) - Step 2 : appropriate is selected for variation of. : and are assumed. - Step 3 : appropriate is selected for variation of. : use selected and assume. - Step 4 : appropriate is selected for variation of . - Step 5 : iterate step 2 ~ 4 until parameters remain unchanged. Structural Dynamics & Vibration Control Lab. , KAIST 8

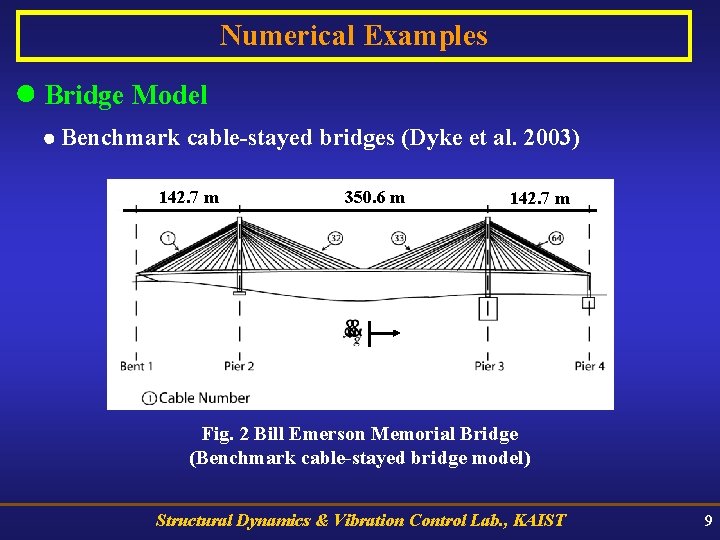
Numerical Examples Bridge Model Benchmark cable-stayed bridges (Dyke et al. 2003) 142. 7 m 350. 6 m 142. 7 m Fig. 2 Bill Emerson Memorial Bridge (Benchmark cable-stayed bridge model) Structural Dynamics & Vibration Control Lab. , KAIST 9

Finite element evaluation model - Modeling : 162 beam elements, 420 rigid links 128 cable elements, 579 nodes - Stiffness matrix : nonlinear static analysis corresponding to the deformed stated of bridge with dead loads - Damping matrix : 3 % of critical damping to each mode - Control devices : longitudinal direction between the deck and piers - Ground motion : longitudinal direction not considering multi-excitation Structural Dynamics & Vibration Control Lab. , KAIST 10

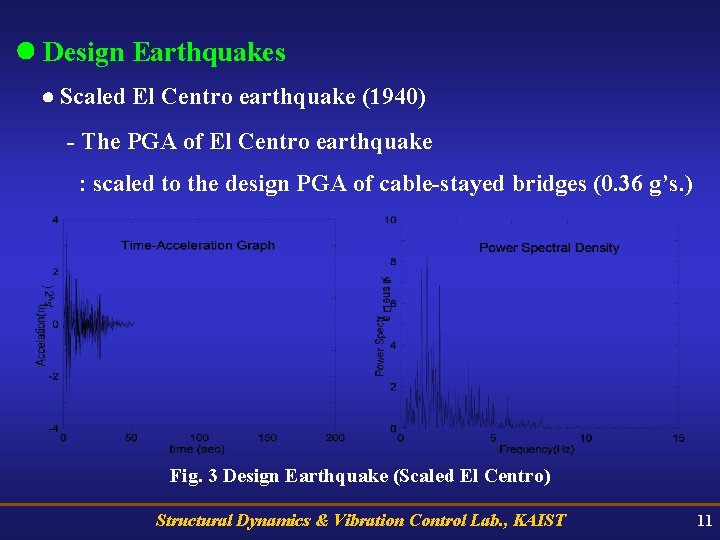
Design Earthquakes Scaled El Centro earthquake (1940) - The PGA of El Centro earthquake : scaled to the design PGA of cable-stayed bridges (0. 36 g’s. ) Fig. 3 Design Earthquake (Scaled El Centro) Structural Dynamics & Vibration Control Lab. , KAIST 11

Kanai-Tajimi artificial earthquake - Stationary Kanai-Tajimi filter - Power spectral density and : site dominant damping coefficient and frequency. : constant power spectral intensity. - = 37. 3 rad/s, = 0. 3 (Spencer et al. ) Structural Dynamics & Vibration Control Lab. , KAIST 12

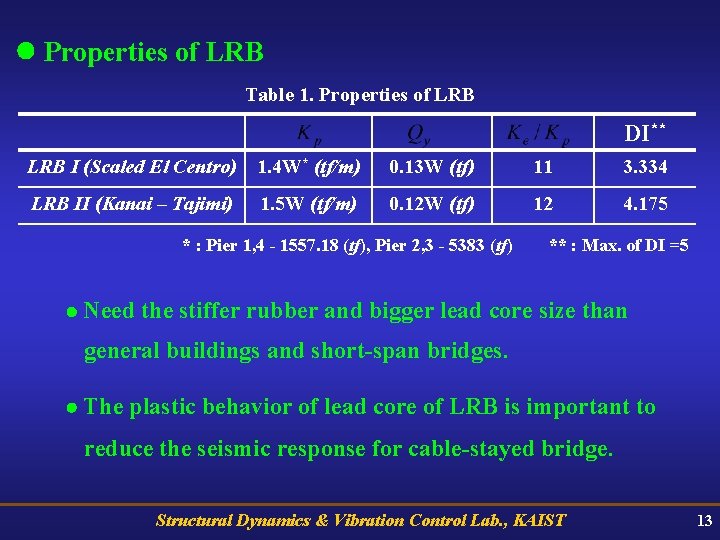
Properties of LRB Table 1. Properties of LRB DI** LRB I (Scaled El Centro) 1. 4 W* (tf/m) 0. 13 W (tf) 11 3. 334 LRB II (Kanai – Tajimi) 1. 5 W (tf/m) 0. 12 W (tf) 12 4. 175 * : Pier 1, 4 - 1557. 18 (tf), Pier 2, 3 - 5383 (tf) ** : Max. of DI =5 Need the stiffer rubber and bigger lead core size than general buildings and short-span bridges. The plastic behavior of lead core of LRB is important to reduce the seismic response for cable-stayed bridge. Structural Dynamics & Vibration Control Lab. , KAIST 13

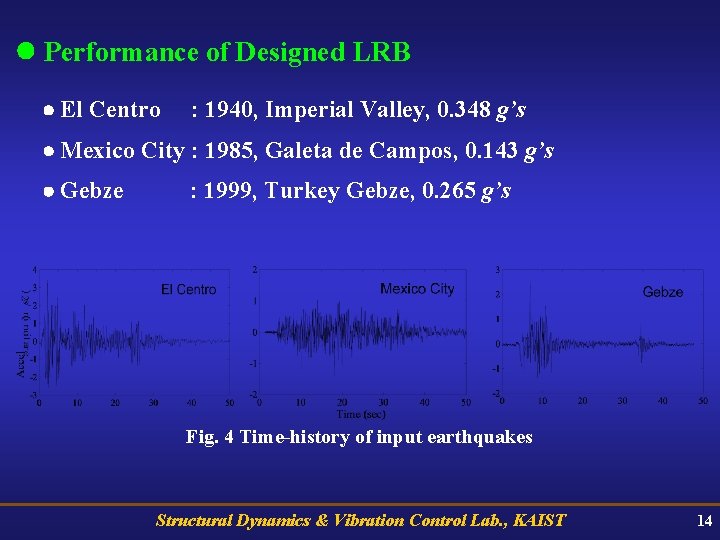
Performance of Designed LRB El Centro : 1940, Imperial Valley, 0. 348 g’s Mexico City : 1985, Galeta de Campos, 0. 143 g’s Gebze : 1999, Turkey Gebze, 0. 265 g’s Fig. 4 Time-history of input earthquakes Structural Dynamics & Vibration Control Lab. , KAIST 14

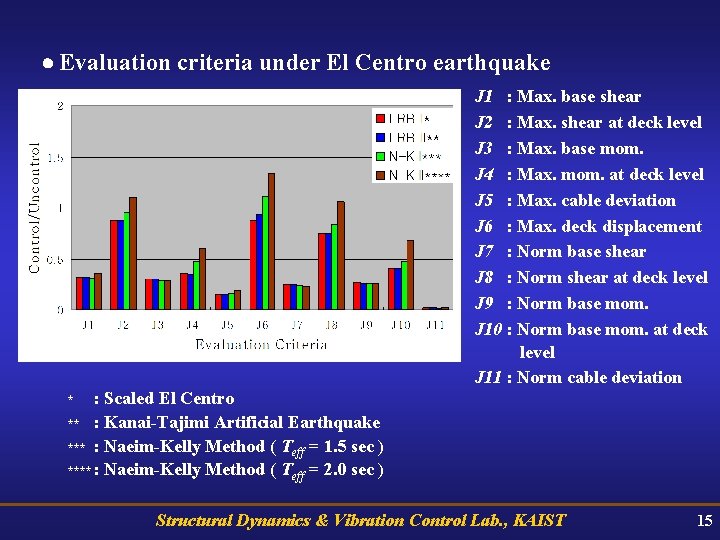
Evaluation criteria under El Centro earthquake J 1 : Max. base shear J 2 : Max. shear at deck level J 3 : Max. base mom. J 4 : Max. mom. at deck level J 5 : Max. cable deviation J 6 : Max. deck displacement J 7 : Norm base shear J 8 : Norm shear at deck level J 9 : Norm base mom. J 10 : Norm base mom. at deck level J 11 : Norm cable deviation : Scaled El Centro ** : Kanai-Tajimi Artificial Earthquake *** : Naeim-Kelly Method ( Teff = 1. 5 sec ) **** : Naeim-Kelly Method ( Teff = 2. 0 sec ) * Structural Dynamics & Vibration Control Lab. , KAIST 15

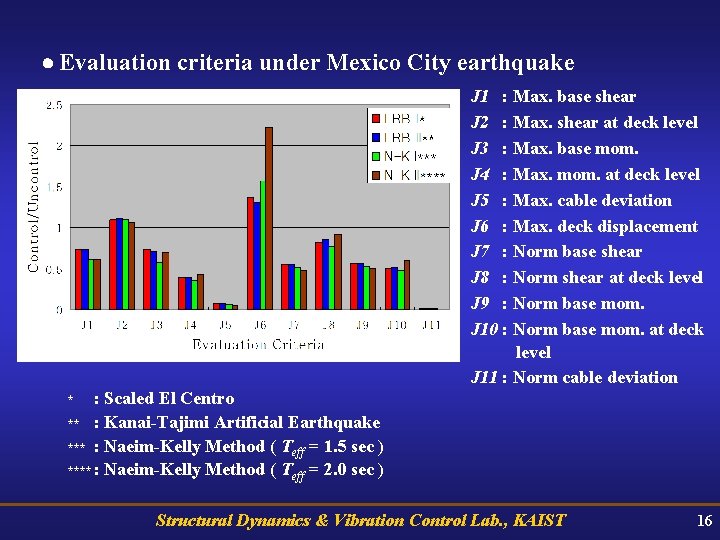
Evaluation criteria under Mexico City earthquake J 1 : Max. base shear J 2 : Max. shear at deck level J 3 : Max. base mom. J 4 : Max. mom. at deck level J 5 : Max. cable deviation J 6 : Max. deck displacement J 7 : Norm base shear J 8 : Norm shear at deck level J 9 : Norm base mom. J 10 : Norm base mom. at deck level J 11 : Norm cable deviation : Scaled El Centro ** : Kanai-Tajimi Artificial Earthquake *** : Naeim-Kelly Method ( Teff = 1. 5 sec ) **** : Naeim-Kelly Method ( Teff = 2. 0 sec ) * Structural Dynamics & Vibration Control Lab. , KAIST 16

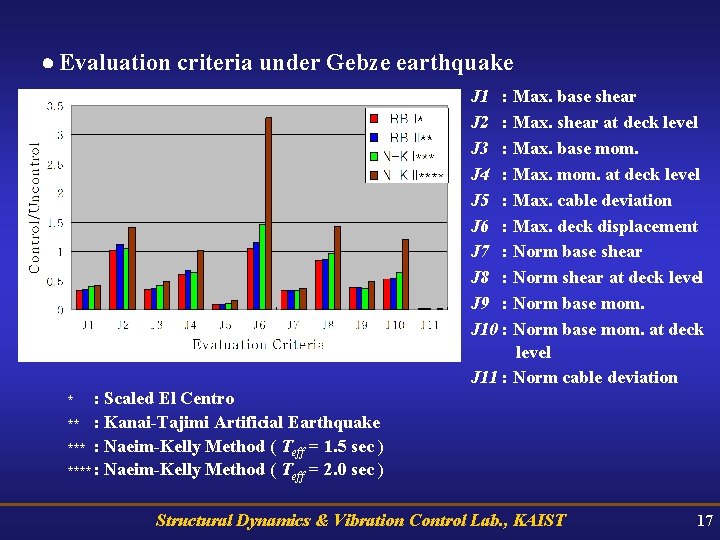
Evaluation criteria under Gebze earthquake J 1 : Max. base shear J 2 : Max. shear at deck level J 3 : Max. base mom. J 4 : Max. mom. at deck level J 5 : Max. cable deviation J 6 : Max. deck displacement J 7 : Norm base shear J 8 : Norm shear at deck level J 9 : Norm base mom. J 10 : Norm base mom. at deck level J 11 : Norm cable deviation : Scaled El Centro ** : Kanai-Tajimi Artificial Earthquake *** : Naeim-Kelly Method ( Teff = 1. 5 sec ) **** : Naeim-Kelly Method ( Teff = 2. 0 sec ) * Structural Dynamics & Vibration Control Lab. , KAIST 17

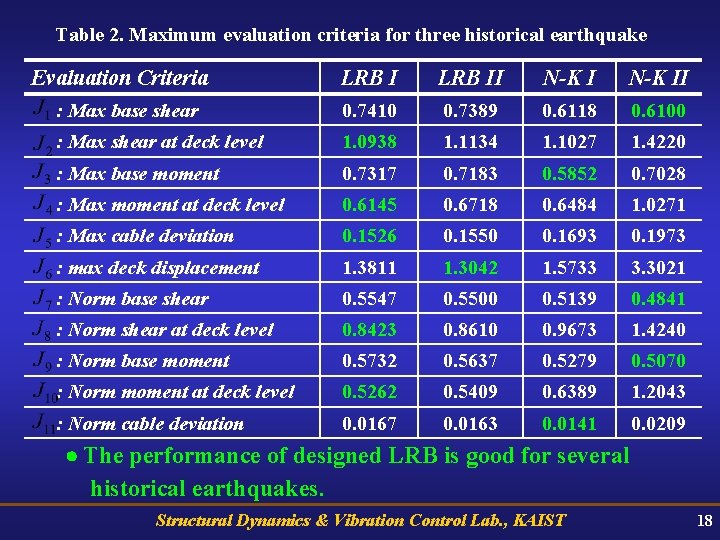
Table 2. Maximum evaluation criteria for three historical earthquake Evaluation Criteria LRB II N-K II : Max base shear 0. 7410 0. 7389 0. 6118 0. 6100 : Max shear at deck level 1. 0938 1. 1134 1. 1027 1. 4220 : Max base moment 0. 7317 0. 7183 0. 5852 0. 7028 : Max moment at deck level 0. 6145 0. 6718 0. 6484 1. 0271 : Max cable deviation 0. 1526 0. 1550 0. 1693 0. 1973 : max deck displacement 1. 3811 1. 3042 1. 5733 3. 3021 : Norm base shear 0. 5547 0. 5500 0. 5139 0. 4841 : Norm shear at deck level 0. 8423 0. 8610 0. 9673 1. 4240 : Norm base moment 0. 5732 0. 5637 0. 5279 0. 5070 : Norm moment at deck level 0. 5262 0. 5409 0. 6389 1. 2043 : Norm cable deviation 0. 0167 0. 0163 0. 0141 0. 0209 The performance of designed LRB is good for several historical earthquakes. Structural Dynamics & Vibration Control Lab. , KAIST 18

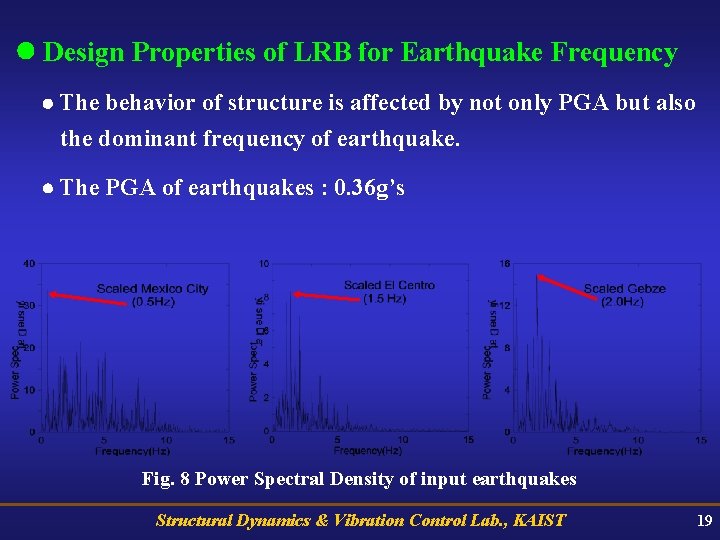
Design Properties of LRB for Earthquake Frequency The behavior of structure is affected by not only PGA but also the dominant frequency of earthquake. The PGA of earthquakes : 0. 36 g’s Fig. 8 Power Spectral Density of input earthquakes Structural Dynamics & Vibration Control Lab. , KAIST 19

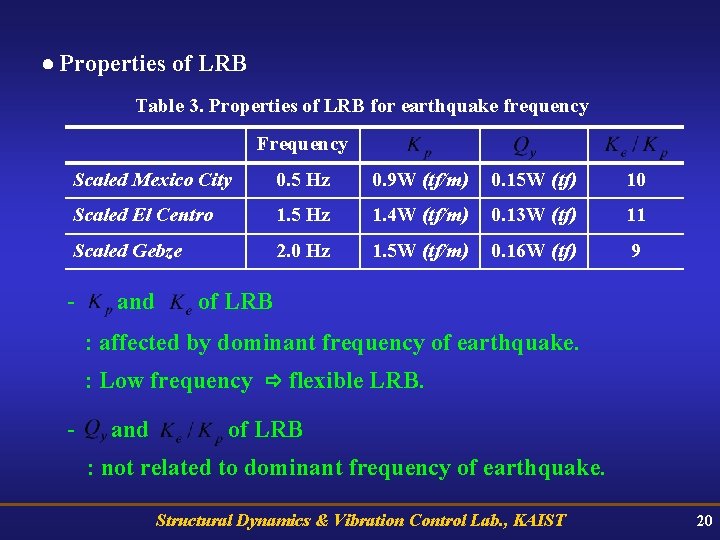
Properties of LRB Table 3. Properties of LRB for earthquake frequency Frequency Scaled Mexico City 0. 5 Hz 0. 9 W (tf/m) 0. 15 W (tf) 10 Scaled El Centro 1. 5 Hz 1. 4 W (tf/m) 0. 13 W (tf) 11 Scaled Gebze 2. 0 Hz 1. 5 W (tf/m) 0. 16 W (tf) 9 - and of LRB : affected by dominant frequency of earthquake. : Low frequency flexible LRB. - and of LRB : not related to dominant frequency of earthquake. Structural Dynamics & Vibration Control Lab. , KAIST 20

Conclusions The guidelines and procedure of designing LRB for seismically excited cable-stayed bridge are investigated. The cable-stayed bridge is needed stiffer rubber and bigger lead core size than general structures. The plastic behavior of lead core of LRB is important to reduce the seismic response of cable-stayed bridge. Structural Dynamics & Vibration Control Lab. , KAIST 21

The performance of designed LRB is good for several historical earthquakes. As the dominant frequency of earthquake is low, the flexible LRB is needed. Structural Dynamics & Vibration Control Lab. , KAIST 22

Acknowledgments This research is supported by the National Research Lab. Grant (No. : 2000 -N-NL-01 -C-251) in Korea. Thank you for your attention!! Structural Dynamics & Vibration Control Lab. , KAIST 23

Structural Dynamics & Vibration Control Lab. , KAIST 24

Previous Application of LRB for cable-stayed bridge Ali and Abdel-Ghaffar - Efficiency of LRB for cable-stayed bridge Wesolowsky and Wilson - Design the LRB for cable-stayed bridge using N-K method. - Effective period of LRB Structural Dynamics & Vibration Control Lab. , KAIST 25

Design Procedure of LRB for General Structures The natural period of general building and continuous bridge is 0. 3 sec ~ 0. 6 sec. The main design aim for these structures is shifting the natural period of these structures. The stiffness of LRB is designed that the natural period of structure or effective period of isolator is 1. 4 sec ~ 2. 0 sec. The characteristic strength of LRB is recommended to use five percent of weight carried by LRB to obtain additional damping effect. (Ghobarah, A. and Ali, H. M. , 1988) Structural Dynamics & Vibration Control Lab. , KAIST 26

Design Procedure (N-K Method) 1. Maximum allowable displacement( ) and shear-force( ) of isolator is established. 2. Effective stiffness and period of isolator is calculated. where, M is the structural mass assigned to the isolator 3. The effective damping ( ). 4. Energy dissipation of isolator per one cycle. Structural Dynamics & Vibration Control Lab. , KAIST 27

5. Shear strength ( ) - In the first step, is neglecting. 6. Post-yield stiffness ( ) 7. Yield displacement ( ) 8. Repeat 6~8 until converges. Structural Dynamics & Vibration Control Lab. , KAIST 28

LRB Model (Bouc-Wen Model) where : Post to pre-yielding stiffness ratio of LRB : Linear stiffness of LRB : Yielding displacement of lead : Relative displacement & velocity : Dimensionless parameter to represent shape of hysteretic curve = 1, = 0. 5, = 0. 5 Structural Dynamics & Vibration Control Lab. , KAIST 29

Evaluation Criteria Five important responses of cable-stayed bridge are considered. Table 1 Evaluation criteria (Control/Uncontrolled) Scaled El Centro Kanai - Tajimi J 1 Max. base shear at tower RMS J 1 RMS base shear at tower J 2 Max. base moment at tower RMS J 2 RMS base moment at tower J 3 Max. shear at deck level RMS J 3 RMS shear at deck level J 4 Max. moment at deck level RMS J 4 RMS moment at deck level J 6 Max. deck displacement RMS J 6 RMS deck displacement Structural Dynamics & Vibration Control Lab. , KAIST 30

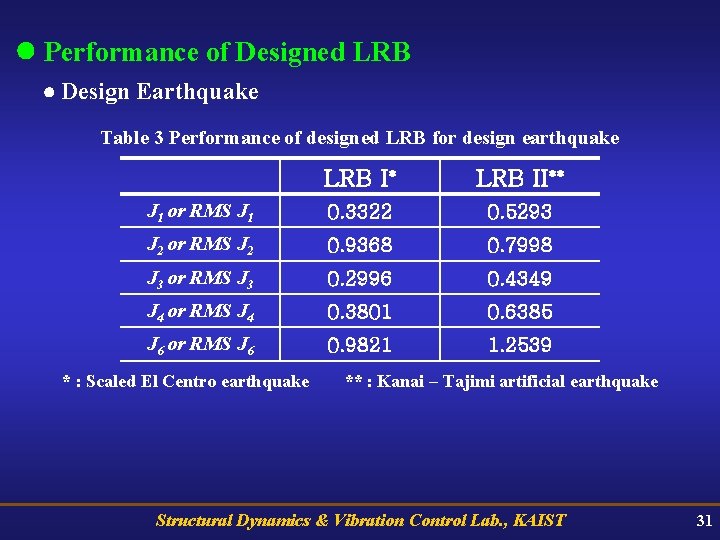
Performance of Designed LRB Design Earthquake Table 3 Performance of designed LRB for design earthquake LRB I* LRB II** J 1 or RMS J 1 0. 3322 0. 5293 J 2 or RMS J 2 0. 9368 0. 7998 J 3 or RMS J 3 0. 2996 0. 4349 J 4 or RMS J 4 0. 3801 0. 6385 J 6 or RMS J 6 0. 9821 1. 2539 * : Scaled El Centro earthquake ** : Kanai – Tajimi artificial earthquake Structural Dynamics & Vibration Control Lab. , KAIST 31

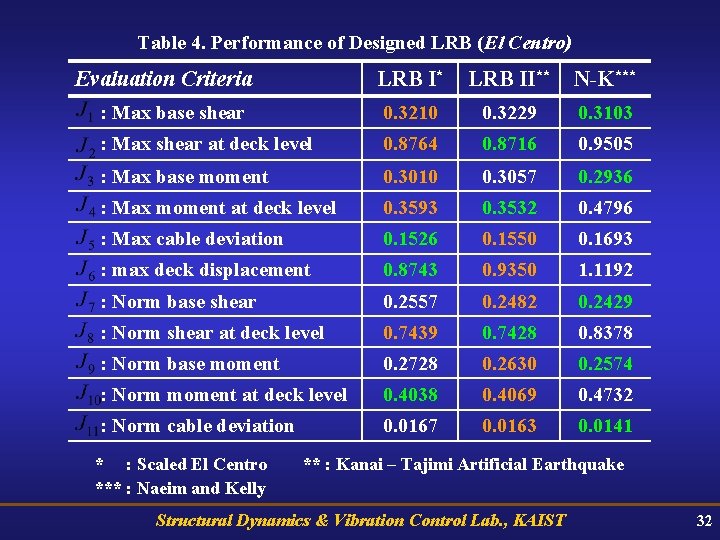
Table 4. Performance of Designed LRB (El Centro) Evaluation Criteria LRB I* LRB II** N-K*** : Max base shear 0. 3210 0. 3229 0. 3103 : Max shear at deck level 0. 8764 0. 8716 0. 9505 : Max base moment 0. 3010 0. 3057 0. 2936 : Max moment at deck level 0. 3593 0. 3532 0. 4796 : Max cable deviation 0. 1526 0. 1550 0. 1693 : max deck displacement 0. 8743 0. 9350 1. 1192 : Norm base shear 0. 2557 0. 2482 0. 2429 : Norm shear at deck level 0. 7439 0. 7428 0. 8378 : Norm base moment 0. 2728 0. 2630 0. 2574 : Norm moment at deck level 0. 4038 0. 4069 0. 4732 : Norm cable deviation 0. 0167 0. 0163 0. 0141 * : Scaled El Centro *** : Naeim and Kelly ** : Kanai – Tajimi Artificial Earthquake Structural Dynamics & Vibration Control Lab. , KAIST 32

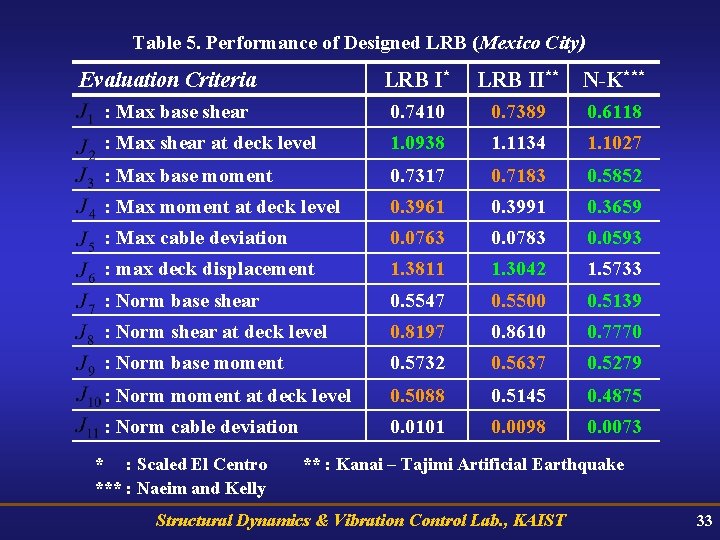
Table 5. Performance of Designed LRB (Mexico City) Evaluation Criteria LRB I* LRB II** N-K*** : Max base shear 0. 7410 0. 7389 0. 6118 : Max shear at deck level 1. 0938 1. 1134 1. 1027 : Max base moment 0. 7317 0. 7183 0. 5852 : Max moment at deck level 0. 3961 0. 3991 0. 3659 : Max cable deviation 0. 0763 0. 0783 0. 0593 : max deck displacement 1. 3811 1. 3042 1. 5733 : Norm base shear 0. 5547 0. 5500 0. 5139 : Norm shear at deck level 0. 8197 0. 8610 0. 7770 : Norm base moment 0. 5732 0. 5637 0. 5279 : Norm moment at deck level 0. 5088 0. 5145 0. 4875 : Norm cable deviation 0. 0101 0. 0098 0. 0073 * : Scaled El Centro *** : Naeim and Kelly ** : Kanai – Tajimi Artificial Earthquake Structural Dynamics & Vibration Control Lab. , KAIST 33

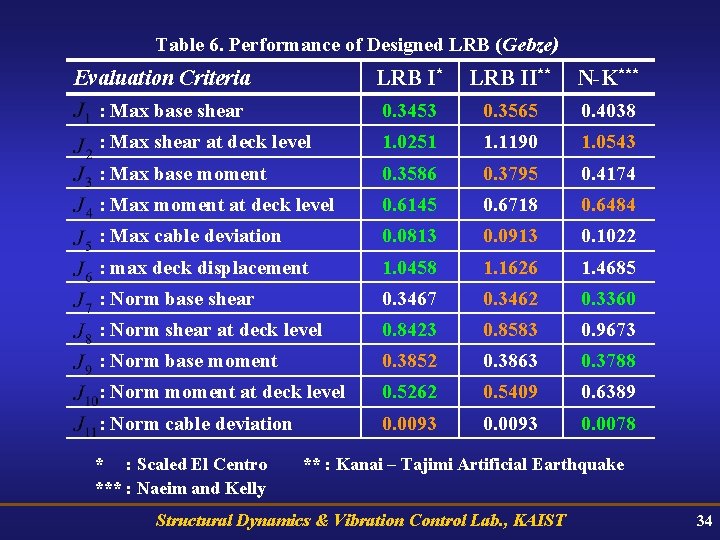
Table 6. Performance of Designed LRB (Gebze) Evaluation Criteria LRB I* LRB II** N-K*** : Max base shear 0. 3453 0. 3565 0. 4038 : Max shear at deck level 1. 0251 1. 1190 1. 0543 : Max base moment 0. 3586 0. 3795 0. 4174 : Max moment at deck level 0. 6145 0. 6718 0. 6484 : Max cable deviation 0. 0813 0. 0913 0. 1022 : max deck displacement 1. 0458 1. 1626 1. 4685 : Norm base shear 0. 3467 0. 3462 0. 3360 : Norm shear at deck level 0. 8423 0. 8583 0. 9673 : Norm base moment 0. 3852 0. 3863 0. 3788 : Norm moment at deck level 0. 5262 0. 5409 0. 6389 : Norm cable deviation 0. 0093 0. 0078 * : Scaled El Centro *** : Naeim and Kelly ** : Kanai – Tajimi Artificial Earthquake Structural Dynamics & Vibration Control Lab. , KAIST 34