Contents Balanced Incomplete Block Design BIBD Projective Plane

Contents • Balanced Incomplete Block Design (BIBD) & Projective Plane • Generalized Quadrangle (GQ) • Mapping and Construction • Analysis

Balanced Incomplete Block Design (BIBD) • • • There are v distinct object There are b blocks Each block contains exactly k distinct objects Each object occurs in exactly r different blocks Every pair of distinct object occurs together in exactly blocks • Can be expressed as or •

Symmetric BIBD (or Symmetric Design) • A BIBD is called Symmetric BIBD (or Symmetric Design) when b=v and therefore r=k • Symmetric BIBD has 4 properties: – Every block contains k=r objects – Every object occurs in r=k blocks – Every pair of object occurs in blocks – Every pair of blocks intersects on objects

Example • • or • There are b=7 blocks and each one contains k=3 objects • Every objects occurs in r=3 blocks • Every pair of distinct objects occurs in Blocks • Every pair of blocks intersects in objects

’Example Cont • Based on a construction algorithm the blocks are:

Projective Plane • Consist of finite set P of points and a set of subsets of P, called lines • A Projective Plane of order q (q>1) has 4 properties – – Every line contains exactly q+1 points Every point occurs on exactly q+1 lines There are exactly points There are exactly lines

’Projective Plane cont • Theorem: If we consider lines as blocks and points as objects, then Projective Plane of order q is a Symmetric BIBD with parameters: • Theorem: For every prime power q>1 there exist a Symmetric BIBD (Projective Plane of order q)

Complementary Design • Theorem: If is a symmetric BIBD, then is also a symmetric BIBD • Example: Consider Complementary Design of this design is: with the following blocks:

Contents • Balanced Incomplete Block Design (BIBD) & Projective Plane • Generalized Quadrangle (GQ) • Mapping and Construction • Analysis

Projective Space PG(d, q) • Dimension d • Order q • Constructed from the vector space of dimension d+1 over the field finite F – Objects are subspaces of the vector space – Two objects are incident if one contains the other

Projective Space PG(d, q) • Subspace dimensions – Point if dimension 1 – Line if dimension 2 – Hyperplane if dimension d • Order of a projective space is one less than the number of points incident in a line

Partial Linear Space • Arrangement of objects into subsets called lines • Properties – Every line is incident with at least two points – Any two points are incident with at most one line

Incidence Structure • includes – Set of points – Set of lines – Symmetric incidence relation

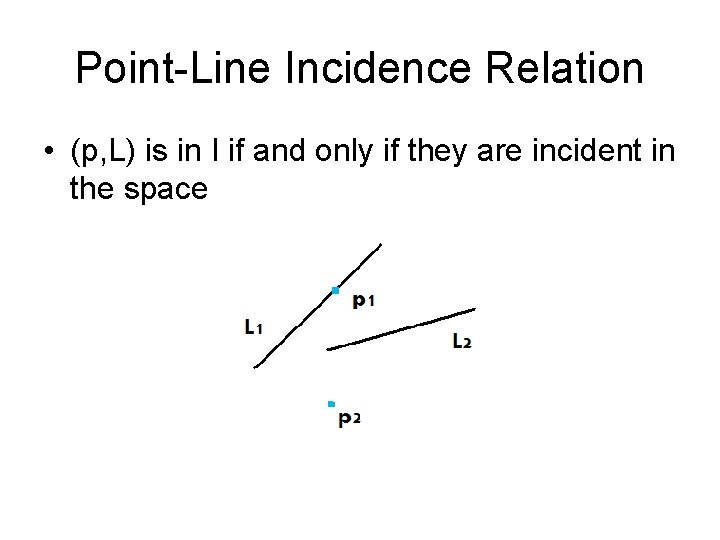
Point-Line Incidence Relation • (p, L) is in I if and only if they are incident in the space

Point-Line Incidence Relation • Axioms – Two distinct points are incident with at most one line. – Two distinct lines are incident with at most one point

Generalized Quadrangle • GQ(s, t) is a subset of a special Partial Linear Space subset called Partial Geometry • Incidence structure S = (P, B, I) – P set of points – B set of lines – I symmetric point-line incidence relation satisfying: • A The above Axioms • B Each point is incident with t+1 lines (t>=1) • C Each line is incident with s+1 points (s>=1)

Generalized Quadrangle I point-line incidence relation satisfying D

GQ(s, t) • v = (s+1)(st+1) points • b = (t+1)(st+1) lines • Each line includes (s+1) points and each point appears in (t+1) lines

3 known GQ’s • GQ(q, q) from PG(4, q) • GQ(q, q²) from PG(5, q) • GQ(q², q³) from PG(4, q²) • In GQ(q, q) – b = v = (q+1)(q²+1)

Example • • GQ(2, 2) for q = 2 v = b = (2+1)(2*2+1) = 15 Each block contains 2+1 objects Each object is contained in 2+1 blocks

Example cont.

Contents • Balanced Incomplete Block Design (BIBD) & Projective Plane • Generalized Quadrangle (GQ) • Mapping and Construction • Analysis

Reminder – A Distributed Sensor Network (DSN) • • There are N sensor nodes Each sensor has a key-chain of k keys Keys are selected from a set P of key-pool 2 sensor nodes need to have q keys in common in their key-chain to secure their communication

Mapping from Symmetric Design to Key Distribution

Construction • There are several ways to construct Symmetric BIBD of the form • We will use complete sets of Mutually Orthogonal and Latin Squares (MOLS) to construct Symmetric BIBD (which can be converted to a projective plane of order q)

Construction

Mapping from GQ to Key Distribution • There are t+1 lines passing through a point • Each line has s+1 points • Therefore, each line shares a point with exactly t(s+1) other lines • Moreover, if 2 lines A, B do not share a point there are s+1 distinct lines which share a point with both.

Mapping from GQ to Key Distribution Cont’ • In terms of Key Distribution that means: – A block shares a key with t(s+1) other blocks – If 2 blocks do not share a key, there are s+1 other blocks sharing a key with both

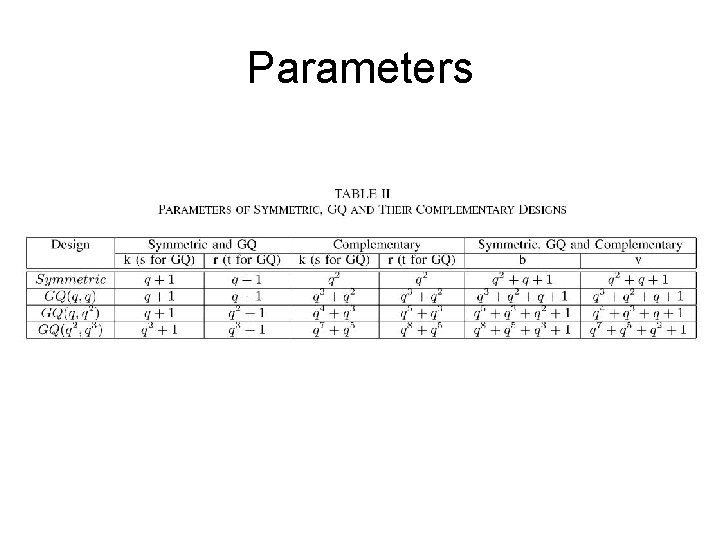
Parameters

Construction

Contents • Balanced Incomplete Block Design (BIBD) & Projective Plane • Generalized Quadrangle (GQ) • Mapping and Construction • Analysis

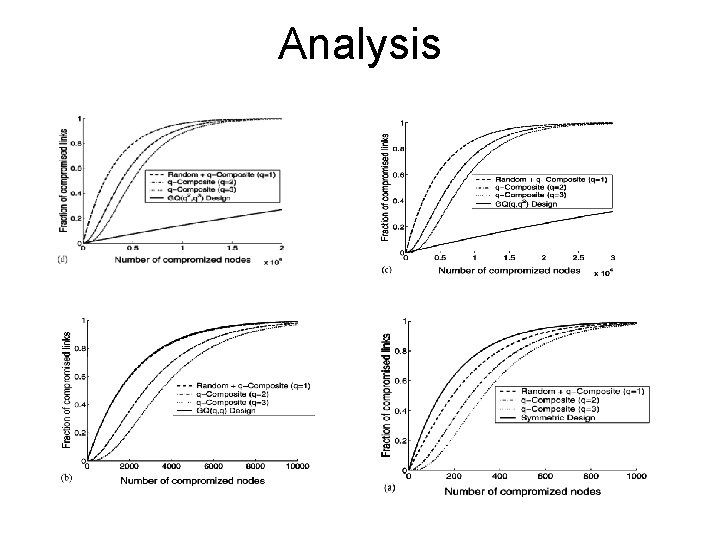
Analysis SD • In a Symmetric Design any pair of blocks share exactly one object • Key share probability between 2 nodes • Average Key-Path Length

Analysis SD • Resilience contradicts with high probability of key sharing • Resilience is compromised • Adversary best case – captures q+1 nodes • Adversary worst case – captures q²+1 nodes

Analysis SD • The probability that a link is compromised when an attacker captures key-chains

Analysis GQ • In a GQ(s, t) there are b = (t+1)(st+1) lines and a line intersects with t(s+1) other lines – Each block shares exactly one object with t(s+1) other blocks – How many blocks does a block share n objects with?

Analysis GQ • Probability two blocks share an object • Adversary worst case – Captures st² + st +1 nodes • Adversary best case – Captures t+1 nodes

Prominent properties • SD highest number of object share • GQ(q, q²) highest number of blocks for fixed block size • GQ(q², q³) smallest block size for fixed number of blocks and has highest resilience

Analysis