Contents A Range B Interquartile range C Standard

Contents • A. Range • B. Interquartile range • C. Standard deviation

A. Range • Range refers to the difference between the maximum value and minimum value of a data set • The larger the range, the more dispersed the data • Calculation steps: Agricultural outputs of Village D's farmers in 2018 Farmer 1 2 3 4 5 6 7 8 9 Agricultural output 12 16 21 15 13 25 24 20 30 (tonnes) Number line showing the dispersion of agricultural outputs of Village D's farmers in 2018 Contents

A. Range ① Find out the maximum value and minimum value in the data set. Maximum value: 30 tonnes Minimum value: 12 tonnes ② Calculate the difference between the maximum value and minimum value. (30 – 12) tonnes = 18 tonnes ∴ The range of agricultural outputs of Village D’s farmers in 2018 is 18 tonnes. Contents

A. Range Merits and demerits of range Merit • Easy to calculate • Easy to explain Contents Demerit • Easily affected by extreme values • Unable to make use of all values in the data set

B. Interquartile range • Sort the data in order and divide it into four equal parts • Then calculate the difference between the upper quartile (Q 3) and lower quartile (Q 1) • The larger the interquartile range (IQR), the more dispersed the data • IQR only considers the dispersion of the 50% of data in the middle, so it is not affected by extreme values IQR = Q 3 – Q 1 Contents

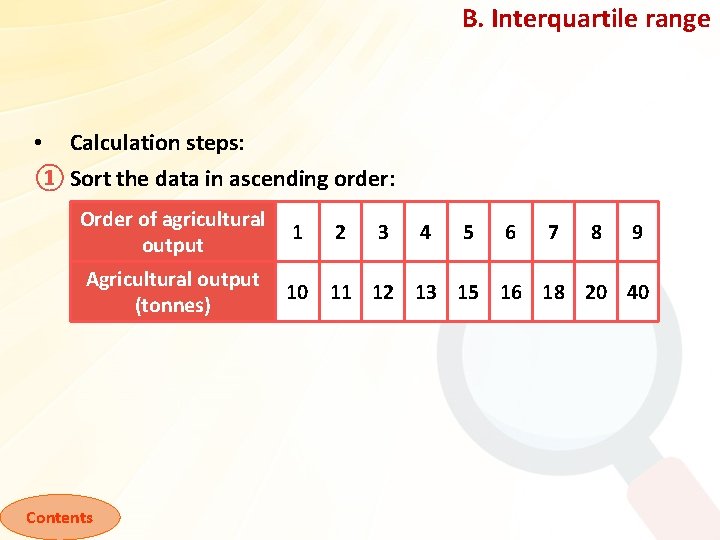
B. Interquartile range • Calculation steps: ① Sort the data in ascending order: Order of agricultural output 1 Agricultural output (tonnes) 10 11 12 13 15 16 18 20 40 Contents 2 3 4 5 6 7 8 9

B. Interquartile range ② Calculate the lower quartile (Q 1) and upper quartile (Q 3). Q 1 = (n + 1) ÷ 4 = (9 + 1) ÷ 4 = 2. 5 Hence, we take the value of the 2. 5 th data point: (11 + 12) tonnes ÷ 2 = 11. 5 tonnes Q 3 = 3[(n + 1) ÷ 4] = 3[(9 + 1) ÷ 4] = 7. 5 Hence, we take the value of the 7. 5 th data point: (18 + 20) tonnes ÷ 2 = 19 tonnes Contents

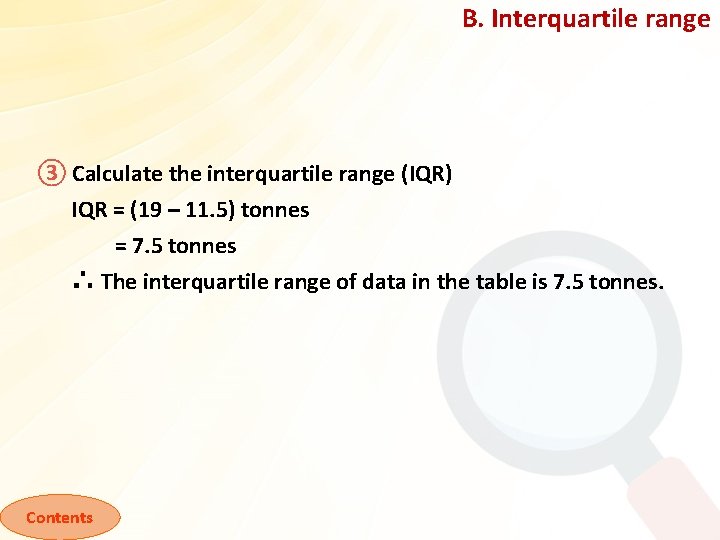
B. Interquartile range ③ Calculate the interquartile range (IQR) IQR = (19 – 11. 5) tonnes = 7. 5 tonnes ∴ The interquartile range of data in the table is 7. 5 tonnes. Contents

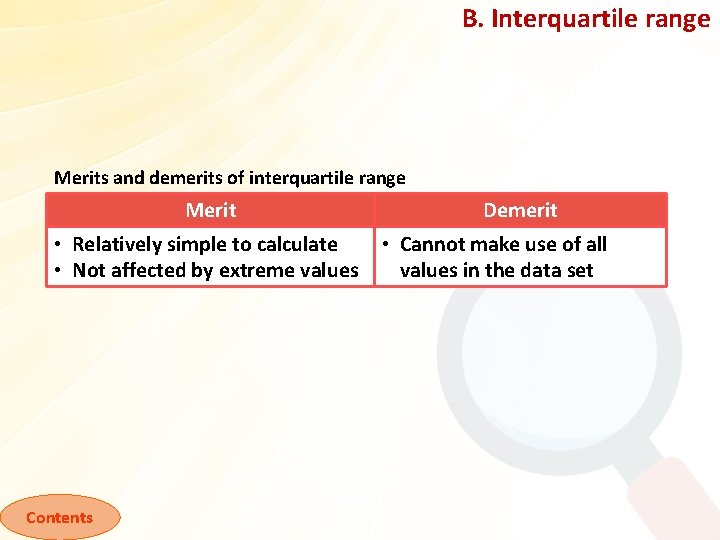
B. Interquartile range Merits and demerits of interquartile range Merit • Relatively simple to calculate • Not affected by extreme values Contents Demerit • Cannot make use of all values in the data set

C. Standard deviation • Contents

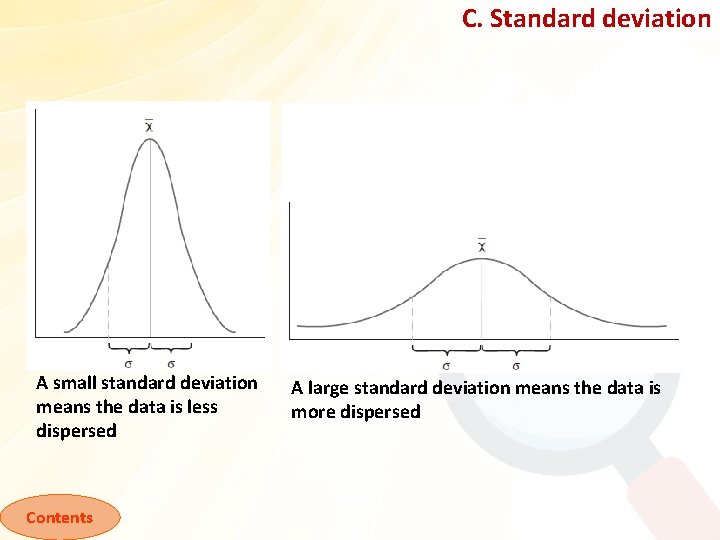
C. Standard deviation A small standard deviation means the data is less dispersed Contents A large standard deviation means the data is more dispersed

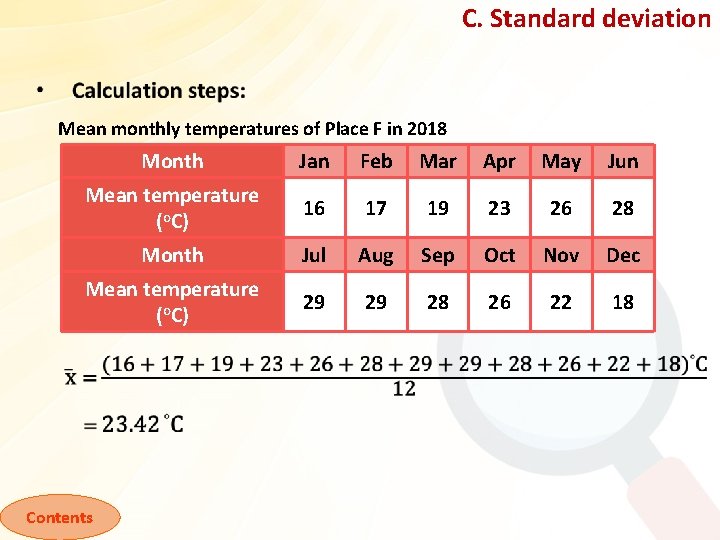
C. Standard deviation Mean monthly temperatures of Place F in 2018 Month Jan Feb Mar Apr May Jun Mean temperature (o. C) 16 17 19 23 26 28 Month Jul Aug Sep Oct Nov Dec Mean temperature (o. C) 29 29 28 26 22 18 Contents

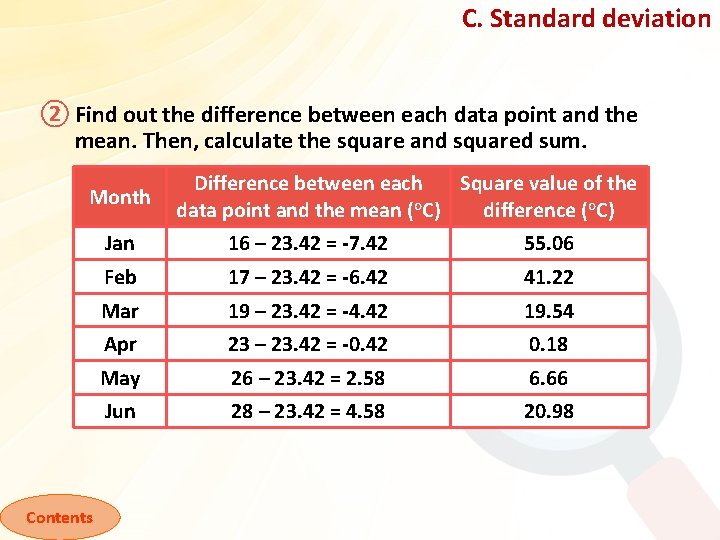
C. Standard deviation ② Find out the difference between each data point and the mean. Then, calculate the square and squared sum. Month Contents Difference between each Square value of the data point and the mean (o. C) difference (o. C) Jan 16 – 23. 42 = -7. 42 55. 06 Feb 17 – 23. 42 = -6. 42 41. 22 Mar 19 – 23. 42 = -4. 42 19. 54 Apr 23 – 23. 42 = -0. 42 0. 18 May 26 – 23. 42 = 2. 58 6. 66 Jun 28 – 23. 42 = 4. 58 20. 98

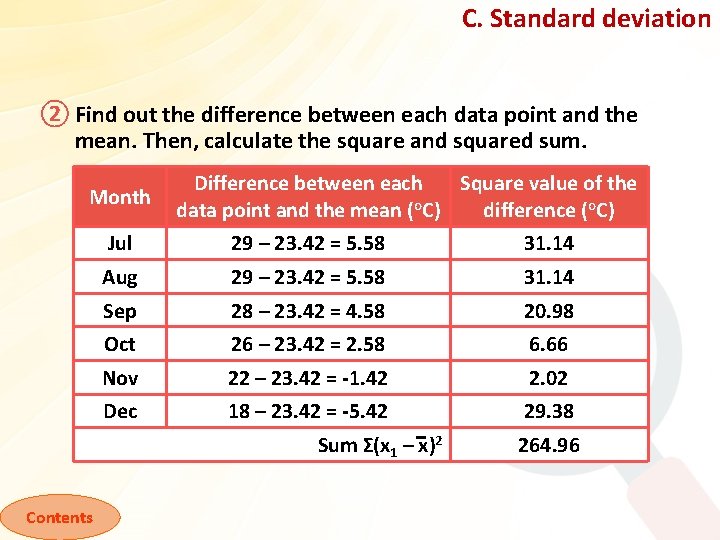
C. Standard deviation ② Find out the difference between each data point and the mean. Then, calculate the square and squared sum. Month Difference between each Square value of the data point and the mean (o. C) difference (o. C) Jul 29 – 23. 42 = 5. 58 31. 14 Aug 29 – 23. 42 = 5. 58 31. 14 Sep 28 – 23. 42 = 4. 58 20. 98 Oct 26 – 23. 42 = 2. 58 6. 66 Nov 22 – 23. 42 = -1. 42 2. 02 Dec 18 – 23. 42 = -5. 42 29. 38 Sum Σ(x 1 – x)2 Contents 264. 96

C. Standard deviation ③ Calculate the standard deviation (σ). ∴ The temperature data of Place F is centralised and close to the mean in 2018. Contents

C. Standard deviation Merits and demerits of standard deviation Merit Demerit • Make use of the value of each data • Complicated calculation point in the data set • Still affected by extreme • More accurately illustrate the values, but the sensitivity dispersion of data is lower than range • Less affected by changes of sampling method Contents

End