Content and Knowledge Management Laboratory B Data Mining

實驗室研究暨成果說明會 Content and Knowledge Management Laboratory (B) Data Mining Part Director: Anthony J. T. Lee Presenter: Wan-chuen Lin

Outline n Introduction of basic data mining concepts about our research topics n Brief description of doctoral research n Topic 1: Mining frequent itemsets with multidimensional constraints n Topic 2: Mining the inter-transactional association rules of multi-dimensional interval patterns n Topic 3: Inter-sequence association rules mining n Topic 4: Mining association rules among timeseries data 2

Introduction of Data Mining n Data mining is the task of discovering knowledge from large amounts of data. n One of the fundamental data mining problems, frequent itemset mining, covers a broad spectrum of mining topics, including association rules, sequential patterns, etc. n Frequent itemset mining is to discover all the itemsets whose supports in the database exceed a user-specified threshold. 3

Introduction of Association Rules n Association rule is of the form X Y, where X and Y are both frequent itemsets in the given database and X Y=. n The support of X Y is the percentage of transactions in the given database that contain both X and Y, i. e. , P(X Y). n The confidence of X Y is the percentage of transactions in the given database containing X that also contain Y, i. e. , P(Y|X). 4

Introduction of Sequential Patterns n A sequence is an ordered list of itemsets, and denoted by <s 1 s 2…sl>, where sj is an itemset. n sj is also called an element of the sequence, and denoted as (x 1 x 2…xm), where xk is an item. n The support of a sequence in a sequence database is the number of tuples containing . n A sequence is called a sequential pattern if support( ) min-support. 5

Algorithm for Mining Frequent Itemsets n Apriori n Candidate set generation-and–test n Level-wise: it iteratively generates candidate k-itemsets from previously found frequent (k-1)-itemsets, and then checks the supports of candidates to form frequent k-itemsets. n Lk-1 Ck Lk Join Support Check 6

Algorithm for Mining Frequent Itemsets (cont’d) n FP-growth n The method constructs a compressed frequent pattern tree, called FP-tree. n A divide-and-conquer strategy to recursively decompose the mining task into a set of smaller tasks in conditional databases, and concatenates the suffix itemset with the frequent itemsets generated from a conditional FP-tree. 7

Algorithm for Mining Sequential Patterns－Prefix. Span n It finds length-1 sequential patterns in the target database first, and partitions the database into smaller projected databases with prefix of each sequential pattern previously found. n The sequential patterns can be mined by constructing corresponding projected databases and mine each recursively. n It preserves the element order of each tuple in the mining process. 8

Brief Description of Doctoral Research n Mining calling path patterns in GSM networks n Two problems of mining calling path patterns n Mining PMFCPs n Mining periodic PMFCPs n Graph structures [(periodic) frequent calling path graph] and graph-based mining algorithms Based on a depth-first n No candidate paths are generated and the database is scanned only once if the whole graph structure can be held in the main memory. n 9

Brief Description of Doctoral Research (cont’d) n Bioinformatic data mining n Gene Clustering n Sequence comparisons, alignments and compression n n DNA sequence Protein sequence n Application n Phylogenetic tree to predict the function of a new protein n Relationship between DNA sequence & disease 10

Topic 1: Mining Frequent Itemsets with Multi-dimensional Constraints n Frequent itemset mining often generates a very large number of frequent itemsets. Only the subset of the frequent itemsets and association rules is of interest to users. n Users need additional post-processing to find useful ones. n n Constraint-based mining pushes user-specific constraints deep inside the mining process to improve performance. n With multi-dimensional items, constraints can be imposed on multiple dimensional attributes. 11

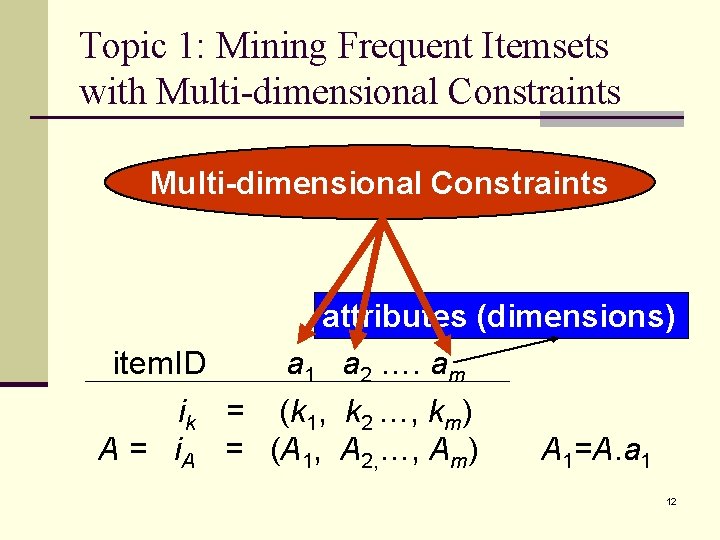
Topic 1: Mining Frequent Itemsets with Multi-dimensional Constraints attributes (dimensions) item. ID a 1 a 2 …. am ik = (k 1, k 2 …, km) A = i. A = (A 1, A 2, …, Am) A 1=A. a 1 12

Topic 1: Mining Frequent Itemsets with Multi-dimensional Constraints n Multi-dimensional constraints can be categorized according to constraint properties. n anti-monotone, convertible and inconvertible n It can be also classified according to the number of sub-constraints included. Single constraint against multiple dimensions, Ex: max(S. cost) min(S. price) n Conjunction and/or disjunction of multiple subconstraints, Ex: (C 1: S. cost v 1) (C 2: S. price v 2) n 13

Topic 1: Mining Frequent Itemsets with Multi-dimensional Constraints n We extend constraints to place over multi- dimensional itemsets and develop algorithms for mining frequent itemsets with multidimensional constraints by extension of CFG (Constrained Frequent Pattern Growth), n Overview of our algorithm Phase 1: Frequency check n Phase 2: Constraint check n Phase 3: Conditional database construction n 14

Example: Cam max(S. cost) min(S. price) A-conditional Database BECA BEA DA BDE BDECA BEC BDEC BDC Frequent items: B, D, E, C, A C(BDECA)=false C(B)=true C(D)=true C(E)=true BEC BE D BD BDEC Frequent items: B, D, E, C C(BDECA)=false C(BA)=false C(EA)=true C(DA)=true C(CA)=false C(C)=true C(A)=true EA-conditional Database D Frequent items: 15

Topic 2: Mining Inter-transactional Association Rules of Multi-dimensional Interval Patterns n Transaction could be the items bought by the same customer, the events happened on the same day, and so on. n Intra-transactional association rules: associations among items within the same transaction. n Ex: buy (X, diapers) => buy (X, beer) [support=80%] n Inter-transactional association rules: association relations among different transactions. n Ex: If the prices of IBM and SUN go up, Microsoft’s 16 will most likely [80%] increases the next day.

Topic 2: Mining Inter-transactional Association Rules of Multi-dimensional Interval Patterns n Interval data are different from the point data in that they occupy regions of non-zero size. n Multi-dimensional Intervals can be represented as line segments (1 -D), rectangles (2 -D), hyper-cubes (n-D), etc. n Extended item: denoted as (Location)<Size> n Reference point: the smallest (Location) among all (Location)<Size>. n Maxspan: a sliding window; only associations covered by it are considered. 17

Example n There are two cubes in the 3 -dimensional space: 0, 2, 1<1, 1, 1> and 1, 1, 0<2, 2, 1>. n Reference point: (0, 1, 0) n The two items are denoted as 0, 1, 1<1, 1, 1> and 1, 0, 0<2, 2, 1>. 0, 2, 1<1, 1, 1> 1, 1, 0<2, 2, 1> 18

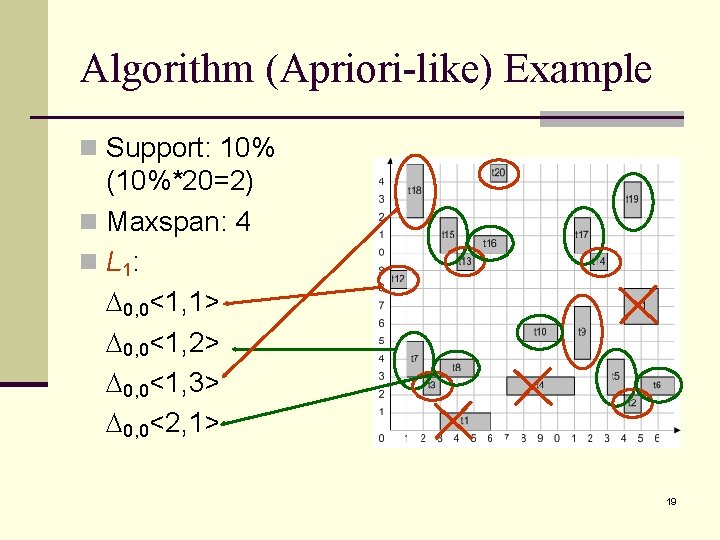
Algorithm (Apriori-like) Example n Support: 10% (10%*20=2) n Maxspan: 4 n L 1: 0, 0<1, 1> 0, 0<1, 2> 0, 0<1, 3> 0, 0<2, 1> 19

Algorithm (Apriori-like) Example (cont’d) n Remind: Apriori-like algorithm n Lk-1 Ck Support Check Join n L 2: Lk { 0, 0<1, 1>, 1, 1<2, 1>}, { 1, 0<1, 1>, 0, 1<1, 2>}, { 0, 0<1, 2>, 2, 0<2, 1>}, { 0, 0<1, 3>, 3, 0<1, 2>} n L 3: { 3, 0<1, 1>, 2, 1<1, 2>, 0, 3<1, 3>} { 1, 0<1, 1>, 0, 1<1, 2>, 2, 1<2, 1>} { 3, 0<1, 1>, 0, 3<1, 3>, 4, 1<2, 1>} { 2, 0<1, 2>, 0, 2<1, 3>, 4, 0<2, 1>} n L 4: { 0, 3<1, 3>, 4, 1<2, 1>, 2, 1<1, 2>, 3, 0<1, 1>} 20

Topic 3: Inter-sequence Association Rules Mining n Inter-sequence model Transaction ID : 1 2 3 4 5 6 7 8 9 10 Transaction Time : <ceacc(ce)> <ab> <acc> <bc> <dd(ac)bd> <> <b(ab)cc> <e(ac)bac> <(bc)cb> <c(ab)d(ad)> 21

Topic 3: Inter-sequence Association Rules Mining (cont’d) n Extended sequence (denote asΔt<s 1 s 2…sl>): a sequence s = <s 1 s 2…sl> at time pointΔt. n Algorithm: Step 1: Use Prefix. Span to find all sequential patterns n Step 2: Use an Apriori-like method to check if some extended sequence set is large n n Use L-bucket (List-bucket) & C-bucket (candidate-bucket) to improve mining efficiency. 22

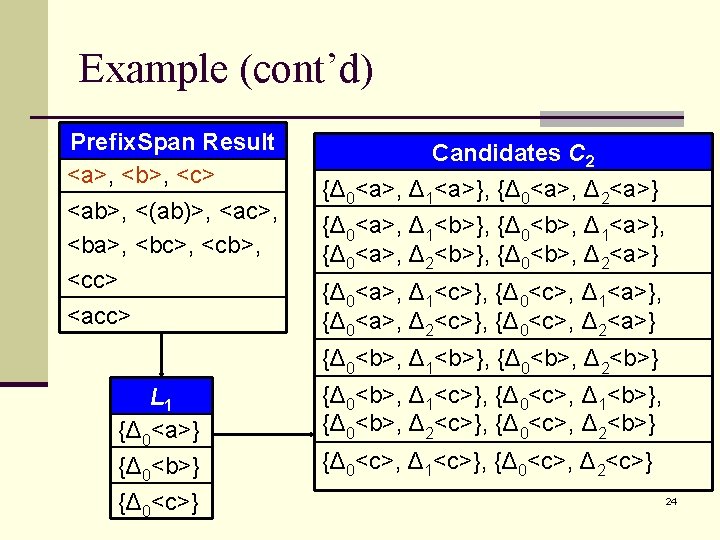
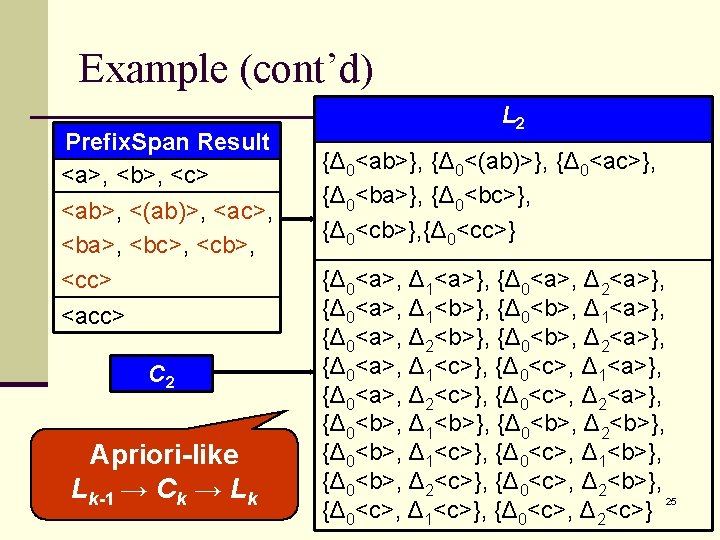
Example n min_support = 3 n maxspan = 2 Prefix. Span Sequential Patterns: –<a>, <b>, <c> –<ab>, <(ab)>, <ac>, <ba>, <bc>, <cb>, <cc> –<acc> The database Tran. ID Tran. Time Sequence 1 1 <c(ab)d(ad)> 2 2 <(bc)cb> 3 3 <e(ac)bac> 4 4 <b(ab)cc> 5 5 <(ab)c> 6 6 <dd(ac)bd> 7 7 <bc> 8 8 <acc> 9 9 <ab> 10 10 <ceacc(ce)> 23

Topic 4: Mining Association Rules among Time-series Data n A line is an ordered and continuous list in the form {t 1, t 2, …, tm} describing the property of the subject along the time. n Step 1: find the frequent lines and points in each line-set. (Apriori-like algorithm) n Step 2: use those frequent-set combination to find the associations among them. (intertransaction association rules) 26

Topic 4: Mining Association Rules among Time-series Data 27

Time-series Data Approximation n For the algorithm’s efficiency n Equally partition the fluctuation rate into several classes. 28

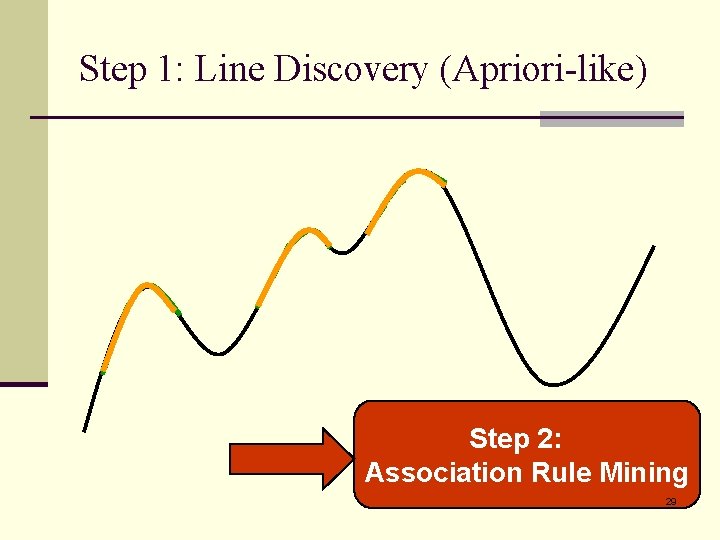
Step 1: Line Discovery (Apriori-like) Step 2: Association Rule Mining 29

Data Mining Part Thank You!