Contemporary Mathematics Topic 17 Groups and Fields Abstract

Contemporary Mathematics Topic 17: Groups and Fields

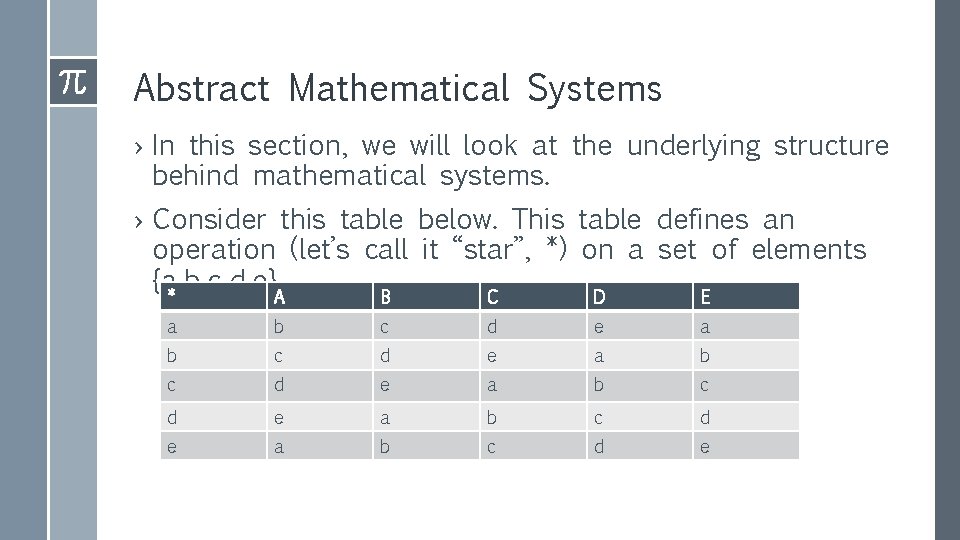
Abstract Mathematical Systems › In this section, we will look at the underlying structure behind mathematical systems. › Consider this table below. This table defines an operation (let’s call it “star”, *) on a set of elements {a, b, c, d, e} * A B C D E a b c d e a b c d e

Example 1: › Use the Table on slide 2 to answer the following: › A) a*b › B) b *e › C) d *b › D) (a *b) * c

Closure › A set A is closed under an operation * if, for all a and b in A, a *b is also in A. › For example, if a set D = {0, 1}, this set would be closed under multiplication. (See if you can show that. ) › However, the set E = {1, 2} is NOT closed under multiplication. (See if you can show that. )

Associativity › An operation * is defined on a set A to be associative if, for all a, b, and c in A, (a*b)*c = a*(b*c) › Look at the Table on slide 2. Sis (a *b) *d = a * (b*d)? › Does this mean * on set {a, b, c, d, e} in Slide 2 is associative?

Commutativity › Am operation * is defined on a set A to be commutative if, for every a and b in A, a*b = b*a. › Check whether each of the following are commutative (one is, one isn’t): › The multiples of 3 under addition › The odd numbers under subtraction

Identity › An element e in a set A is said to be an identity for the operation * if, for each element x in A, x* e = e * x = x › Look in the Table on slide 2. Show that the element e is an identity for * under {a, b, c, d, e}

Inverse › If a and b are in A, we say that a is the inverse of b under * if a*b = e = b*a, where e is the identity. › In the Table on slide 2, find the inverse of a and the inverse of b.

Distributive Property › An operation * defined on a set A is said to be distributive over the operation # if, for all a, b, and c in A, we have a*(b # c) = (a * b) # (a *c)

Groups › A group is a mathematical system consisting of a set of elements S and an operation * with the following 4 properties: › Closure › Associativity › Identity › Inverse › If the set is also commutative, it is called a commutative group.

Example 2: › Show whether the set S = {0, 1, 2, 3, 4}, along with multiplication modulo 5, forms a commutative group. › Omit 0 from the list above. What changes now?

Fields › A field is a mathematical system consisting of a set S and two operations, say * and #, defined on S and having the following properties: › Closure › Associative › Identity › Inverse (not having inverse for identity with * is okay) › Commutative › Distributive

Example 3: › Let S = {Odd numbers, Even numbers} and let + and x be the typical multiplication and addition from the real numbers. Does the set S with + and x operations form a field? Show your work.