Contemporary Mathematics Topic 14 Number Systems with Bases

Contemporary Mathematics Topic 14: Number Systems with Bases Other Than 10

Bases › As we have seen, in a positional number system, the symbols are given value based on their position. To give the symbols value, an arbitrary base must be chosen. › In the Hindu-Arabic numeral system, base 10 is chosen, probably because it was convenient to use your fingers as an aid in counting. › There are situations and applications, though, where it is convenient or even necessary to use bases other than 10. (Recall the Babylonians had base 60. ) This has given rise to several other number systems in common use.

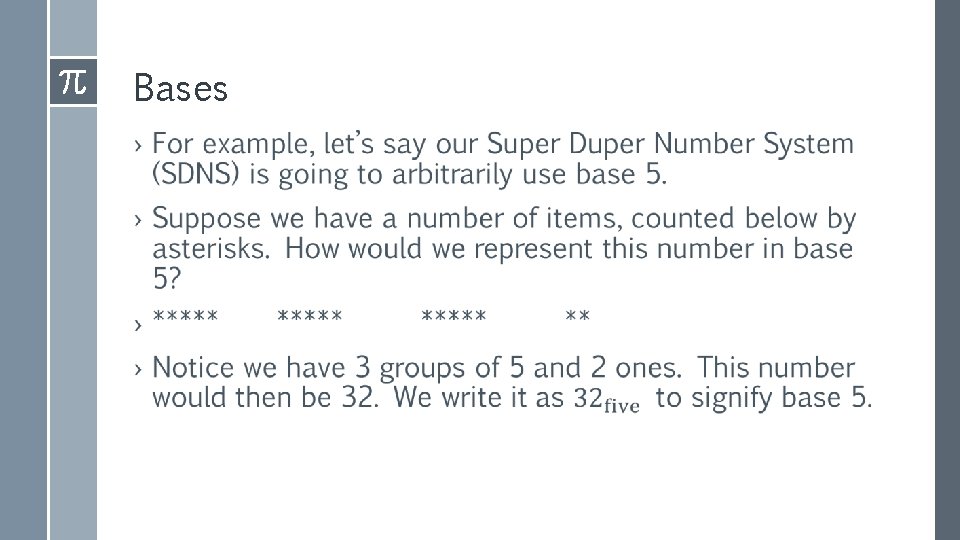
Bases ›

Bases › One way of visualizing this is to understand what happens in our own base 10 when we reach 10 “things”. › 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …. what comes next? › To represent 10, we start over the ones digit back at 0 and to the left of it, we add a new place value for the tens place and make it a “ 1”, hence we get “ 10”. › Now, counting continues until we get to 99, then 9 and 9 flip over to “ 0” and to their left, we add a new place value for the hundreds and give it a 1 to becomes “ 100”. › And so on…

Bases ›

Example 1: › Write the number 27 in base 8, 5, 7, and 16.

Translating to Base 10 ›

Binary ›

Hexadecimal ›

Example 2: ›

Converting from Base 10 ›

Example 3: › Convert each of the following to the given base: › A) 567 to octal › B) 1027 to binary › C) 65, 412 to hexadecimal