CONSTRUO DE GRFICOS Fsica Experimental 01 Grfico em

CONSTRUÇÃO DE GRÁFICOS Física Experimental 01

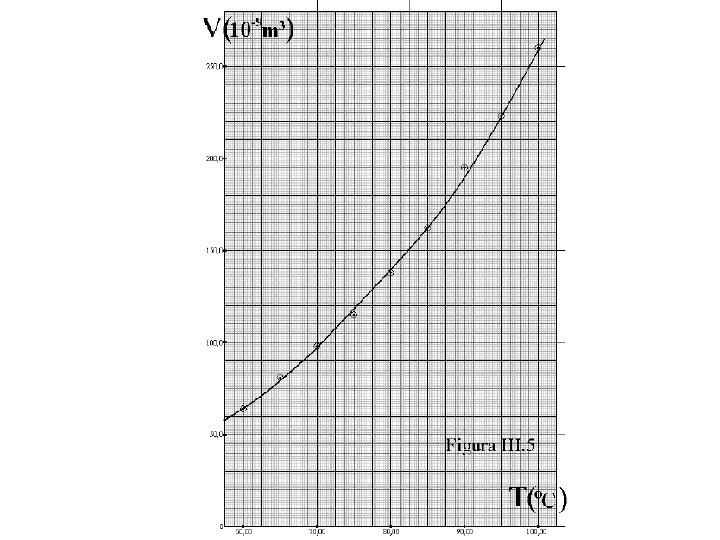
Gráfico em papel milimetrado Através do exemplo abaixo, vejamos como se constrói um gráfico, usando o papel milimetrado. V (109 m 3 ) 64, 1 80, 7 97, 8 114, 9 138, 0 162, 5 195, 0 223, 3 260, 0 T(0 C) 60, 00 65, 00 70, 00 75, 00 80, 00 85, 00 90, 00 95, 00 100, 00

Coeficiente de Correlação de Pearson Este coeficiente pode variar de -1 a +1 e mostra a intensidade da relação linear entre as duas variáveis estudadas.

O Quadrado da correlação R 2 Mostra o percentual da variância de uma das variáveis que pode ser explicado a partir do valor da outra (coeficiente de determinação).

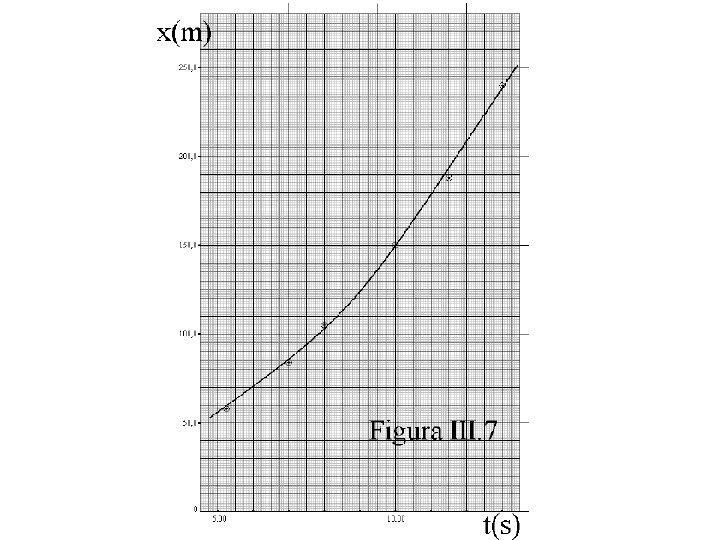
Linearização Considere que foram realizadas medidas do movimento retilíneo de um móvel que se desloca ao longo de uma estrada. Obteve-se um conjunto de valores de sua posição e do tempo, que foram anotados na tabela abaixo. X(m) 58, 0 84, 0 105, 0 150, 0 188, 0 240, 0 t(s) 5, 25 7, 00 8, 00 11, 50 13, 00 10, 00

Linearização A curva obtida nesse gráfico é uma parábola, e obedece a uma equação geral do tipo: y(x) = a 2 x² + a 1 x + a 0 , no caso x(t) = εt 2 + γ, onde os coeficientes ε e γ são constantes. Como determinar gráficamente as constantes ε eγ? Usando a técnica da linearização.

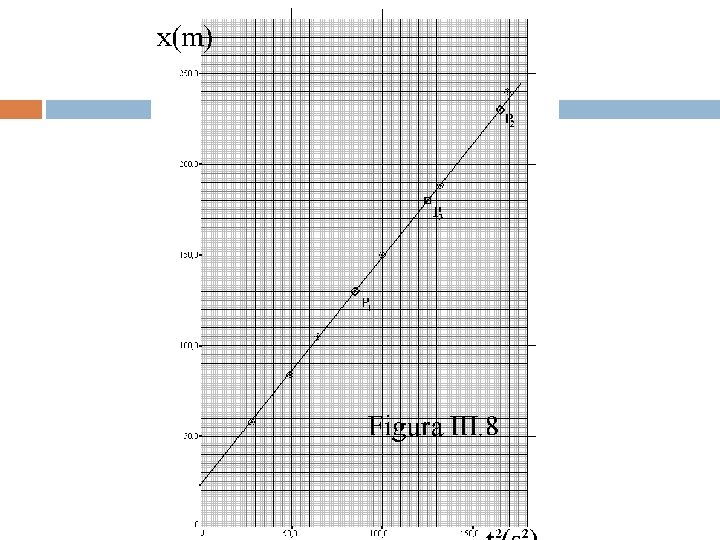
Linearização Comparação com a equação reduzida da reta x(t) = εt 2 + γ y'(x') = a'x' + b'. Obtemos, x(t) = y'(x'); ε = a'; t² = x'; γ = b' Sabemos que o gráfico “ y'(x') versus x' ” é uma reta. x(t) versus t ⇒ gráfico não linear y'(x') versus x' ⇒ x(t) versus t² ⇒ gráfico line

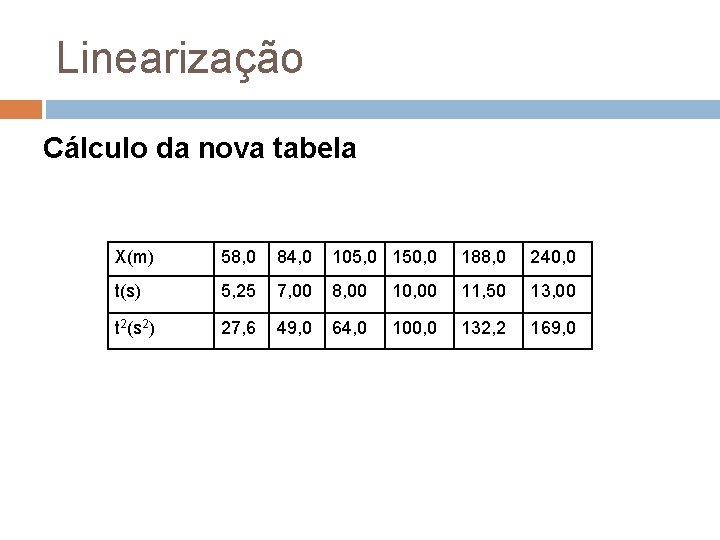
Linearização Cálculo da nova tabela X(m) 58, 0 84, 0 105, 0 150, 0 188, 0 240, 0 t(s) 5, 25 7, 00 8, 00 10, 00 11, 50 13, 00 t 2(s 2) 27, 6 49, 0 64, 0 100, 0 132, 2 169, 0

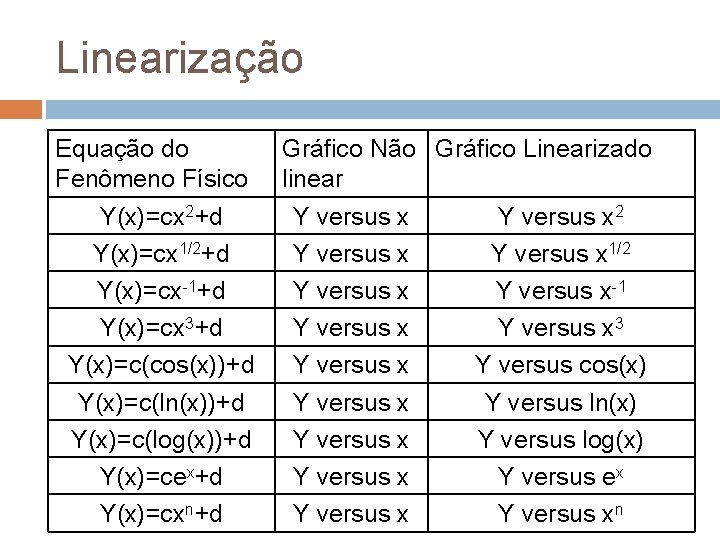
Linearização Equação do Fenômeno Físico Y(x)=cx 2+d Y(x)=cx 1/2+d Y(x)=cx-1+d Y(x)=cx 3+d Y(x)=c(cos(x))+d Y(x)=c(ln(x))+d Y(x)=c(log(x))+d Y(x)=cex+d Y(x)=cxn+d Gráfico Não Gráfico Linearizado linear Y versus x 2 Y versus x 1/2 Y versus x-1 Y versus x 3 Y versus x Y versus cos(x) Y versus x Y versus ln(x) Y versus x Y versus log(x) Y versus x Y versus ex Y versus xn

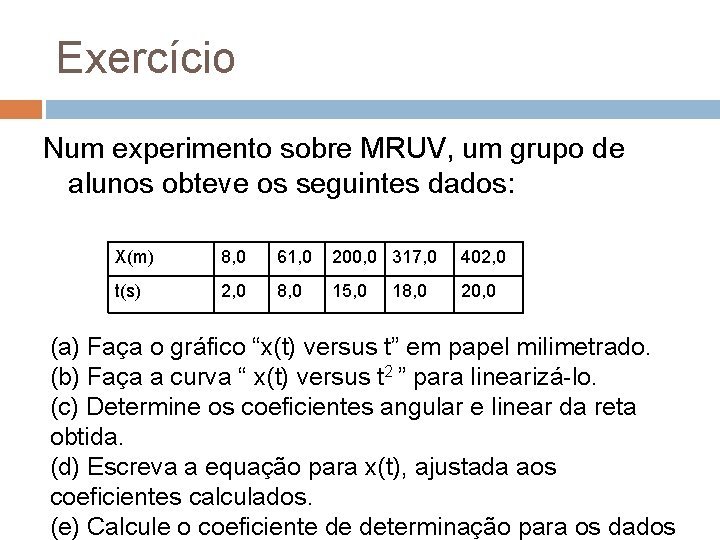
Exercício Num experimento sobre MRUV, um grupo de alunos obteve os seguintes dados: X(m) 8, 0 61, 0 200, 0 317, 0 402, 0 t(s) 2, 0 8, 0 15, 0 20, 0 18, 0 (a) Faça o gráfico “x(t) versus t” em papel milimetrado. (b) Faça a curva “ x(t) versus t 2 ” para linearizá-lo. (c) Determine os coeficientes angular e linear da reta obtida. (d) Escreva a equação para x(t), ajustada aos coeficientes calculados. (e) Calcule o coeficiente de determinação para os dados