Constructive Computer Architecture Sequential Circuits Circuits with state

Constructive Computer Architecture Sequential Circuits: Circuits with state Arvind Computer Science & Artificial Intelligence Lab. Massachusetts Institute of Technology September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -1

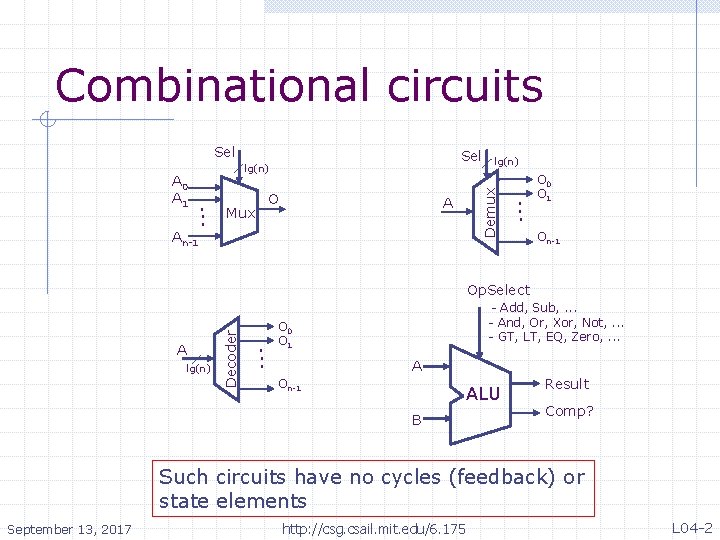
Combinational circuits Sel An-1 . . . O Mux A lg(n) Demux A 0 A 1 Sel lg(n) . . . O 0 O 1 On-1 A lg(n) Decoder Op. Select . . . - Add, Sub, . . . - And, Or, Xor, Not, . . . - GT, LT, EQ, Zero, . . . O 0 O 1 A On-1 ALU B Result Comp? Such circuits have no cycles (feedback) or state elements September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -2

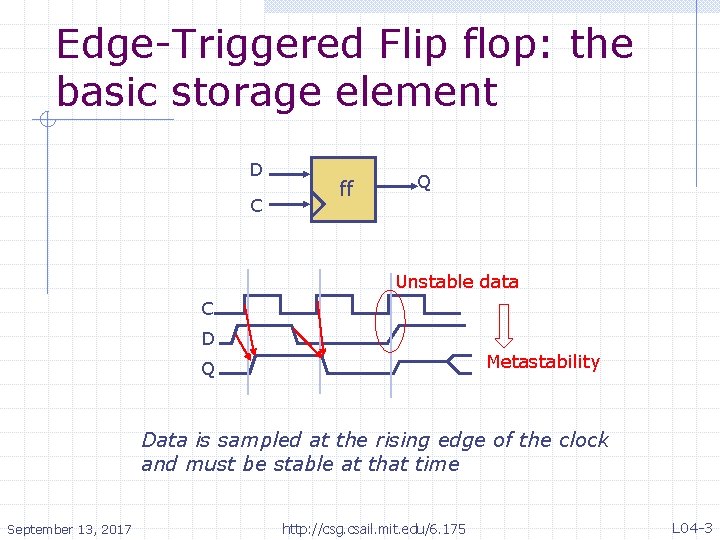
Edge-Triggered Flip flop: the basic storage element D C ff Q Unstable data C D Metastability Q Data is sampled at the rising edge of the clock and must be stable at that time September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -3

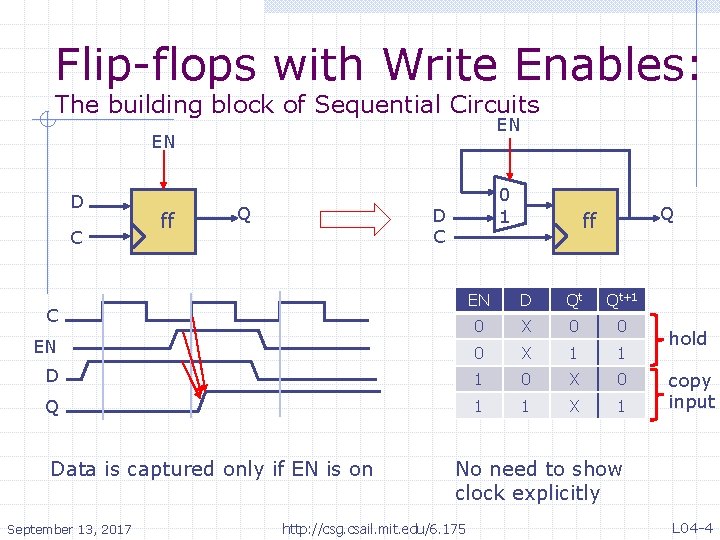
Flip-flops with Write Enables: The building block of Sequential Circuits EN EN D C ff Q 0 1 D C Q ff EN D Qt Qt+1 0 X 0 0 0 X 1 1 D 1 0 X 0 Q 1 1 X 1 C EN Data is captured only if EN is on September 13, 2017 hold copy input No need to show clock explicitly http: //csg. csail. mit. edu/6. 175 L 04 -4

Registers D D D D ff ff Q Q Q Q En C Register: A group of flip-flops with a common clock and enable Register file: A group of registers with a common clock, input and output port(s) September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -5

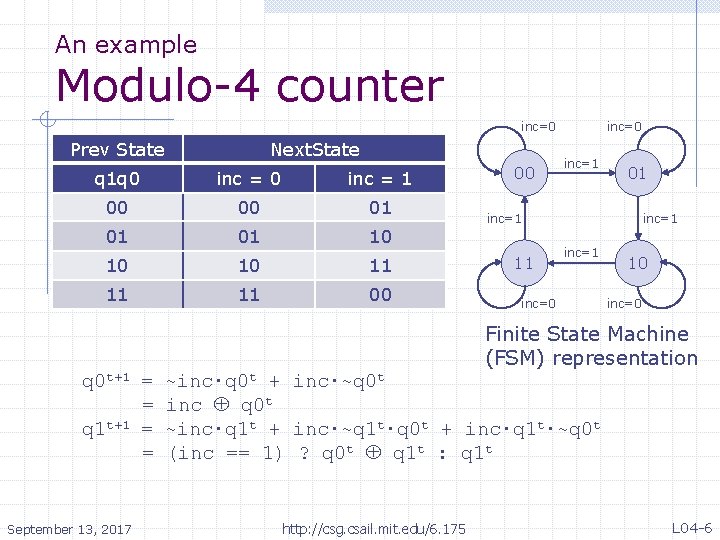
An example Modulo-4 counter inc=0 Prev State Next. State q 1 q 0 inc = 1 00 00 01 01 01 10 10 10 11 11 11 00 00 inc=1 01 inc=1 11 inc=1 inc=0 10 inc=0 Finite State Machine (FSM) representation q 0 t+1 = = q 1 t+1 = = September 13, 2017 ~inc∙q 0 t + inc∙~q 0 t inc q 0 t ~inc∙q 1 t + inc∙~q 1 t∙q 0 t + inc∙q 1 t∙~q 0 t (inc == 1) ? q 0 t q 1 t : q 1 t http: //csg. csail. mit. edu/6. 175 L 04 -6

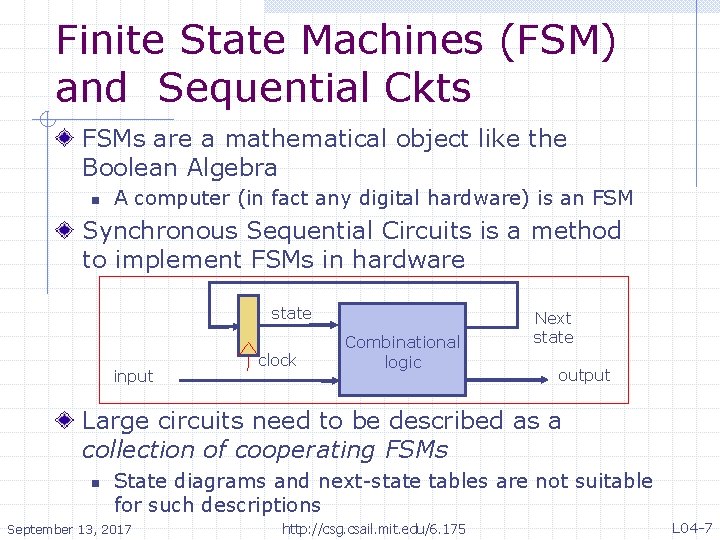
Finite State Machines (FSM) and Sequential Ckts FSMs are a mathematical object like the Boolean Algebra n A computer (in fact any digital hardware) is an FSM Synchronous Sequential Circuits is a method to implement FSMs in hardware state input clock Combinational logic Next state output Large circuits need to be described as a collection of cooperating FSMs n State diagrams and next-state tables are not suitable for such descriptions September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -7

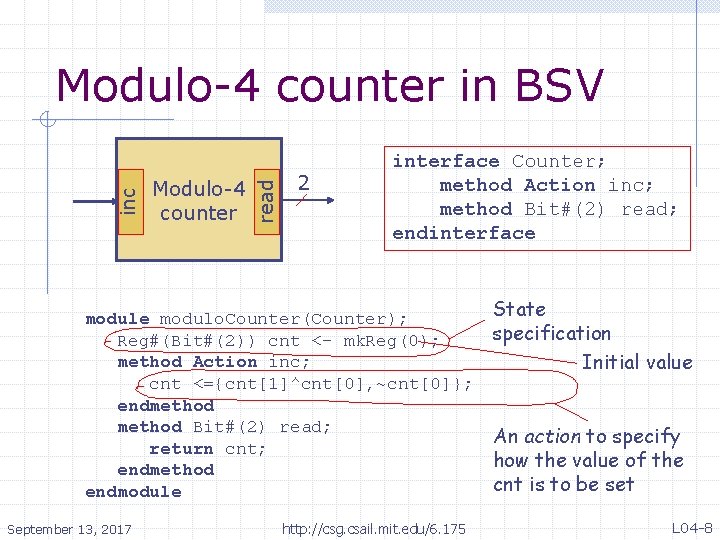
Modulo-4 counter read inc Modulo-4 counter in BSV 2 interface Counter; method Action inc; method Bit#(2) read; endinterface modulo. Counter(Counter); Reg#(Bit#(2)) cnt <- mk. Reg(0); method Action inc; cnt <={cnt[1]^cnt[0], ~cnt[0]}; endmethod Bit#(2) read; return cnt; endmethod endmodule September 13, 2017 http: //csg. csail. mit. edu/6. 175 State specification Initial value An action to specify how the value of the cnt is to be set L 04 -8

Modules A module in BSV is like a class definition in Java or C++ n n It has internal state The internal state can only be read and manipulated by the (interface) methods An action specifies which state elements are to be modified Actions are atomic -- either all the specified state elements are modified or none of them are modified (no partially modified state is visible) interface Counter; method Action inc; method Bit#(2) read; endinterface September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -9

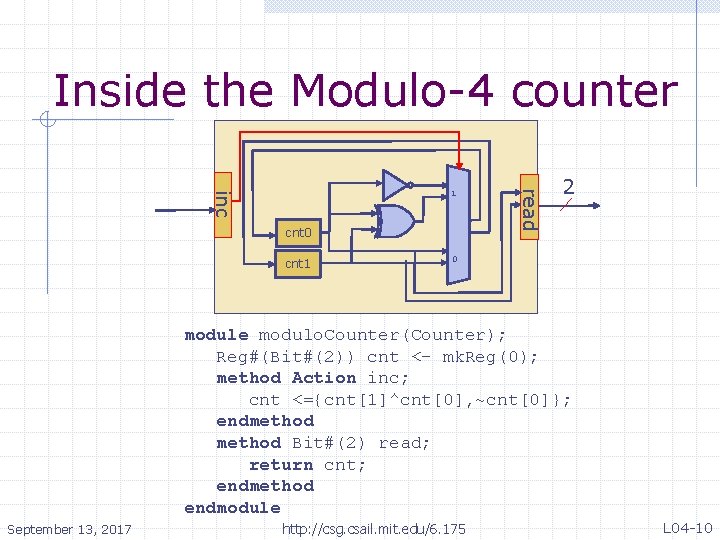
Inside the Modulo-4 counter cnt 0 cnt 1 read inc 1 2 0 module modulo. Counter(Counter); Reg#(Bit#(2)) cnt <- mk. Reg(0); method Action inc; cnt <={cnt[1]^cnt[0], ~cnt[0]}; endmethod Bit#(2) read; return cnt; endmethod endmodule September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -10

Examples September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -11

A hardware module for computing GCD Euclid’s algorithm for computing the Greatest Common Divisor (GCD): 15 6 9 6 subtract 3 6 subtract 6 3 swap 3 3 subtract 0 3 subtract answer gcd (a, b) = if a==0 then b \ stop else if a>=b then gcd(a-b, b) \ subtract else gcd (b, a) \ swap September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -12

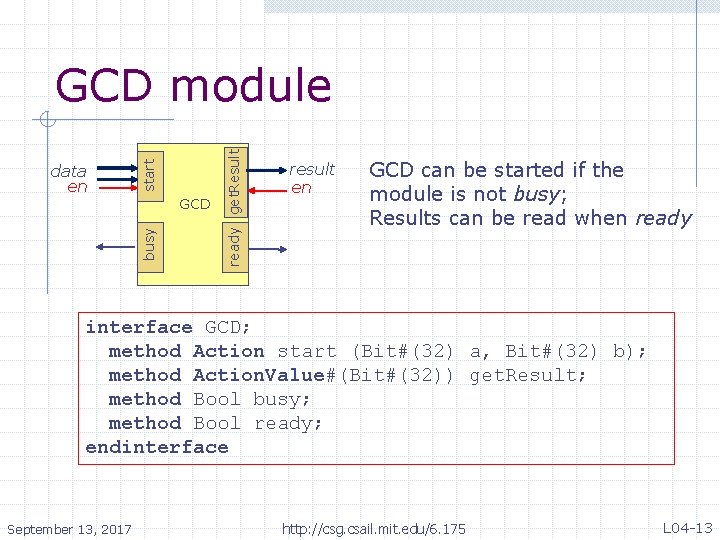
ready get. Result GCD busy data en start GCD module result en GCD can be started if the module is not busy; Results can be read when ready interface GCD; method Action start (Bit#(32) a, Bit#(32) b); method Action. Value#(Bit#(32)) get. Result; method Bool busy; method Bool ready; endinterface September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -13

GCD in BSV module mk. GCD (GCD); Reg#(Bit#(32)) x <- mk. Reg(0); Reg#(Bit#(32)) y <- mk. Reg(0); Reg#(Bool) busy_flag <- mk. Reg(False); rule gcd; if (x >= y) begin x <= x – y; end //subtract else if (x != 0) begin x <= y; y <= x; end //swap endrule method Action start(Bit#(32) a, Bit#(32) b); Assume b /= 0 x <= a; y <= b; busy_flag <= True; endmethod Action. Value#(Bit#(32)) get. Result; busy_flag <= False; return y; start should be called only endmethod if the module is not busy; method busy = busy_flag; get. Result should be called method ready = x==0; only when ready is true. endmodule September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -14

Rule A module may contain rules parallel composition of actions rule gcd; if (x >= y) begin x <= x – y; end //subtract else if (x != 0) begin x <= y; y <= x; end //swap endrule A rule is a collection of actions, which invoke methods All actions in a rule execute in parallel A rule can execute any time and when it ty i ic executes all of its actions must execute om at September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -15

Parallel Composition of Actions & Double-Writes rule one; y <= 3; x <= 5; x <= 7; endrule Double write rule two; y <= 3; if (b) x <= 7; else x <= 5; endrule No double write rule three; y <= 3; x <= 5; if (b) x <= 7; endrule Possibility of a double write Parallel composition, and consequently a rule containing it, is illegal if a double-write possibility exists The BSV compiler rejects a program if it there is a possibility of a double write September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -16

Defining FIFOs and it’s uses September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -17

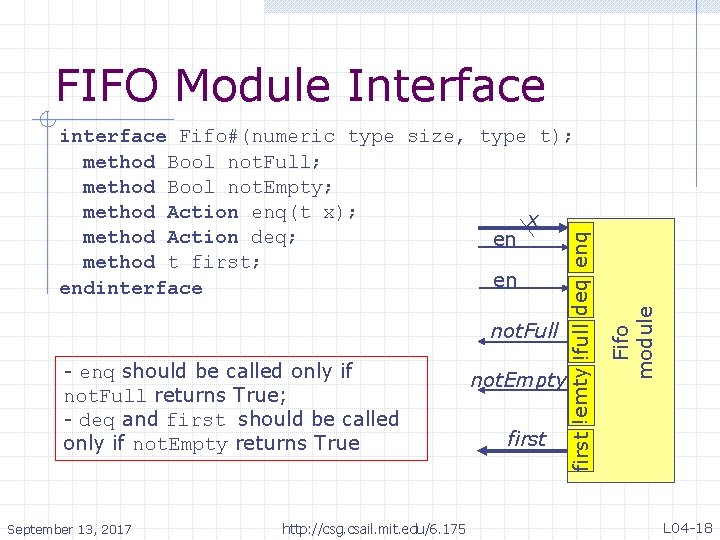
FIFO Module Interface - enq should be called only if not. Full returns True; - deq and first should be called only if not. Empty returns True September 13, 2017 http: //csg. csail. mit. edu/6. 175 not. Empty first Fifo module not. Full first !emty !full deq enq interface Fifo#(numeric type size, type t); method Bool not. Full; method Bool not. Empty; method Action enq(t x); x method Action deq; en method t first; en endinterface L 04 -18

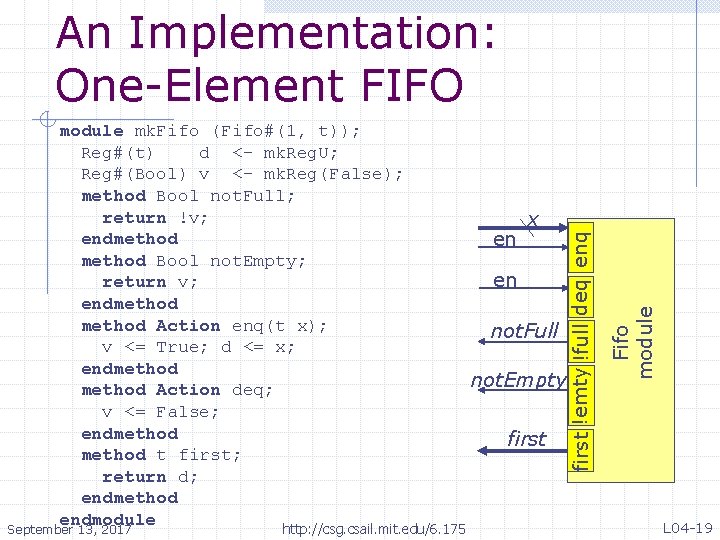
first !emty !full deq enq module mk. Fifo (Fifo#(1, t)); Reg#(t) d <- mk. Reg. U; Reg#(Bool) v <- mk. Reg(False); method Bool not. Full; return !v; x endmethod en method Bool not. Empty; en return v; endmethod Action enq(t x); not. Full v <= True; d <= x; endmethod not. Empty method Action deq; v <= False; endmethod first method t first; return d; endmethod endmodule http: //csg. csail. mit. edu/6. 175 September 13, 2017 Fifo module An Implementation: One-Element FIFO L 04 -19

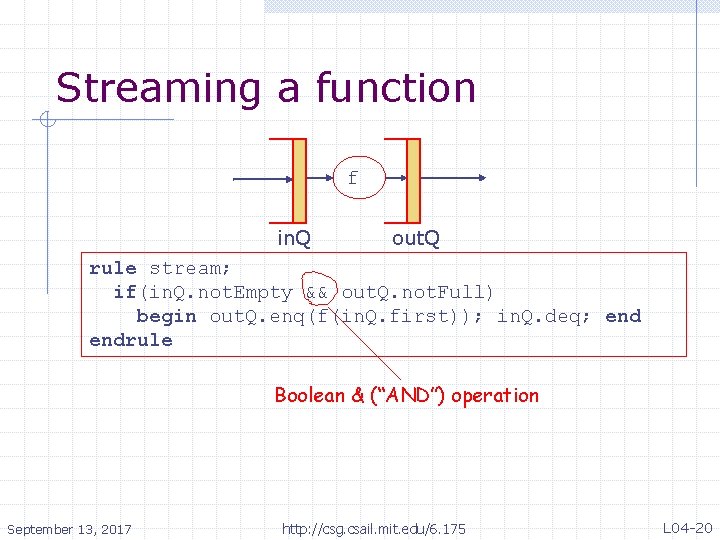
Streaming a function f in. Q out. Q rule stream; if(in. Q. not. Empty && out. Q. not. Full) begin out. Q. enq(f(in. Q. first)); in. Q. deq; endrule Boolean & (“AND”) operation September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -20

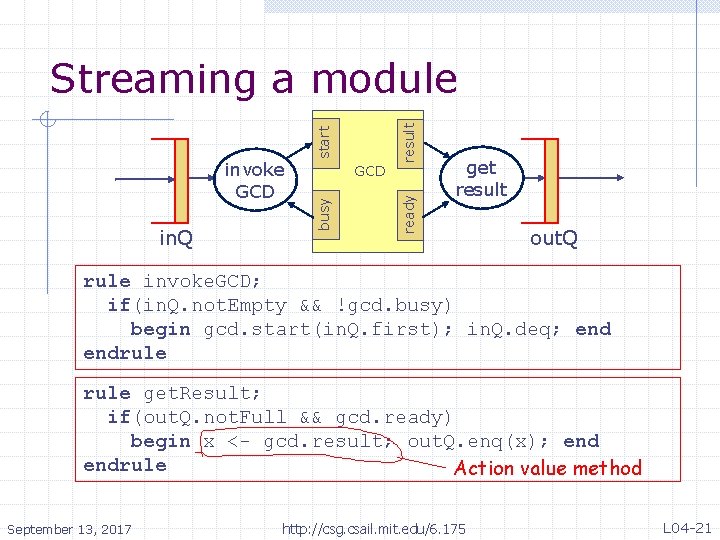
result ready in. Q GCD busy invoke GCD start Streaming a module get result out. Q rule invoke. GCD; if(in. Q. not. Empty && !gcd. busy) begin gcd. start(in. Q. first); in. Q. deq; endrule get. Result; if(out. Q. not. Full && gcd. ready) begin x <- gcd. result; out. Q. enq(x); endrule Action value method September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -21

Switch red messages go into red. Q, green into green. Q in. Q red. Q switch green. Q red messages go into red. Q, green into green. Q rule switch; if (in. Q. first. color == Red) begin red. Q. enq(in. Q. first. value); in. Q. deq; end else begin green. Q. enq(in. Q. first. value); in. Q. deq; endrule The code is not correct because it does not include tests for empty in. Q or full red. Q or full green. Q conditions! September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -22

Switch with empty/full tests on queues - 1 in. Q red. Q switch green. Q rule switch; if (in. Q. first. color == Red) begin red. Q. enq(in. Q. first. value); in. Q. deq; end else begin green. Q. enq(in. Q. first. value); in. Q. deq; endrule first and deq operations can be performed only if in. Q is not empty September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -23

Switch with empty/full tests on queues -2 in. Q red. Q switch green. Q rule switch; if (in. Q. not. Empty) if (in. Q. first. color == Red) begin red. Q. enq(in. Q. first. value); in. Q. deq; end else begin green. Q. enq(in. Q. first. value); in. Q. deq; endrule When can an enq operation be performed on red. Q? September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -24

Switch with empty/full tests on queues in. Q red. Q switch green. Q rule switch; if (in. Q. not. Empty) if (in. Q. first. color == Red) begin 1 if (red. Q. not. Full) begin 2 red. Q. enq(in. Q. first. value); in. Q. deq; end 2 end 1 else begin 3 if (green. Q. not. Full) begin 4 green. Q. enq(in. Q. first. value); in. Q. deq; end 4 end 3 endrule September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -25

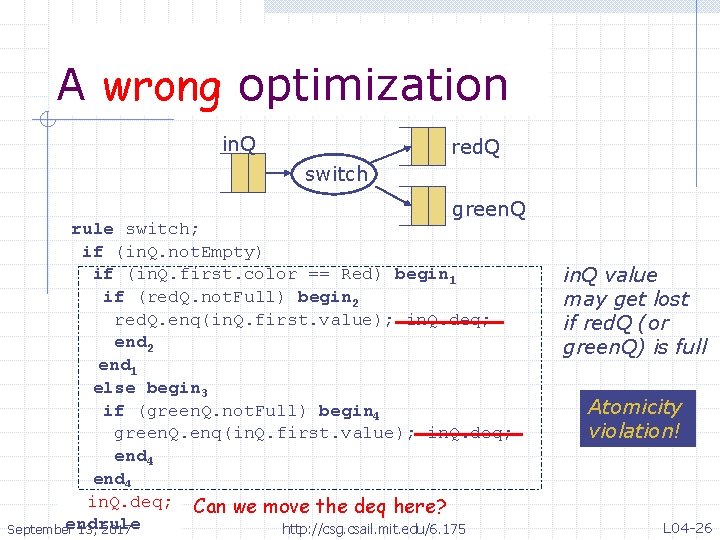
A wrong optimization An optimization in. Q red. Q switch green. Q rule switch; if (in. Q. not. Empty) if (in. Q. first. color == Red) begin 1 if (red. Q. not. Full) begin 2 red. Q. enq(in. Q. first. value); in. Q. deq; end 2 end 1 else begin 3 if (green. Q. not. Full) begin 4 green. Q. enq(in. Q. first. value); in. Q. deq; end 4 endrule in. Q. deq; Can we move the deq here? endrule http: //csg. csail. mit. edu/6. 175 September 13, 2017 in. Q value may get lost if red. Q (or green. Q) is full Atomicity violation! L 04 -26

Observations These sample programs are not very complex and yet it would have been tedious to express these programs in a state table or as a circuit directly The meaning of double-write errors is not standardized across Verilog tools Interface methods are not available in Verilog/VHDL September 13, 2017 http: //csg. csail. mit. edu/6. 175 L 04 -27