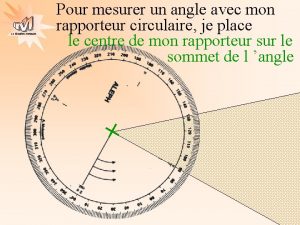
Constructions gomtriques lmentaires Avec rgle compas et rapporteur

Constructions géométriques élémentaires Avec règle, compas et rapporteur Constructions with straight edge and compass

INDEX – Constructions géométriques GÉNÉRAL Perpendiculaire: 3, 4 (numéro des pages) Parallèle: 10 Milieu et médiatrice: 4 Division du segment: 11 TRIANGLES Trois côtés: 13 Deux côtés et un angle: 15 Un côté et deux angles: 14 Trois angles: 14 Angles 60°, 45° et 30°: 7 Angle – Copie: 9 Angle – Addition et soustraction: 9 Rectangle: 16 Isocèle: 17, 18 Équilatéral: 8 Triangle: 13 Carré: 12 Carré inscrit dans le cercle: 12 Rectangle: 12 Parallélogramme: 10 Pentagone: 21 Hexagone: 8 Rosace: 8 Hauteurs (orthocentre): 4 Bissectrices (cercle inscrit): 6 Médianes (centre de gravité): 5 Médiatrices (cercle circonscrit): 5 Cercle inscrit: 6 Cercle circonscrit: 5 Cercles exinscrits: 6 Cercle - Centre: 19 Cercle par trois points: 5 Tangente au cercle: 20 2

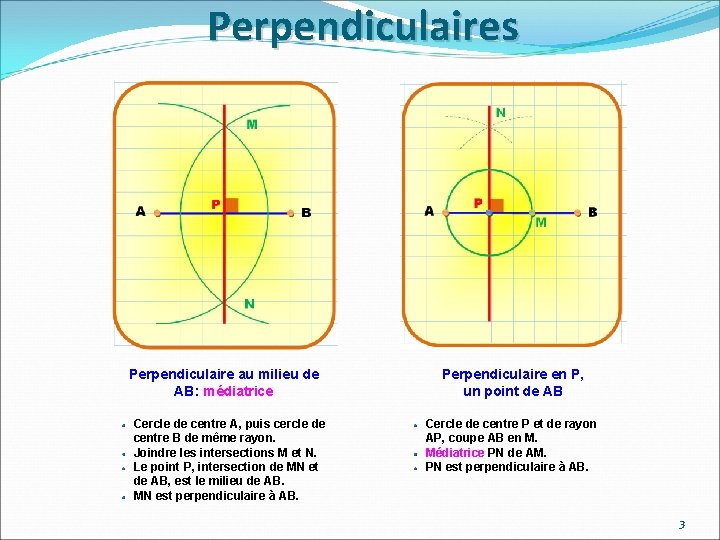
Perpendiculaires Perpendiculaire au milieu de AB: médiatrice Cercle de centre A, puis cercle de centre B de même rayon. Joindre les intersections M et N. Le point P, intersection de MN et de AB, est le milieu de AB. MN est perpendiculaire à AB. Perpendiculaire en P, un point de AB Cercle de centre P et de rayon AP, coupe AB en M. Médiatrice PN de AM. PN est perpendiculaire à AB. 3

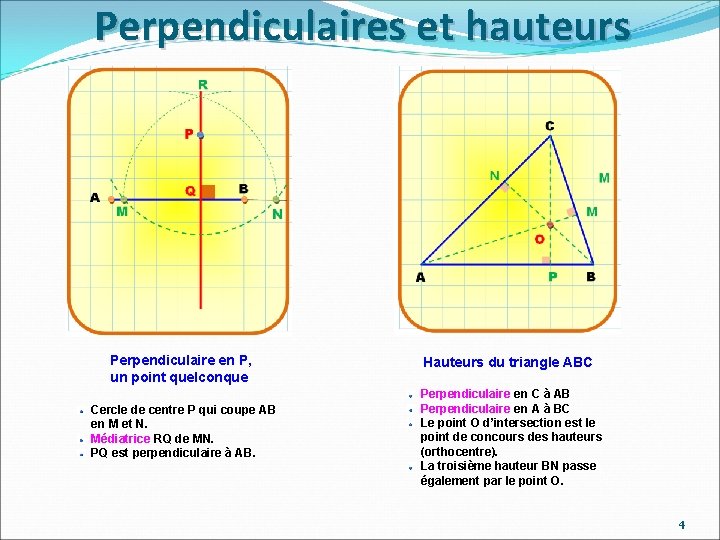
Perpendiculaires et hauteurs Perpendiculaire en P, un point quelconque Cercle de centre P qui coupe AB en M et N. Médiatrice RQ de MN. PQ est perpendiculaire à AB. Hauteurs du triangle ABC Perpendiculaire en C à AB Perpendiculaire en A à BC Le point O d’intersection est le point de concours des hauteurs (orthocentre). La troisième hauteur BN passe également par le point O. 4

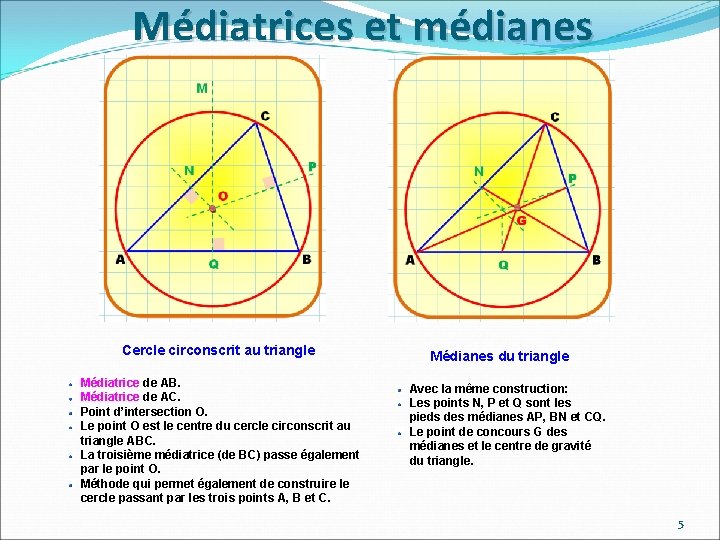
Médiatrices et médianes Cercle circonscrit au triangle Médiatrice de AB. Médiatrice de AC. Point d’intersection O. Le point O est le centre du cercle circonscrit au triangle ABC. La troisième médiatrice (de BC) passe également par le point O. Méthode qui permet également de construire le cercle passant par les trois points A, B et C. Médianes du triangle Avec la même construction: Les points N, P et Q sont les pieds des médianes AP, BN et CQ. Le point de concours G des médianes et le centre de gravité du triangle. 5

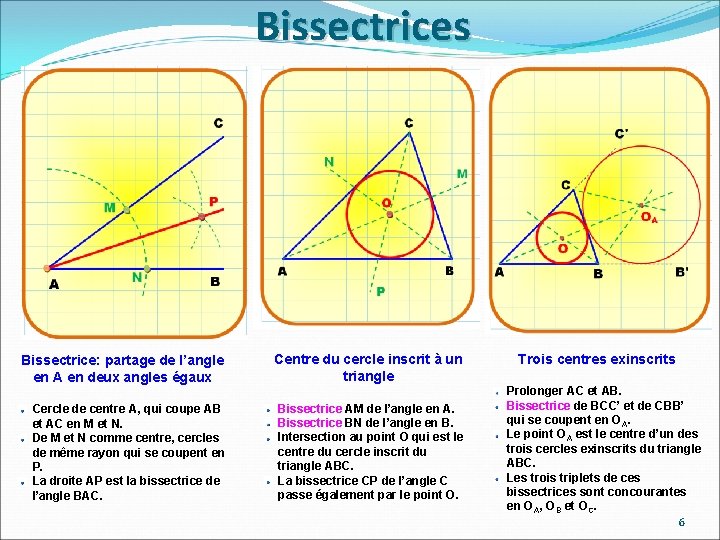
Bissectrices Bissectrice: partage de l’angle en A en deux angles égaux Centre du cercle inscrit à un triangle Cercle de centre A, qui coupe AB et AC en M et N. De M et N comme centre, cercles de même rayon qui se coupent en P. La droite AP est la bissectrice de l’angle BAC. Bissectrice AM de l’angle en A. Bissectrice BN de l’angle en B. Intersection au point O qui est le centre du cercle inscrit du triangle ABC. La bissectrice CP de l’angle C passe également par le point O. Trois centres exinscrits Prolonger AC et AB. Bissectrice de BCC’ et de CBB’ qui se coupent en O A. Le point OA est le centre d’un des trois cercles exinscrits du triangle ABC. Les trois triplets de ces bissectrices sont concourantes en OA, OB et OC. 6

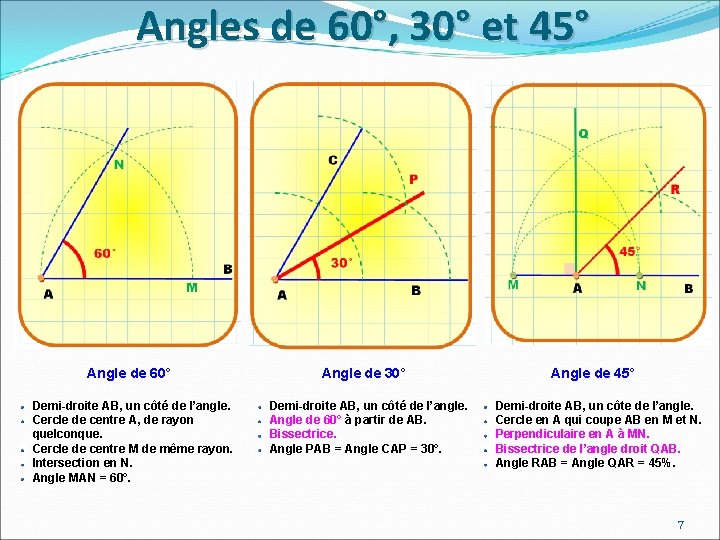
Angles de 60°, 30° et 45° Angle de 60° Demi-droite AB, un côté de l’angle. Cercle de centre A, de rayon quelconque. Cercle de centre M de même rayon. Intersection en N. Angle MAN = 60°. Angle de 30° Demi-droite AB, un côté de l’angle. Angle de 60° à partir de AB. Bissectrice. Angle PAB = Angle CAP = 30°. Angle de 45° Demi-droite AB, un côte de l’angle. Cercle en A qui coupe AB en M et N. Perpendiculaire en A à MN. Bissectrice de l’angle droit QAB. Angle RAB = Angle QAR = 45%. 7

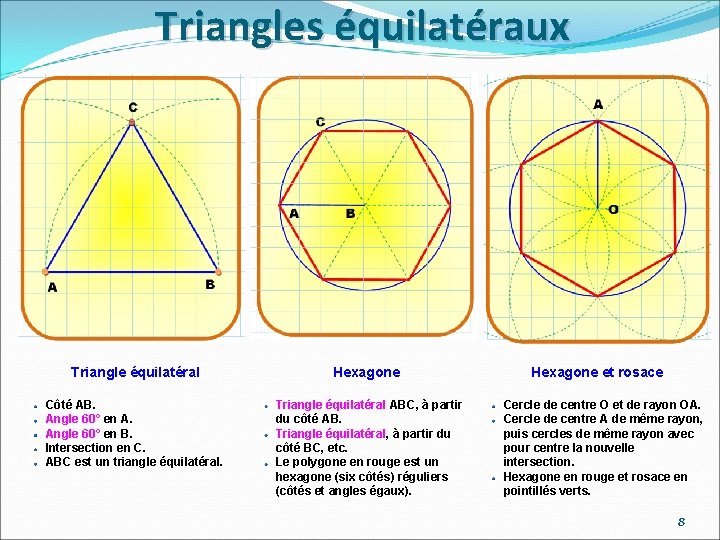
Triangles équilatéraux Triangle équilatéral Hexagone Côté AB. Angle 60° en A. Angle 60° en B. Intersection en C. ABC est un triangle équilatéral. Triangle équilatéral ABC, à partir du côté AB. Triangle équilatéral, à partir du côté BC, etc. Le polygone en rouge est un hexagone (six côtés) réguliers (côtés et angles égaux). Hexagone et rosace Cercle de centre O et de rayon OA. Cercle de centre A de même rayon, puis cercles de même rayon avec pour centre la nouvelle intersection. Hexagone en rouge et rosace en pointillés verts. 8

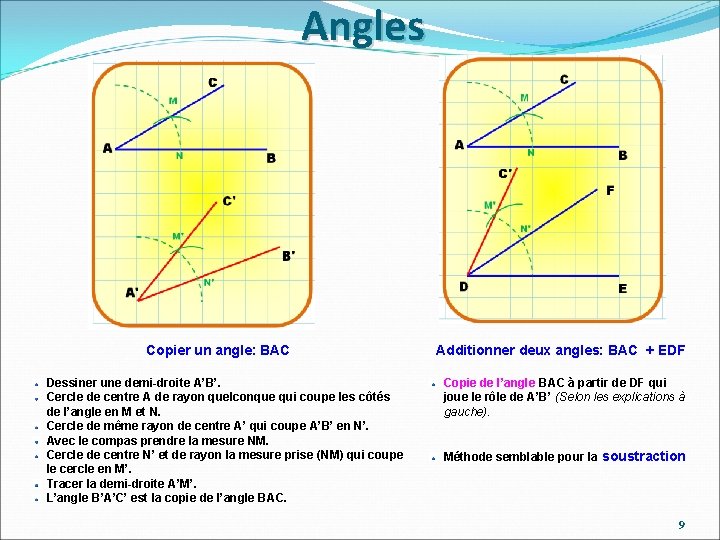
Angles Copier un angle: BAC Dessiner une demi-droite A’B’. Cercle de centre A de rayon quelconque qui coupe les côtés de l’angle en M et N. Cercle de même rayon de centre A’ qui coupe A’B’ en N’. Avec le compas prendre la mesure NM. Cercle de centre N’ et de rayon la mesure prise (NM) qui coupe le cercle en M’. Tracer la demi-droite A’M’. L’angle B’A’C’ est la copie de l’angle BAC. Additionner deux angles: BAC + EDF Copie de l’angle BAC à partir de DF qui joue le rôle de A’B’ (Selon les explications à gauche). Méthode semblable pour la soustraction 9

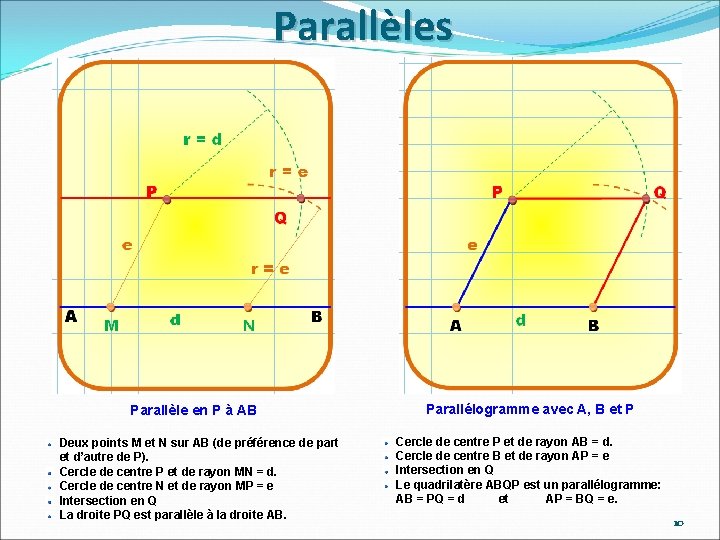
Parallèles Parallèle en P à AB Deux points M et N sur AB (de préférence de part et d’autre de P). Cercle de centre P et de rayon MN = d. Cercle de centre N et de rayon MP = e Intersection en Q La droite PQ est parallèle à la droite AB. Parallélogramme avec A, B et P Cercle de centre P et de rayon AB = d. Cercle de centre B et de rayon AP = e Intersection en Q Le quadrilatère ABQP est un parallélogramme: AB = PQ = d et AP = BQ = e. 10

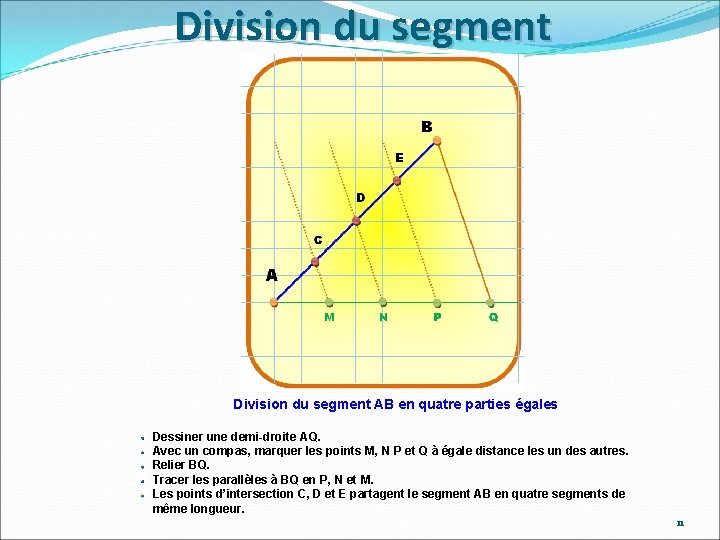
Division du segment AB en quatre parties égales Dessiner une demi-droite AQ. Avec un compas, marquer les points M, N P et Q à égale distance les un des autres. Relier BQ. Tracer les parallèles à BQ en P, N et M. Les points d’intersection C, D et E partagent le segment AB en quatre segments de même longueur. 11

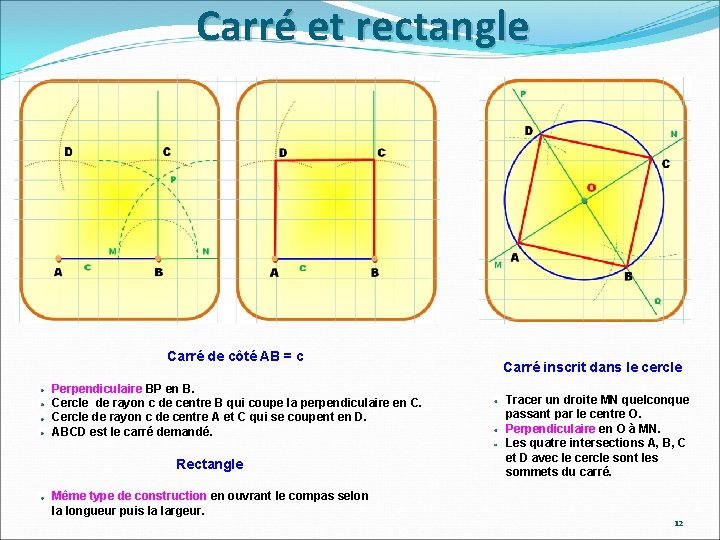
Carré et rectangle Carré de côté AB = c Perpendiculaire BP en B. Cercle de rayon c de centre B qui coupe la perpendiculaire en C. Cercle de rayon c de centre A et C qui se coupent en D. ABCD est le carré demandé. Rectangle Même type de construction en ouvrant le compas selon la longueur puis la largeur. Carré inscrit dans le cercle Tracer un droite MN quelconque passant par le centre O. Perpendiculaire en O à MN. Les quatre intersections A, B, C et D avec le cercle sont les sommets du carré. 12

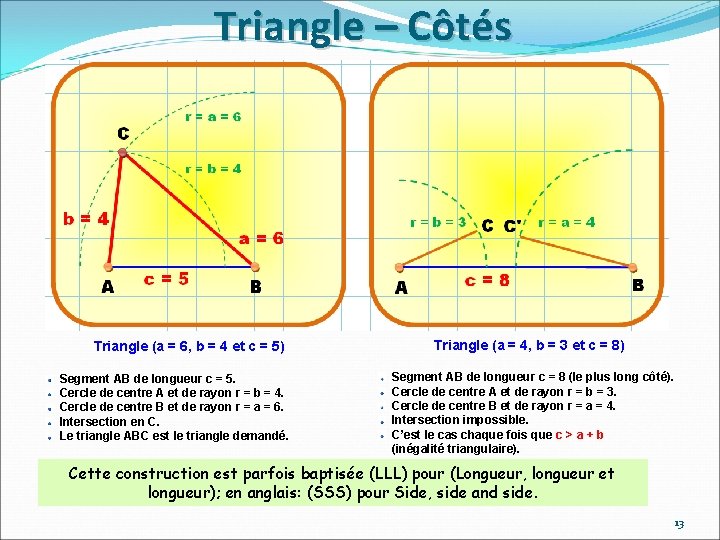
Triangle – Côtés Triangle (a = 6, b = 4 et c = 5) Segment AB de longueur c = 5. Cercle de centre A et de rayon r = b = 4. Cercle de centre B et de rayon r = a = 6. Intersection en C. Le triangle ABC est le triangle demandé. Triangle (a = 4, b = 3 et c = 8) Segment AB de longueur c = 8 (le plus long côté). Cercle de centre A et de rayon r = b = 3. Cercle de centre B et de rayon r = a = 4. Intersection impossible. C’est le cas chaque fois que c > a + b (inégalité triangulaire). Cette construction est parfois baptisée (LLL) pour (Longueur, longueur et longueur); en anglais: (SSS) pour Side, side and side. 13

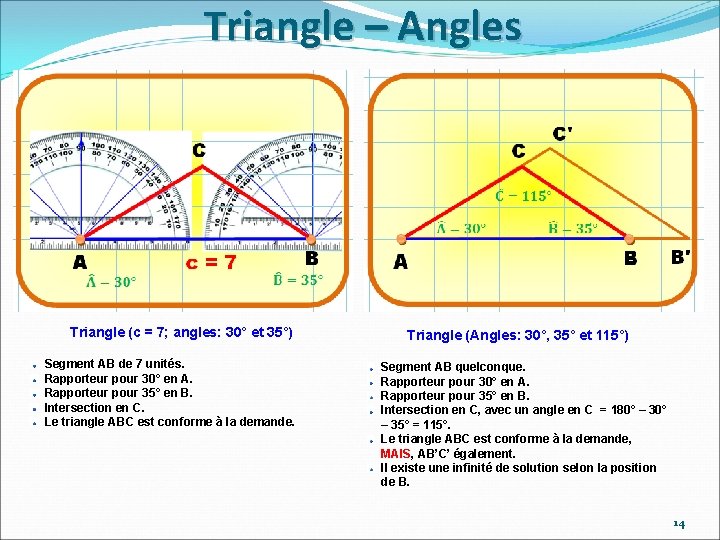
Triangle – Angles Triangle (c = 7; angles: 30° et 35°) Segment AB de 7 unités. Rapporteur pour 30° en A. Rapporteur pour 35° en B. Intersection en C. Le triangle ABC est conforme à la demande. Triangle (Angles: 30°, 35° et 115°) Segment AB quelconque. Rapporteur pour 30° en A. Rapporteur pour 35° en B. Intersection en C, avec un angle en C = 180° – 35° = 115°. Le triangle ABC est conforme à la demande, MAIS, AB’C’ également. Il existe une infinité de solution selon la position de B. 14

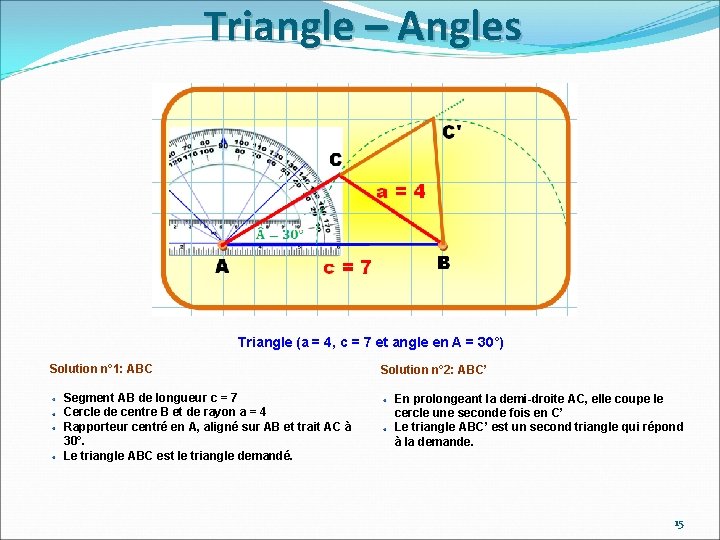
Triangle – Angles Triangle (a = 4, c = 7 et angle en A = 30°) Solution n° 1: ABC Segment AB de longueur c = 7 Cercle de centre B et de rayon a = 4 Rapporteur centré en A, aligné sur AB et trait AC à 30°. Le triangle ABC est le triangle demandé. Solution n° 2: ABC’ En prolongeant la demi-droite AC, elle coupe le cercle une seconde fois en C’ Le triangle ABC’ est un second triangle qui répond à la demande. 15

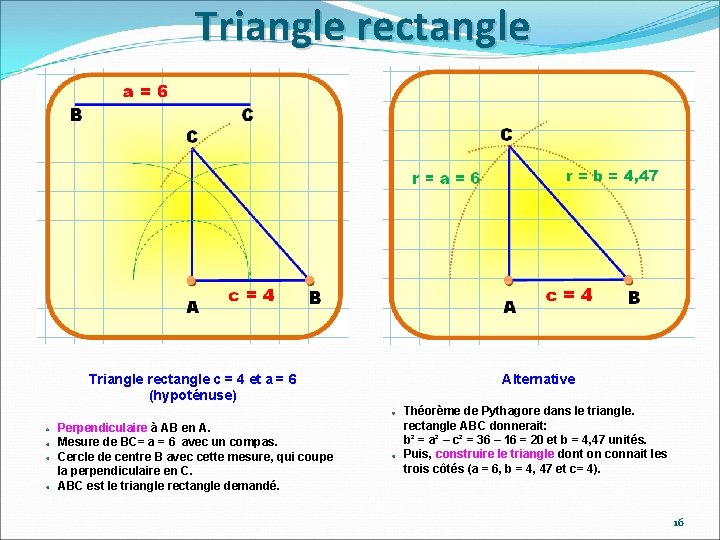
Triangle rectangle c = 4 et a = 6 (hypoténuse) Perpendiculaire à AB en A. Mesure de BC= a = 6 avec un compas. Cercle de centre B avec cette mesure, qui coupe la perpendiculaire en C. ABC est le triangle rectangle demandé. Alternative Théorème de Pythagore dans le triangle. rectangle ABC donnerait: b² = a² – c² = 36 – 16 = 20 et b = 4, 47 unités. Puis, construire le triangle dont on connait les trois côtés (a = 6, b = 4, 47 et c= 4). 16

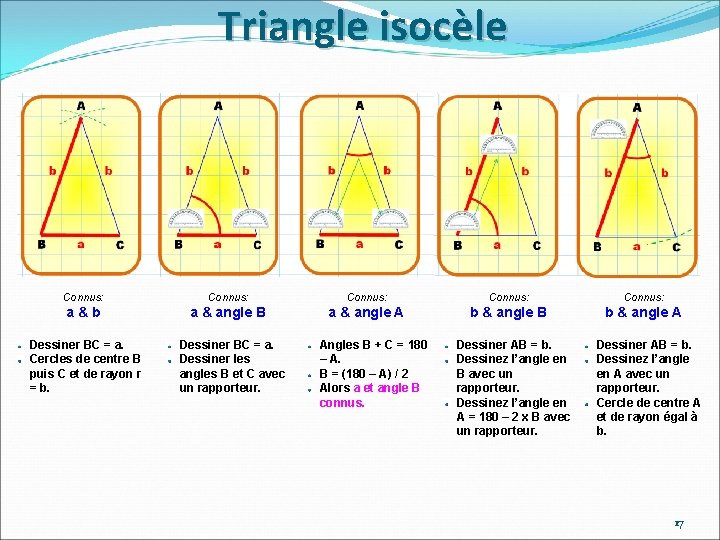
Triangle isocèle Connus: Connus: a&b a & angle B a & angle A b & angle B b & angle A Dessiner BC = a. Cercles de centre B puis C et de rayon r = b. Dessiner BC = a. Dessiner les angles B et C avec un rapporteur. Angles B + C = 180 – A. B = (180 – A) / 2 Alors a et angle B connus. Dessiner AB = b. Dessinez l’angle en B avec un rapporteur. Dessinez l’angle en A = 180 – 2 x B avec un rapporteur. Dessiner AB = b. Dessinez l’angle en A avec un rapporteur. Cercle de centre A et de rayon égal à b. 17

Triangle isocèle (a, A) Connus: a & angle en A (alternative) Avec un rapporteur dessiner l’angle BAC connu en A. Bissectrice AM de l’angle BAC. Perpendiculaire en N (quelconque) à AM. Porter la longueur a/2 de part et d’autre de N: NP = NQ = a/2. Perpendiculaires en P et Q à PQ. Les points d’intersection B et C sont les deux autres sommets du triangle isocèle demandé. 18

Centre du cercle (1) Un point M quelconque; deux droites MN et MP. Leur médiatrices (RO et QO) se coupent en O. Le point O est le centre du cercle bleu. Centre du cercle (2) Une droite coupe le cercle en M et N. Perpendiculaires MP et NQ à MN en M et N. Tracer MQ et PN qui se coupent en O. Le point O est le centre du cercle bleu. Les triangles rectangles MNP et MNQ sont inscrits dans le cercle. 19

Tangente au cercle Tangentes à partir du point P externe Tangente en A au cercle Cercle de centre O (bleu). Droite OA. Perpendiculaire PQ en A à OA. La droite PQ est la tangente en A au cercle initial. Cercle de centre O (bleu). Droite OP. Médiatrice RS de OP. Cercle de centre M et de rayon OM. Intersections avec le cercle en T et T’. Les droites PT et PT’ sont les deux tangentes au cercle. Explications (angles repérés par un nombre) Triangle isocèle MOT: 1 + 3 = 180°. Triangle isocèle MPT: 2 + 4 = 180°. Somme: 1 + 2 + 180° = 180° + 180° 1 + 2 = 90° => OTP est un angle droit. 20

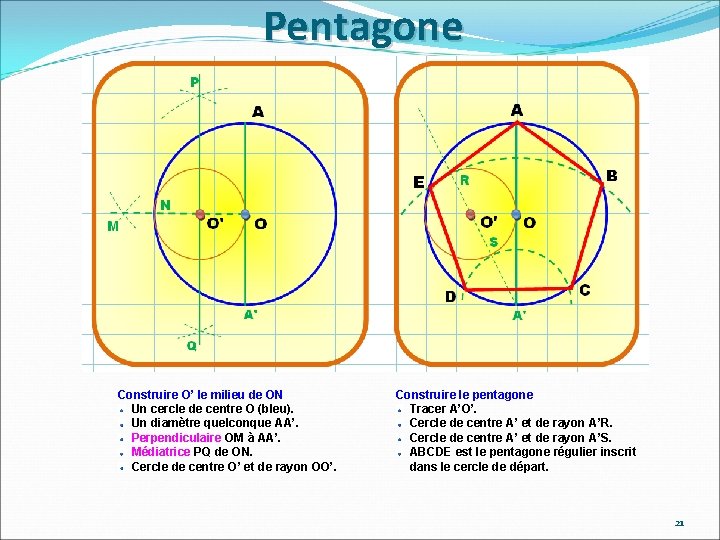
Pentagone Construire O’ le milieu de ON Un cercle de centre O (bleu). Un diamètre quelconque AA’. Perpendiculaire OM à AA’. Médiatrice PQ de ON. Cercle de centre O’ et de rayon OO’. Construire le pentagone Tracer A’O’. Cercle de centre A’ et de rayon A’R. Cercle de centre A’ et de rayon A’S. ABCDE est le pentagone régulier inscrit dans le cercle de départ. 21