Construction techniques in topological universal algebra Wolfram Bentz

Construction techniques in topological universal algebra Wolfram Bentz St. Francis Xavier University 2021/9/16 1

Introduction 2021/9/16 2

Universal Topological Algebra ● Algebra and Topology are compatible if all functions are continuous ● Via compatibility the algebraic structure restricts the topological one and vice versa ● General Question: How do algebraic properties correspond to topological ones? ● Typical Results have the form: The varieties with (A) are exactly those whose topological algebras satisfy (T) 2021/9/16 3

The construction task ● To draw topological conclusions from algebraic properties, one applies continuity “directly” to algebraic conditions ● No such direct way is apparent when trying to deduce algebraic conclusions from topological properties ● Hence, such results are proved by finding counterexamples 2021/9/16 4

The construction task ● Counterexamples for single varieties can show that a correspondence does not exist ● To get a more general result one needs to find a general construction principle, working for all varieties satisfying an algebraic property (a generic counterexample) 2021/9/16 5

Example ● Coleman (1997): A variety satisfies if and only if it is n-permutable for some n ● One direction already shown in Gumm (1984): n-permutable varieties satisfy 2021/9/16 6
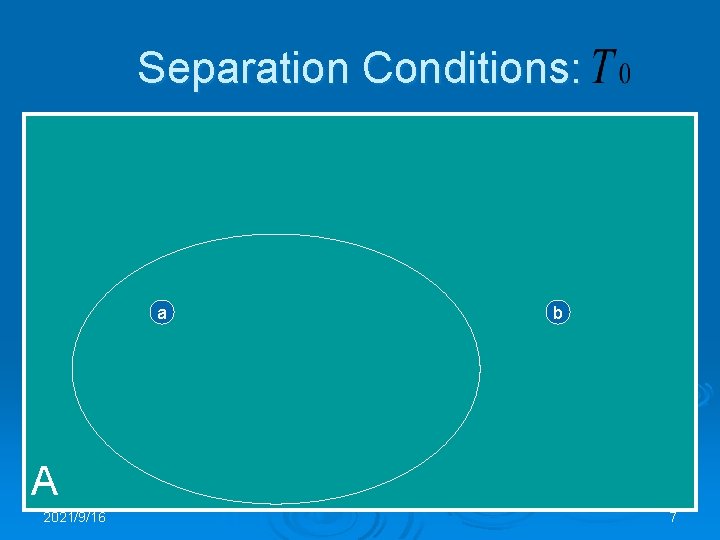
Separation Conditions: a b A 2021/9/16 7
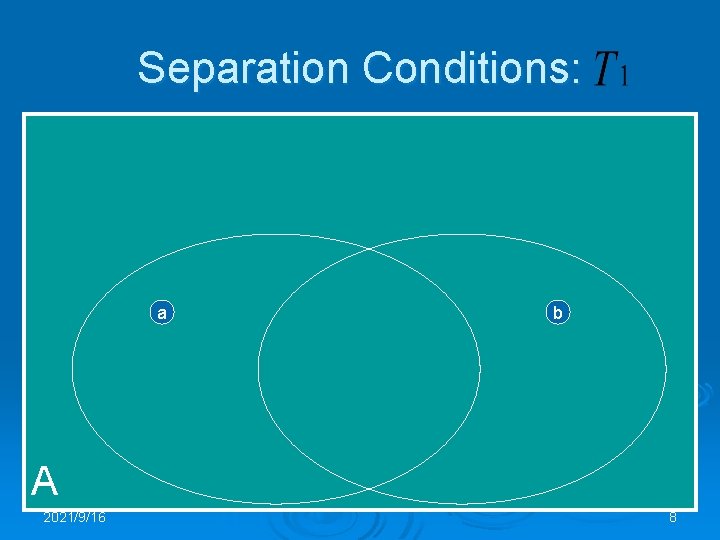
Separation Conditions: a b A 2021/9/16 8

Generic Counterexample ● Note: the original proof does not construct a counterexample directly; the following has been derived from it and various preceding results ● Let V be a variety that is not n-permutable for any n. ● Consider F(x, y), the free algebra in V over {x, y} 2021/9/16 9

Generic Counterexample ● For any element a in F(x, y) consider the elements b “reachable” from a by the following chain of equations, where the p’s are ternary term functions: a = p 1(x, y, y), p 1(x, x, y) = p 2(x, y, y), p 2(x, x, y) = p 3(x, y, y), …, pn-1(x, x, y) = pn-1(x, y, y), pn(x, x, y) = b 2021/9/16 10

Generic Counterexample ● a = p 1(x, y, y), p 1(x, x, y) = p 2(x, y, y), p 2(x, x, y) = p 3(x, y, y), …, pn-1(x, x, y) = pn-1(x, y, y), pn(x, x, y) = b ● Note that b = x is reachable from a = y (choose n = 1, p 1(u, v, w) = v), but if b = y would be reachable from a = x, then the p’s would be Hagemann-Mitschke terms. 2021/9/16 11

Generic Counterexample ● Now let a subset U of F(x, y) be open if for any element a in U, it also contains the elements reachable from a ● These sets form a compatible topology ● Every open set containing y must contain x. Conversely, the set of all elements reachable from x is open, but does not contain y 2021/9/16 12

Generic Counterexample ● So x and y are not separable in the T 1 sense. ● Identifying all elements that are contained in exactly the same open sets is a congruence ● The resulting quotient is T 0, but preserves the T 1 -inseparability between x and y 2021/9/16 13

More general examples ● The preceding construction relies heavily on the Hagemann – Mitschke terms for n-permutability ● This was possible because an exact algebraic characterization is known ● If this is not the case, look for a topological construction, that might not be compatible in general ● If it is “close” to a compatible construction, one can examine the cases were compatibility is achieved 2021/9/16 14

Swierczkowski – Extension ● A metric construction by Taylor (based on a topological one by Swieczkowski) ● Consider a space D with metric d, and the free algebra F over D (in a variety) ● For any two elements a and b of F, look at connections of the form a = p 1(x 1), p 1(y 1) = p 2(x 2), p 2(y 2) = p 3(x 3), …, pn-1(yn-1) = pn-1(xn-1), pn(yn) = b where the p’s are unary polynomial 2021/9/16 15

Swierczkowski – Extension ● For any two elements a and b of F, look at connections of the form a = p 1(x 1), p 1(y 1) = p 2(x 2), p 2(y 2) = p 3(x 3), …, pn-1(yn-1) = pn-1(xn-1), pn(yn) = b where the p’s are unary polynomial functions and the x’s and y’s are in D ● To each such connection assign the value Σd(xi, yi) ● Set d(a, b) to be the inf of all corresponding connection values, then d is a compatible 2021/9/16 16

Swierczkowski – Extension ● The Swierczkowski extension allows one to construct a topological algebra having a prescribed subspace, provided the subspace is metrizable 2021/9/16 17

Example ● When examining homotopy properties, Taylor used the free algebra over this space 2021/9/16 18

Swierczkowski – Extension ● If the desired counterexamples are not metrizable one can modify a Swierczkowski – Extension ● Coleman (1996): congruence permutable varieties do not necessarily satisfy 2021/9/16 19
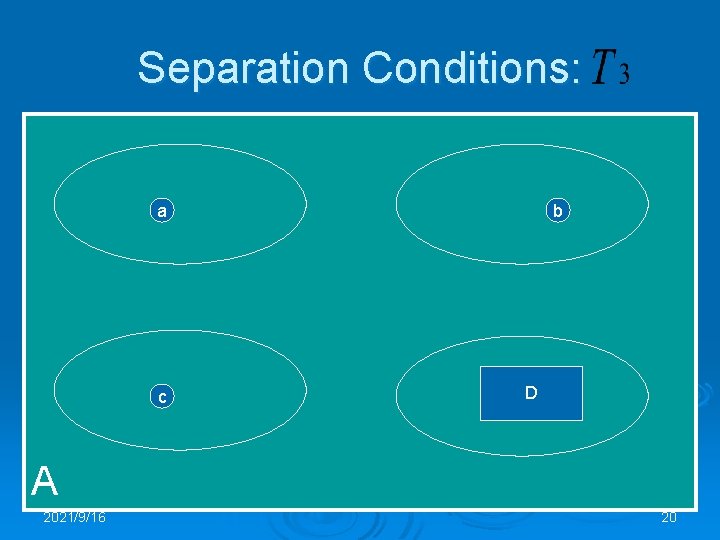
Separation Conditions: a c b D A 2021/9/16 20
Example 2021/9/16 21

Example (Coleman) ● Take the free algebra F over the real numbers ● Extend the metric topology of the reals to all of F (Swierczkowski) ● Enlarge the topology so that the subalgebra generated by Q is closed ● This topology satisfies T 1, but fails T 3 ● Examine whether continuity still holds in the new topology 2021/9/16 22

Example ● This construction works (as a topological space) for every non-trivial variety ● It appears likely that this is fundamental construction in the sense that it is a topological algebra in any variety failing 2021/9/16 23

Example ● Using this example, a large class of varieties was characterized ● Bentz (2007): A depth 1 variety V satisfies if and only if V is trivial ● Note: depth 1 is a restriction on the defining equations of a variety 2021/9/16 24
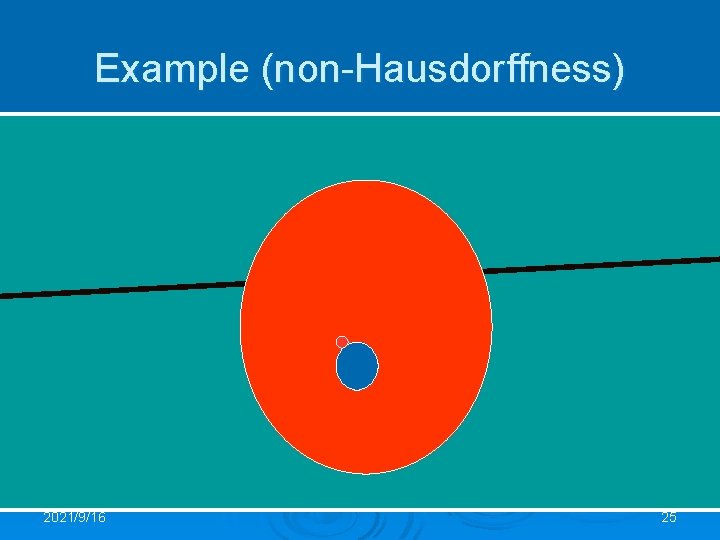
Example (non-Hausdorffness) 2021/9/16 25

Example of a partial construction (Coleman) ● Take the free algebra F over the real numbers ● Extend the metric topology of the reals to all of F (Swierczkowski) ● Introduce an extra point that is not Hausdorff-separable from some base point in F. ● Try to “fit” the algebraic structure 2021/9/16 26

Extending the algebra ● Involving the extra point in the operations must preserve the laws of the variety ● Everything must stay continuous with respect to the new topology 2021/9/16 27

Results with this construction ● Coleman: congruence 4 -permutability is not strong enough to force ● A Depth 1 variety satisfies if and only if it is congruence modular and n-permutable for some n (Bentz, 2006) ● This partial construction unfortunately will not work in all cases ● More doubled points might be a promising approach 2021/9/16 28

Thank you! Questions? 2021/9/16 29
- Slides: 29