Construction of Symmetry Coordinates for XY 2 bent

Construction of Symmetry Coordinates for XY 2 bent type molecules by Dr. D. UTHRA Head Department of Physics DG Vaishnav College Chennai-106

This presentation has been designed to serve as a self- study material for Postgraduate Physics students pursuing their programme under Indian Universities, especially University of Madras and its affiliated colleges. If this aids the teachers too who deal this subject, to make their lectures more interesting, the purpose is achieved. -D. Uthra

I acknowledge my sincere gratitude to my teacher Dr. S. Gunasekaran, for teaching me group theory with so much dedication and patience & for inspiring me and many of my friends to pursue research. - D. Uthra

Pre-requisites, before to you get on n n Knowledge of symmetry elements and symmetry operations Knowledge of various point groups Look-up of character tables Idea of the three dimensional structure of the molecule chosen

Normal modes of vibration of a molecule n n n 3 N-6 degrees of freedom are required to describe vibration of a non-linear molecule. 3 N-5 degrees of freedom are required to describe vibration of a linear molecule. Hence, n n For an XY 2 bent molecule N=3 ; 3 N-6 = 3 modes of vibration For an XY 3 pyramidal molecule N=4 ; 3 N-6 = 6 modes of vibration

Internal Coordinates n Changes in the bond lengths and in the inter-bond angles. Types of internal coordinates and their notation n n bond stretching (Δr ) angle deformation (ΔΦ) torsion (Δτ ) out of plane deformation (ΔΦ')

How to calculate number of vibrations using internal coordinates? nr = b n nΦ= 4 b-3 a+a 1 n nτ = b-a 1 n nΦ’= no. of linear subsections in a molecule where, b - no. of bonds (ignoring the type of bond) a - no. of atoms a 1 - no. of atoms with multiplicity one n Multiplicity means the number of bonds meeting the atom , ignoring the bond type. In H 2 O, multiplicity of H is 1 and that of O is 2. In NH 3, multiplicity of N is 3, while H is 1. In C 2 H 2, it is 1 for H and 2 for C (not 4 b’coz you ignore bond type). In CH 4, it is 1 for H and 4 for C. In CO 2, it is 2 for C and 1 for O.

Let us calculate the number of vibrations for a XY 2 bent molecule In XY 2 bent molecule, n b = 2 (no. of bonds) n a = 3 (no. of atoms) n a 1= 2 (no. of atoms with multiplicity one) Hence, n nr = 2 nΦ = 4*2 -3*3+2 =1 nτ = 2 -2 = 0 3 N-6 = nr+nΦ+nτ = 2+1= 3

Let us calculate the number of vibrations for a XY 3 bent molecule In XY 3 bent molecule, n b = 3 (no. of bonds) n a = 4 (no. of atoms) a 1= 3 (no. of atoms with multiplicity one) Hence, n n nr = 3 nΦ = 4*3 -3*4+3 =3 nτ = 3 -3 = 0 3 N-6 = nr+nΦ+nτ = 3+3=6

Symmetry Coordinates n n Symmetry coordinates describe the normal modes of vibration of the molecules They are the linear combinations of the internal coordinates related to various vibrations of the molecule

Basic properties of Symmetry Coordinates n n must be normalised must be orthogonal in the given species has the form Sj = ∑k Ujkrk not necessarily unique

How are Symmetry Coordinates formed? Generated by Projection operator method, S ij = ∑R χi(R)RLk R- symmetry operation of the point group χi(R)-character of the species (A 1, A 2, B 1, etc) covering the symmetry operation R (C 2, C 3, σ, etc) Lk-generating coordinate( may be single internal coordinate or some linear combination of internal coordinates) RLk-new coordinate which Lk becomes, after the symmetry operation is performed You are projecting the operator, that is doing symmetry operations on various internal coordinates of the chosen molecule, find what happens to those internal coordinates after projection and sum up the result!

To proceed further… n You need to have the knowledge of n n Structure of the chosen molecule Symmetry operations it undergoes Point group symmetry it belongs to Character table of that point group symmetry Caution : Brush up your knowledge and then proceed

Point Group and Symmetry Coordinates n n n Identify the point group symmetry of the molecule. By using its Character table, find the distribution of vibrations among its various species , ie find Γvib. Find symmetry coordinates defining each vibration ! Do you realise the importance of understanding symmetry operations and point groups and place the molecules correctly in their point group symmetry. If You are incorrect in finding the point group symmetry of the molecule, things will not turn out correctly!!
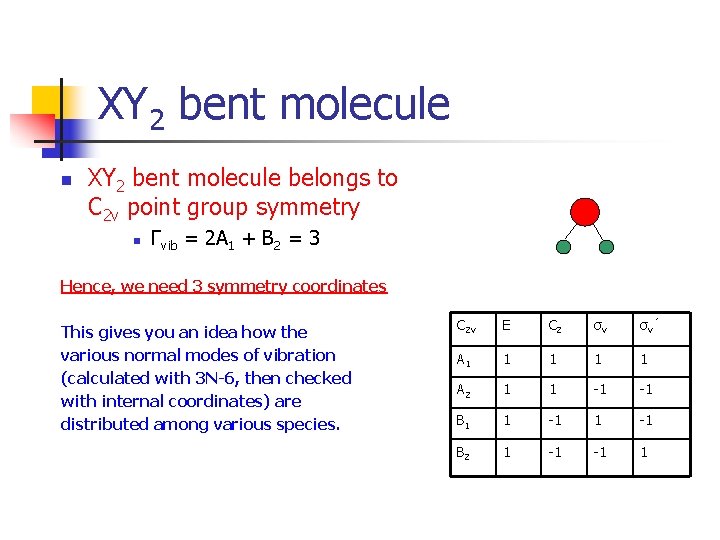
XY 2 bent molecule n XY 2 bent molecule belongs to C 2 v point group symmetry n Γvib = 2 A 1 + B 2 = 3 Hence, we need 3 symmetry coordinates This gives you an idea how the various normal modes of vibration (calculated with 3 N-6, then checked with internal coordinates) are distributed among various species. C 2 v E C 2 σv σv ’ A 1 1 1 A 2 1 1 -1 -1 B 1 1 -1 B 2 1 -1 -1 1

How to arrive at the symmetry coordinates? n As seen earlier, these are generated by Projection operator method, S ij = ∑R χi(R)RLk Step 1 : For every internal coordinate Lk, find RLk. Step 2 : Use character table and find the product χi(R)RLk for every R Step 3 : Sum them up Before that, keep a note of n n n internal coordinates of the chosen molecule what changes take place in them after every symmetry operation character table to which the molecule belongs to

S ij = ∑R χi(R)RLk In case of XY 2 bent molecule Internal coordinates (Lks) are Δd 1 , Δd Δd 1, Δα Symmetry operations (Rs) are E, C 2 , σv‘ and their respective χis are 1 or -1 (from character table ), while i = A 1, A 2, B 1, B 2 Γvib = 2 A 1 + B 2 = 3 In A 1 species S 1 = ? S 2 = ? In B 2 species S 3 = ? C 2 v E C 2 σv σv ’ A 1 1 1 A 2 1 1 -1 -1 B 1 1 -1 B 2 1 -1 -1 1
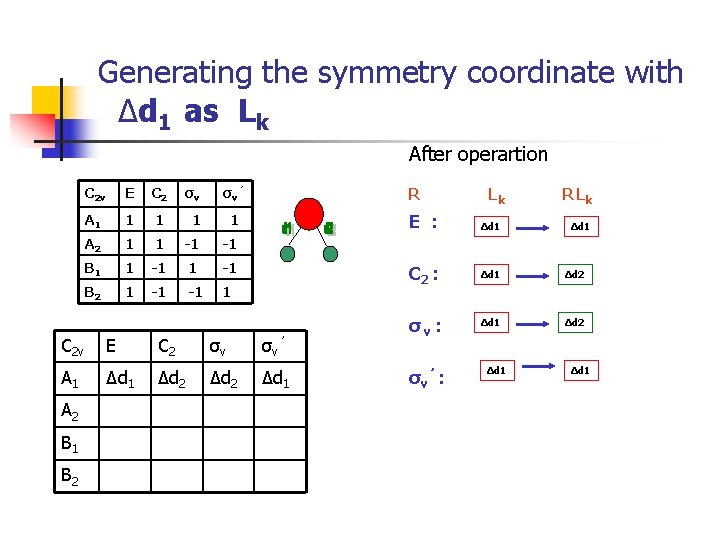
Generating the symmetry coordinate with Δd 1 as Lk After operartion C 2 v E C 2 σv σv ’ A 1 1 1 A 2 1 1 -1 -1 B 1 1 -1 B 2 1 -1 -1 1 R C 2 v E C 2 σv σv ’ A 1 Δd 2 Δd 1 A 2 B 1 B 2 Lk R Lk E : Δd 1 C 2 : Δd 1 Δd 2 σv ’ : Δd 1

S i = ∑R χi(R)RLk Now check your filled up table having χi(R)RLk entries C 2 v E C 2 σv A 1 A 2 B 1 Δd 2 Δd 1 Δd 2 -Δd 1 - Δd 2 -Δd 1 B 2 Δd 1 - Δd 2 -Δd 2 Find summation of the χi(R)RLk entries for every R σv ’ Sd 1 A 1= Δd 1+Δd 2+Δd 1 = 2(Δd 1+Δd 2) Sd 1 A 2= Δd 1+ Δd 2 - Δd 1 = 0 Sd 1 B 1= Δd 1 - Δd 2+ Δd 2 - Δd 1 = 0 Sd 1 B 2= Δd 1 - Δd 2+ Δd 1 = 2(Δd 1 -Δd 2) Δd 1 From above, you get Δd 1 § § SA 1 = Δd 1+Δd 2 SB 2 = Δd 1 - Δd 2

Generating the symmetry coordinate with Δd 2 as Lk Similarly generate the symmetry coordinates with Δd 2 as Lk § § C 2 v E C 2 σv σv ’ A 1 A 2 Δd 1 Δd 2 Δd 1 -Δd 2 B 1 Δd 2 -Δd 1 -Δd 2 B 2 Δd 2 -Δd 1 Δd 2 § § § S i = ∑R χi(R)RLk Sd 2 A 1=Δd +Δd +Δd =2(Δd +Δd ) Sd 2 A 2= Δd +Δd -Δd = 0 Sd 2 B 1= Δd -Δd +Δd -Δd = 0 Sd 2 B 2=Δd -Δd +Δd = 2(Δd –Δd ) 2 1 2 2 2 1 1 1 2 1 2 2 SA 1 = Δd 1+ Δd 2 SB 2 = Δd 2–Δd 1 =-(Δd 1 -Δd 2) 2 2 1 1

Generating the symmetry coordinate with Δα as Lk Now generate the symmetry coordinates with Δ α as Lk § A 1 A 2 Δα Δα C 2 σv σv ’ Δα Δα -Δα B 1 Δα -Δα B 2 Δα -Δα Δα = ∑R χi(R)RLk i § SαA 1 = 4 Δα SαA 2 = 0 SαB 1 = 0 SαB 2 = 0 § SA = Δα § C 2 v E S § § 1

SALCS- Symmetry Adapted Linear Combinations By projection operator method, employing S ij = ∑R χi(R)RLk SALCs for XY 2 bent molecule are found to be § § § SA 1 = Δd 1+Δd 2 SB 2 = Δd 1 - Δd 2 SA 1 = Δα

Condition to normalise and orthogonalise SALCs For normalisation n. For singly degenerate species, 2 ½ n. Uak = 1/q or Uak = ±(1/q) n. For doubly degenerate species, 2 2 n. Uak + Ubk = 2/q n. For triply degenerate species, 2 2 2 n. Uak + Ubk + Uck = 3/q q - total no. of symmetry equivalent internal coordinates involved in that SALC For orthogonalisation ∑k Uak. Ubk =0

For XY 2 bent molecule All three SALCs belong to singly degenerate species. Applying first condition, §In SA 1 = Δd 1+Δd 2 and SB 2 = Δd 1 - Δd 2, § q=2 §SA 1 = Δα § q=1
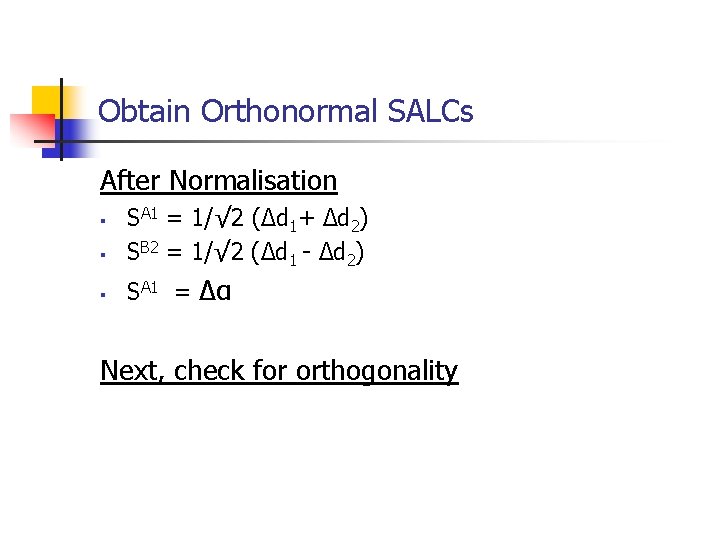
Obtain Orthonormal SALCs After Normalisation § SA 1 = 1/√ 2 (Δd 1+ Δd 2) SB 2 = 1/√ 2 (Δd 1 - Δd 2) § SA 1 = Δα § Next, check for orthogonality

Orthonormalised Symmetry Coordinates of XY 2 bent molecule § 3 N-6 = 3 distributed as Γvib. = 2 A 1 + B 2 = 3 § A 1 Species S 1 A 1 = 1/√ 2 (Δd 1+ Δd 2) § S 2 A 1 = § B 2 Species S 3 B 2 = 1/√ 2 (Δd 1 - Δd 2) Δα

Recap For an XY 2 bent molecule N=3 ; 3 N-6 = 3 modes of vibration n In XY 2 bent molecule, n b=2 n a=3 n a 1 = 2 Hence, n nr = 2 n nΦ = 4*2 -3*3+2 =1 n nτ = 2 -2 = 0 3 N-6 = 2 nr+1 nΦ = 3 n XY 2 bent molecule belongs to C 2 v point group symetry. Γvib. = 2 A 1 + B 2 = 3 In case of XY 2 bent molecule Lks are Δd 1 , Δd 2 , Δα Rs are E, C 2 , σv‘ and their respective χis are 1 or -1 (from character table ), while i = A 1, A 2, B 1, B 2 Γvib. = 2 A 1 + B 2 = 3 implies Check for orthogonality Normalisation A 1 Species S 1 = 1/√ 2 (Δd 1+ Δd 2) S 2 = Δα B 2 Species S 3 = 1/√ 2 (Δd 1 - Δd 2)

All the Best ! uthra mam Hope You enjoyed learning to form symmetry coordinates ! See U in the next session of group theory!
- Slides: 28