Construction of Aho Corasick automaton in Linear time

Construction of Aho Corasick automaton in Linear time for Integer Alphabets Shiri Dori & Gad M. Landau University of Haifa

Overview n Classic Aho Corasick n Our algorithm – Goto Function – Failure Function – Combining the two n Queries in O(m log|Σ|)

Set Pattern Matching Problem n Find patterns in text n P={P 1, P 2, . . . Pq}, in T n Aho and Corasick solved it in ’ 75 n Generalized version of KMP n Uses a state machine

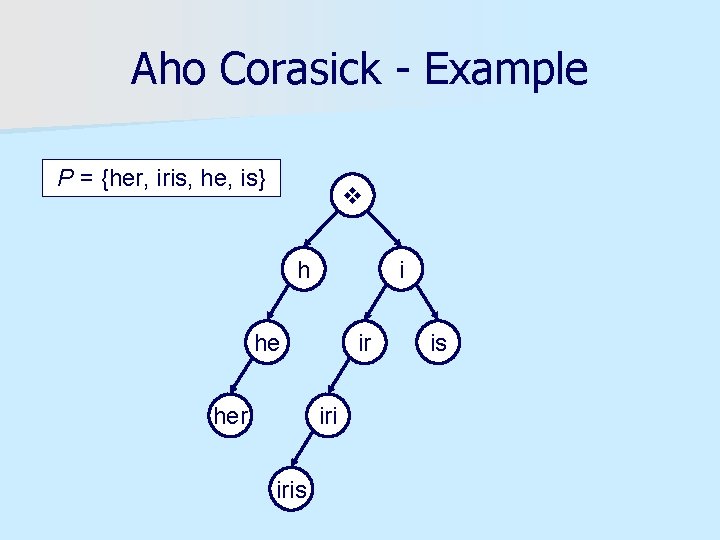
Aho Corasick - Example P = {her, iris, he, is} h i he her ir iris is

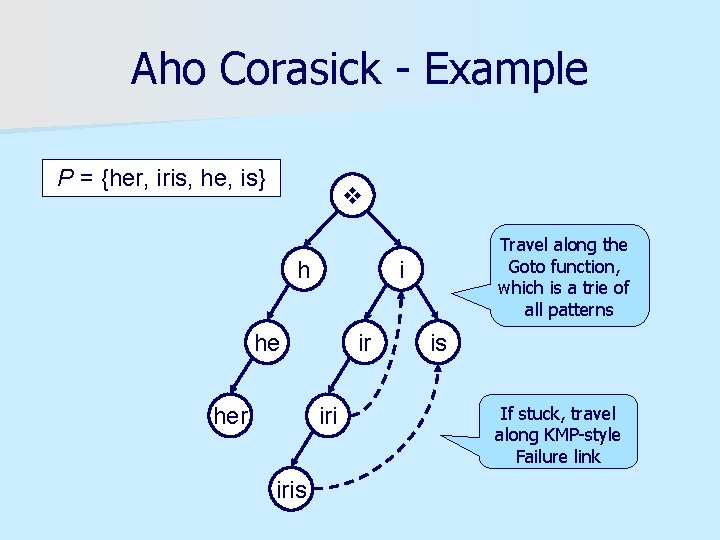
Aho Corasick - Example P = {her, iris, he, is} h i he her ir iris Travel along the Goto function, which is a trie of all patterns is If stuck, travel along KMP-style Failure link

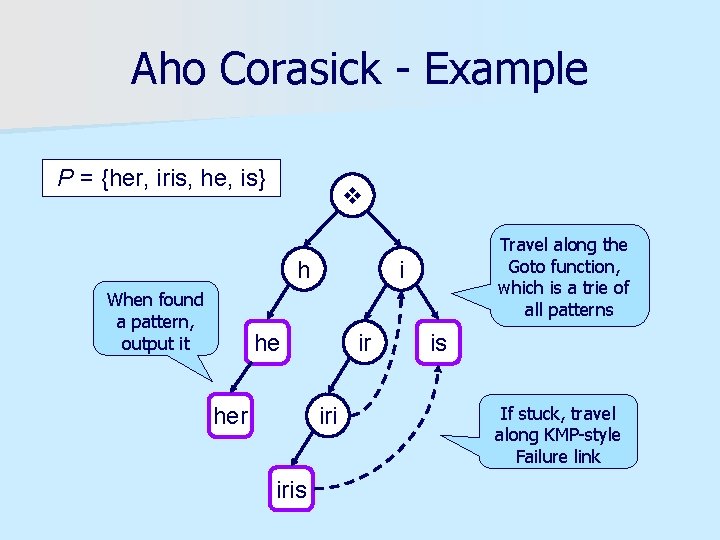
Aho Corasick - Example P = {her, iris, he, is} h When found a pattern, output it i he her ir iris Travel along the Goto function, which is a trie of all patterns is If stuck, travel along KMP-style Failure link

Aho Corasick Definitions n Goto function: a trie of the patterns n Failure function: for each label, the largest suffix which is a prefix of a pattern – KMP, but prefix of any pattern qualifies n Output function: patterns ending at this label

Classic Aho Corasick – Analysis n Constructed in O(n) (cumulative pattern length) n Answered queries in O(m + k) n. . . For constant alphabets only! n For integer alphabets, Σ=O(nc), algorithm changes depending on branching method – List, Array or Search Tree n Recent developments inspire for better! – Farach-97; Karkkäinen & Sanders-03; – Ko & Aluru-03; Kim, Sim, Park & Park-03

Our Results n Our algorithm achieves better results: n Construction in O(n) time, O(n) space n Query in O(m log|Σ|) n Works for integer alphabets, Σ = O(nc)

Algorithm: Goto Function n Sort patterns in time linear to their length – By building suffix array of Sp=$P 1$P 2$. . . $Pq$, and just ignoring non-pattern suffixes – Or by two-pass radix sort, O(D + Σ) = O(n) § Paige & Tarjan, ’ 87; Andersson & Nilsson, ‘ 94 n Now create the trie in lexicographic order n Hold a list of sons; insert each new node to the end of the list

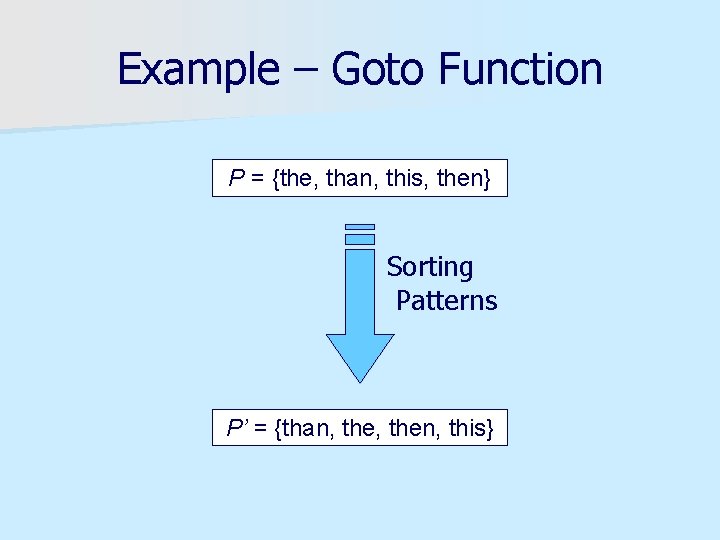
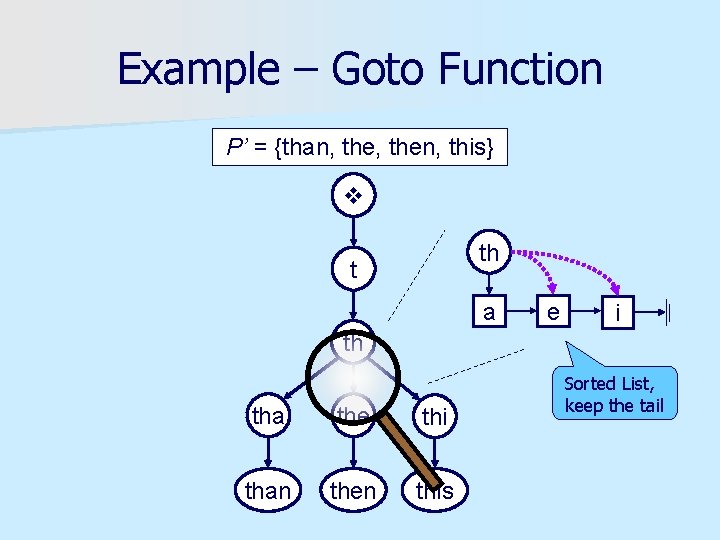
Example – Goto Function P = {the, than, this, then} Sorting Patterns P’ = {than, then, this}

Example – Goto Function P’ = {than, then, this} than, the then, then this t th tha the thi than then this

Example – Goto Function P’ = {than, then, this} th t a e i th tha the thi than then this Sorted List, keep the tail

Algorithm: Failure Function n We need to construct Failure links on trie n Original algorithm included traversing trie n We found a deep connection between: – Failure function of the patterns, and – Suffix Tree of the reversed patterns § Or Enhanced Suffix Array § Abouelhoda, Kurtz & Ohlebusch-04; Kim, Jeon & Park-04 n We’ll “learn by example”. . .

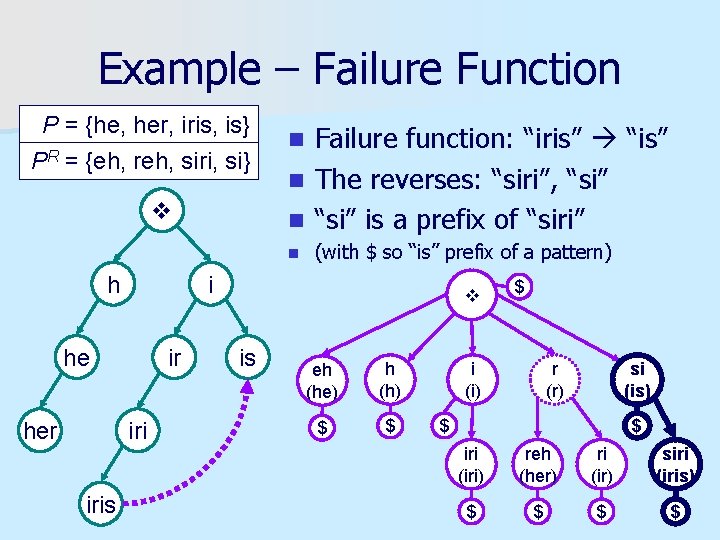
Example – Failure Function P = {he, her, iris, is} PR = {eh, reh, siri, si} Failure function: “iris” “is” n The reverses: “siri”, “si” n “si” is a prefix of “siri” n n h i he her ir iris (with $ so “is” prefix of a pattern) is eh (he) h (h) $ $ $ i (i) r (r) si (is) $ $ iri (iri) reh (her) ri (ir) siri (iris) $ $

Understanding Failure Function n Failure function is defined as: largest suffix, which is a prefix of any pattern n Reverse: “largest suffix” “largest prefix” – Any prefix of a label will be its ancestor in ST – Largest means nearest n “prefix of pattern” “suffix of pattern” – It will be a node in the ST, marked by a $ n So: closest ancestor which is marked by $

Algorithm: Failure Function n We found a deep connection between: – Failure function of the patterns, and – Suffix Tree of the reversed patterns n We define Sp=$P 1$P 2$. . . $Pq$ n We define TR to be the suffix tree of (Sp)R n TR can be built in linear time – Can use Enhanced Suffix Array, ER, instead – Note: TR is a Generalized Suffix Tree n How will we link the trie and TR?

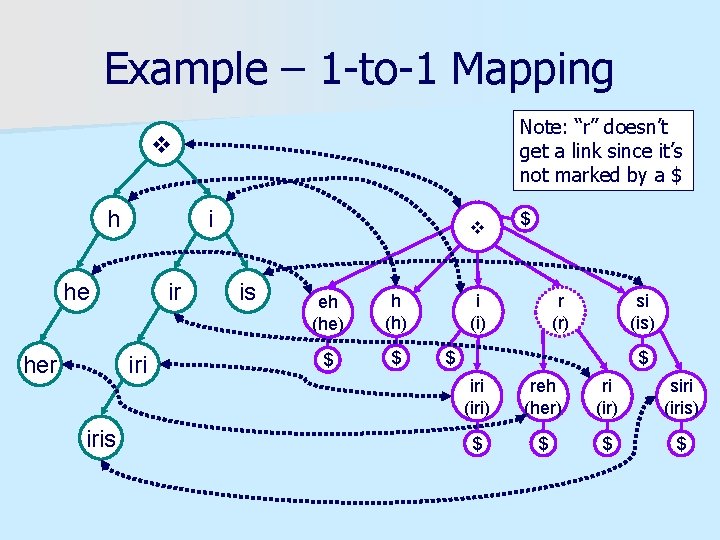
Example – 1 -to-1 Mapping Note: “r” doesn’t get a link since it’s not marked by a $ h i he her ir iris is eh (he) h (h) $ $ $ i (i) r (r) si (is) $ $ iri (iri) reh (her) ri (ir) siri (iris) $ $

Example – 1 -to-1 Mapping h i he her ir iris is eh (he) h (h) $ $ $ i (i) r (r) si (is) $ $ iri (iri) reh (her) ri (ir) siri (iris) $ $

Algorithm: Review n Build Goto function (trie) – Sort patterns – Construct trie n Build Failure function – Construct TR – Compute proper ancestor for $-marked nodes n Combine information – Through mapping, create Failure links on trie

Adjustment for Integer Alphabet n We used recent developments (SA, ST) n Constructed Goto: using suffix array n Found a connection between Failure function and suffix trees n Thus, reduced the construction to O(n) n Yet, manage to keep queries at O(m log|Σ|) n Again - how?

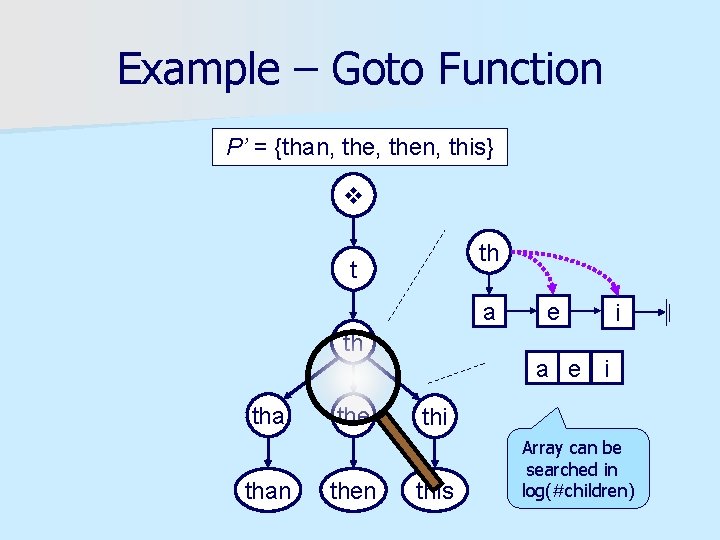
Queries in O(m log|Σ|) n We’ve built the trie in O(n) – But we have a sorted list – Search is compromised n Our simple solution…

Example – Goto Function P’ = {than, then, this} th t a th than then e i a e i this Array can be searched in log(#children)

Queries in O(m log|Σ|) n Once the trie is complete – Convert lists in each node to arrays – Array’s size is known; O(n) space overall – Binary search can now be employed n Reduce the time spent in each node to log(# children) = O(log|Σ|) n Can be applied to Suffix Tree built from Suffix Array + LCP

The End Thanks!

Algorithm: Combining the two n Build a 1 -to-1 mapping between $-marked nodes in TR and trie nodes n We compute mapping through the string: – For each char in Sp, we keep its Goto node – For each suffix tree node, we know what indices it represents (in (Sp)R, and so in Sp) n Now, build Failure links atop the trie – Like we saw in the example

Algorithm: Failure Function n For each node, find its “proper ancestor” – Closest ancestor marked with a $ – Found with a simple preorder traversal n The properties of TR ensure that. . . – For each failure link v 1 v 2 – And their corresponding nodes, u 1 and u 2 – u 2 = proper ancestor of u 1 n If we link trie and TR, we find the Failure! n How will we link them?

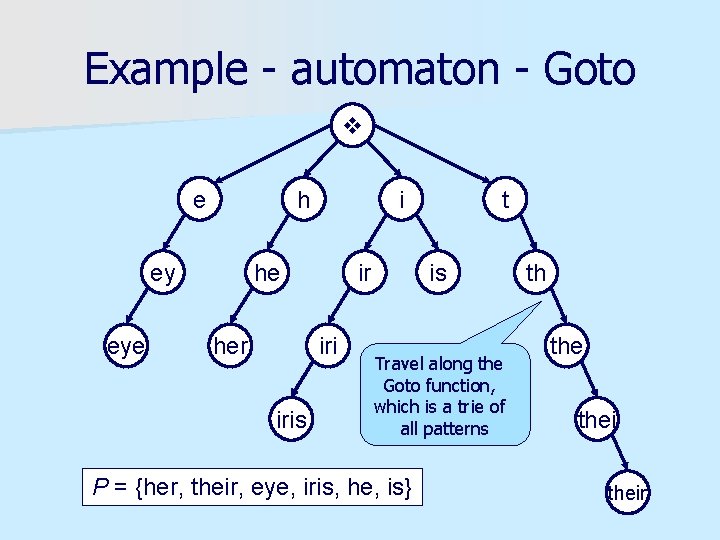
Example - automaton - Goto e h ey eye i he her ir iris t is Travel along the Goto function, which is a trie of all patterns P = {her, their, eye, iris, he, is} th their

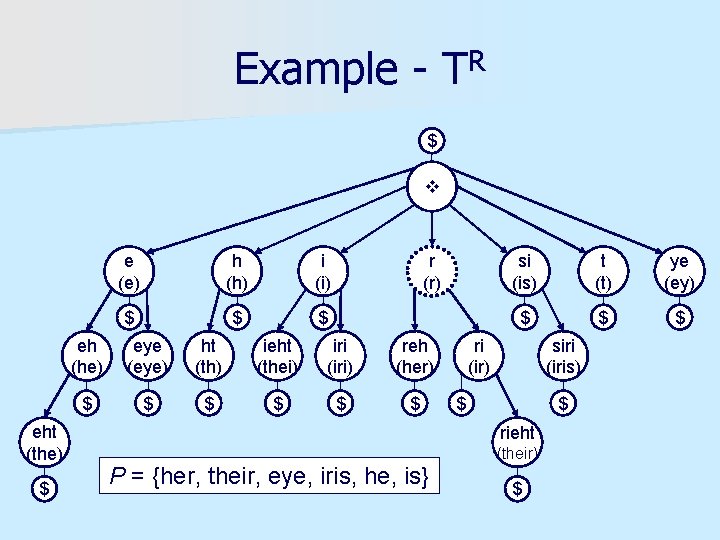
Example - TR $ eht (the) $ e (e) h (h) i (i) $ $ $ r (r) eh (he) eye (eye) ht (th) ieht (thei) iri (iri) reh (her) $ $ $ si (is) t (t) ye (ey) $ $ $ ri (ir) siri (iris) $ $ rieht (their) P = {her, their, eye, iris, he, is} $

Example - TR and Failure e h ey P = {her, their, eye, iris, he, is} i ir he eye t is th iri her $ thei iris e (e) h (h) i (i) $ $ r (r) eh (he) $ eye (eye) ht (th) ieht (thei) iri (iri) reh (her) $ $ $ si (is) t (t) ye (ey) $ $ $ ri (ir) siri (iris) $ $ eht (the) (their) $ $ rieht their iris is the e eye e their ir

TR - Reversed Suffix Tree n We defined Sp=$P 1$P 2$. . . $Pq$ n We define TR to be the suffix tree of (Sp)R n This tree has interesting properties: – Each trie node v is represented by exactly one TR node u, so that Label(v) = Label(u)R – In TR, a node’s label is a prefix of its child’s label; in the trie, it is a suffix of the original – A $-marked node in TR means that the original label is a prefix of a pattern

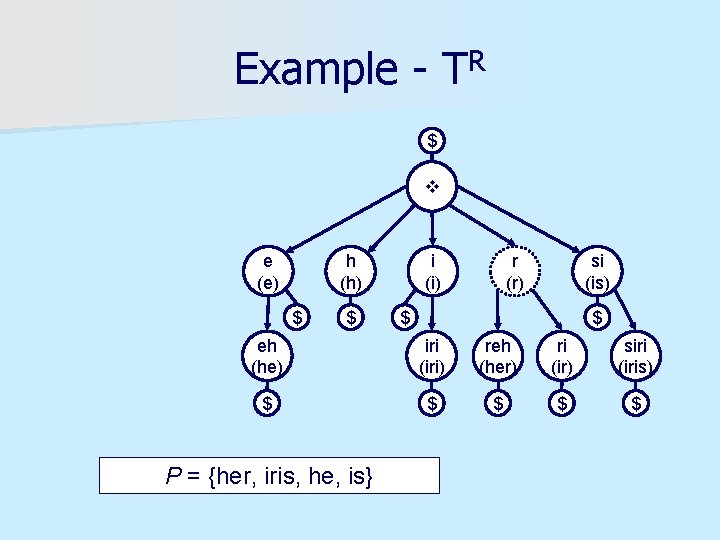
Example - TR $ e (e) h (h) $ $ i (i) r (r) si (is) $ $ eh (he) iri (iri) reh (her) ri (ir) siri (iris) $ $ $ P = {her, iris, he, is}

Example - TR and Failure n We took: P = {her, their, eye, iris, he, is} n Failure of “their” “ir” (from “iris”) – Largest suffix, which is a prefix of a pattern n Their reverse strings are “rieht”, “ri” – Now prefix. . . its ancestor in a suffix tree! n To be a prefix of a pattern px, should be a suffix of the reverse pattern (px)R – So it will be in suffix tree, and end with a $