Construction of a relativistic field theory Lagrangian Nonrelativistic

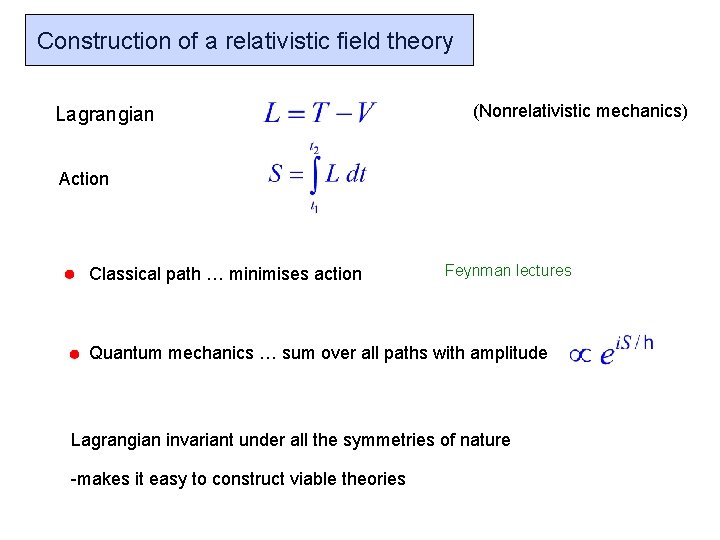
Construction of a relativistic field theory Lagrangian (Nonrelativistic mechanics) Action Classical path … minimises action Feynman lectures Quantum mechanics … sum over all paths with amplitude Lagrangian invariant under all the symmetries of nature -makes it easy to construct viable theories

Lagrangian formulation of the Klein Gordon equation Klein Gordon field Manifestly Lorentz invariant } } T V Classical path : Dimensions? Euler Lagrange equation

Euler Lagrange equs Principle of least action : 0 (surface integral) Euler Lagrange equation

Lagrangian formulation of the Klein Gordon equation Klein Gordon field Manifestly Lorentz invariant } } T V Euler Lagrange equation Klein Gordon equation

The Lagrangian and Feynman rules Associate with the various terms in the Lagrangian a set of propagators and vertex factors The propagators determined by terms quadratic in the fields, using the Euler Lagrange equations. The remaining terms in the Lagrangian are associated with interaction vertices. The Feynman vertex factor is just given by the coefficient of the corresponding term in }

New symmetries Is invariant under …an Abelian (U(1)) gauge symmetry A symmetry implies a conserved current and charge. e. g. Translation Rotation Momentum conservation Angular momentum conservation What conservation law does the U(1) invariance imply?

Noether current Is invariant under …an Abelian (U(1)) gauge symmetry 0 (Euler lagrange eqs. ) Noether current

The Klein Gordon current Is invariant under …an Abelian (U(1)) gauge symmetry This is of the form of the electromagnetic current we used for the KG field

The Klein Gordon current Is invariant under …an Abelian (U(1)) gauge symmetry This is of the form of the electromagnetic current we used for the KG field is the associated conserved charge

Suppose we have two fields with different U(1) charges : . . no cross terms possible (corresponding to charge conservation)

U(1) local gauge invariance and QED not invariant due to derivatives To obtain invariant Lagrangian look for a modified derivative transforming covariantly Need to introduce a new vector field

is invariant under local U(1) Note : is equivalent to universal coupling of electromagnetism follows from local gauge invariance

The electromagnetic Lagrangian Forbidden by gauge invariance The Euler-Lagrange equations give Maxwell equations ! `

The photon propagator The propagators determined by terms quadratic in the fields, using the Euler Lagrange equations. Gauge ambiguity i. e. with suitable “gauge” choice of α (“ξ” gauge) want to solve In momentum space (‘t Hooft Feynman gauge ξ=1)

The inclusion of fermions Weyl spinors Dirac spinor 2 -component spinors of SU(2) Rotations and Boosts Dirac Gamma matrices Weyl basis

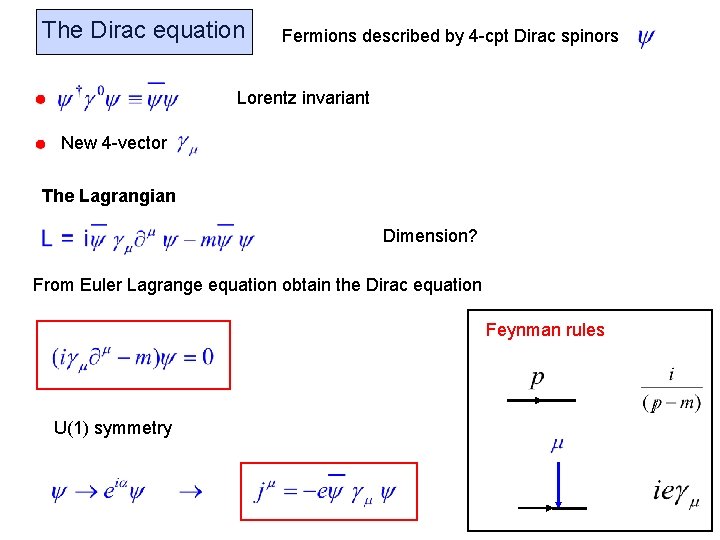
The Dirac equation Fermions described by 4 -cpt Dirac spinors Lorentz invariant New 4 -vector The Lagrangian Dimension? From Euler Lagrange equation obtain the Dirac equation Feynman rules U(1) symmetry