Constructing Signature Graphs for Signature Files Dr Yangjun

Constructing Signature Graphs for Signature Files Dr. Yangjun Chen Dept. Applied Computer Science University of Winnipeg Canada

• Motivation • Signature Files as Indexes • Signature Graph and its Construction – Searching a Signature Graph • Maintenance of Signature Graph • Summary and Future Work

Motivation • Establish Indexes to speed up query evaluation • B+-trees, inverted files, signature files • Signature files: simple and easy for maintenance • Signature graphs: less time for searching

Signature Files as Indexes § Definition A signature for a key word or an attribute value is hash-coded bit string. § Signature construction - Important parameters: m: number of 1 s in bit string F: length of bit string D: size of a block (or average number of the key words of an element) - optimal choice of the parameters: F ln 2 = m D.

• Example: (constructing a signature for a word with m = 4 and F = 12) “database” letter triplets: dat, ata, tab, aba, bas, ase H(dat) = 5, H(ata) = 1, H(tab) = 8, H(aba) = 1, H(bas) = 10, H(ase) = 8. 100 010 100

Signature Files as Indexes text: … SGML … database …information … matching word signatures: query signatures: results 010000100110 match with SGML queries: 010000100110 SGML OS database 100010010100 XML 011000100100 no match with OS information 010100011000 informatik 110100100000 object signature 110110111110 (OS) false drop

Example: relation: name sex John male . . . query: John Ù male . . . query signature: 1010 0101

Signature Graph Consider a signature si of length m. We denote it as si = si[1]si[2]. . . si[m], where each si[j] {0, 1} (j = 1, . . . , F). We also use si(j 1, . . . , jh) to denote a sequence of pairs w. r. t. si: (j 1, si[j 1])(j 2, si[j 2]). . . (jh, si[jh]), where 1 jk m for k {1, . . . , h}. Definition (signature identifier) Let S = s 1. s 2. . sn denote a signature file. Consider si (1 i n). If there exists a sequence: j 1, . . . , jh such that for any k i (1 k n) we have si(j 1, . . . , jh) sk(j 1, . . . , jh), then we say si(j 1, . . . , jh) identifies the signature si or say si(j 1, . . . , jh) is an identifier of si.

Example: s 8(5, 1, 4) = (5, 1)(1, 1)(4, 0) (*For any i 8 we have si(5, 1, 4) s 8(5, 1, 4). For instance, s 5(5, 1, 4) = (5, 0)(1, 0)(4, 1) s 8(5, 1, 4), s 2(5, 1, 4) = (5, 1)(1, 1)(4, 1) s 8(5, 1, 4), and so on. *) s 1(5, 4, 1) = (5, 0)(4, 1)(1, 1) (*For any i 1 we have si(5, 4, 1) s 1(5, 4, 1). *)

Signature Graph • Definition (signature graph) A signature graph G for a signature file S = s 1. s 2. . sn, where si sj for i j and |sk| = F for k = 1, . . . , n, is a graph G = (V, E) such that 1. each node v V is of the form (p, skip), where p is a pointer to a signature s in S, and skip is a non-negative integer i. If i > 0, it tells that the ith bit of sq will be checked when searching. If i = 0, s will be compared with sq. 2. Let e = (u, v) E. Then, e is labeled with 0 or 1 and skip(u) > 0. Let skip(u) = i. If e is labeled with 0 and i > 0, the ith bit of the signature pointed to by p(v) is 0. If e is labeled with 1 and i > 0, the ith bit of the signature pointed to by p(v) is 1. A node v with skip(u) = 0 does not have any children.

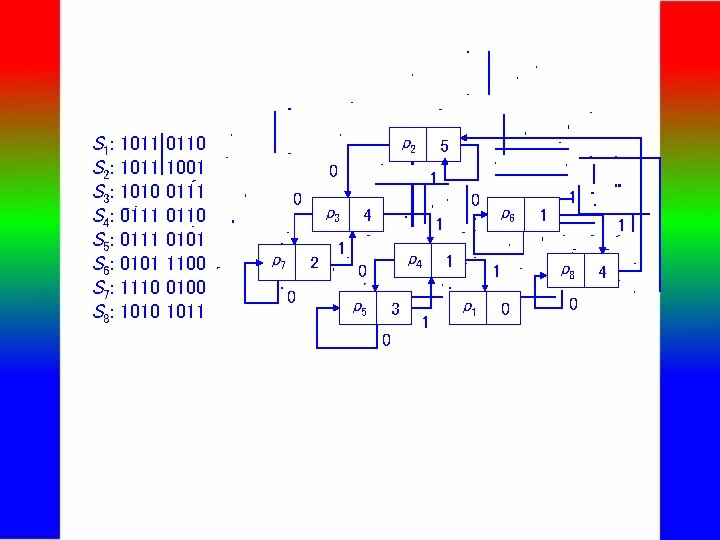
S 1: 1011 0110 S 2: 1011 1001 S 3: 1010 0111 S 4: 0111 0110 S 5: 0111 0101 S 6: 0101 1100 S 7: 1110 0100 S 8: 1010 1011 p 2 5 0 0 p 7 p 3 2 0 1 0 4 1 1 p 4 0 p 5 3 0 1 1 p 6 1 p 1 0 1 1 1 p 8 0 4

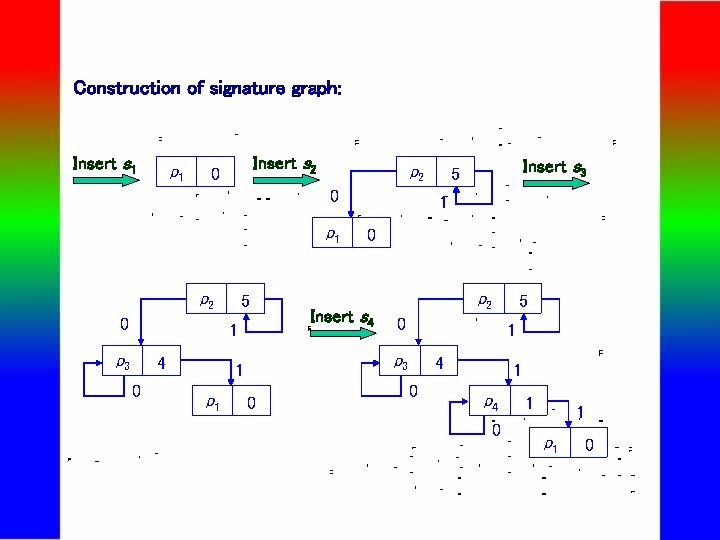
Construction of signature graph: Insert s 1 p 1 Insert s 2 0 p 1 p 2 0 5 1 p 3 4 0 p 1 1 0 Insert s 4 p 2 0 5 0 1 p 3 1 Insert s 3 5 4 0 1 p 4 0 1 1 p 1 0

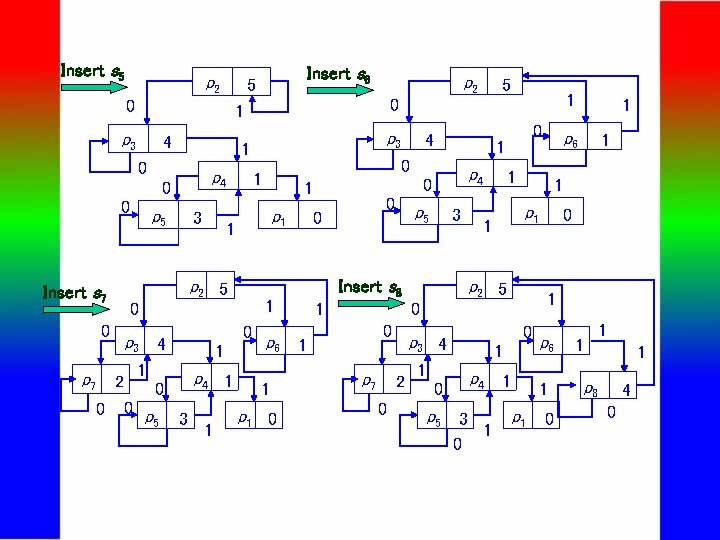
Insert s 5 p 2 0 4 p 4 0 0 p 7 3 1 0 1 1 p 4 1 0 3 1 1 0 0 p 1 0 3 Insert s 8 0 p 2 5 p 7 2 0 1 1 p 4 1 0 p 5 3 0 1 0 p 3 4 1 1 p 1 1 1 p 6 1 0 p 6 1 1 p 4 p 5 1 0 1 1 p 3 4 4 0 p 1 0 0 p 5 p 3 1 p 2 5 2 0 p 5 5 0 1 0 0 p 2 1 p 3 Insert s 7 Insert s 6 5 p 6 1 p 1 0 1 1 1 p 8 4 0

Signature Graph Searching a signature graph Denote sq(i) the i-th position of sq. During the traversal of a signature graph, the inexact matching can be done as follows: (i) Let v be the node encountered and sq (i) be the position to be checked. (ii) If sq (i) = 1, we move to the right child of v (iii)If sq (i) = 0, both the right and left child of v will be visited. (iv)A search along a path stops when a node without any child node or a node is encountered for the second time.

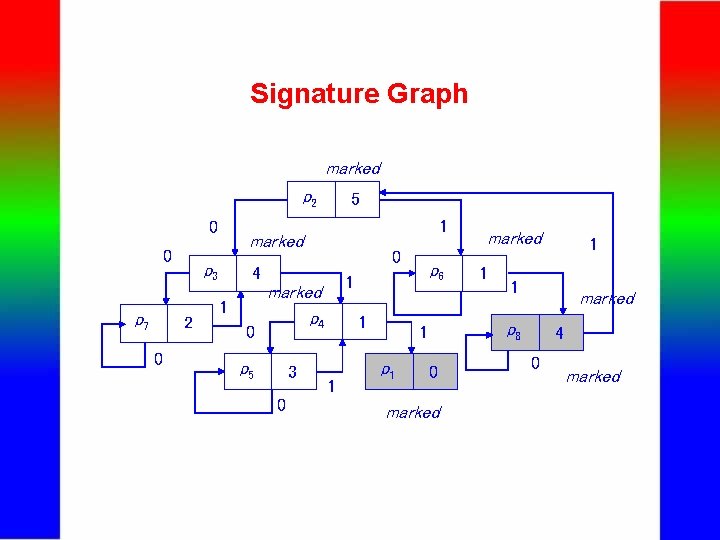
Signature Graph marked p 2 0 0 p 7 0 1 marked p 3 2 5 0 4 1 0 1 marked p 4 p 5 3 0 p 6 1 1 1 0 marked 1 1 marked p 8 1 p 1 marked 4 0 marked

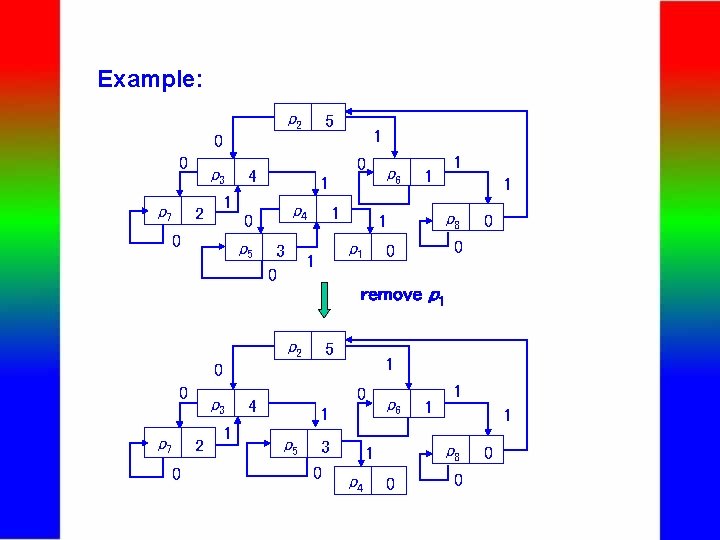
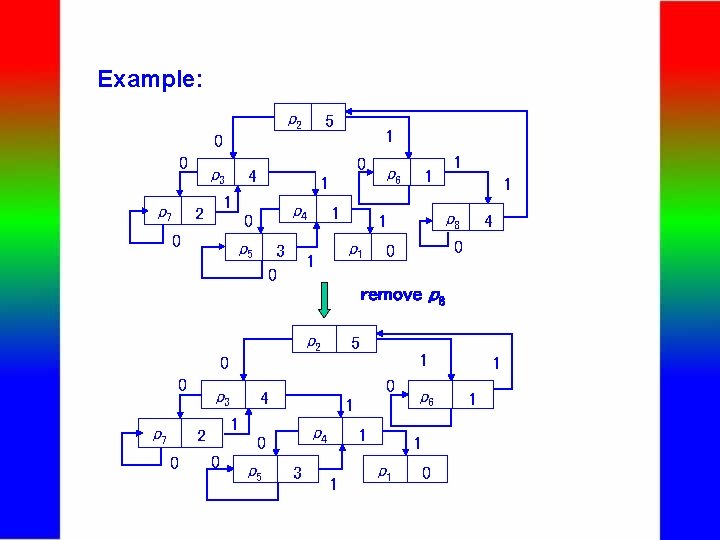
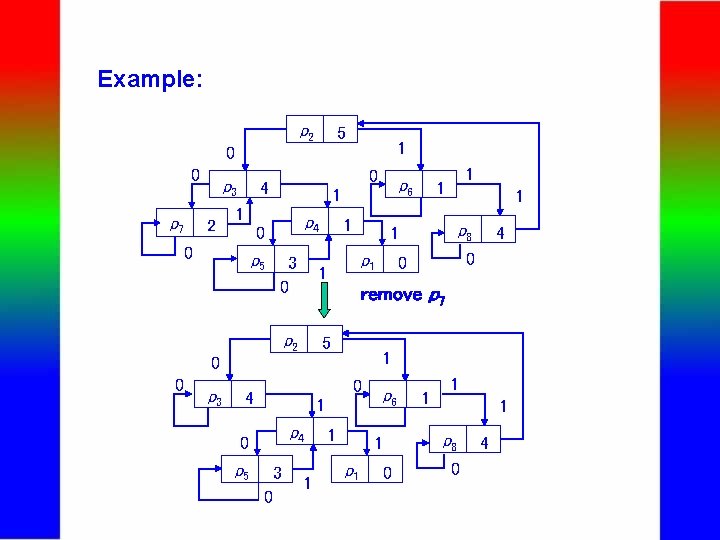
Maintenance of Signature Graph - Insertion of a signature s into G Same as the construction of a signature graph - Deletion of a signature s from G (i) Search G from the root until a node v is encountered, which is marked or skip(v) = 0. (ii) If skip(v) = 0, Compare p(v) and s. If s matches p(v) exactly, do the following; otherwise, nothing will be done. Let v 1 . . . vk-1 vk v be the path explored. Let u 1 be another child of vk (not on the path). Remove vk-1 vk, vk u 1 and v; and generate a new edge vk-1 u 1. skip(vk) : = 0.

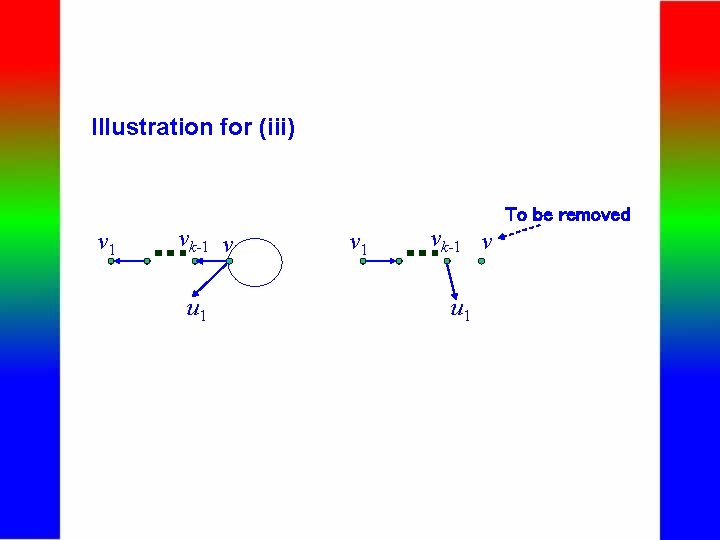
Maintenance of Signature Graph - Deletion of a signature s from G (continued) (iii) If skip(v) 0, Compare p(v’s father) and s. If s matches p(v’s father) exactly, do the following; otherwise, nothing will be done. Let v 1 . . . vk-1 vk v be the path explored. If vk v, replace p(v) with p(vk). Let u 1 be another child of vk (not on the path). Let u 2 be another parent of vk (not on the path). Replace vk-1 vk with vk u 1, and replace vk v with u 2 v. Remove vk. Note that u 2 can be found by searching G from vk with the target signature being p(vk). If vk = v, replace vk with vk-1 u 1. Remove vk.

Maintenance of Signature Graph Illustration for (ii) To be removed v 1 vk-1 vk … u 1 v u 2

Example: p 2 5 1 0 0 p 7 p 3 2 0 4 1 1 p 4 0 0 p 5 3 0 1 5 p 7 2 0 1 1 p 8 0 0 0 1 0 p 3 1 remove p 1 p 2 0 1 1 p 6 0 4 1 p 5 p 6 3 1 0 p 0 4 1 1 1 p 8 0 0

Maintenance of Signature Graph Illustration for (iii) To be removed v 1 vk-1 vk … u 1 v u 2

Example: p 2 5 1 0 0 p 7 p 3 0 4 1 1 2 p 4 0 0 p 5 3 0 1 p 7 5 0 4 1 p 4 0 0 p 5 4 0 1 2 1 p 8 0 0 p 3 1 remove p 8 p 2 0 1 1 p 6 3 1 1 p 6 1 p 1 0 1 1

Illustration for (iii) To be removed v 1 vk-1 v … u 1

Example: p 2 5 1 0 0 p 7 p 3 2 0 4 1 1 p 4 0 0 p 5 1 p 1 3 0 1 p 2 5 p 3 p 5 1 p 8 4 0 0 1 p 4 3 0 1 remove p 7 4 0 1 1 0 0 p 6 1 1 p 6 1 p 1 0 1 1 1 p 8 0 4

Summary and Future Work - Signature and signature file - Signature graph Construction of a signature graph Search of a signature graph Maintenance of a signature graph Future work: Apply signature techniques to evaluation of path-oriented queries in document databases.