Constructing CONJECTURES Constructing CONJECTURES Generating examples Getting literature

Constructing CONJECTURES

Constructing CONJECTURES Generating examples Getting literature

Definition of 132 -pattern Let [n] = {1, 2, …, n}. p = a 1 a 2…an is a permutation of [n]. Consider ai, aj, ak, 1≤i<j<k≤n. High Low a 1 a 2. . . ai. . . Mid aj. . . ak. . . an-1 an If ai < ak < aj, then we say that the ai, aj and ak of p form a 132 -pattern.

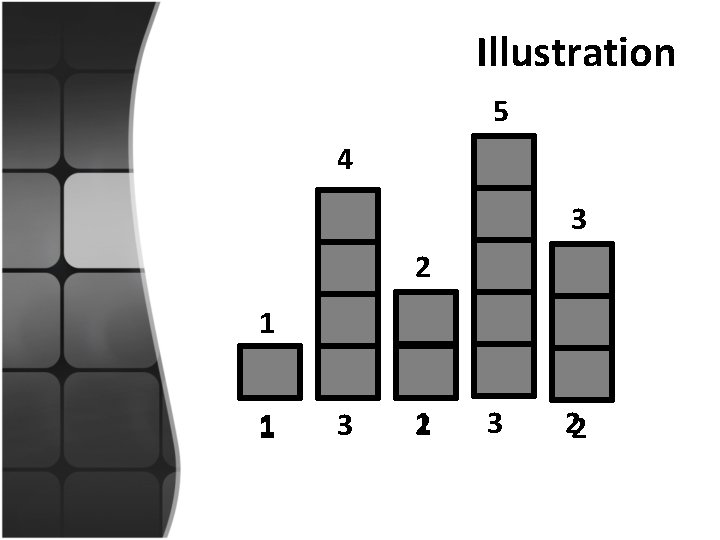
Illustration 5 4 3 2 1 1 3 1 2 3 22

Definition of 132 -avoiding permutation If there are no entries in p that form a 132 pattern, then p is said to be 132 -avoiding.

SHUFFLING s(p) p == a 1 a 2 … an-1 an an+1 an+2… a 2 n-1 a 2 n an+1 an+2 a…n+1 an+2 a 2 n-1 … a 2 n-1 a 2 n *animation by BP Dela Cruz

First Problem How many 132 -avoiding permutations of [2 n] are there such that the shuffles are also 132 -avoiding?

Counts via Scilab/Fortran 2 n 2 4 6 8 10 No. of tests for No. of p = (2 n)! each p = C(2 n, 3) 1 2! = 2 4! = 24 C(4, 3) = 4 6! = 720 C(6, 3) = 20 8! = 40, 320 C(8, 3) = 56 10! = 3, 628, 800 C(10, 3) = 120

Counts via Scilab/Fortran 2 n 2 4 6 8 10 No. of tests for No. of s(p) = (2 n)! each s(p) = C(2 n, 3) 1 2! = 2 4! = 24 C(4, 3) = 4 6! = 720 C(6, 3) = 20 8! = 40, 320 C(8, 3) = 56 10! = 3, 628, 800 C(10, 3) = 120

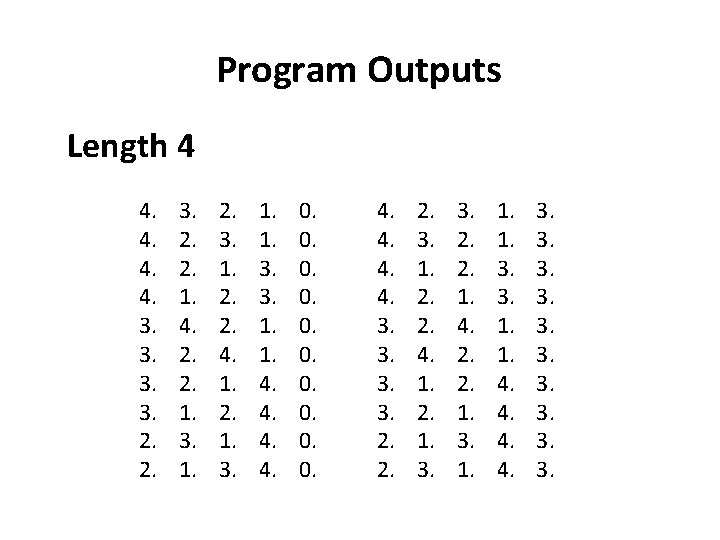
Program Outputs Length 4 4. 4. 3. 3. 2. 2. 1. 4. 2. 2. 1. 3. 1. 2. 3. 1. 2. 2. 4. 1. 2. 1. 3. 1. 1. 3. 3. 1. 1. 4. 4. 0. 0. 0. 4. 4. 3. 3. 2. 2. 3. 1. 2. 2. 4. 1. 2. 1. 3. 2. 2. 1. 4. 2. 2. 1. 3. 1. 1. 3. 3. 1. 1. 4. 4. 3. 3. 3.

Program Outputs Length 6

Program Outputs Length 8

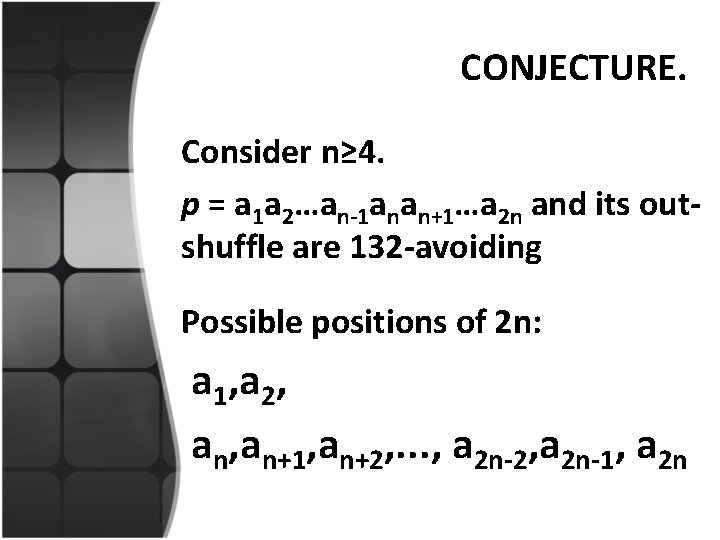
CONJECTURE. Consider n≥ 4. p = a 1 a 2…an-1 anan+1…a 2 n and its outshuffle are 132 -avoiding Possible positions of 2 n: a 1, a 2, an+1, an+2, . . . , a 2 n-2, a 2 n-1, a 2 n

Proposition. (BP Dela Cruz) For a 132 -avoiding permutation of [2 n] of length n≥ 4 with a 132 avoiding shuffle, ak 2 n when 3 ≤ k ≤ n-1.

Summary of Counts Position of 2 n a 1 a 2 an an+1 an+k, 2≤k ≤n-2 a 2 n-1 a 2 n Counts 2 n 2 -4 n+6 1 n-1 2 k(n-k) 2 n-2

MAJOR RESULT Proposition. (BP Dela Cruz) For n≥ 3, number of 132 -avoiding permutations with 132 avoiding (out-)shuffle of [2 n]:

Related literature and conjectures • A 2 -connected graph is hamiltonian if it is K 1, 3 P 5 -free or K 1, 3 P 6 -free (Broersma, Veldman, 1990). • A 2 -connected, K 1, 3 P 5 -free graph is pancyclic if its order (Faudree, et. al, 1995). • A 3 -connected graph is hamiltonianconnected if it is K 1, 3 P 5 -free or K 1, 3 P 5 -free (Broersma et. al. , 2002).

Related literature and conjectures Conjecture 1. A 2 -connected, K 1, 3 P 5 -free graph is 1 -edge hamiltonian. Conjecture 2. A 2 -connected, K 1, 3 P 5 -free graph is 2 -edge hamiltonian.

Theorem. If G is a 2 -connected K 1, 3 P 4 -free graph, |V(G)|≥ 4, with a minimum vertex cut of k vertices, then G is isomorphic to a (Km U Kn)+Hk where Hk is a K 1, 3 P 4 –free graphs on k vertices of at most 2 components. Moreover, if Hk has 2 components, then Hk is a union of 2 complete graphs.

Related literature and conjectures • A 2 -connected, K 1, 3 Z 2 -free graph of order n≥ 3 is pancyclic except cycles (Gould, Jacobson, 1982). • A 2 -connected graph is hamiltonian if it is K 1, 3 Z 2 -free or K 1, 3 Z 3 -free of order n≥ 10 (Faudree, et. al. , 1995). • A 2 -connected K 1, 3 Z 2 -free of order n≥ 10 is cycle-extendable (Faudree, Gould, 1997). • A 3 -connected graph is hamiltonianconnected if it is K 1, 3 Z 2 -free or K 1, 3 Z 3 -free (Broersma, et. al. , 2002).

Related literature and conjectures Conjecture 3. A 2 -connected, K 1, 3 Z 2 -free graph is 1 -edge hamiltonian. Conjecture 4. A 2 -connected, K 1, 3 Z 2 -free graph is 2 -edge hamiltonian.

Theorem. Every 2 -connected K 1, 3 Z 1 -free graph is 1 -edge hamiltonian except for (K 1 U K 1)+K 2.

Theorem. Every k-connected K 1, 3 Z 1 -free graph, k≥ 2, is k-edge hamiltonian except for (K 1 U K 1)+K 2.

Theorem. Every 2 -connected K 1, 3 Z 2 -free graph is 1 -edge hamiltonian except for six exceptional graphs.

Non-1 -edge hamiltonian 2 -connected K 1, 3 Z 2 -free graphs

OBJECTIVES • Examine the conjectures by extending existing results on hamiltonian properties. • Examine (not established) hamiltonianproperties related to the conjectures. • Add (or relax) the conditions to establish results on 1 -edge hamiltonicity or 2 -edge hamiltonicity. • If possible, come up with generalized results.

Generating examples/ getting literature ORGANIZE (Look for patterns) Understanding conjecture Evaluating conjecture Writing conjecture Testing conjecture

Understanding/evaluating CONJECTURES • READ. • COMPARE. • Generate examples and non-examples. • Be careful of counterexamples. • Identify the suitable conditions.

Writing CONJECTURES Some pointers • Does the conjecture appear to be true or false? • Is it obvious or subtle? • Is it easy or difficult to understand? • Is the conjecture general? • Is it specific enough?

Constructing CONJECTURES