Constructing an ALU What is it The device

Constructing an ALU • What is it? – The device that does: • Addition and subtraction • Logical operations (and, or) • Support for conditional branching: slt, beq, bne • What is it built from? • AND gates, OR gates, Inverters, Multiplexors • Real technologies may use other building blocks, but the ideas are similar 1

Constructing an ALU: Key Ideas • Design a 1 -bit ALU that performs – – Logical operations OR, AND Addition Subtraction Comparison: • SLT (Set on Less Than) • BEQ, BNE (Branch if Equal, Branch if Not Equal) • Connect 32 together to form a 32 -bit wide ALU – The obvious way is called ripple carry – A faster way that is not much more expensive is called carry lookahead 2

Constructing an ALU: Implementing AND and OR • • Sometimes we want to output a AND b Sometimes we want to output a OR b How do we choose between them? AND gate, OR gate, select with multiplexor 3

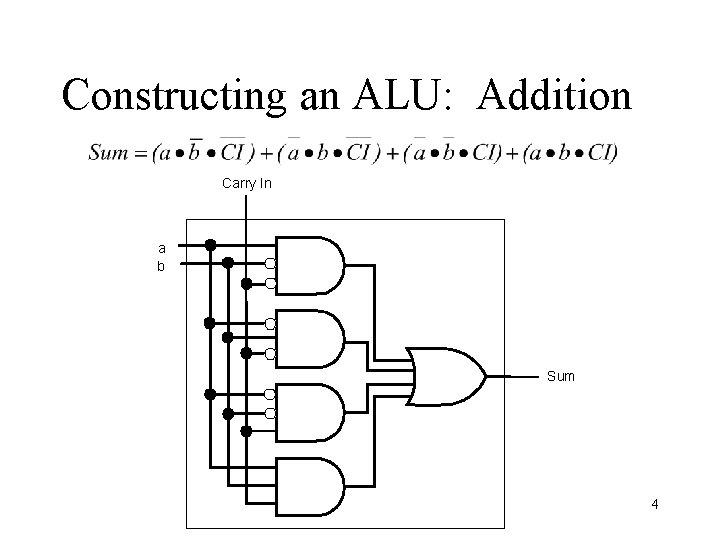
Constructing an ALU: Addition Carry In a b Sum 4

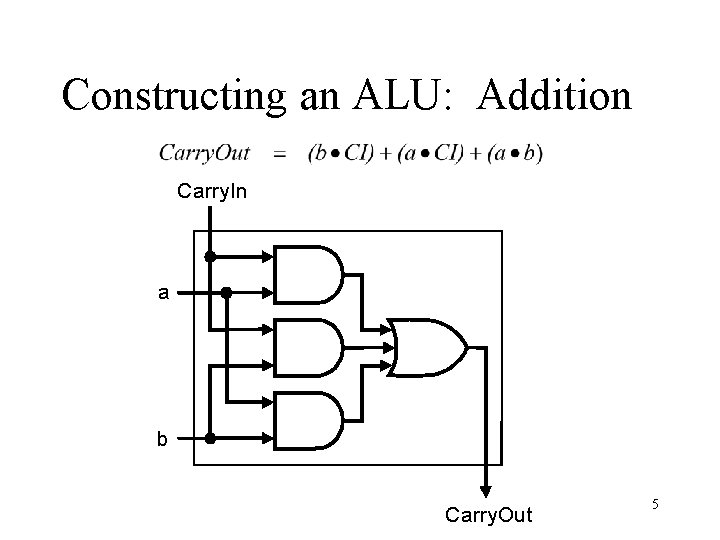
Constructing an ALU: Addition Carry. In a b Carry. Out 5

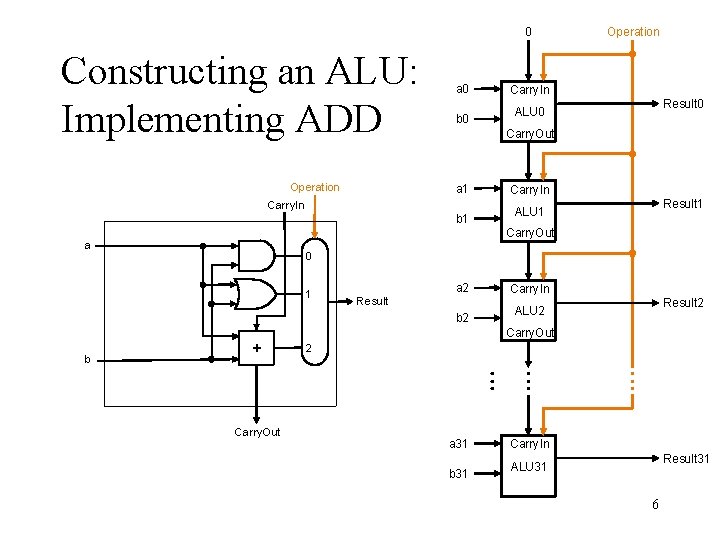
0 Constructing an ALU: Implementing ADD Operation a 0 b 0 Operation Carry. In Result 0 ALU 0 Carry. Out a 1 Carry. In b 1 Carry. In Result 1 ALU 1 Carry. Out a 0 1 a 2 Result b 2 Carry. In Result 2 ALU 2 Carry. Out 2 b Carry. Out a 31 b 31 Carry. In Result 31 ALU 31 6

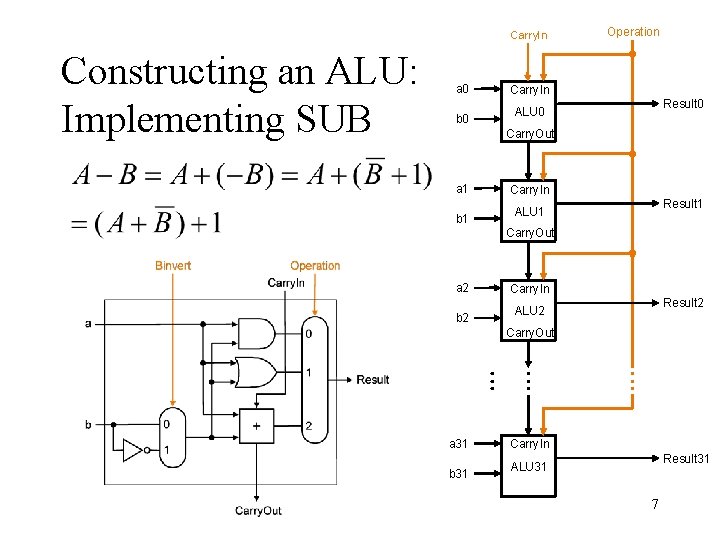
Carry. In Constructing an ALU: Implementing SUB a 0 b 0 Operation Carry. In Result 0 ALU 0 Carry. Out a 1 b 1 Carry. In Result 1 ALU 1 Carry. Out a 2 b 2 Carry. In Result 2 ALU 2 Carry. Out a 31 b 31 Carry. In Result 31 ALU 31 7

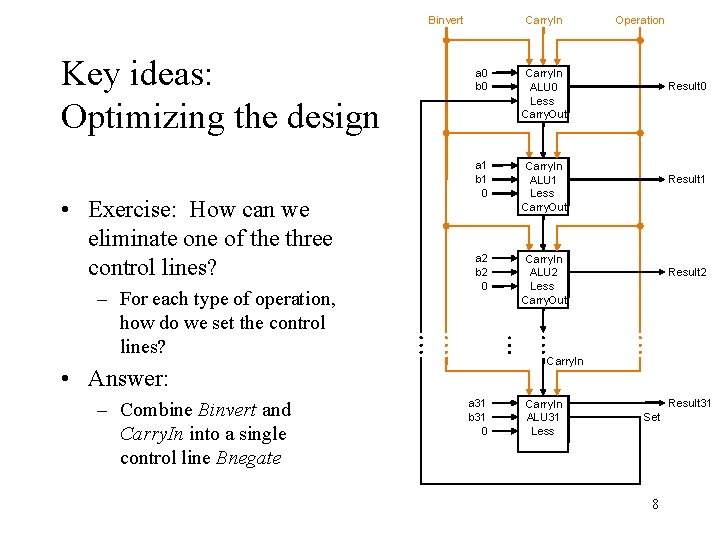
Binvert Key ideas: Optimizing the design • Exercise: How can we eliminate one of the three control lines? – For each type of operation, how do we set the control lines? Carry. In a 0 b 0 Carry. In ALU 0 Less Carry. Out a 1 b 1 0 Carry. In ALU 1 Less Carry. Out a 2 b 2 0 Carry. In ALU 2 Less Carry. Out Result 0 Result 1 Result 2 Carry. In • Answer: – Combine Binvert and Carry. In into a single control line Bnegate Operation a 31 b 31 0 Carry. In ALU 31 Less Result 31 Set 8

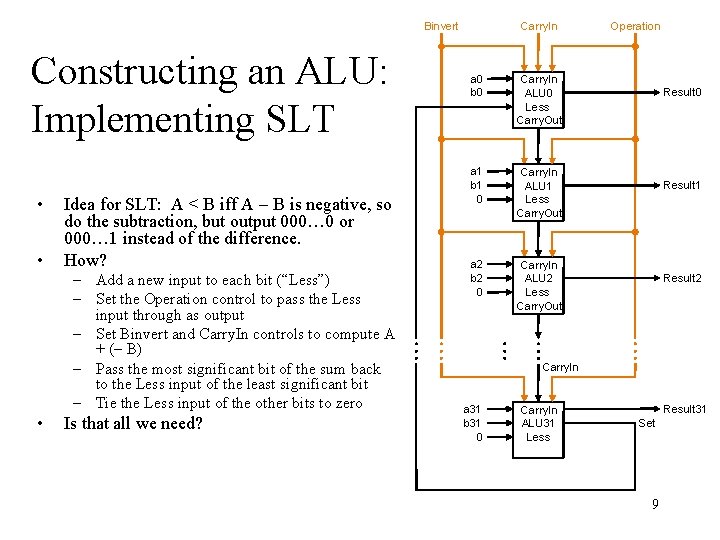
Binvert Constructing an ALU: Implementing SLT • • Idea for SLT: A < B iff A B is negative, so do the subtraction, but output 000… 0 or 000… 1 instead of the difference. How? – Add a new input to each bit (“Less”) – Set the Operation control to pass the Less input through as output – Set Binvert and Carry. In controls to compute A + ( B) – Pass the most significant bit of the sum back to the Less input of the least significant bit – Tie the Less input of the other bits to zero • Is that all we need? Carry. In a 0 b 0 Carry. In ALU 0 Less Carry. Out a 1 b 1 0 Carry. In ALU 1 Less Carry. Out a 2 b 2 0 Carry. In ALU 2 Less Carry. Out Operation Result 0 Result 1 Result 2 Carry. In a 31 b 31 0 Carry. In ALU 31 Less Result 31 Set 9

Constructing an ALU: Implementing SLT • What if there is overflow? • Exercise: How do we detect overflow? • Answer: Homework exercise. Hint: – If we add two numbers with the same sign, what sign should the result have? – If we subtract numbers with different signs, what sign should the result have? 10

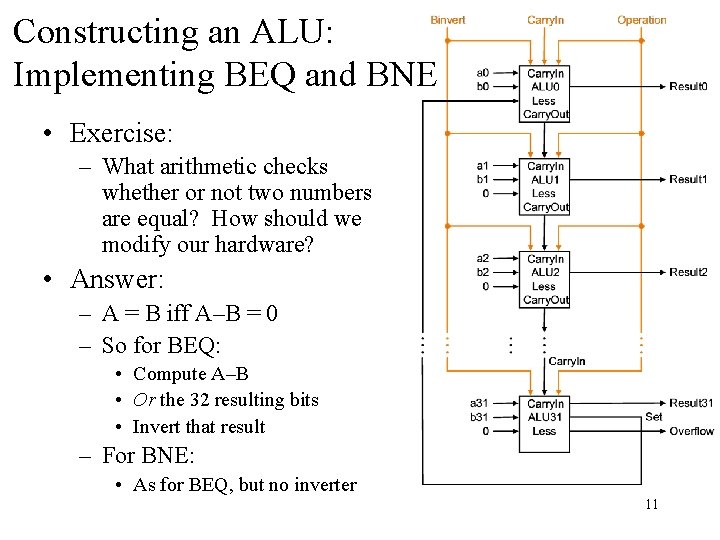
Constructing an ALU: Implementing BEQ and BNE • Exercise: – What arithmetic checks whether or not two numbers are equal? How should we modify our hardware? • Answer: – A = B iff A–B = 0 – So for BEQ: • Compute A–B • Or the 32 resulting bits • Invert that result – For BNE: • As for BEQ, but no inverter 11

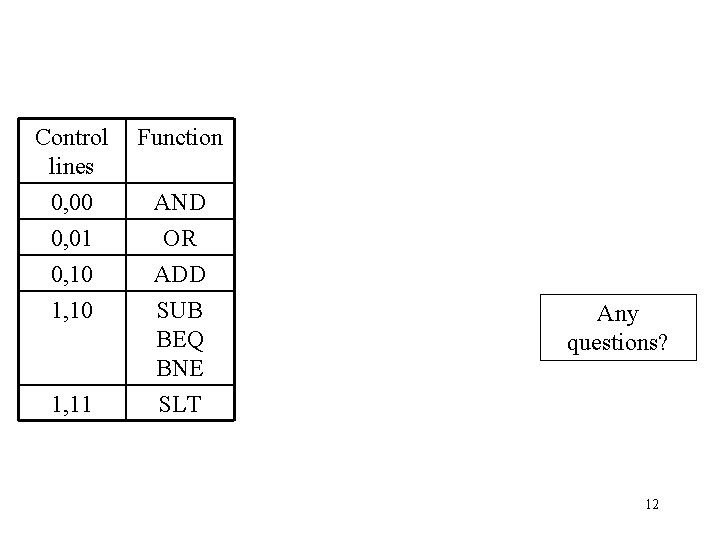
Control lines 0, 00 0, 01 Function 0, 10 1, 10 ADD SUB BEQ BNE SLT 1, 11 AND OR Any questions? 12

Constructing an ALU: Self-assessment • Modify the ALU to implement each of the following: – Bitwise NOR, bitwise XOR, … – Bitwise NOT – Logical AND, logical OR, … – Logical NOT – SIGN 13

Carry lookahead • The problem: – Leftmost bit of the sum must wait for the sequential evaluation of all 32 1 -bit adders. Too slow! • A preliminary solution: – Theorem: Any logic equation can be implemented using at most 2 levels of logic. – So implement addition using two levels of logic! – Very fast, but uses an astronomical number of gates. Hence impractical. • A better solution: carry lookahead – For an n-bit adder, needs log 2 n levels of logic. – Number of gates required is practical. 14

Why study carry lookahead? • Today, understand: – the basic idea – details as best you can follow them • See the details in the text as needed – For example, if you implement carry lookahead in your project! • Carry lookahead provides excellent examples of – the use of abstraction to invent a design with improved performance – space versus time tradeoffs in logic design 15

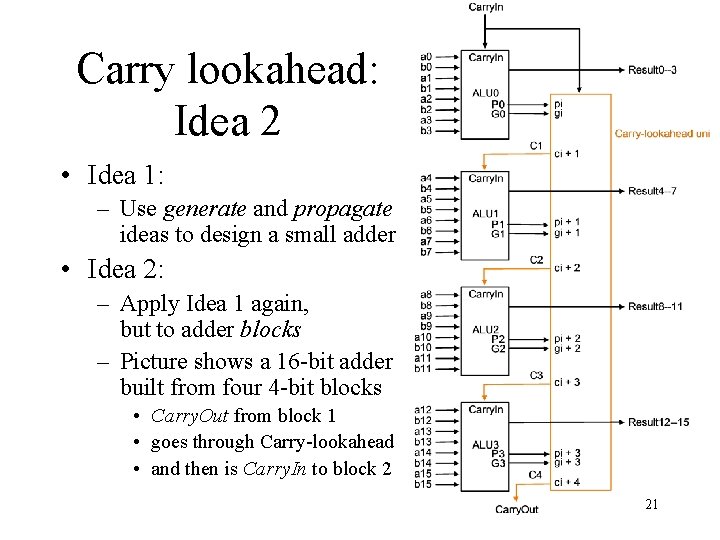
Carry lookahead: the basic ideas • Can implement addition using two-level logic. – But too many gates! • We seek a compromise solution: – more than two levels of logic – but fewer gates. • Idea 1: – Use generate and propagate ideas to design a small adder (say, 4 -bit). See next slide. • Idea 2: – Apply Idea 1 again, but to adder blocks (say, to four 4 bit blocks). See later slides. 16

Carry lookahead: Idea 1 • Idea 1: – Use generate and propagate ideas to design a small adder (say, 4 -bit). • Exercise: – Consider a 4 -bit adder: a 3 a 2 a 1 a 0 + b 3 b 2 b 1 b 0 – When is the Carry. Out bit of the result equal to 1? • Examples: 1000 + 1000 0100 1100 0010 1110 0110 1010 • Hints: generated by what? propagated through what? 17

Carry lookahead: Idea 1 • Consider a 4 -bit adder: a 3 a 2 a 1 a 0 + b 3 b 2 b 1 b 0 – When is the Carry. Out bit of the result equal to 1? • Answer: – if a 3 and b 3 are 1 s • Generated by bit 3 – if (a 2 and b 2 are 1 s) AND (a 3 or b 3 are 1 s) • Generated by bit 2, propagated through bit 3 – if (a 1 and b 1 are 1 s) AND (a 2 or b 2 are 1 s) AND (a 3 or b 3 are 1 s) • Generated by bit 1, propagated through bits 2 and 3 – if. . . generated by bit 0, propagated through bits 1, 2, 3 18

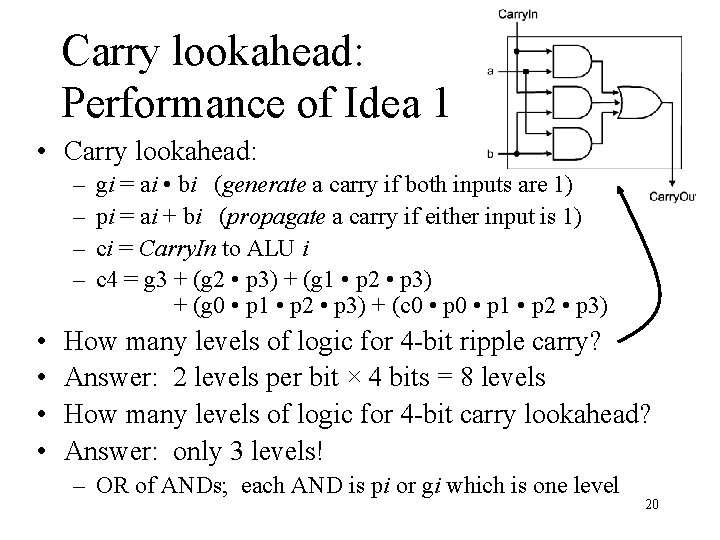
Carry lookahead: Idea 1 • Define: – gi = ai • bi (generate a carry if both inputs are 1) – pi = ai + bi (propagate a carry if either input is 1) – ci = Carry. In to ALU i • Then, as seen on the previous slide: – – c 1 = g 0 + (c 0 • p 0) c 2 = g 1 + (g 0 • p 1) + (c 0 • p 1) c 3 = g 2 + (g 1 • p 2) + (g 0 • p 1 • p 2) + (c 0 • p 1 • p 2) c 4 = g 3 + (g 2 • p 3) + (g 1 • p 2 • p 3) + (g 0 • p 1 • p 2 • p 3) + (c 0 • p 1 • p 2 • p 3) 19

Carry lookahead: Performance of Idea 1 • Carry lookahead: – – • • gi = ai • bi (generate a carry if both inputs are 1) pi = ai + bi (propagate a carry if either input is 1) ci = Carry. In to ALU i c 4 = g 3 + (g 2 • p 3) + (g 1 • p 2 • p 3) + (g 0 • p 1 • p 2 • p 3) + (c 0 • p 1 • p 2 • p 3) How many levels of logic for 4 -bit ripple carry? Answer: 2 levels per bit × 4 bits = 8 levels How many levels of logic for 4 -bit carry lookahead? Answer: only 3 levels! – OR of ANDs; each AND is pi or gi which is one level 20

Carry lookahead: Idea 2 • Idea 1: – Use generate and propagate ideas to design a small adder • Idea 2: – Apply Idea 1 again, but to adder blocks – Picture shows a 16 -bit adder built from four 4 -bit blocks • Carry. Out from block 1 • goes through Carry-lookahead • and then is Carry. In to block 2 21

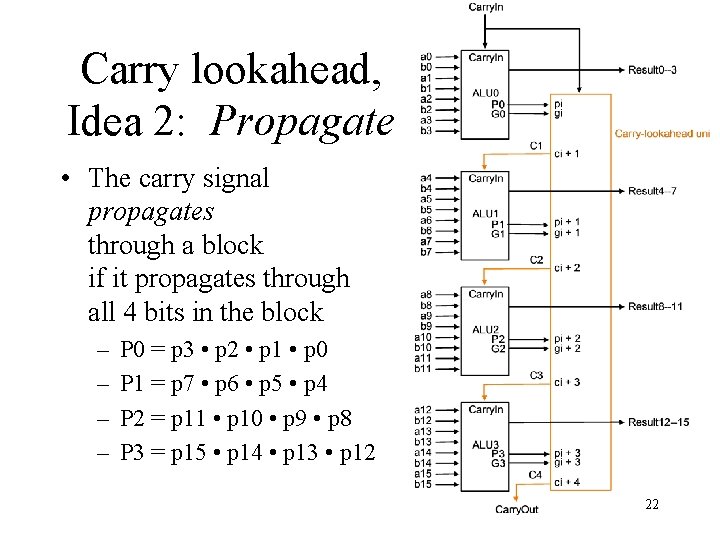
Carry lookahead, Idea 2: Propagate • The carry signal propagates through a block if it propagates through all 4 bits in the block – – P 0 = p 3 • p 2 • p 1 • p 0 P 1 = p 7 • p 6 • p 5 • p 4 P 2 = p 11 • p 10 • p 9 • p 8 P 3 = p 15 • p 14 • p 13 • p 12 22

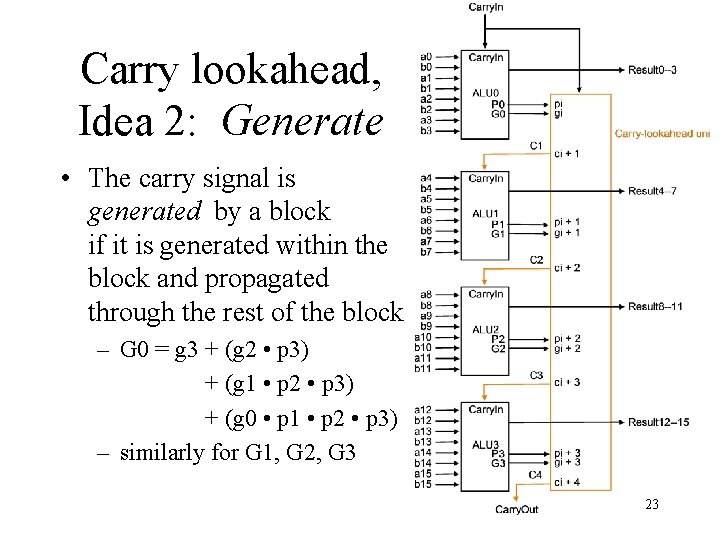
Carry lookahead, Idea 2: Generate • The carry signal is generated by a block if it is generated within the block and propagated through the rest of the block – G 0 = g 3 + (g 2 • p 3) + (g 1 • p 2 • p 3) + (g 0 • p 1 • p 2 • p 3) – similarly for G 1, G 2, G 3 23

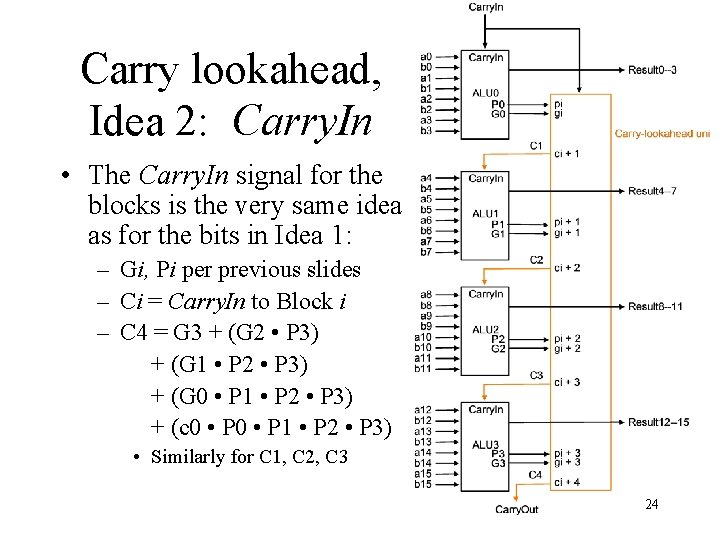
Carry lookahead, Idea 2: Carry. In • The Carry. In signal for the blocks is the very same idea as for the bits in Idea 1: – Gi, Pi per previous slides – Ci = Carry. In to Block i – C 4 = G 3 + (G 2 • P 3) + (G 1 • P 2 • P 3) + (G 0 • P 1 • P 2 • P 3) + (c 0 • P 1 • P 2 • P 3) • Similarly for C 1, C 2, C 3 24

Carry lookahead: performance – 16 -bit carry lookahead: • • gi = ai • bi pi = ai + bi ci = Carry. In to ALU i P 0 = p 3 • p 2 • p 1 • p 0 G 0 = g 3 + (g 2 • p 3) + (g 1 • p 2 • p 3) + (g 0 • p 1 • p 2 • p 3) C 4 = G 3 + (G 2 • P 3) + (G 1 • P 2 • P 3) + (G 0 • P 1 • P 2 • P 3) + (c 0 • P 1 • P 2 • P 3) • Similarly for other Pi, Gi, Ci. – – How many levels of logic for 16 -bit ripple carry? Answer: 2 levels per bit × 8 bits = 32 levels How many levels of logic for 16 -bit carry lookahead? Answer: 5 levels! Over six-fold improvement! • OR of ANDs; each AND is Pi (2 levels) or Gi (3 levels) 25

Carry lookahead: summary • Ripple-carry: – Too slow, because carries are computed sequentially • Could do addition in just 2 layers of logic – Very fast, but way too many gates • Space versus time tradeoff • Carry lookahead: a practical compromise – Speed is proportional to the log of the number of bits – Number of gates required is practical – Designed using two ideas: • Idea 1: Write equations using generate and propagate terms • Idea 2: Apply idea 1 to 4 -bit adder, then again to 4 blocks of 4 bit adders 26