Constraint Satisfaction Problem Chapter 6 These slides were

Constraint Satisfaction Problem Chapter 6 [These slides were created by Dan Klein and Pieter Abbeel for CS 188 Intro to AI at UC Berkeley. All CS 188 materials are available at http: //ai. berkeley. edu. ]

Motivations § Previously, each problem has its own representation of state, its own data structure. § We want to standardize state representation. § Each state is represented by variables and their particular assigned values.

Map coloring problem § Variables: § A variable is assigned or instantiated a value. § Domains: Size of D is d=3. § Constraints: adjacent regions must have different colors Implicit: Explicit: § A solution is a set of pairs satisfying all constraints. How many colors do we need to color all the countries on planet earth so that no two adjacent countries have the same color?

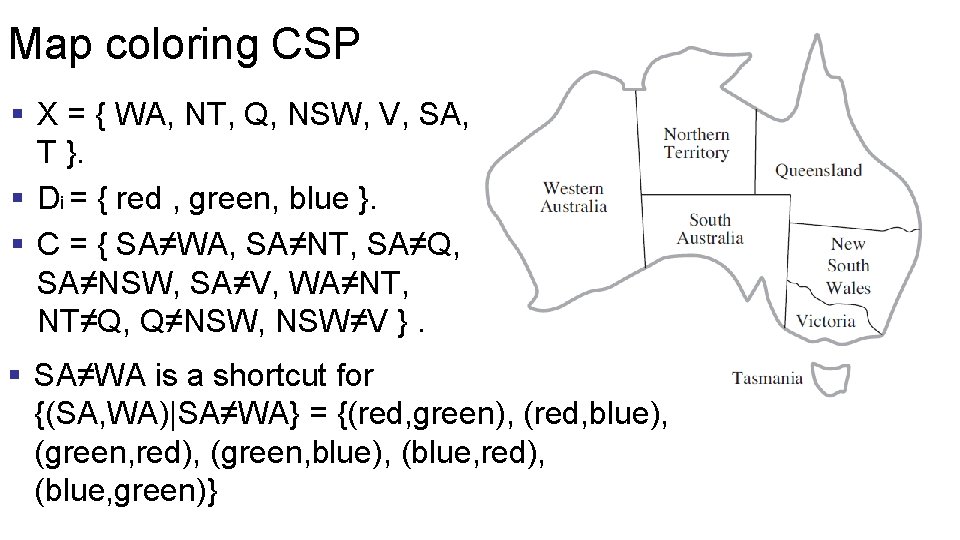
Map coloring CSP § X = { WA, NT, Q, NSW, V, SA, T }. § Di = { red , green, blue }. § C = { SA≠WA, SA≠NT, SA≠Q, SA≠NSW, SA≠V, WA≠NT, NT≠Q, Q≠NSW, NSW≠V }. § SA≠WA is a shortcut for {(SA, WA)|SA≠WA} = {(red, green), (red, blue), (green, red), (green, blue), (blue, red), (blue, green)}

CSP assignment states § Each CSP state is an assignment or assignment state. § An assignment is a set of variable=value pairs. {WA=red, Q=red, V=green} § A partial assignment is one that assigns values to some of the variables. {WA=red, Q=red}. § An assignment that does not violate any constraints is called a consistent or legal assignment. {WA=red, NT=green} § A complete assignment is one in which every variable is assigned. {WA=red, NT=red, Q=red , NSW=green, V=red, SA=blue, T=red} § A solution to a CSP is a consistent, complete assignment. {WA=red, NT=green, Q=red , NSW=green, V=red, SA=blue, T=red}

Factored representation of state § § § Each state is represented as a set of pairs. Each pair is variable (attribute) and its value. Attribute-value pair Two different atomic states are just 2 different black boxes Two different factored states can share some attributes. This makes it much easier to work out how to turn one state into another.

N-Queens Formulation 1 • Variables: • Domains: • Constraints No rows can have two 1 s.

What is a CSP problem? § A constraint satisfaction problem is a triple: 1. X is a set of variables, {X 1, . . . , Xn}. 2. D is a set of domains, {D 1, . . . , Dn}, one for each variable. 3. C is a set of constraints that specify allowable combinations of values. § Find an assignment to satisfy the constraints. § CSP is NP-complete.

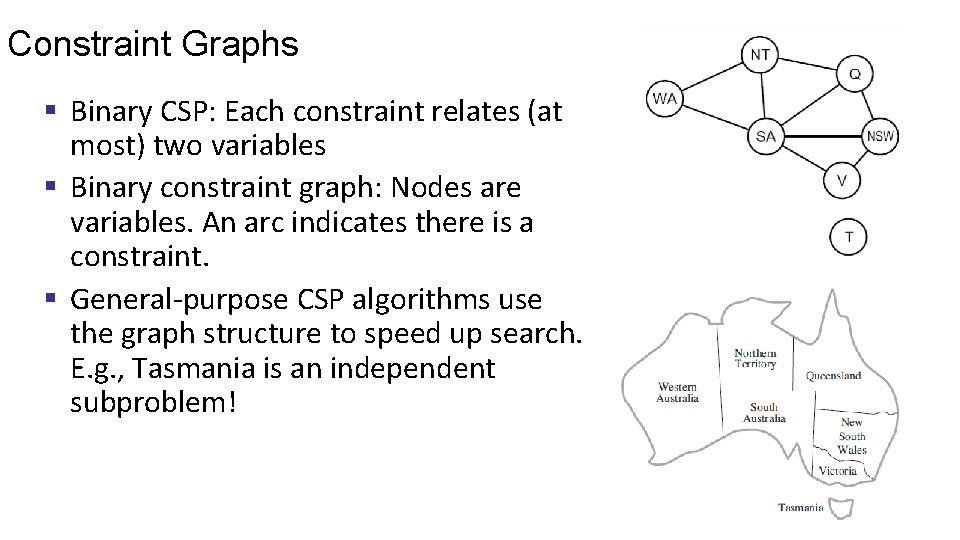
Constraint Graphs § Binary CSP: Each constraint relates (at most) two variables § Binary constraint graph: Nodes are variables. An arc indicates there is a constraint. § General-purpose CSP algorithms use the graph structure to speed up search. E. g. , Tasmania is an independent subproblem!

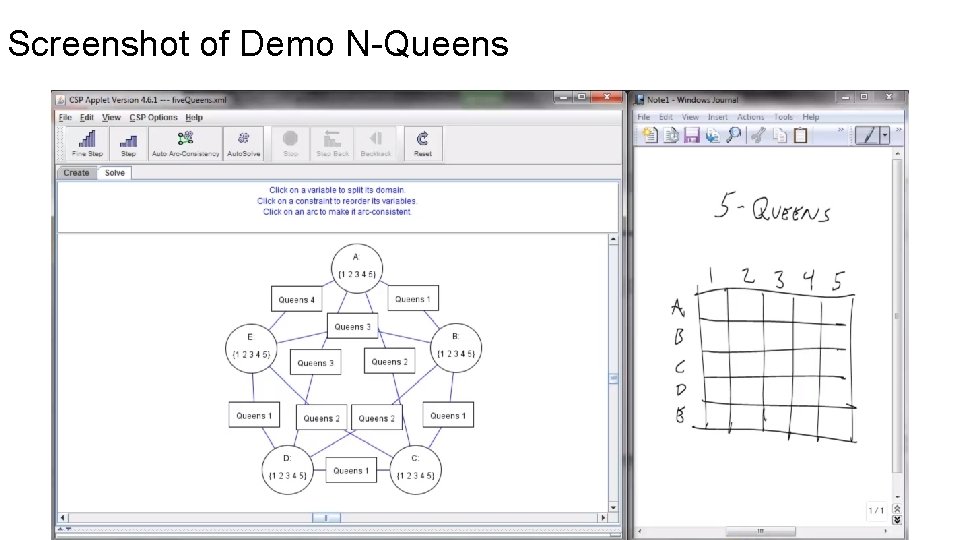
Screenshot of Demo N-Queens

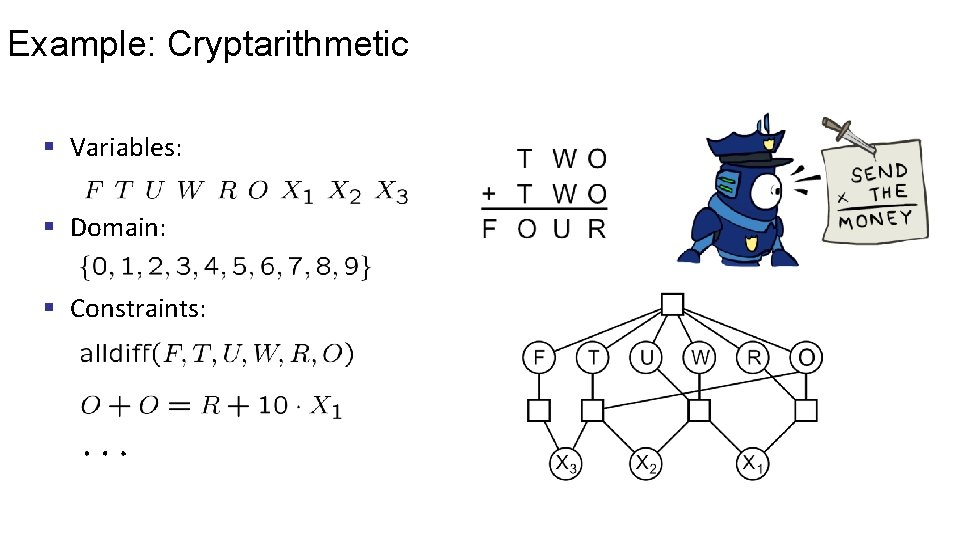
Example: Cryptarithmetic § Variables: § Domain: § Constraints:

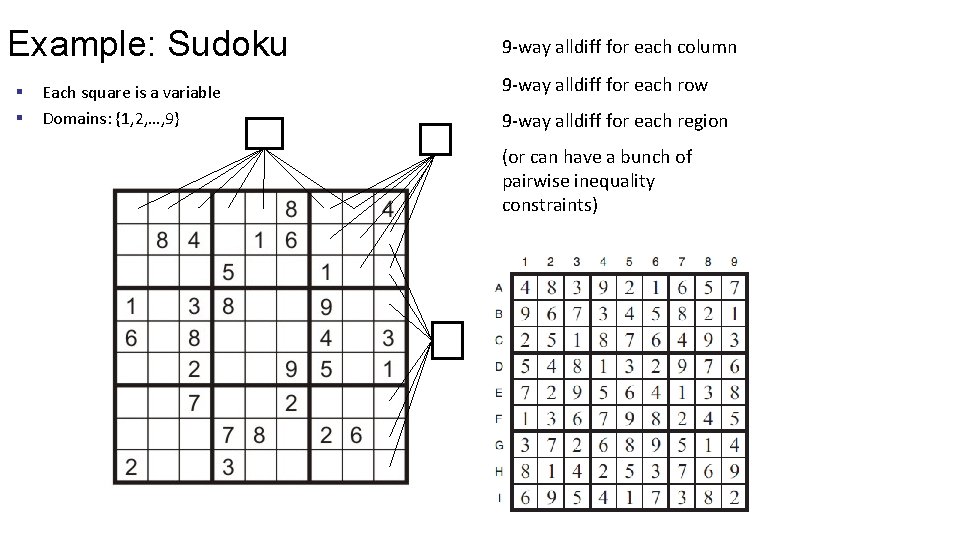
Example: Sudoku § § Each square is a variable Domains: {1, 2, …, 9} 9 -way alldiff for each column 9 -way alldiff for each row 9 -way alldiff for each region (or can have a bunch of pairwise inequality constraints)

Varieties of CSPs § Discrete Variables • Finite domains § Size d means O(dn) complete assignments, n variables § E. g. , Boolean CSPs, including Boolean satisfiability (NPcomplete) • Infinite domains (integers, strings, etc. ) § E. g. , job scheduling, variables are start/end times for each job § Linear constraints solvable, nonlinear undecidable § Continuous variables • E. g. , start/end times for Hubble Telescope observations • Linear constraints solvable in polynomial time by LP methods

Varieties of Constraints § Varieties of Constraints • Unary constraints involve a single variable (equivalent to reducing domains), e. g. : • Binary constraints involve pairs of variables, e. g. : • Higher-order constraints involve 3 or more variables: e. g. , cryptarithmetic column constraints § Preferences (soft constraints): • E. g. , red is better than green • Often representable by a cost for each variable assignment • Gives constrained optimization problems • (We’ll ignore these until we get to Bayes’ nets)

Real-World CSPs § § § § Assignment problems: e. g. , who teaches what class Timetabling problems: e. g. , which class is offered when and where? Hardware configuration Transportation scheduling Factory scheduling Circuit layout Fault diagnosis … lots more! § Many real-world problems involve real-valued variables…

Solving CSPs

Standard Search Formulation § States defined by the values assigned so far (partial assignments) § Initial state: the empty assignment, {} § Successor function: assign a value to an unassigned variable. § Goal test: the current assignment is complete and satisfies all constraints

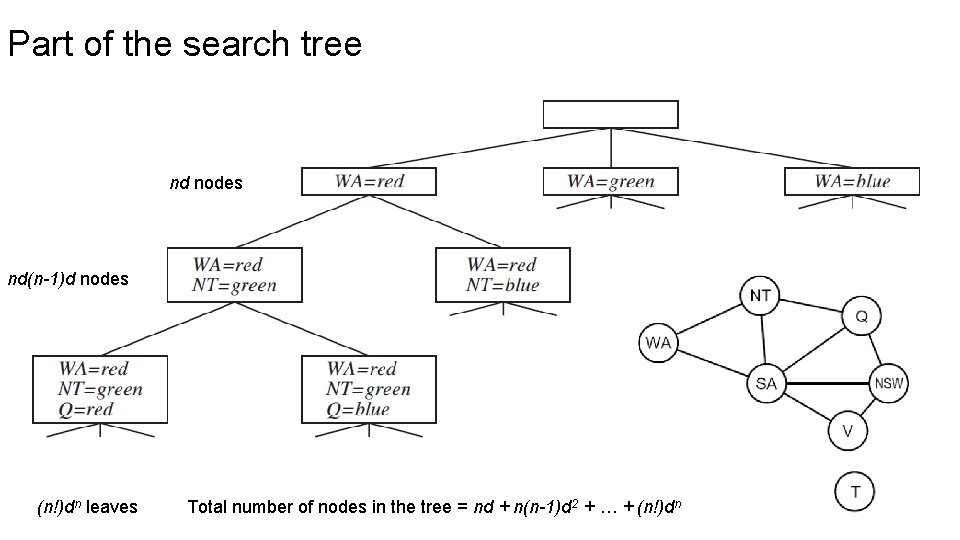
Part of the search tree nd nodes nd(n-1)d nodes (n!)dn leaves Total number of nodes in the tree = nd + n(n-1)d 2 + … + (n!)dn

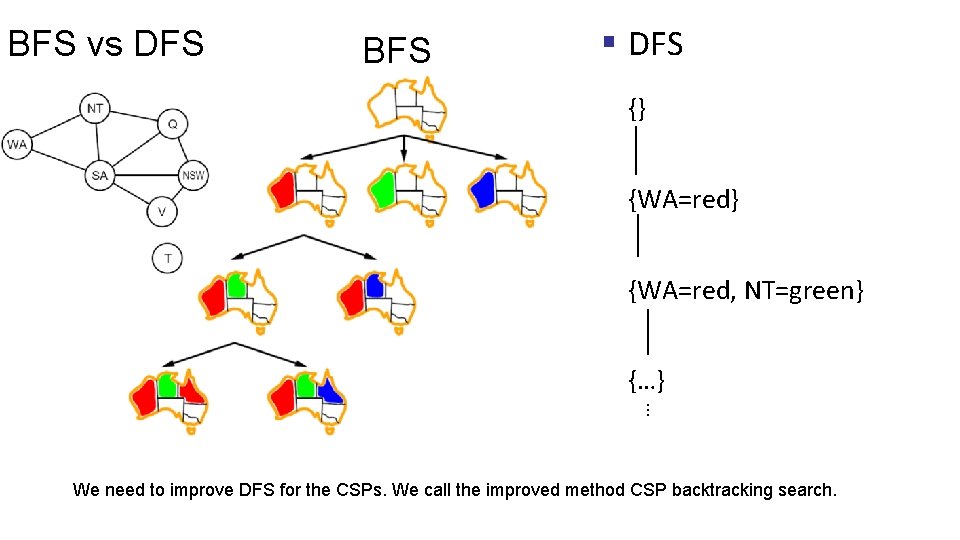
BFS vs DFS BFS § DFS {} {WA=red, NT=green} {…} ⋮ We need to improve DFS for the CSPs. We call the improved method CSP backtracking search.

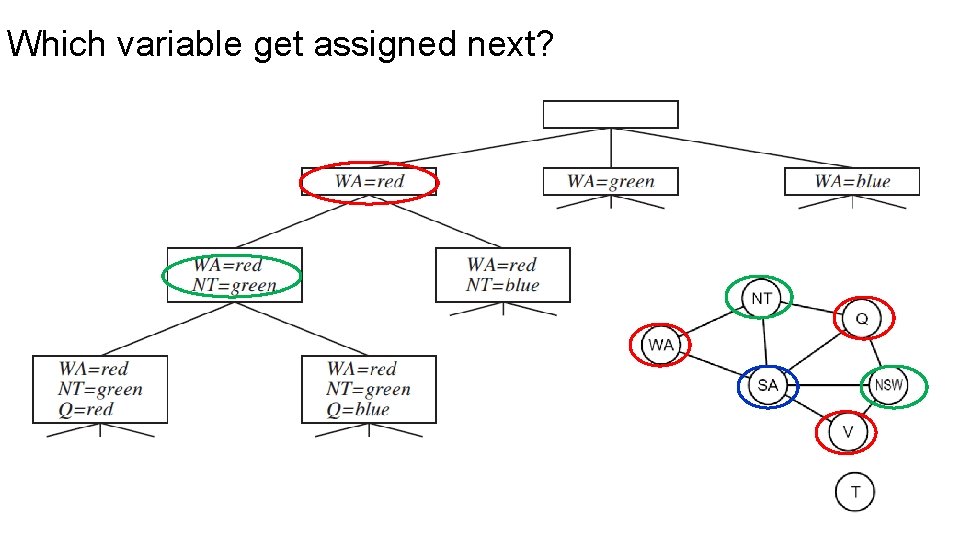
Which variable get assigned next?

Which variable get assigned next? § Choose the variable with the fewest legal values. § Most constrained variable § A variable that is most likely to cause a failure soon, thereby pruning the search tree as early as possible. § Minimum-remaining-values (MRV) heuristic § The MRV heuristic usually performs better than a random or fixed ordering, sometimes by a factor of 1, 000.

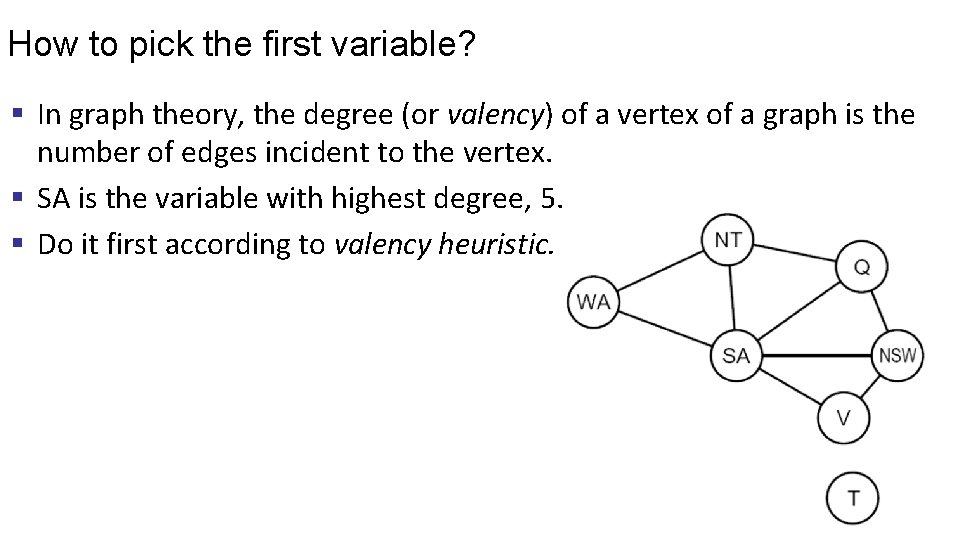
How to pick the first variable? § In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex. § SA is the variable with highest degree, 5. § Do it first according to valency heuristic.

Improving Backtracking § Minimum-remaining-values (MRV) heuristic and valency heuristic improve backtracking by choosing which variable to try next. § After we have picked a variable and its value, can we predict its future success or failure?

Forward Checking § A form of smart inference § Cross off values that violate a constraint after a variable is paired. WA NT Q SA NSW V

Forward Checking runs into problem § Forward checking propagates information from assigned to unassigned variables, but doesn't provide early detection for all failures. WA NT SA Q NSW V NT and SA cannot both be blue! We need Constraint propagation: reasoning from constraint to constraint

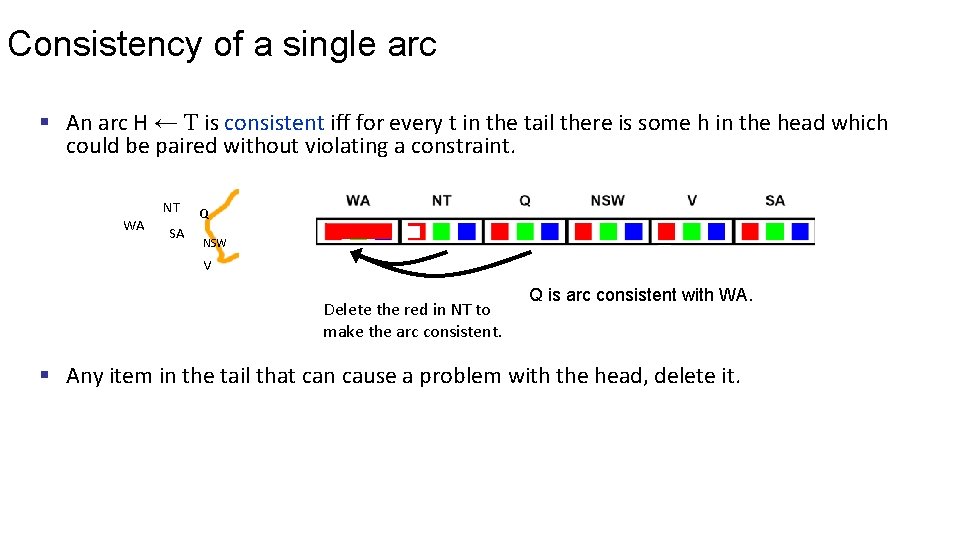
Consistency of a single arc § An arc H ← T is consistent iff for every t in the tail there is some h in the head which could be paired without violating a constraint. WA NT SA Q NSW V Delete the red in NT to make the arc consistent. Q is arc consistent with WA. § Any item in the tail that can cause a problem with the head, delete it.

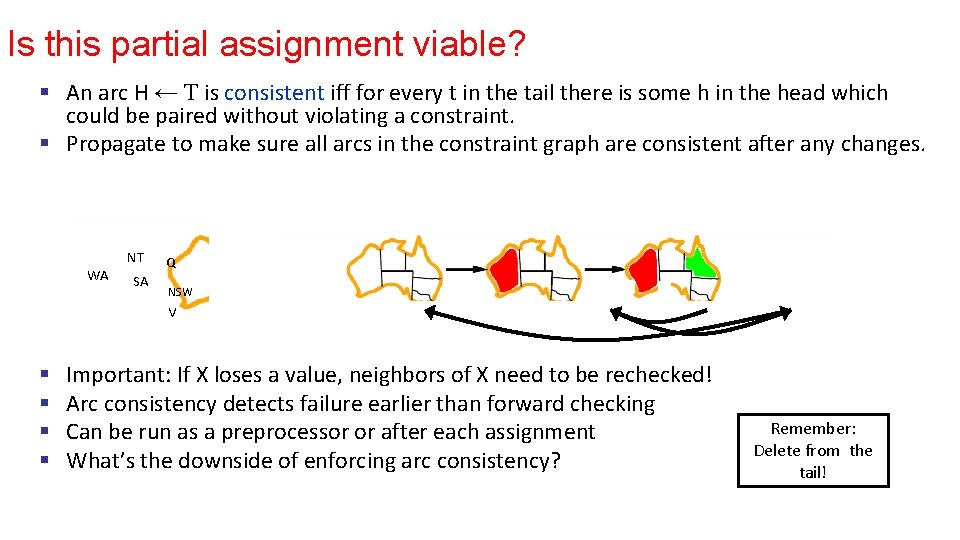
Is this partial assignment viable? § An arc H ← T is consistent iff for every t in the tail there is some h in the head which could be paired without violating a constraint. § Propagate to make sure all arcs in the constraint graph are consistent after any changes. WA NT SA Q NSW V § § Important: If X loses a value, neighbors of X need to be rechecked! Arc consistency detects failure earlier than forward checking Can be run as a preprocessor or after each assignment What’s the downside of enforcing arc consistency? Remember: Delete from the tail!

There are n variables. There are n 2 arcs. d is the size of the domain. For each arc, it can go back into the queue at most d times.

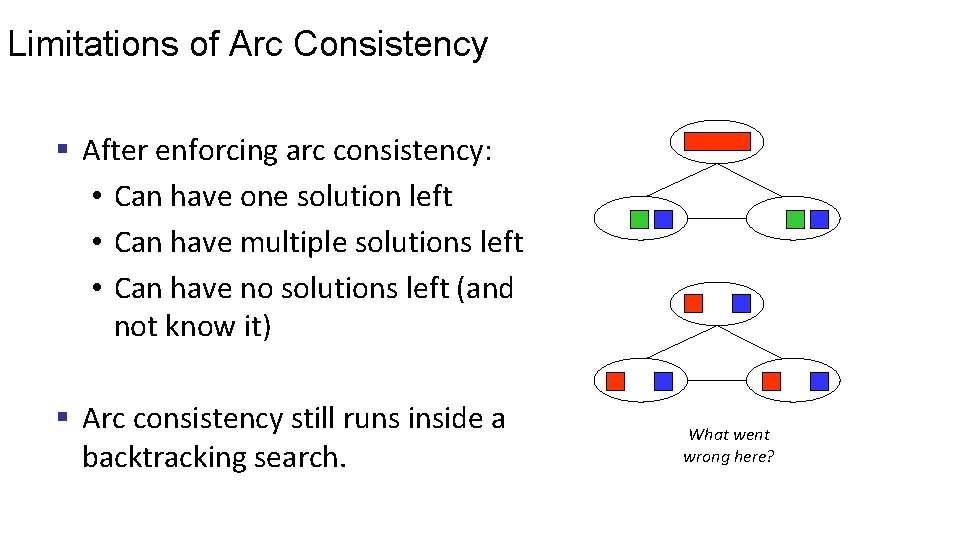
Limitations of Arc Consistency § After enforcing arc consistency: • Can have one solution left • Can have multiple solutions left • Can have no solutions left (and not know it) § Arc consistency still runs inside a backtracking search. What went wrong here?

Variable Ordering: Minimum Remaining Values § Choose the hardest variable first. § One with the fewest legal left values in its domain § Also called “most constrained variable” or “Fail-fast” ordering

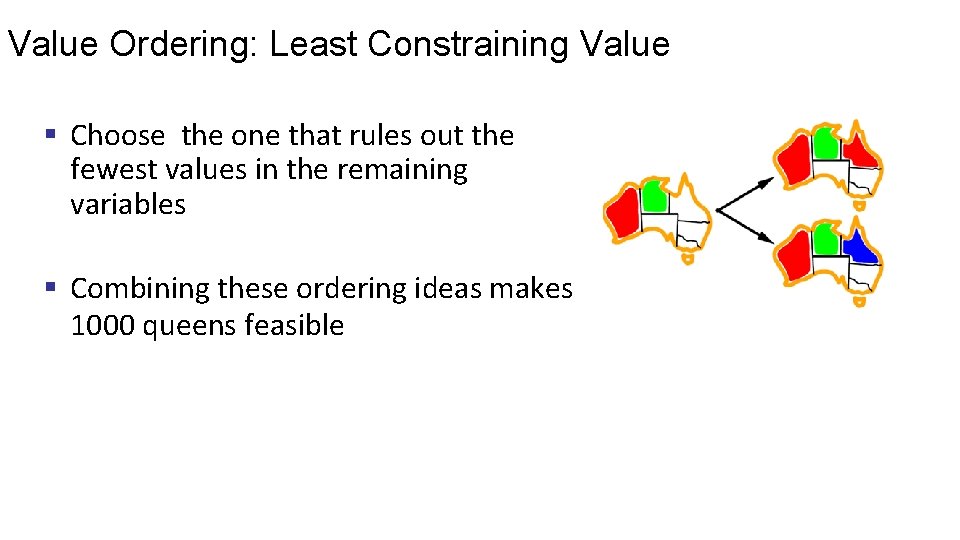
Value Ordering: Least Constraining Value § Choose the one that rules out the fewest values in the remaining variables § Combining these ordering ideas makes 1000 queens feasible

Success! We are done. inferences are pairs. Return partial assignment.

CSP backtracking search § § § § Use depth-first search. At each step, add one new variable. Check constraints as you add new variable. Backtracks when a variable has no legal values left to assign. SELECT-UNASSIGNED-VARIABLE(csp) ORDER-DOMAIN-VALUES(var, assignment, csp) INFERENCE(csp, var, value) Can solve 1000 -queens problem

Improving Backtracking § General-purpose ideas give huge gains in speed but in the end, it’s all still NP-hard § Which variable should be assigned next? § In what order should its values be tried? § Forward checking look ahead Can we detect inevitable failure early? § Can we exploit the problem structure?

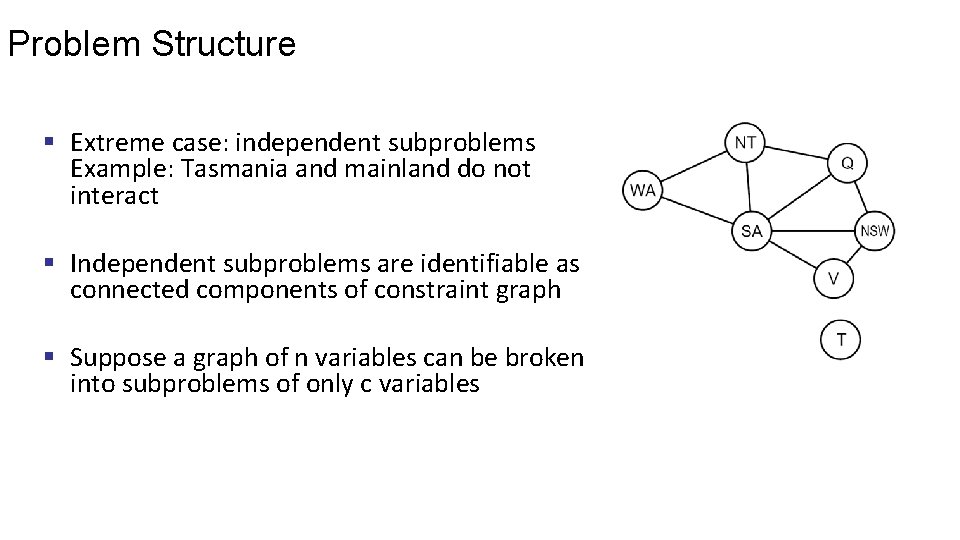
Problem Structure § Extreme case: independent subproblems Example: Tasmania and mainland do not interact § Independent subproblems are identifiable as connected components of constraint graph § Suppose a graph of n variables can be broken into subproblems of only c variables

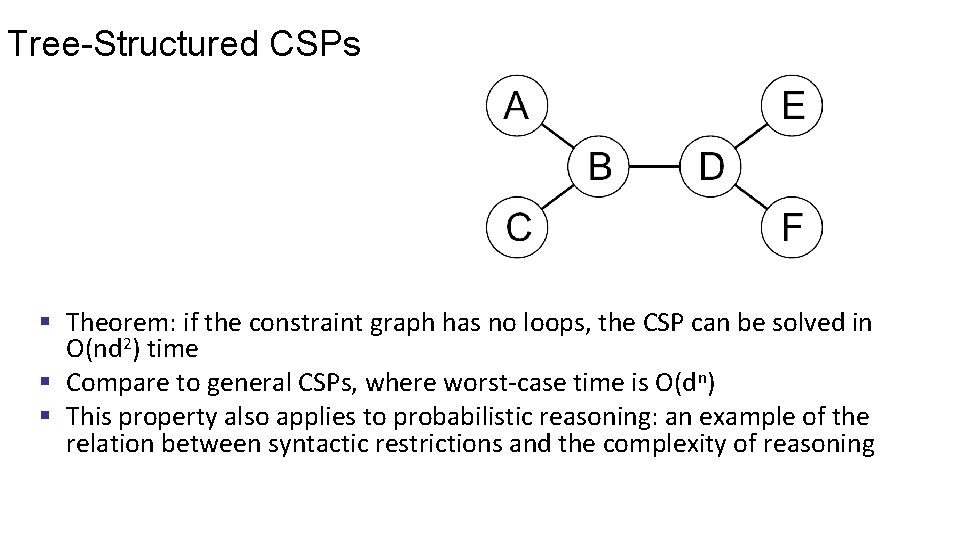
Tree-Structured CSPs § Theorem: if the constraint graph has no loops, the CSP can be solved in O(nd 2) time § Compare to general CSPs, where worst-case time is O(dn) § This property also applies to probabilistic reasoning: an example of the relation between syntactic restrictions and the complexity of reasoning

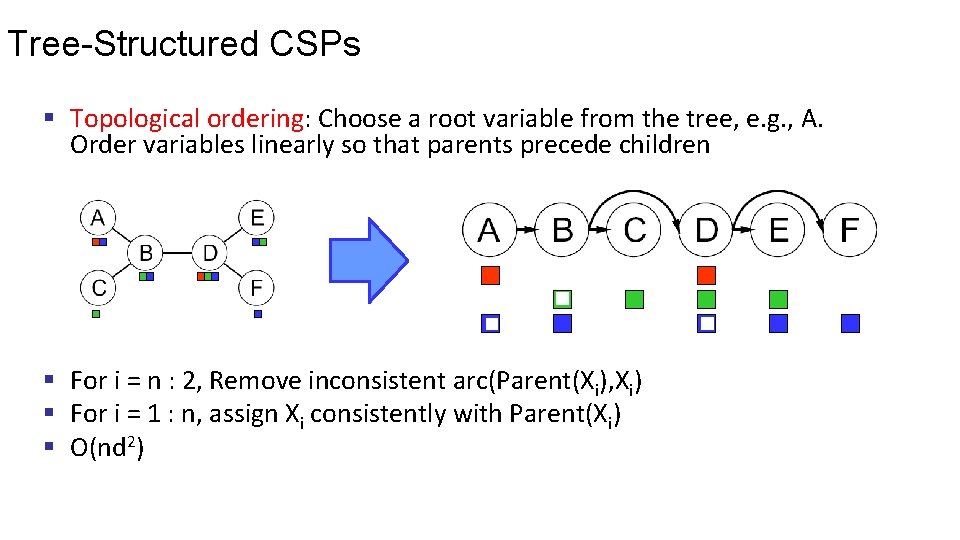
Tree-Structured CSPs § Topological ordering: Choose a root variable from the tree, e. g. , A. Order variables linearly so that parents precede children § For i = n : 2, Remove inconsistent arc(Parent(Xi), Xi) § For i = 1 : n, assign Xi consistently with Parent(Xi) § O(nd 2)

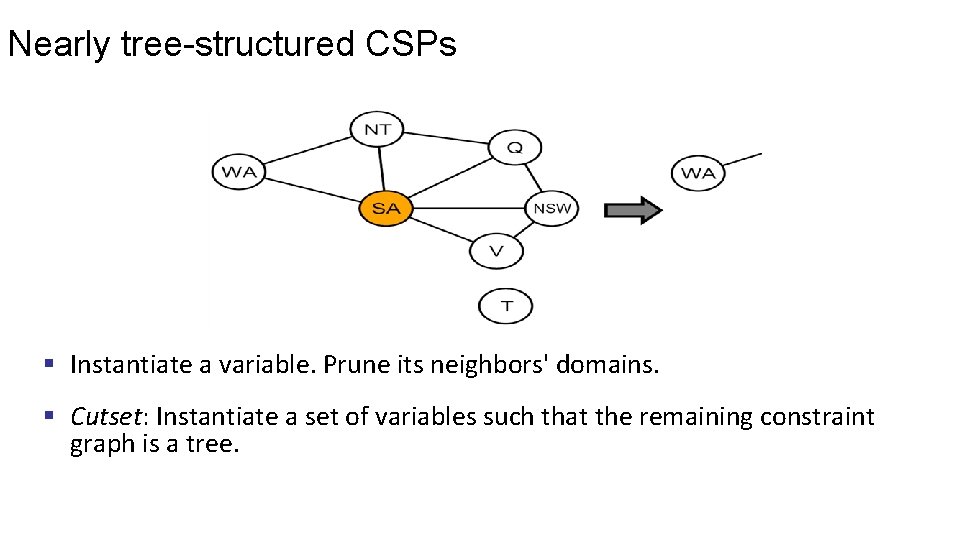
Nearly tree-structured CSPs § Instantiate a variable. Prune its neighbors' domains. § Cutset: Instantiate a set of variables such that the remaining constraint graph is a tree.

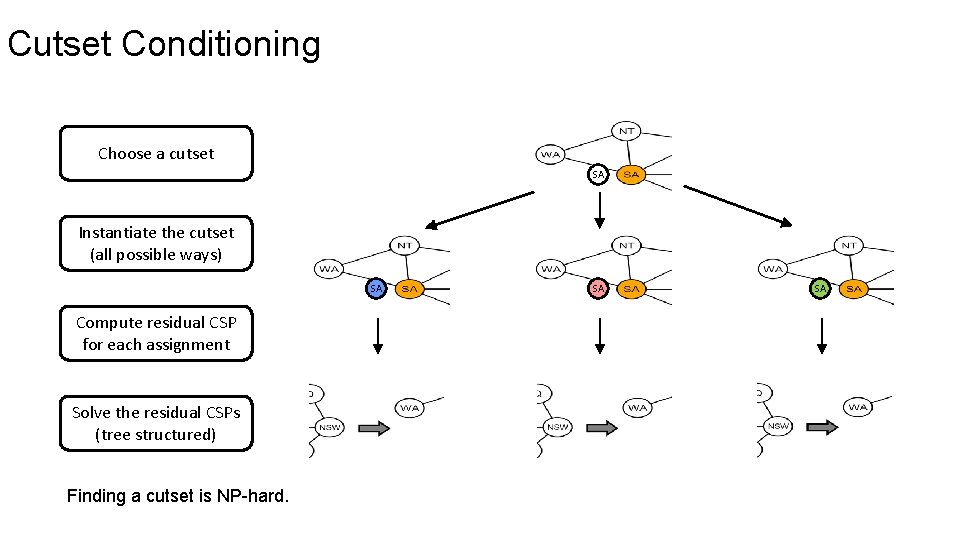
Cutset Conditioning Choose a cutset SA Instantiate the cutset (all possible ways) SA Compute residual CSP for each assignment Solve the residual CSPs (tree structured) Finding a cutset is NP-hard. SA SA

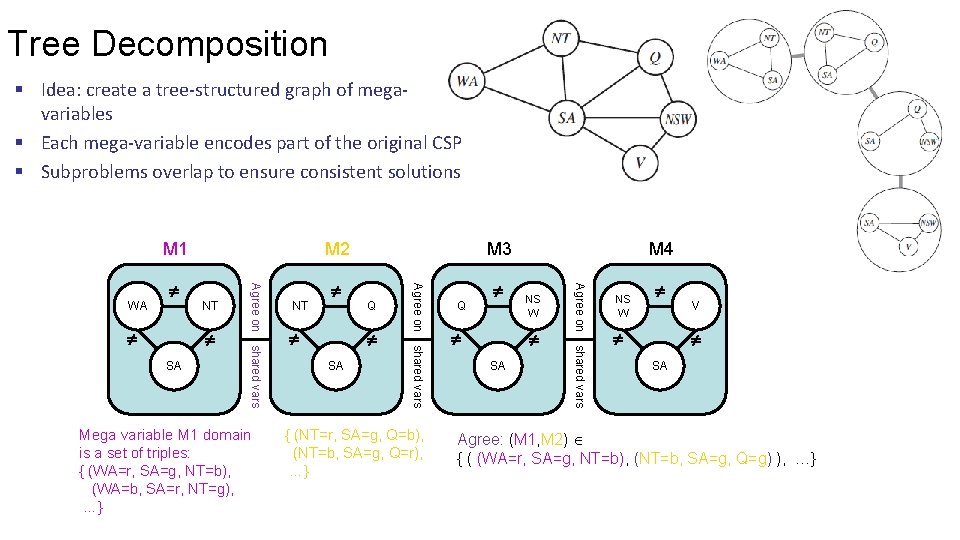
Tree Decomposition § Idea: create a tree-structured graph of megavariables § Each mega-variable encodes part of the original CSP § Subproblems overlap to ensure consistent solutions M 1 Q SA { (NT=r, SA=g, Q=b), (NT=b, SA=g, Q=r), …} Q NS W SA shared vars Mega variable M 1 domain is a set of triples: { (WA=r, SA=g, NT=b), (WA=b, SA=r, NT=g), …} M 4 Agree on SA NT shared vars NT M 3 Agree on WA M 2 NS W V SA Agree: (M 1, M 2) { ( (WA=r, SA=g, NT=b), (NT=b, SA=g, Q=g) ), …}

Iterative algorithms for CSPs § Local search methods typically work with full states, i. e. , all variables paired. § Take an assignment with unsatisfied constraints § Operators reassign variable values § No fringe! Live on the edge. § Algorithm: While not solved, • Variable selection: randomly select any conflicted variable • Value selection: min-conflicts heuristic: § Choose a value that violates the fewest constraints § I. e. , hill climb with h(n) = total number of violated constraints

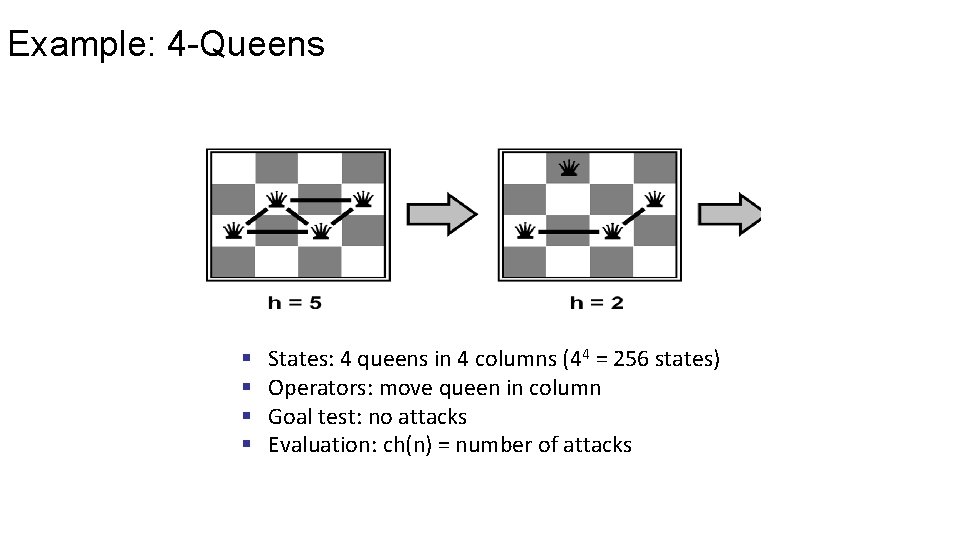
Example: 4 -Queens § § States: 4 queens in 4 columns (44 = 256 states) Operators: move queen in column Goal test: no attacks Evaluation: ch(n) = number of attacks

Local Search // Modify an instantiation in the current assignment. The heuristic CONFLICTS function counts the number of constraints violated by a particular value.

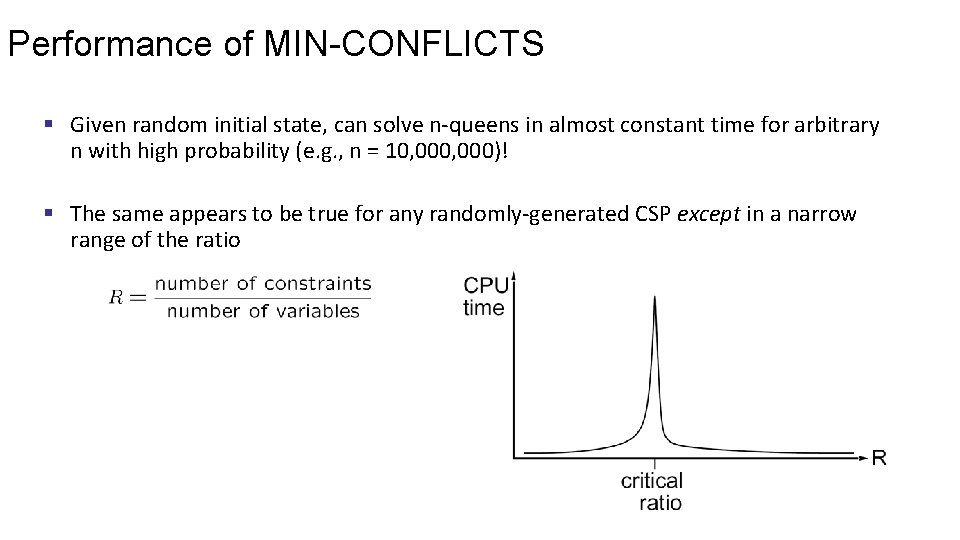
Performance of MIN-CONFLICTS § Given random initial state, can solve n-queens in almost constant time for arbitrary n with high probability (e. g. , n = 10, 000)! § The same appears to be true for any randomly-generated CSP except in a narrow range of the ratio

Summary § CSPs are a special kind of search problem States are partial assignments Goal test defined by constraints § Basic solution: backtracking search § Speed-ups: Ordering, Filtering, Structure § Iterative min-conflicts is often effective in practice § If you can formulate your problem as CSP, the program to find its solution can be generated automatically. § You don't need a human programmer to write a program to find the solution.