Constraint Programming In Pursuit of the Holy Grail

Constraint Programming: In Pursuit of the Holy Grail Roman Barták Charles University, Prague bartak@kti. mff. cuni. cz

Talk Schedule l Basic notions l Historical context l Constraint technology – constraint satisfaction – constraints optimisation – over-constrained problems l Applications l Summary – Advantages & Limitations l Trends l Resources © Roman Barták, 1999

What is CP? l CP = Constraint Programming – stating constraints about the problem variables – finding solution satisfying all the constraints l constraint = relation among several unknowns l Example: A+B=C, X>Y, N=length(S) … l Features: – – – express partial information heterogeneous non-directional declarative manner additive rarely independent © Roman Barták, 1999 X>2 N=length(S) X=Y+2: X Y+2 Y X-2 “ X>2, X<5, X>2 A+B=5, A-B=1

The Origins l Artificial Intelligence – Scene Labelling (Waltz) l Interactive Graphics – Sketchpad (Sutherland) – Thing. Lab (Borning) l Logic Programming – unification --> constraint solving l Operations Research – NP-hard combinatorial problems © Roman Barták, 1999

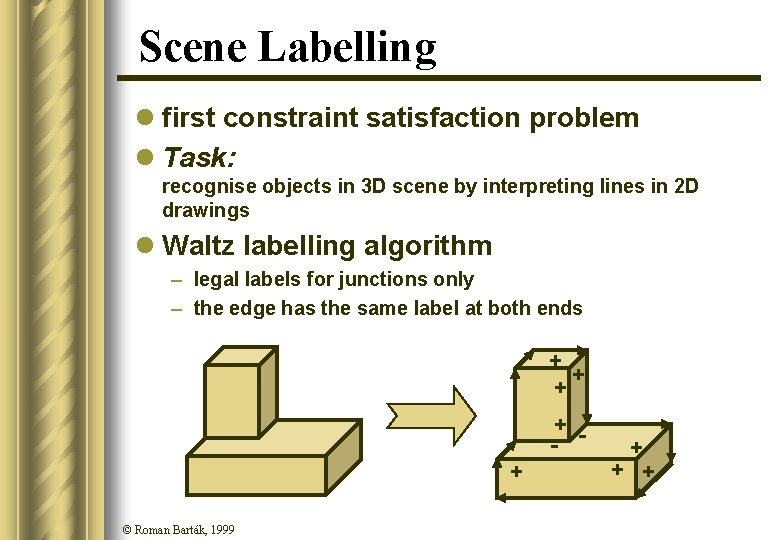
Scene Labelling l first constraint satisfaction problem l Task: recognise objects in 3 D scene by interpreting lines in 2 D drawings l Waltz labelling algorithm – legal labels for junctions only – the edge has the same label at both ends + + © Roman Barták, 1999 + - + + +

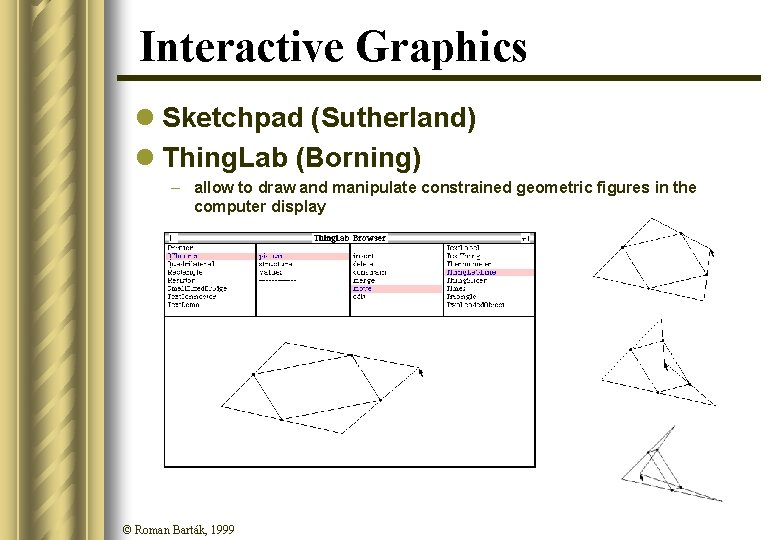
Interactive Graphics l Sketchpad (Sutherland) l Thing. Lab (Borning) – allow to draw and manipulate constrained geometric figures in the computer display © Roman Barták, 1999

Solving Technology l Constraint Satisfaction – finite domains -> combinatorial problems – 95% of all industrial applications l Constraints Solving – infinite or more complex domains – methods • automatic differentiation, Taylor series, Newton method – many mathematicians deal with whether certain constraints are satisfiable (Fermat’s Last Theorem) © Roman Barták, 1999

Constraint Satisfaction Problem l Consist of: – a set of variables X={x 1, …, xn} – variables’ domains Di (finite set of possible values) – a set of constraints Example: • X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} • X = Y, X Z, Y > Z l Solution of CSP – assignment of value from its domain to every variable satisfying all the constraints Example: • X=2, Y=2, Z=1 © Roman Barták, 1999

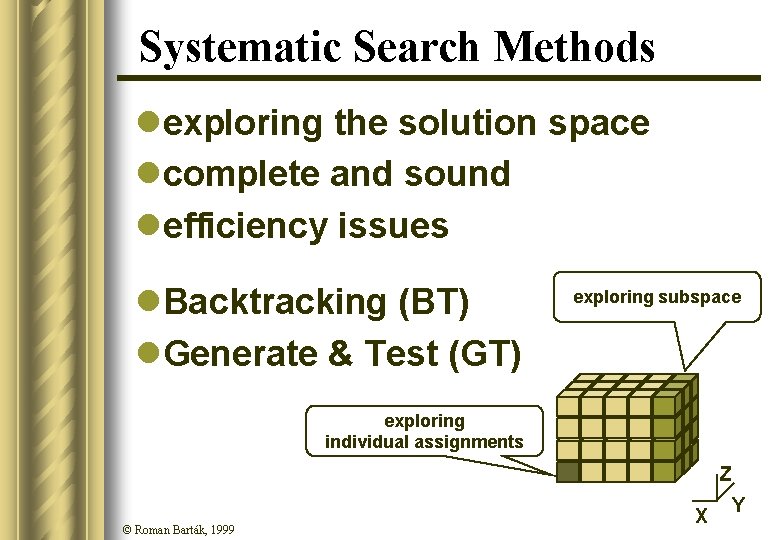
Systematic Search Methods lexploring the solution space lcomplete and sound lefficiency issues l. Backtracking (BT) l. Generate & Test (GT) exploring subspace exploring individual assignments Z © Roman Barták, 1999 X Y

Systematic Search Methods GT & BT - Example l Problem: X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X = Y, X Z, Y > Z generate & test © Roman Barták, 1999 backtracking

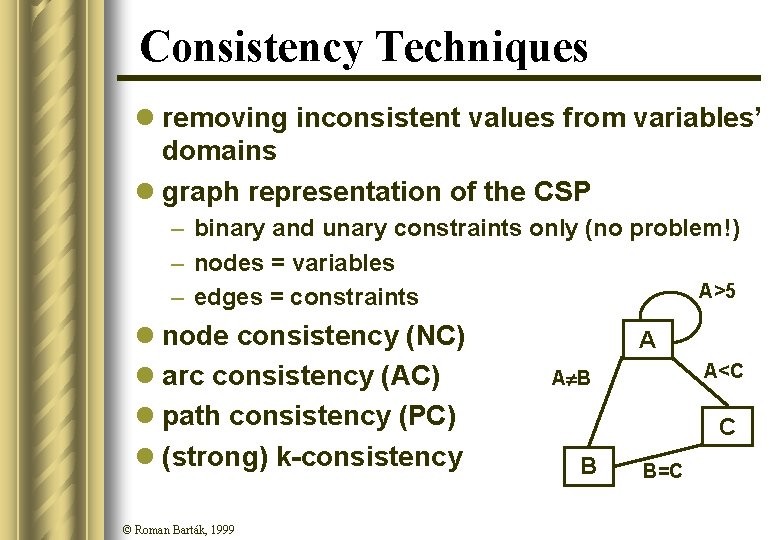
Consistency Techniques l removing inconsistent values from variables’ domains l graph representation of the CSP – binary and unary constraints only (no problem!) – nodes = variables A>5 – edges = constraints l node consistency (NC) l arc consistency (AC) l path consistency (PC) l (strong) k-consistency © Roman Barták, 1999 A A<C A B C B B=C

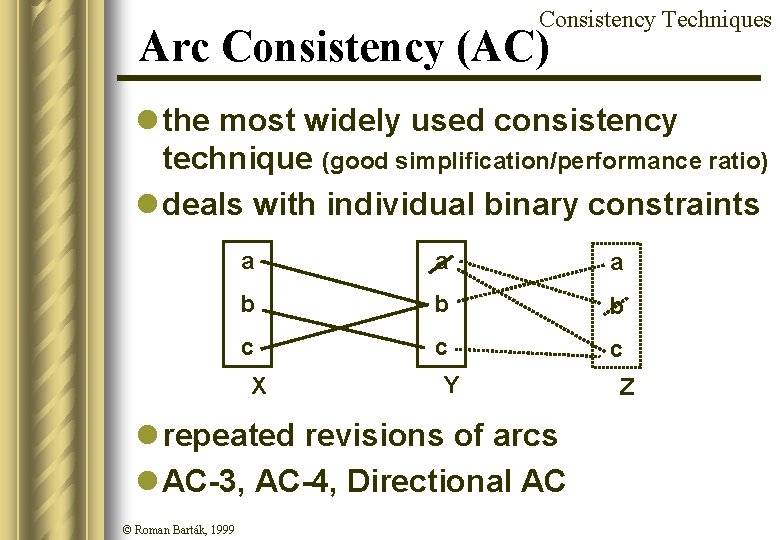
Consistency Techniques Arc Consistency (AC) l the most widely used consistency technique (good simplification/performance ratio) l deals with individual binary constraints a a a b b b c c c X Y l repeated revisions of arcs l AC-3, AC-4, Directional AC © Roman Barták, 1999 Z

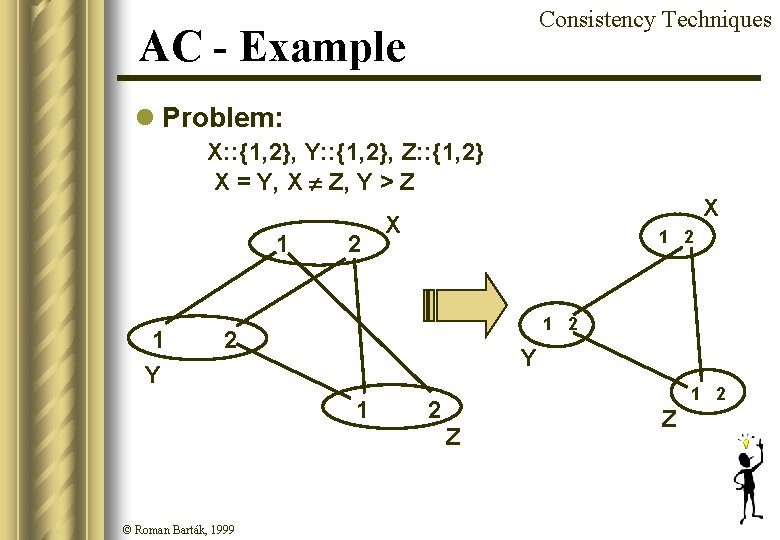
Consistency Techniques AC - Example l Problem: X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X = Y, X Z, Y > Z 1 1 Y 2 X 1 2 2 Y 1 © Roman Barták, 1999 X 2 1 2 Z Z

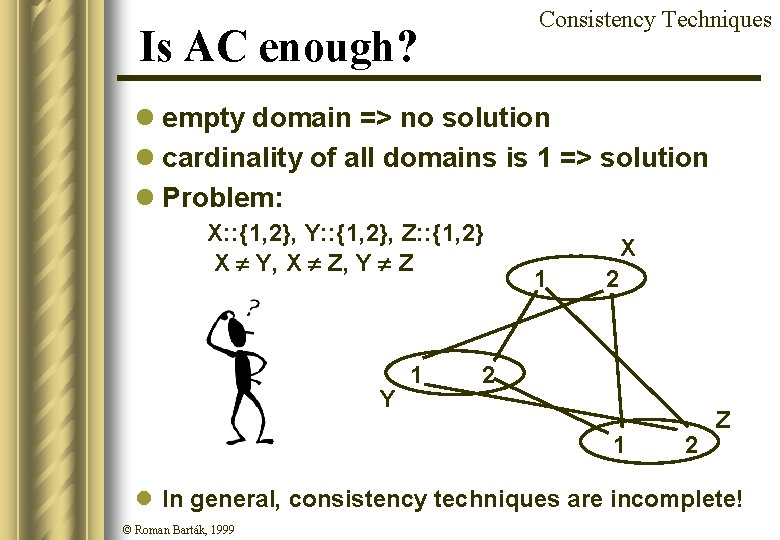
Consistency Techniques Is AC enough? l empty domain => no solution l cardinality of all domains is 1 => solution l Problem: X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X Y, X Z, Y Z Y 1 X 1 2 2 1 2 Z l In general, consistency techniques are incomplete! © Roman Barták, 1999

Constraint Propagation l systematic search only => no efficient l consistency only => no complete l Result: combination of search (backtracking) with consistency techniques l methods: – look back (restoring from conflicts) – look ahead (preventing conflicts) look back look ahead Labelling order © Roman Barták, 1999

Constraint Propagation Look Ahead - Example l Problem: X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X = Y, X Z, Y > Z generate & test - 7 steps backtracking - 5 steps propagation - 2 steps © Roman Barták, 1999

Stochastic and Heuristic Methods l GT + smart generator of complete valuations l local search - chooses best neighbouring configuration – hill climbing neighbourhood = value of one variable changed – min-conflicts neighbourhood = value of selected conflicting variable changed l avoid local minimum => noise heuristics – random-walk sometimes picks next configuration randomly – tabu search few last configurations are forbidden for next step l does not guarantee completeness © Roman Barták, 1999

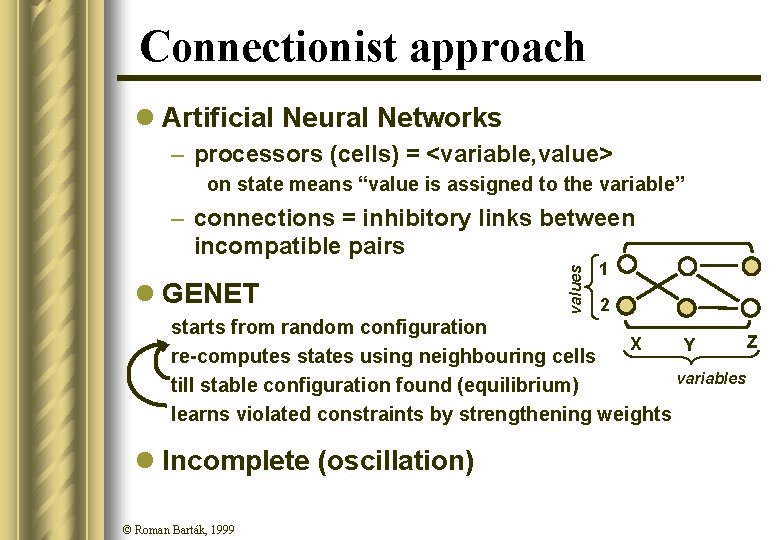
Connectionist approach l Artificial Neural Networks – processors (cells) = <variable, value> on state means “value is assigned to the variable” l GENET values – connections = inhibitory links between incompatible pairs 1 2 starts from random configuration Z X Y re-computes states using neighbouring cells variables till stable configuration found (equilibrium) learns violated constraints by strengthening weights l Incomplete (oscillation) © Roman Barták, 1999

Constraint Optimisation l looking for best solution l quality of solution measured by application dependent objective function l Constraint Satisfaction Optimisation Problem – CSP – objective function: solution -> numerical value Note: solution = complete labelling satisfying all the constraints l Branch & Bound (B&B) – the most widely used optimisation algorithm © Roman Barták, 1999

Over-Constrained Problems l What solution should be returned when no solution exists? l impossible satisfaction of all constraints because of inconsistency Example: X=5, X=4 l Solving methods – Partial CSP (PCSP) weakening original CSP – Constraint Hierarchies preferential constraints © Roman Barták, 1999

Dressing Problem Over-Constrained Problems shirt: {red, white} footwear: {cordovans, sneakers} trousers: {blue, denim, grey} shirt x trousers: red-grey, white-blue, white-denim footwear x trousers: sneakers-denim, cordovans-grey shirt x footwear: white-cordovans red white shirt blue denim grey trousers footwear cordovans sneakers © Roman Barták, 1999

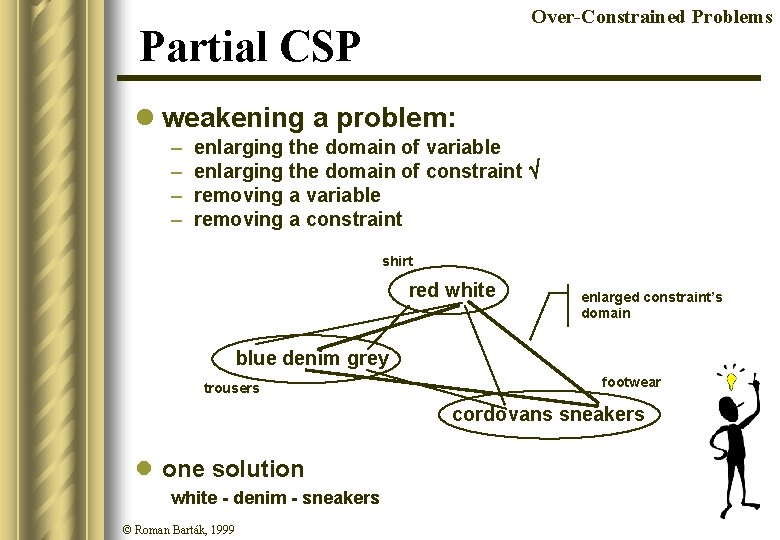
Over-Constrained Problems Partial CSP l weakening a problem: – – enlarging the domain of variable enlarging the domain of constraint removing a variable removing a constraint shirt red white enlarged constraint’s domain blue denim grey trousers footwear cordovans sneakers l one solution white - denim - sneakers © Roman Barták, 1999

Over-Constrained Problems Constraint Hierarchies l constraints with preferences l solution respects the hierarchy – weaker constraints do not cause dissatisfaction of stronger constraint l shirt x trousers @ required footwear x trousers @ strong shirt x footwear @ weak red white blue denim grey trousers footwear cordovans sneakers l two solutions red - grey - cordovans white - denim - sneakers © Roman Barták, 1999

Applications l assignment problems – stand allocation for airports – berth allocation to ships – personnel assignment • rosters for nurses • crew assignment to flights l network management and configuration – planning of cabling of telecommunication networks – optimal placement of base stations in wireless networks l molecular biology – DNA sequencing l analogue and digital circuit design © Roman Barták, 1999

Scheduling Problems l the most successful application area l l production scheduling (In. Sol Ltd. ) well-activity scheduling (Saga Petroleum) forest treatment scheduling planning production of jets (Dassault Aviation) © Roman Barták, 1999

Advantages l declarative nature – focus on describing the problem to be solved, not on specifying how to solve it l co-operative problem solving – unified framework for integration of variety of specialpurpose algorithms l semantic foundation – amazingly clean and elegant languages – roots in logic programming l applications – proven success © Roman Barták, 1999

Limitations l NP-hard problems & tracktability l unpredictable behaviour l model stability l too high-level (new constraints, solvers, heuristics) l too low-level (modelling) l too local l non-incremental (rescheduling) l weak solver collaboration © Roman Barták, 1999

Trends l modelling – global constraints (all_different) – modelling languages (Numerica, Vis. Opt) l understanding search – visualisation, performance debugging l hybrid algorithms l solver collaboration l parallelism l multi-agent technology © Roman Barták, 1999

Quotations l “Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it. ” Eugene C. Freuder, Constraints, April 1997 l “Were you to ask me which programming paradigm is likely to gain most in commercial significance over the next 5 years I’d have to pick Constraint Logic Programming, even though it’s perhaps currently one of the least known and understood. ” Dick Pountain, BYTE, February 1995 © Roman Barták, 1999

Resources l Conferences – Principles and Practice of Constraint Programming (CP) – The Practical Application of Constraint Technologies and Logic Programming (PACLP) l Journal – Constraints (Kluwer Academic Publishers) l Internet – Constraints Archive http: //www. cs. unh. edu/ccc/archive – Guide to Constraint Programming http: //kti. mff. cuni. cz/~bartak/constraints/ © Roman Barták, 1999