Constraint Networks slides courtesy of Natalia Flerova based

Constraint Networks ( slides courtesy of Natalia Flerova, based on slides courtesy of Rina Dechter)

Reading Russell and Norvig Chapter 6 (3 rd ed. ); Chapter 5 (2 nd ed. ) For next week: Chapter 7 (for Tuesday) Chapter 8 (for Thursday)

Good source of advanced information Rina Dechter, Constraint Processing, Morgan Kaufmann 3

Outline Constraint Satisfaction Problems (CSPs): Definition, and simple modeling examples Representing constraints Consistency algorithms (arc-, path- and i-consistency) General search strategy Look-ahead methods 4

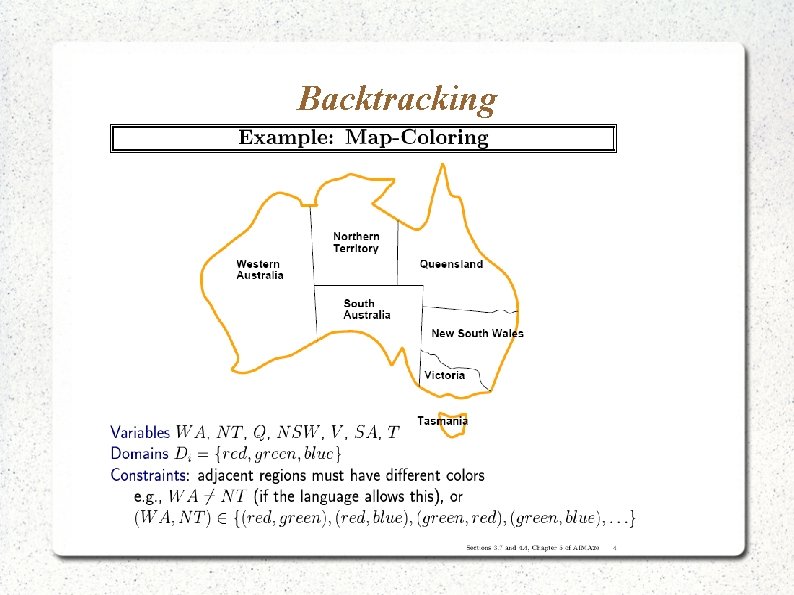
Constraint Satisfaction Example: map coloring Variables - countries (A, B, C, etc. ) Values - colors (e. g. , red, green, black) Constraints: A B red green black red black green red E A D B F C G

Constraint Network; Definition A constraint network is: R=(X, D, C) X variables D domains C constraints R expresses allowed tuples over scopes A solution is an assignment to all variables that satisfies all constraints (join of all relations). Tasks: consistency? , one or all solutions, counting, optimization 6

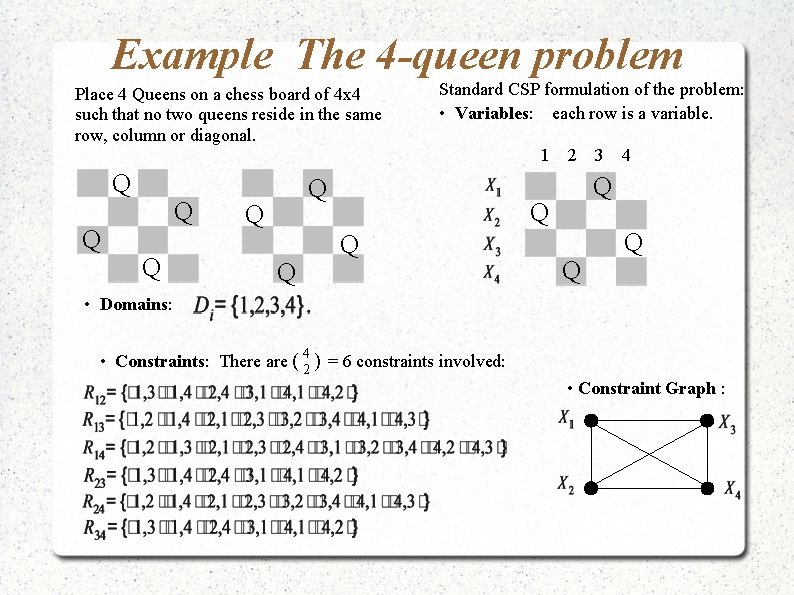
Example The 4 -queen problem Place 4 Queens on a chess board of 4 x 4 such that no two queens reside in the same row, column or diagonal. Q Q Standard CSP formulation of the problem: • Variables: each row is a variable. Q Q 2 3 4 Q Q 1 Q Q • Domains: 4 • Constraints: There are ( 2 ) = 6 constraints involved: • Constraint Graph :

Example: configuration and design Spring 2009 10

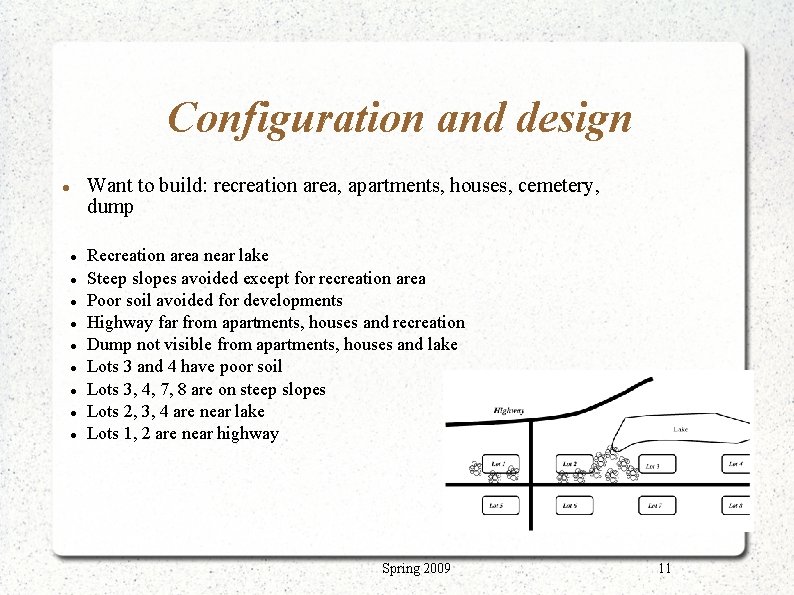
Configuration and design Want to build: recreation area, apartments, houses, cemetery, dump Recreation area near lake Steep slopes avoided except for recreation area Poor soil avoided for developments Highway far from apartments, houses and recreation Dump not visible from apartments, houses and lake Lots 3 and 4 have poor soil Lots 3, 4, 7, 8 are on steep slopes Lots 2, 3, 4 are near lake Lots 1, 2 are near highway Spring 2009 11

Outline CSP: Definition, and simple modeling examples Representing constraints Consistency algorithms (arc-, path- and i-consistency) General search strategy Look-ahead methods 12

Constraint’s representations Relation: allowed tuples Algebraic expression: Propositional formula: Spring 2009 13

Operations with relations Intersection Union Difference Selection Projection Join Composition 14

Figure 1. 8: Example of set operations intersection, union, and difference applied to relations. Spring 2009 15

selection, projection, and join operations on relations. Spring 2009 16

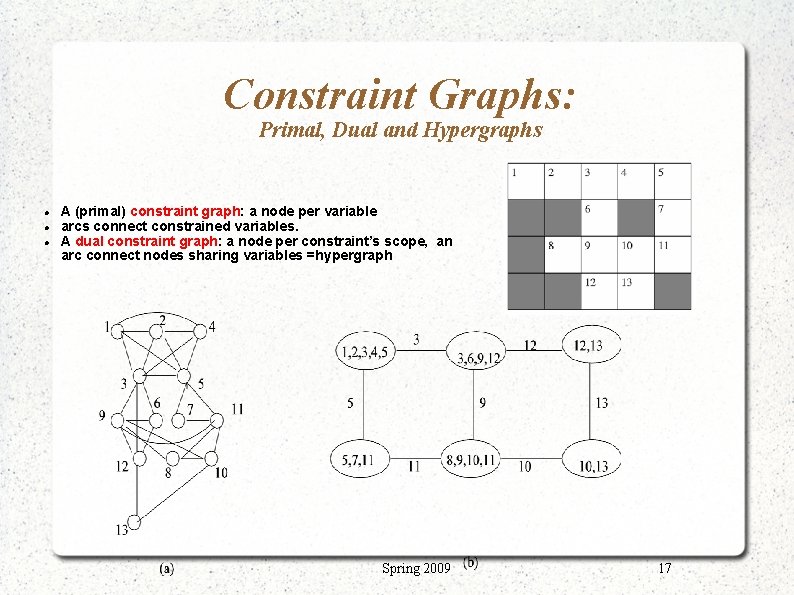
Constraint Graphs: Primal, Dual and Hypergraphs A (primal) constraint graph: a node per variable arcs connect constrained variables. A dual constraint graph: a node per constraint’s scope, an arc connect nodes sharing variables =hypergraph Spring 2009 17

Outline CSP: Definition, and simple modeling examples Representing constraints Consistency algorithms (arc-, path- and i-consistency) General search strategy Look-ahead methods 18

Consistency methods Constraint propagation – inferring new constraints Can get such an explicit network that the search will find the solution without dead-ends. Approximation of inference: Arc, path and i-consistency Methods that transform the original network into a tighter and tighter representations 19

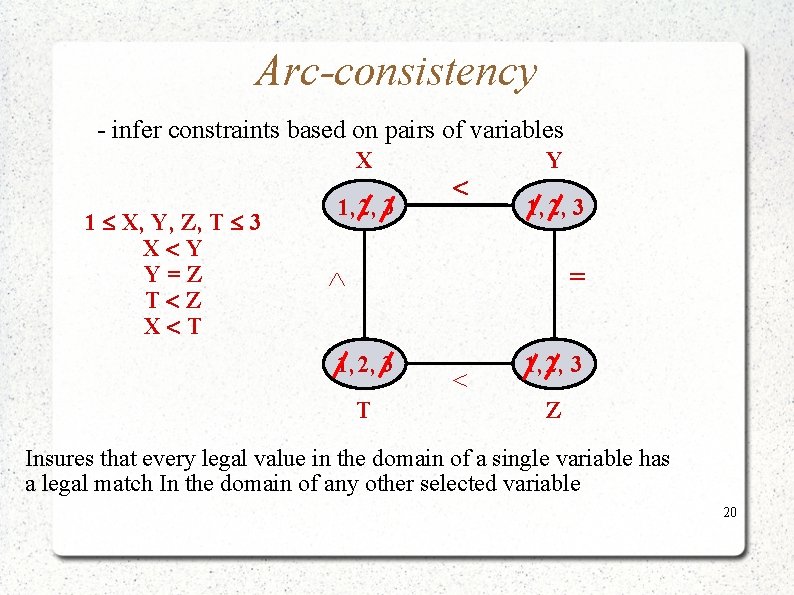
Arc-consistency - infer constraints based on pairs of variables X 1 X, Y, Z, T 3 X Y Y=Z T Z X T 1, 2, 3 Y 1, 2, 3 = 1, 2, 3 T 1, 2, 3 Z Insures that every legal value in the domain of a single variable has a legal match In the domain of any other selected variable 20

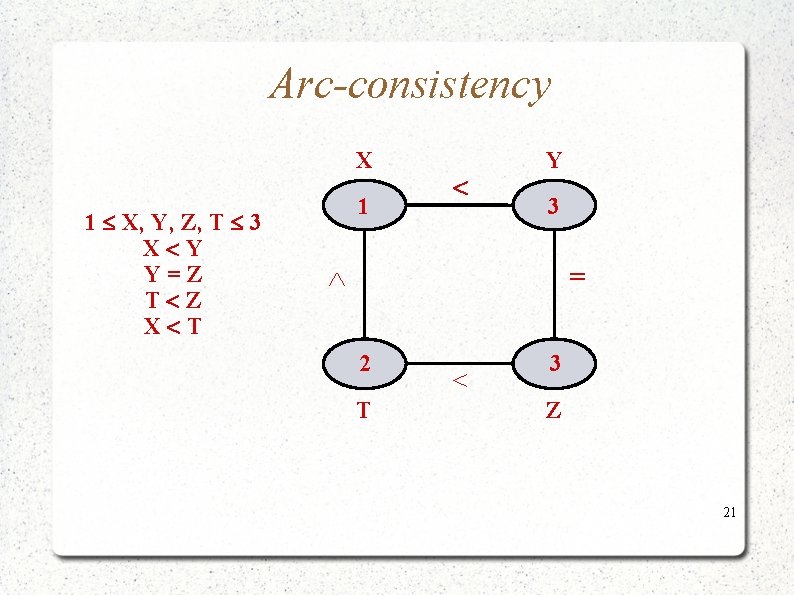
Arc-consistency X 1 X, Y, Z, T 3 X Y Y=Z T Z X T 1 Y 3 = 2 T 3 Z 21

Arc-consistency 22

Revise for arc-consistency 23

AC-1 Complexity (Mackworth and Freuder, 1986): e = number of arcs, n variables, k values (ek^2, each loop, nk number of loops), best-case = ek, Arc-consistency is: 24

AC-3 Complexity: Best case O(ek), since each arc may be processed in O(2 k) e = number of arcs, n variables, k values 25

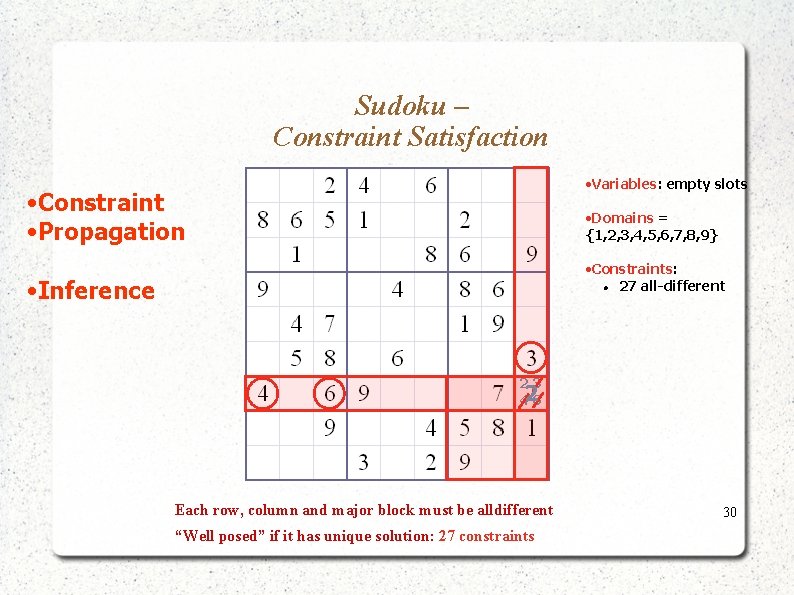
Sudoku – Constraint Satisfaction • Variables: empty slots • Constraint • Propagation • Domains = {1, 2, 3, 4, 5, 6, 7, 8, 9} • Constraints: 27 all-different • Inference 23 426 Each row, column and major block must be alldifferent “Well posed” if it has unique solution: 27 constraints 30

Path-consistency 31

Path-consistency 32

Revise-3 Complexity: O(k^3) Best-case: O(t) Worst-case O(tk) e = number of arcs, n variables, k values, t = tightness: number of tuples in the 33 constraint relation

PC-1 Complexity: e = number of arcs, n variables, k values, t = tightness: number of tuples in the constraint relation 34

PC-2 Complexity: Optimal PC-4: (each pair deleted may add: 2 n-1 triplets, number of pairs: O(n^2 k^2) size of Q is O(n^3 k^2), processing is O(k^3)) e = number of arcs, n variables, k values, t = tightness: number of tuples in the constraint relation 35

Example: before and after pathconsistency PC-1 requires 2 processings of each arc while PC-2 may not Can we do path-consistency distributedly? 36

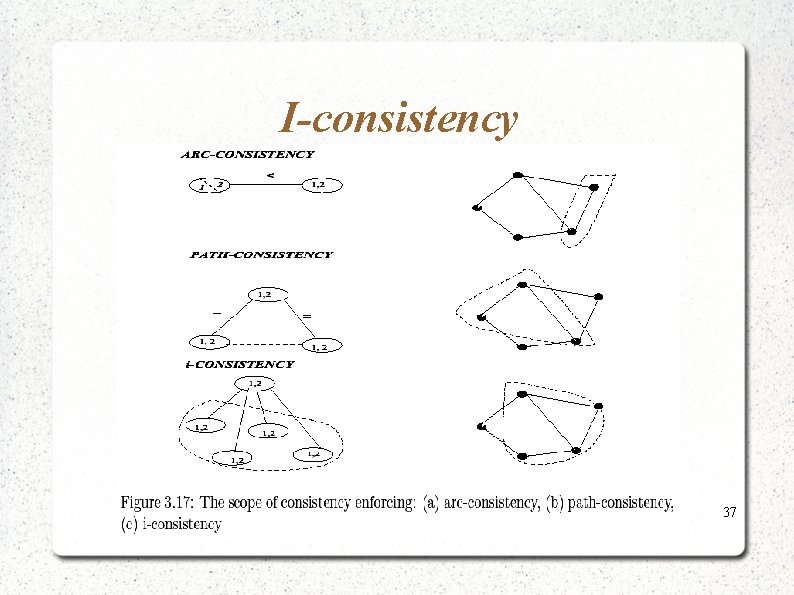
I-consistency 37

Outline CSP: Definition, and simple modeling examples Representing constraints Consistency algorithms (arc-, path- and i-consistency) General search strategy Look-ahead methods 38

Backtracking algorithm No matter how much we reason about the problem – we are still left with choices → need to search the space of possible choices. Backtracking search – assign values to each variable in turn, making sure each assigned value is consistent with values assigned thus far. Encounter variable with no domain value consistent with previous assignment – dead-end → backtrack – change the value of previous variables. 39

Backtracking

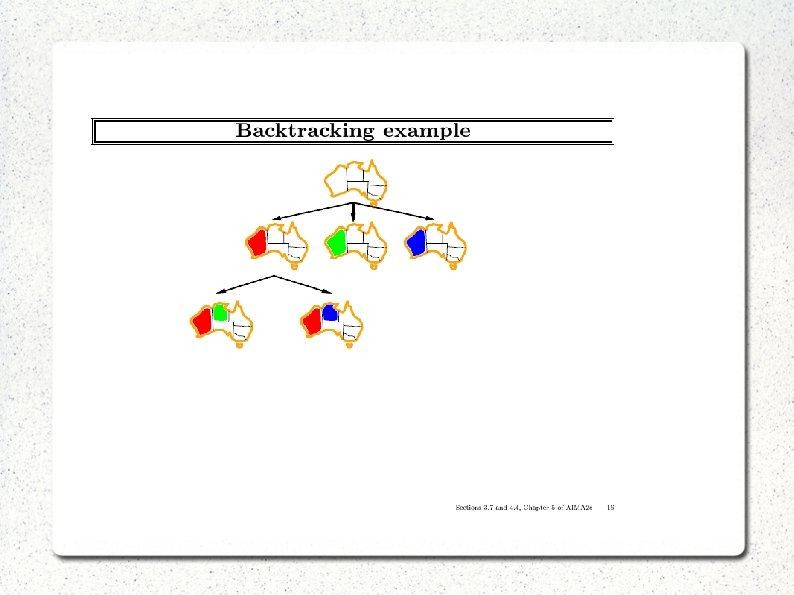
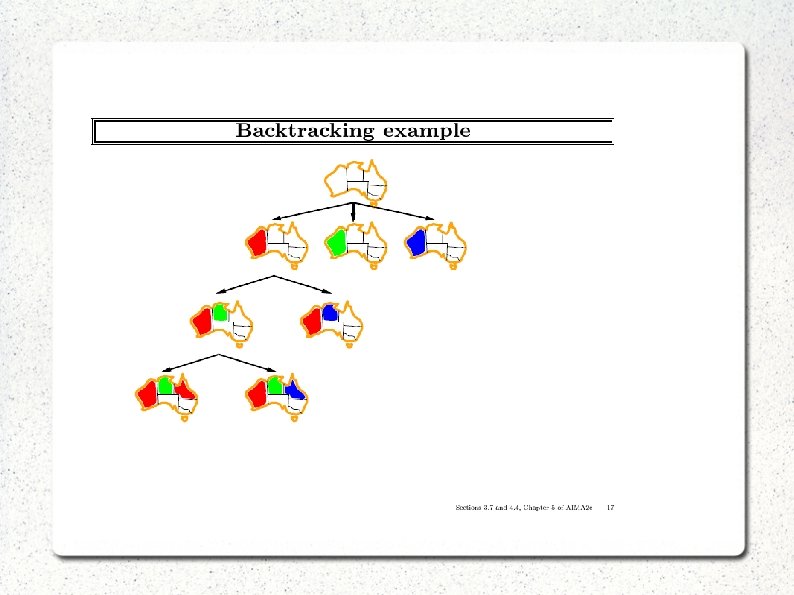
The search space A tree of all partial solutions A partial solution: (a 1, …, aj) satisfying all relevant constraints The size of the underlying search space depends on: Variable ordering Level of consistency possessed by the problem

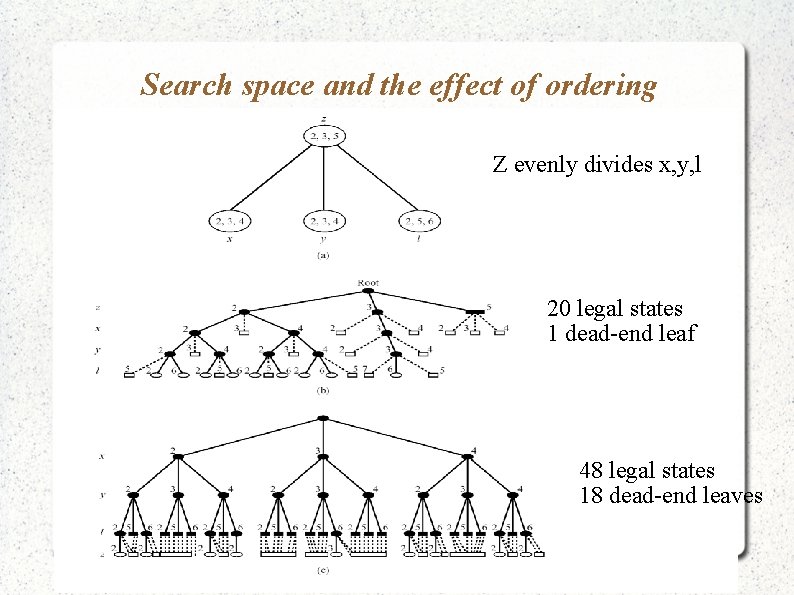
Search space and the effect of ordering Z evenly divides x, y, l 20 legal states 1 dead-end leaf 48 legal states 18 dead-end leaves

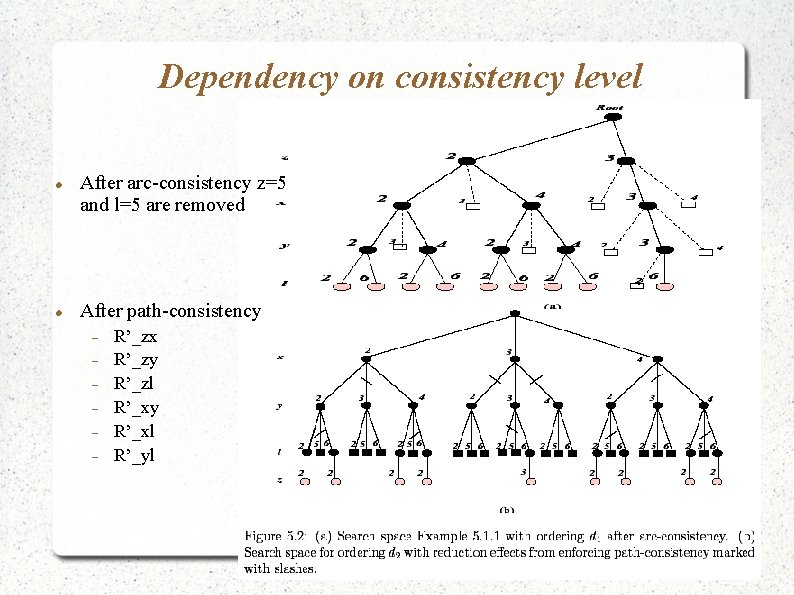
Dependency on consistency level After arc-consistency z=5 and l=5 are removed After path-consistency R’_zx R’_zy R’_zl R’_xy R’_xl R’_yl

Backtrack-free network

Backtracking Complexity of extending a partial solution: Complexity of consistent O(e log t), t bounds tuples, e constraints Complexity of selectvalue O(e k log t)

Outline CSP: Definition, and simple modeling examples Representing constraints Consistency algorithms (arc-, path- and i-consistency) General search strategy Look-ahead methods 51

Look-ahead: value orderings Intuition: Forward-checking (apply full arc-consistency) Full look-ahead (check each unassigned variable separately) Maintaining arc-consistency (MAC) Choose value least likely to yield a dead-end Approach: apply propagation at each node in the search tree One pass of arc-consistency (AC-1) Partial look-ahead directional-arc-consistency

Forward-checking The most limited form of constraint propagation during search Propagates the effect of a tentative value selection to each future variable separately If domain of one of the future variables becomes empty – value is not selected → try next value.

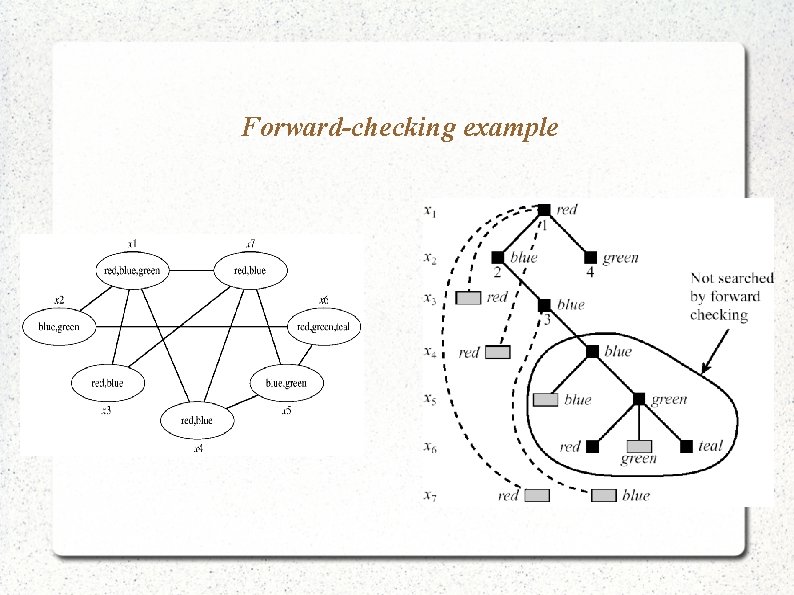
Forward-checking example

Forward-checking Complexity of select. Value-forward-checking at each node:

Arc-consistency look-ahead (Gashnig, 1977) Applies full arc-consistency on all un-instantiated variables following each value assignment to the current variable. Complexity: If optimal arc-consistency is used: Select. Value-Arc-Consistency: The repeat. . . until loop – essentially AC-1 with some variables instantiated. Maintaining-Arc-Consistency (MAC): Performs full arc-consistency after each domain value is rejected.

Arc-consistency look-ahead: (maintaining arc-consistency MAC)

Full and partial look-ahead Full looking ahead: Make one full pass through future variables (remove repeat-until from select. Value-arc-consistency) Partial look-ahead: Applies (similar-to) directional arc-consistency to future variables. - future variables are only compared with those variables following them. Complexity: also More efficient than MAC

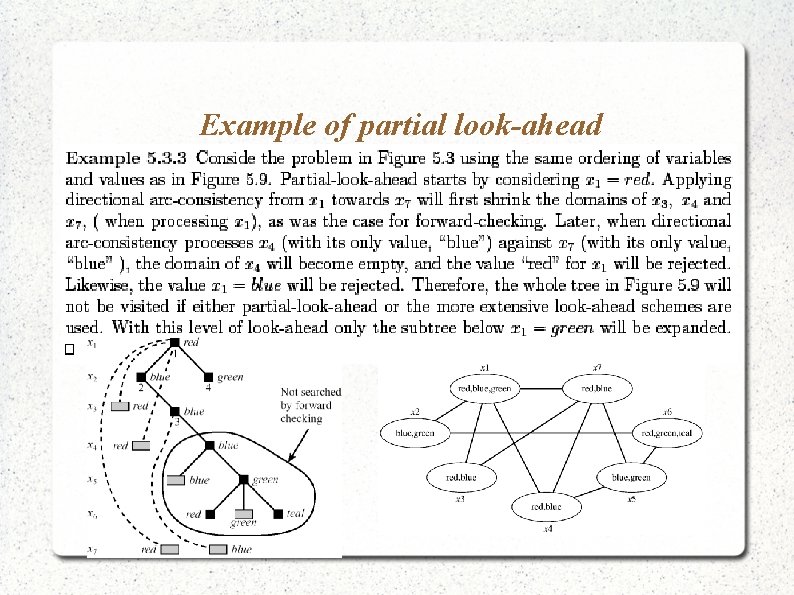
Example of partial look-ahead