Constraint Logic Programming handout Paul Y Gloess sources

Constraint Logic Programming handout Paul Y Gloess sources of inspiration include: CLP notes by Marc-Michel Corsini “Constraint Logic Programming: A Survey”, by Joxan Jaffar and Michael J. Maher, Journal of Logic Programming 1994: 19, 20: 503 -581 “Constraint Logic Programming - An Informal Introduction”, by Thom Frühwirth, Alexander Herold, Volker Küchenhoff, Thierry le Provost, Pierre Lim, Eric Monfroy, Mark Wallace, technical report ECRC-93 -5 “Constraint Logic Programming”, by Dick Fountain, Byte Magazine February 1995, © Mc Graw Hill “Algorithms for Constraint-Satisfaction Problems: A Survey”, by Vipin Kumar, AI magazine, Vol. 13, N° 1, Spring 1992: 32 -44 Journées Francophones de Programmation en Logique, La. BRI, Université Bordeaux I, 25 -27 mai 1994 CHIP V 5 Reference Manual, © Cosytec SA pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 1

Course Outline motivation for constraints deal with arithmetics or boolean domains combine efficiency and declarativeness Constraint Logic Programming CLP(X) X = rational linear constraints X = CHIP finite domains X = boolean [or CHIP boolean] X = trees LP = CLP(trees) or “pure Prolog revisited” constraint satisfiability CLP operational semantics Constraint Satisfaction Problem node and arc consistency general backtracking algorithm Generate and Test (GT) Standard Backtracking (SB) Forward Checking (FC) Look Ahead (LA) comparison on the queen example CHIP pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 2

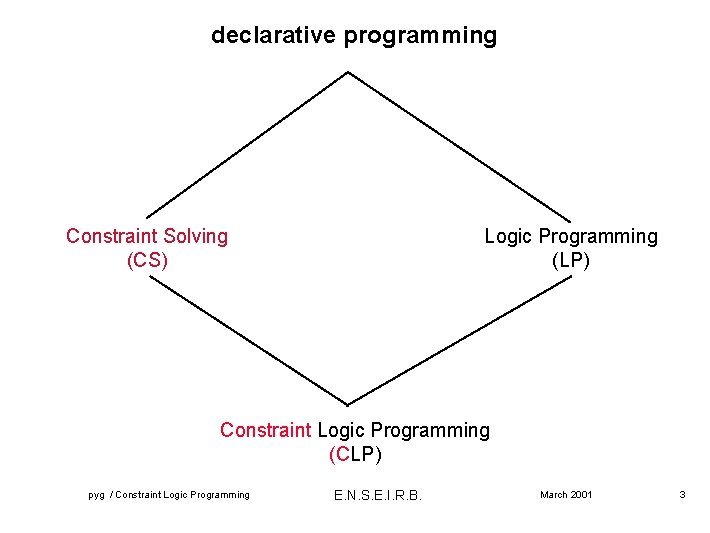
declarative programming Constraint Solving (CS) Logic Programming (LP) Constraint Logic Programming (CLP) pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 3

CLP example sumto(N, S) S=1+…+N sumto(0, 0). sumto(N, S) : - {N 1, N S}, sumto(N-1, S-N). {S 3}, sumto(N, S). sumto(N, N). {N=0, S=0}; {N=1, S=1}; {N=2, S=3}; nomore solution sumto(N+1, N); no solution! pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 4

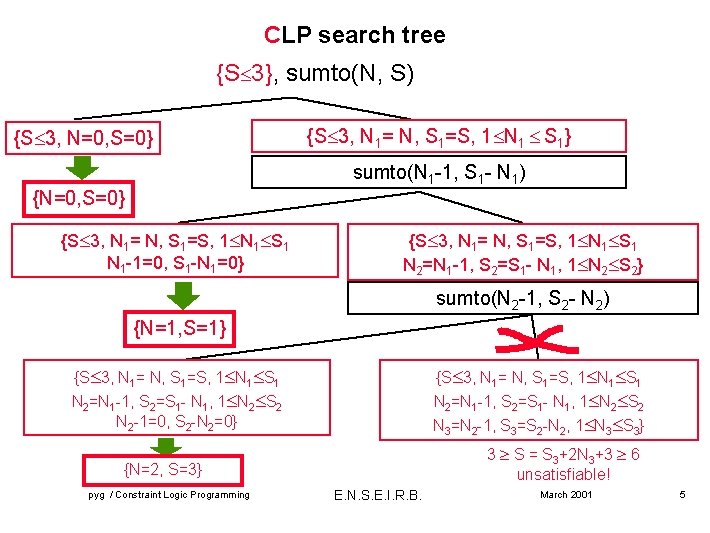
CLP search tree {S 3}, sumto(N, S) {S 3, N=0, S=0} {S 3, N 1= N, S 1=S, 1 N 1 S 1} sumto(N 1 -1, S 1 - N 1) {N=0, S=0} {S 3, N 1= N, S 1=S, 1 N 1 S 1 N 1 -1=0, S 1 -N 1=0} {S 3, N 1= N, S 1=S, 1 N 1 S 1 N 2=N 1 -1, S 2=S 1 - N 1, 1 N 2 S 2} sumto(N 2 -1, S 2 - N 2) {N=1, S=1} {S 3, N 1= N, S 1=S, 1 N 1 S 1 N 2=N 1 -1, S 2=S 1 - N 1, 1 N 2 S 2 N 2 -1=0, S 2 -N 2=0} {S 3, N 1= N, S 1=S, 1 N 1 S 1 N 2=N 1 -1, S 2=S 1 - N 1, 1 N 2 S 2 N 3=N 2 -1, S 3=S 2 -N 2, 1 N 3 S 3} 3 S = S 3+2 N 3+3 6 unsatisfiable! {N=2, S=3} pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 5

LP power versus CLP power LP add(0, N, N). add(s(M), N, s(MN)) : - add(M, N, MN). add(M, N, K), add(M, N, s(K)). … loop for ever or stack overflow CLP {M+N=K, M+N=K+1}. no solution! pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 6

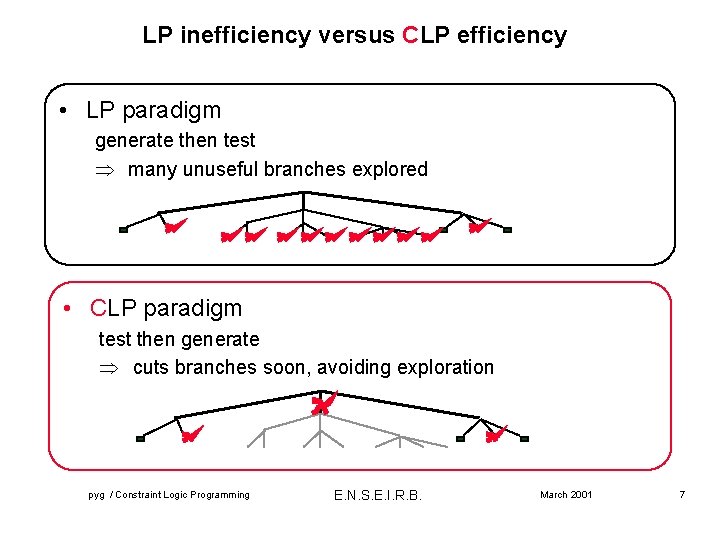
LP inefficiency versus CLP efficiency • LP paradigm generate then test many unuseful branches explored • CLP paradigm test then generate cuts branches soon, avoiding exploration pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 7

CLP operational semantics inference rules pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 8

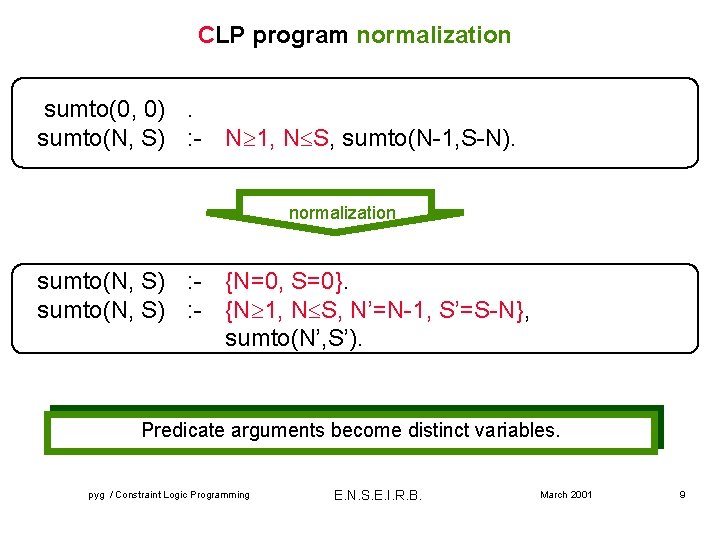
CLP program normalization sumto(0, 0). sumto(N, S) : - N 1, N S, sumto(N-1, S-N). normalization sumto(N, S) : - {N=0, S=0}. sumto(N, S) : - {N 1, N S, N’=N-1, S’=S-N}, sumto(N’, S’). Predicate arguments become distinct variables. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 9

CLP(X) • A basis B= F, P for constraints • P: predicate symbols containing equality “=”; • F: function symbols. • A constraint language (a set of B-atoms). • A B-semantics I of domain D with • f. I : Dn D, for each f in Fn; • p. I : Dn Bool, for each p in Pn; • =I : D D Bool is “mathematical equality”. An additional set LP of symbols is available to the user for defining predicates: symbols in LP are “uninterpreted”, have no semantics. [No uninterpreted function symbols are necessary, owing to normalization. ] pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 10

Constraint Satisfaction main CLP(X) issue BX, LX, IX constraint[s] in LX X |= C read: C is satisfiable in X by definition IX |= C where: C is the existential closure of C pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 11

CLP(Qlin) rational linear constraints • Constraint basis B= F, P with • P = {=, <, , >, }; • F = {+, -, -1, *, /} Q • Constraint language (linear arithmetics): • X+3*Y > 50*Z - (3/4)*Y • X*Y 3 not allowed (not linear) • X/5 > Y/2 division by numbers OK • X/Y = Z not allowed • B-semantics I of domain Q with classical interpretation of predicate and function symbols. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 12

CLP(FD) CHIP Finite Domains • Constraint basis B= F, P with • P = {=, <, , >, , } {in[m, n] | m n, m, n Nat} • F = {+, *} Nat • Constraint language (linear integer arithmetics with each variable ranging in a finite domain): • {X [1, 5], Y [0, 7], X 3, X+2*Y 5, X+Y 9} • B-semantics I of domain Nat. Z interprets arithmetic operators and comparators as usual. The constraint X [m, n] is understood as m X n. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 13

CLP(Boolean) boolean constraints • Constraint basis B= F, P with • P = {=}; • F = {true, false, , , }. • Constraint language (boolean constraints): • ((X Y) X) = (Y Z) • (X Y) = true • B-semantics I of domain Bool={true, false} with usual interpretation of boolean symbols. Remark: since the domain of I is Bool, it is possible to let all boolean operators (symbols in F) belong to P as well. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 14

CLP(CHIP Boolean) CHIP boolean constraints CHIP extends boolean constraints to arbitrary symbolic constants other than true and false. These constants are implicitely universally quantified. Example: ((X drunk) alcoholic) = (X drunk) Satisfiability of this constraint is defined by: Boolean |= X D A ((X D) A) = (X D) pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 15

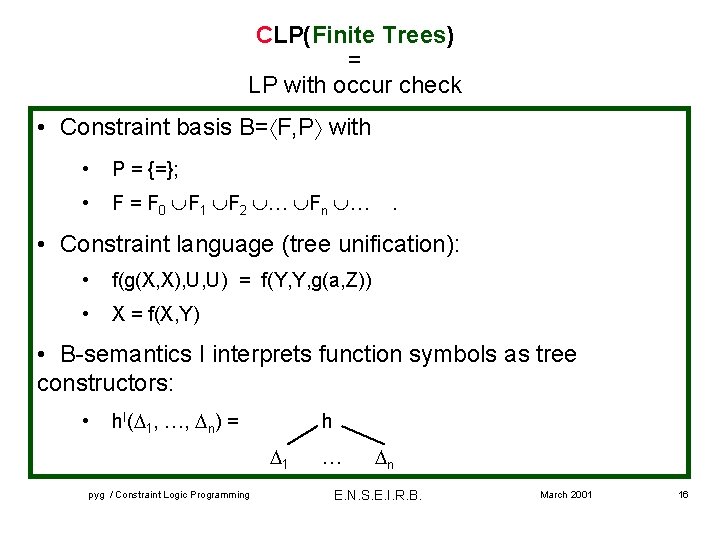
CLP(Finite Trees) = LP with occur check • Constraint basis B= F, P with • P = {=}; • F = F 0 F 1 F 2 … Fn … . • Constraint language (tree unification): • f(g(X, X), U, U) = f(Y, Y, g(a, Z)) • X = f(X, Y) • B-semantics I interprets function symbols as tree constructors: • h. I( 1, …, n) = h 1 pyg / Constraint Logic Programming … n E. N. S. E. I. R. B. March 2001 16

CLP(Finitely Branched Regular Trees) = LP with no occur check • Finite trees are replaced with finitely branched regular trees: • A (possibly infinite) tree is finitely branched if each node has a finite number of successors; • A (possibly infinite) tree is regular if it has a finite number of subtrees. • Constraint language is the same: • f(g(X, X), U, U) = f(Y, Y, g(a, Z)) • X = f(X, Y) becomes satisfiable! • B-semantics I also interprets function symbols as tree constructors. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 17

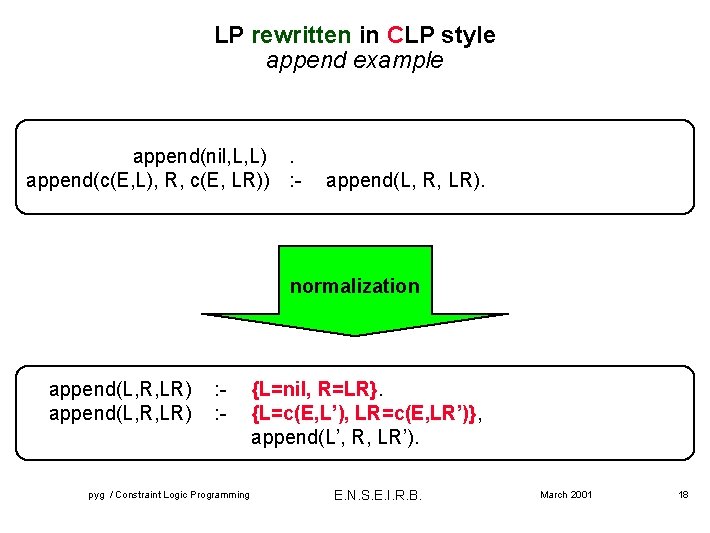
LP rewritten in CLP style append example append(nil, L, L). append(c(E, L), R, c(E, LR)) : - append(L, R, LR). normalization append(L, R, LR) : : - pyg / Constraint Logic Programming {L=nil, R=LR}. {L=c(E, L’), LR=c(E, LR’)}, append(L’, R, LR’). E. N. S. E. I. R. B. March 2001 18

Constraint Satisfaction in X • Constraint language must be decidable: – existence of algorithm for deciding whether X |= C holds or not • Decision algorithm must be efficient: – polynomial or linear on the average; – better: polynomial or linear in the worst case. • Decision algorithm better be incremental: – inference adds new constraints to a satisfiable set: algorithm should just test compatibility of the new ones with the old ones, not test satisfiability of whole set. • Compromises are possible: – admit constraint languages (e. g. , non linear constraints) with no algorithm; – wait until constraints become decidable (e. g. , linear) by further instantiation of variables. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 19

Delaying non linear Constraints mult([R 1, I 1], [R 2, I 2], [R, I]) : - R = R 1*R 2 - I 1*I 2, I = R 1*I 2 + I 1*R 2. complex multiplication mult([1, 2], [3, 4], [R, I]); {R=-5, I=10}; nomore solution mult([1, 2], [X, Y], [A, B]); {A=X-2*Y, B=Y+2*X}; nomore solution mult([R 1, 2], [R 2, 4], [-5, 10]); {R 1=-0. 5*R 2+2. 5, 3=R 1*R 2} maybe; nomore solution mult([R 1, 2], [R 2, 4], [-5, 10]), (R 1 =1; R 1 =2; R 1 =3); {R 1 =1, R 2=3}; nomore solution pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 20

k-Consistency Techniques • Goal: – speed up constraint solving. • Assumptions: – each variable ranges in a domain (usually finite); – any kind of constraints. • Method: – try to narrow variable domains by detecting inconsistencies among domains of variable subsets of size k; – propagate information about variables until domains become stable (cannot be reduced). • Advantages and drawbacks: – efficient in practice; – very general: not specific of a kind of constraints (works even without a satisfiability decision procedure); – not complete: no guarantee to detect unsatisfiability of the constraints until all variables are instantiated. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 21

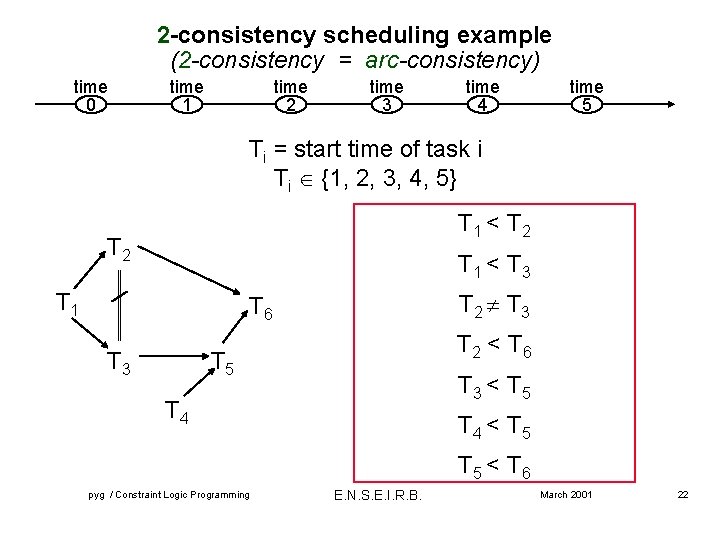
2 -consistency scheduling example (2 -consistency = arc-consistency) time 0 time 1 time 2 time 3 time 4 time 5 Ti = start time of task i Ti {1, 2, 3, 4, 5} T 1 < T 2 T 1 < T 3 T 1 T 2 T 3 T 6 T 3 T 2 < T 6 T 5 T 3 < T 5 T 4 < T 5 < T 6 pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 22

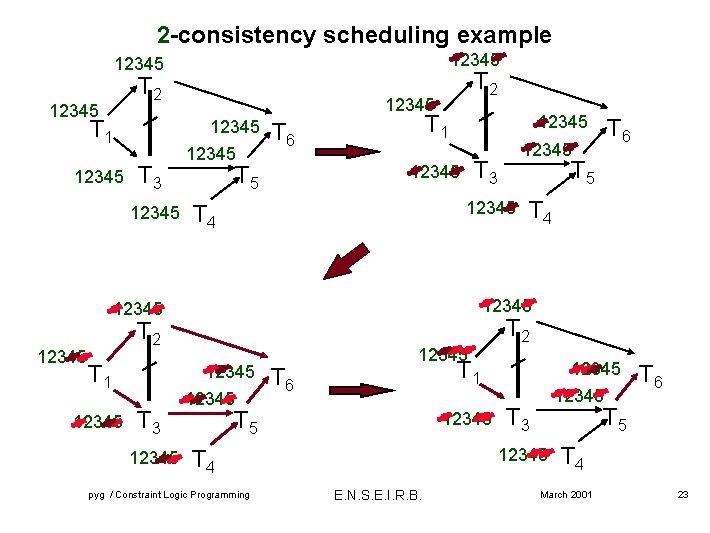
2 -consistency scheduling example 12345 T 2 12345 T 1 12345 T 3 12345 T 2 12345 T 1 T 6 T 5 12345 T 3 12345 T 4 12345 T 2 T 1 T 5 12345 T 4 12345 T 6 12345 T 1 T 5 12345 T 3 E. N. S. E. I. R. B. T 6 T 5 12345 T 4 pyg / Constraint Logic Programming 12345 T 4 March 2001 23

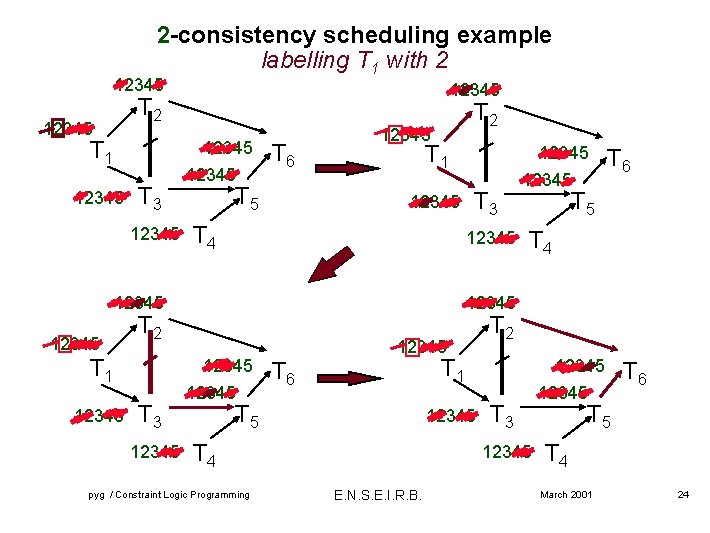
2 -consistency scheduling example labelling T 1 with 2 12345 T 1 12345 T 3 12345 T 6 T 5 T 2 12345 T 1 12345 T 4 12345 T 3 12345 T 6 T 5 T 4 12345 T 2 T 1 T 3 12345 12345 T 1 T 6 T 5 12345 T 4 pyg / Constraint Logic Programming T 2 T 3 12345 E. N. S. E. I. R. B. 12345 T 6 T 5 T 4 March 2001 24

General Backtracking Algorithm for solving a binary CSP Given problem variables X 1, …, Xi, …, Xj, …, Xn ; with domains D 1, …, Di, …, Dj, …, Dn ; problem constraints Ci, j(Xi, Xj), for 1 i<j n ; Result an enumeration of all valuations {X 1=d 1, …, Xn=dn} such that d 1 D 1 , …, dn Dn Ci, j(di, dj) = true, for 1 i<j n. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 25

General Backtracking Algorithm for solving a binary CSP (idea) Incrementally build valuation extend {X 1=d 1, …, Xk=dk} , into {X 1=d 1, …, Xk=dk, Xk+1=dk+1}, by choosing dk+1 Dk+1 , when 0 k<n, so that some adequate criterion is satisfied, and then narrow the remaining domains Dk+2 , …, Dn accordingly. Output valuation when it is complete (k=n) [it must be a solution!]. Go back when 0<k<n but valuation cannot be extended. Stop when cannot go back anymore (k=0). pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 26

Choice of dk+1: Adequate Criteria • Generate and Test (GT): – when k<n-1, do not consider constraints; – when k=n-1, restrict choice of dn so that the extended valuation {X 1=d 1, …, Xn=dn} satisfies all constraints. + most inefficient strategy! • Standard Backtracking (SB): – restrict choice of dk+1 so that newly extended valuation {X 1=d 1, …, Xk+1=dk+1} satisfies constraints so far: • Ci, j(di, dj) = true, for 1 i<j k+1. • Forward Checking (FC): – in addition to SB restriction, choose dk+1 so that: • C 1, (d 1, X ) … Ck+1, (dk+1, X ) is satisfiable for k+1< n. • Look Ahead (LA): – in addition to FC restriction, check satisfiability of: • Ck+2, (Xk+2, X ) … C -1, (X -1, X ) C , +1(X , X +1) C , n(X , Xn), for k+1< <n. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 27

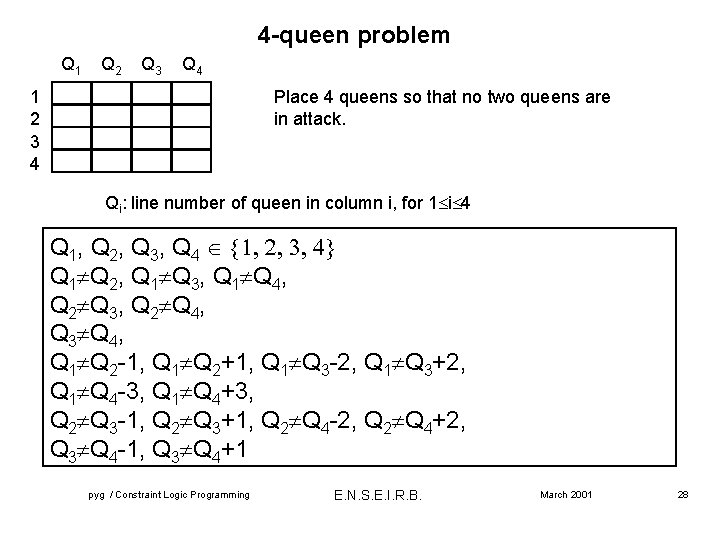
4 -queen problem Q 1 Q 2 Q 3 Q 4 1 2 3 4 Place 4 queens so that no two queens are in attack. Qi: line number of queen in column i, for 1 i 4 Q 1, Q 2, Q 3, Q 4 Q 1 Q 2, Q 1 Q 3, Q 1 Q 4, Q 2 Q 3, Q 2 Q 4, Q 3 Q 4, Q 1 Q 2 -1, Q 1 Q 2+1, Q 1 Q 3 -2, Q 1 Q 3+2, Q 1 Q 4 -3, Q 1 Q 4+3, Q 2 Q 3 -1, Q 2 Q 3+1, Q 2 Q 4 -2, Q 2 Q 4+2, Q 3 Q 4 -1, Q 3 Q 4+1 pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 28

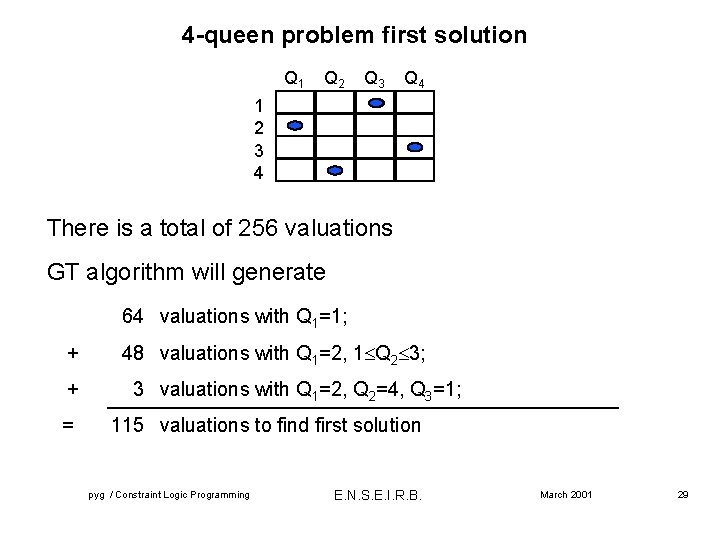
4 -queen problem first solution Q 1 Q 2 Q 3 Q 4 1 2 3 4 There is a total of 256 valuations GT algorithm will generate 64 valuations with Q 1=1; + + = 48 valuations with Q 1=2, 1 Q 2 3; 3 valuations with Q 1=2, Q 2=4, Q 3=1; 115 valuations to find first solution pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 29

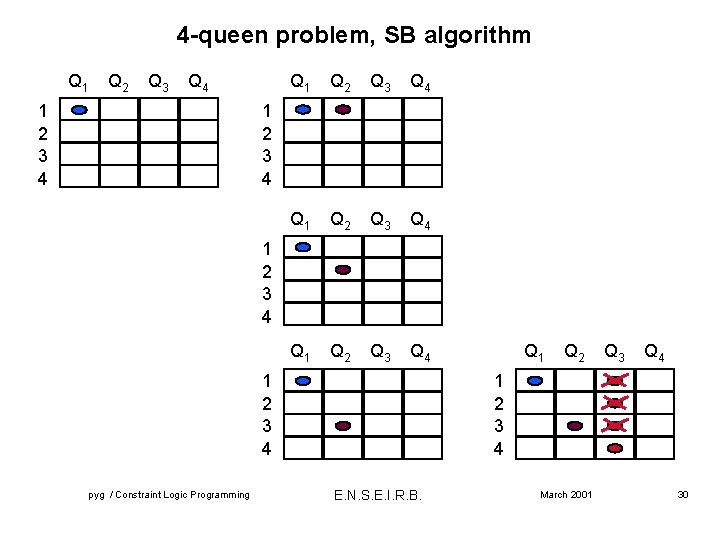
4 -queen problem, SB algorithm Q 1 Q 2 Q 3 Q 4 1 2 3 4 Q 1 Q 2 Q 3 Q 4 1 2 3 4 pyg / Constraint Logic Programming Q 1 Q 2 Q 3 Q 4 1 2 3 4 E. N. S. E. I. R. B. March 2001 30

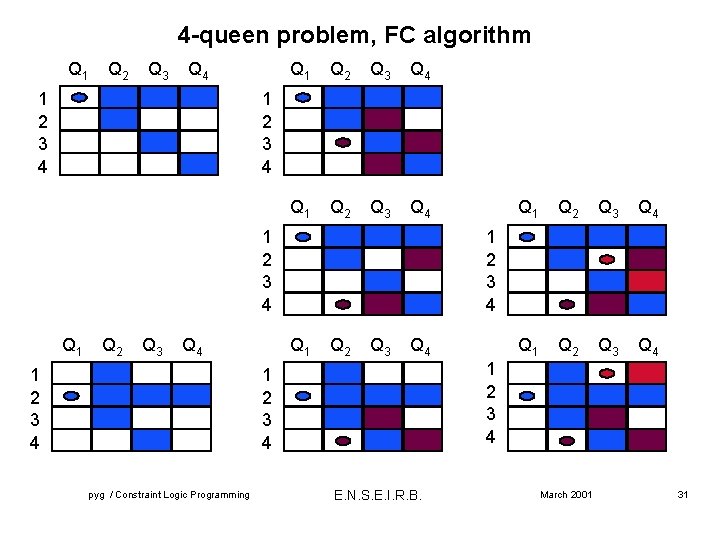
4 -queen problem, FC algorithm Q 1 Q 2 Q 3 Q 4 1 2 3 4 Q 1 Q 2 Q 3 Q 4 1 2 3 4 Q 2 Q 3 Q 4 Q 1 Q 2 Q 3 Q 4 1 2 3 4 pyg / Constraint Logic Programming Q 1 E. N. S. E. I. R. B. March 2001 31

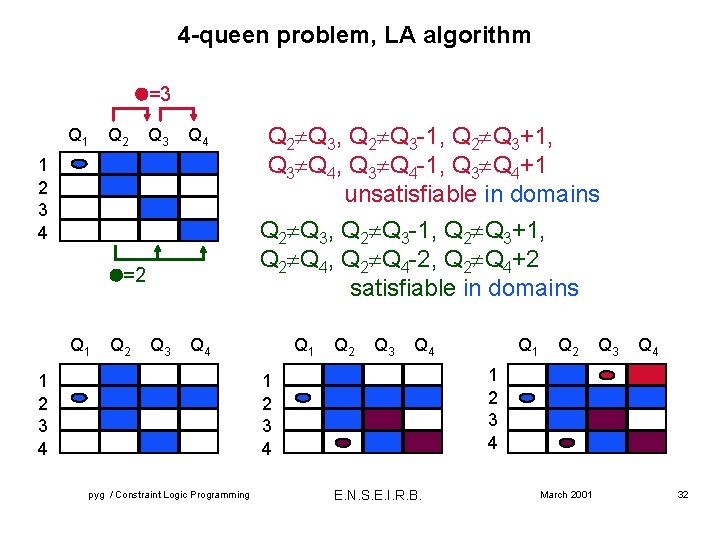
4 -queen problem, LA algorithm =3 Q 1 Q 2 Q 3 Q 4 1 2 3 4 Q 2 Q 3, Q 2 Q 3 -1, Q 2 Q 3+1, Q 2 Q 4 -2, Q 2 Q 4+2 satisfiable in domains =2 Q 1 Q 2 Q 3, Q 2 Q 3 -1, Q 2 Q 3+1, Q 3 Q 4 -1, Q 3 Q 4+1 unsatisfiable in domains Q 3 Q 4 1 2 3 4 Q 1 Q 2 Q 3 Q 4 1 2 3 4 pyg / Constraint Logic Programming Q 1 E. N. S. E. I. R. B. March 2001 32

typical structure of a CLP program CHIP syntax used here % Declare finite domain problem variables: • % [X, Y, Z]: : 1. . 10, Set up the constraints: • % 2*X + 3*Y + 2 #< Z, Search for a solution (labeling): • indomain(X), indomain(Y), indomain(Z). pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 33

CHIP constraint syntax • Linear rational constraints: • • comparators: ^<, ^<=, ^>=, ^= ; operators: +, -, *, / • Finite domain (integer) linear constraints: • • comparators: #<, #<=, #>=, #= ; operators: +, -, *. • Arithmetic (passive) constraints (delayed): • • comparators: <, <=, >, >=, =: =, == ; operators: +, -, *, /. • Regular tree constraints (unification): • comparators: =, =. • Boolean constraints: • • predicates: operators: &=, &=, and/3, nand/3, or/3, nor/3, xor/3, not/2 ; #, ! , 0, 1, symbols. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 34

alldifferent(+List) CHIP constraint • Summary: Holds if all elements of List are different. • +List should be a list of: • non negative integers C ; • finite domain variables X; • terms of the form X+C • alldifferent could have been defined: alldifferent([ ]) alldifferent([E|L]) . : - notmember(E, L), alldifferent(L). notmember(E, [ ]) notmember(E, [F | L]) . : - E #= F, notmember(E, L). pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 35

• element(+Index, +List, -Value) CHIP constraint Summary: Holds if Value is the Indexth element of List: List[Index] = Value • +Index should be: • a non-negative integer; • or a domain variable. • -Value should be: • a free variable; • or a domain variable; • or a non-negative integer. an implementation of “arrays” CHIP also maintains close interaction between Index and Value domains pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 36

labeling variables with CHIP provides great user control over variable labeling: what problem variable should be instantiated first? in what order should a problem variable be bound to its successive domain values? Builtin CHIP labeling predicates: indomain/1; indomain/2; delete/5; [labeling/4. ] Good labeling is tightly related to efficiency! pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 37

indomain/2(+X, +Method) CHIP predicate • Summary: Instantiates X to a value in its domain using Method method. • +X should be one of: • • a non-negative integer ; a domain variable. • +Method should be one: • • min; max; middle; a positive integer. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 38

delete/5(-Selected, +List, -Rest, +Arg, +Method) • Summary: CHIP predicate Selects an element Selected from a list List depending on the Method strategy, yielding Rest as the remainder of the list. • -Selected, -Rest: • a free variable. • +List should be one of: • a list on non-negative integers and domain (when Arg=0); • a list of compound terms. • variables +Arg: • a positive integer. • +Method should be one of • first_fail; most_constrained; • smallest; largest; max_regret. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 39

labeling example in CHIP first fail strategy label([ ]). label([E|L]) : - delete(V, [E|L], R, 0, first_fail), indomain(V), label(R). pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 40

min_max/2(+Goal, +C) min_max/4(+Goal, +C, +Lower, +Upper) min_max/6(+Goal, +C, +Lower, +Upper, +Percent, +Timeout) • Summary: Find solutions with lower and lower cost. • +Goal: • a CHIP query. • +C: • a domain variable or list of FD linear terms. • +Lower, +Upper: • a range for Cost. • +Percent: • integer: each solution improve by Percent%. • +Timeout: • integer: time in seconds allowed for search. pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 41

min_max examples % Minimize the maximum of a list: … length(L, M), L: : 1. . N, alldifferent(L), … min_max(label(L), … % Minimize the sum of a list: … sum_up(L, 0, Sum), Cost : : 0. . 100000, Cost #= Sum, min_max(label(L), Sum), … pyg / Constraint Logic Programming E. N. S. E. I. R. B. March 2001 42