CONSTRAINT GENERATION INTEGER PROGRAMMING APPROACH TO INFORMATION THEORETIC

CONSTRAINT GENERATION INTEGER PROGRAMMING APPROACH TO INFORMATION THEORETIC SENSOR RESOURCE MANAGEMENT MURI Kickoff Meeting Randolph L. Moses November, 2008 MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 1

Selection structures n n Different problems involve different selection structures One common selection structure allows you to select any K observations from a larger set (“K-element subset selection”) MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 2

Selection structures n Another common selection structure is one involving a number of sets, in which you may select one or more observations from each set MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 3

Submodularity n n n Constraint generation approach builds on earlier work developing computable bounds for greedy information gathering. Greedy generation of constraint sets Computable bound gives guarantee on performance relative to an upper bound on optimal constraint generation. MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 4

Directed search n n n Due to submodularity: A family of tighter upper bounds: ( denotes the observations corresponding to the elements in set ) We utilize this concept by using a collection of candidate subsets and exploration subsets MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 5

Integer programming formulation MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 6

Iterative integer programing formulation MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 7

Comments n n At every iteration, the solution of the integer program for that iteration is an upper bound to the optimal reward. The bound becomes tighter with each iteration. At termination an optimal solution is found. We can also add a small number of constraints to the integer program to find an auxiliary problem that provides a lower bound to the optimal reward, which also becomes tighter with each iteration and converges to the optimum. MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 9

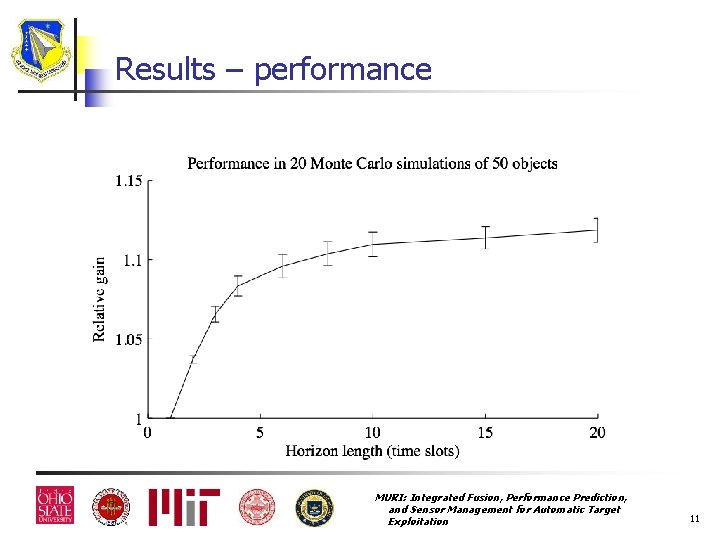
Experiment n n Tracking 50 objects Sensor can provide (for any single object) either Azimuth and range n Azimuth and range rate n n Sensor moves in a race-track pattern, azimuth noise varies with actual azimuth (smallest when object is broadside) Observation noise increases when objects are closely spaced The sensor can also obtain a more accurate azimuth/range or azimuth/range rate observation in 3 time steps MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 10

Results – performance MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 11

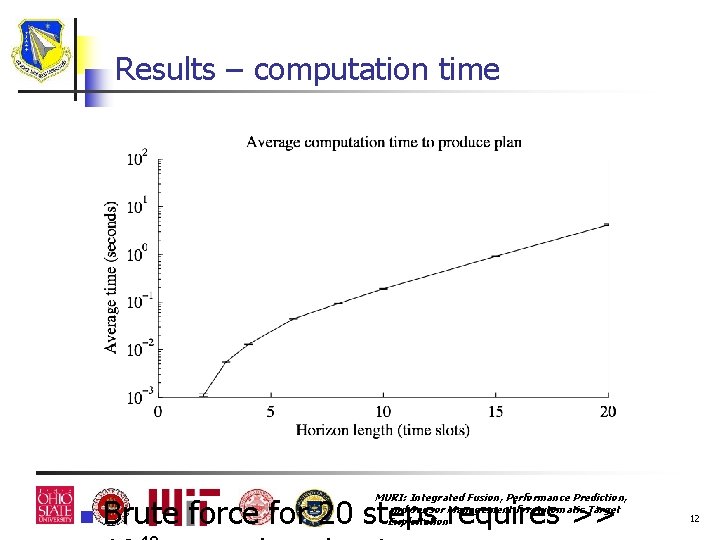
Results – computation time n MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation Brute force for 20 steps requires >> 12

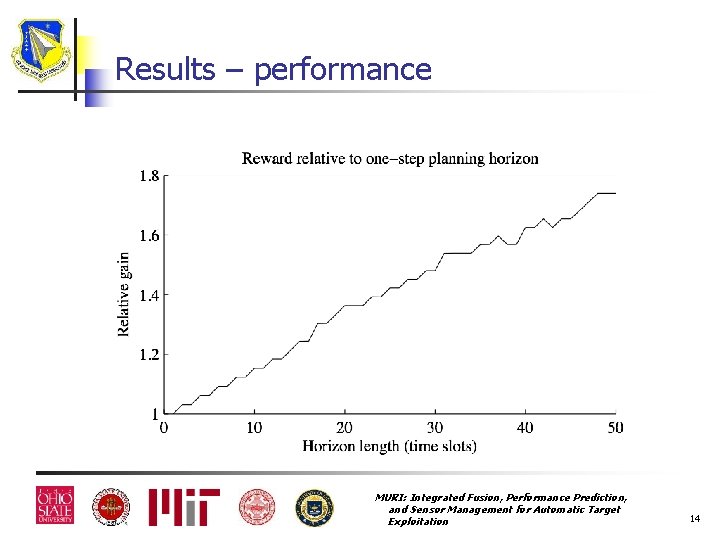
Experiment Tracking 50 objects for 50 time slots n The initial uncertainty of the first 25 objects is slightly lower n Any object can be observed in any time slot n The observation noise for the first 25 objects increases by a factor of 106 halfway through the simulation n MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 13

Results – performance MURI: Integrated Fusion, Performance Prediction, and Sensor Management for Automatic Target Exploitation 14