Constrained Optimization Rong Jin Outline o o Equality

Constrained Optimization Rong Jin

Outline o o Equality constraints Inequality constraints Linear Programming Quadratic Programming

Optimization Under Equality Constraints o o Maximum Entropy Model English ‘in’ French n {dans (1), en (2), à (3), au cours de (4), pendant (5)}

Reducing variables o Representing variables using only p 1 and p 4 o Objective function is changed o Solution: p 1= 0. 2, p 2 = 0. 3, p 3 =0. 1, p 4 = 0. 2, p 5 = 0. 2

Maximum Entropy Model for Classification o o It is unlikely that we can use the previous simple approach to solve such a general Solution: Lagrangian

Equality Constraints: Lagrangian o Introduce a Lagrange multiplier for the equality constraint Construct the Lagrangian o Necessary condition o n A optimal solution for the original optimization problem has to be one of the stationary point of the Lagrangian

Example: o Introduce a Lagrange multiplier for constraint Construct the Lagrangian o Stationary points o

Lagrange Multipliers o o Introducing a Lagrange multiplier for each constraint Construct the Lagrangian for the original optimization problem

Lagrange Multiplier Original Entropy Function Constraints o We have more variables n o p 1, p 2, p 3, p 4, p 5 and, 1, 2, 3 Necessary condition (first order condition) n A local/global optimum point for the original constrained optimization problem a stationary point of the corresponding Lagrangian

Stationary Points for Lagrangian All probabilities p 1, p 2, p 3, p 4, p 5 are expressed as functions of Lagrange multipliers s

Dual Problem o p 1, p 2, p 3, p 4, p 5 are expressed as functions of s o We can even remove the variable 3 o Put together necessary condition o Still difficult to solve

Dual Problem o p 1, p 2, p 3, p 4, p 5 are expressed as functions of s o We can even remove the variable 3 o Put together necessary condition o Still difficult to solve

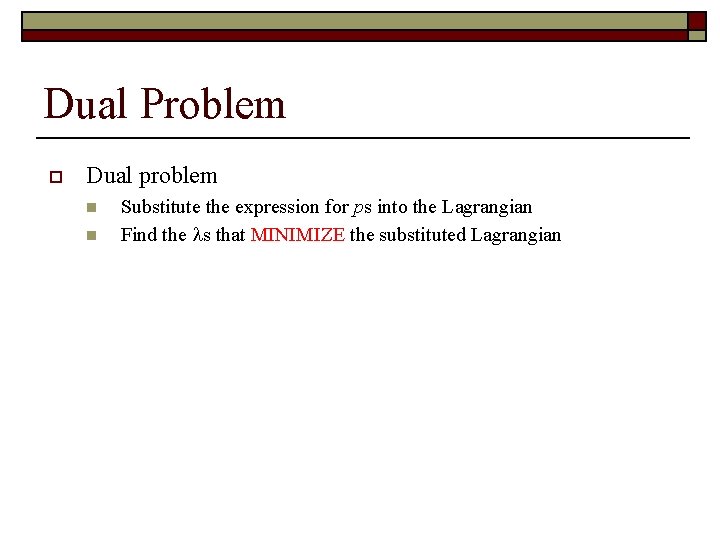
Dual Problem o Dual problem n n Substitute the expression for ps into the Lagrangian Find the s that MINIMIZE the substituted Lagrangian

Dual Problem Original Lagrangian Expression for ps Substituted Lagrangian Finding s such that the above objective function is minimized

Dual Problem o n o o Dual Problem Using dual problem Constrained optimization unconstrained optimization Need to change maximization to minimization Only valid when the original optimization problem is convex/concave (strong duality) Primal Problem x*= * When convex/concave

Maximum Entropy Model for Classification o Introduce a Lagrange multiplier for each linear constraint

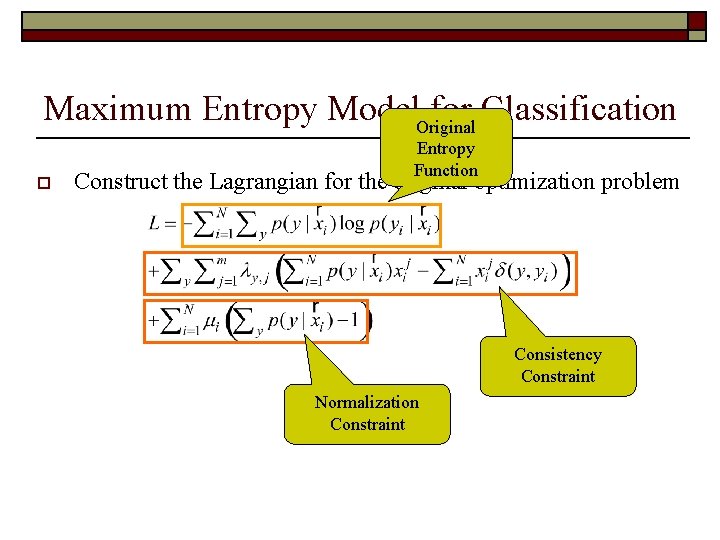
Maximum Entropy Model. Original for Classification o Entropy Function Construct the Lagrangian for the original optimization problem Consistency Constraint Normalization Constraint

Stationary Points Stationary points: first derivatives are zero Conditional Exponential Model ! Sum of conditional probabilities must be one

Dual Problem

Dual Problem

Dual Problem

Dual Problem What is wrong?

Dual Problem

Dual Problem

Dual Problem

Dual Problem

Dual Problem Minimizing L maximizing the log-likelihood

Support Vector Machine o o Having many inequality constraints Solving the above problem directly could be difficult o Many variables: w, b, o Unable to use nonlinear kernel function

Inequality Constraints: Modified Lagrangian o o o Introduce a Lagrange multiplier for the inequality constraint Construct the Lagrangian Two cases: 1. g(x) = c, 2. g(x) > c condition =0 Karush-Kuhn-Tucker (KKT) n A optimal solution for the original optimization problem will satisfy the following conditions Non-negative Lagrange Multiplier

Example: o Introduce a Lagrange multiplier for constraint Construct the Lagrangian o KT conditions o o Expressing objective function using o Solution is =3

Example: o Introduce a Lagrange multiplier for constraint Construct the Lagrangian o KT conditions o o Expressing objective function using o Solution is =3

Example: o Introduce a Lagrange multiplier for constraint Construct the Lagrangian o KKT conditions o o Expressing objective function using o Solution is =3

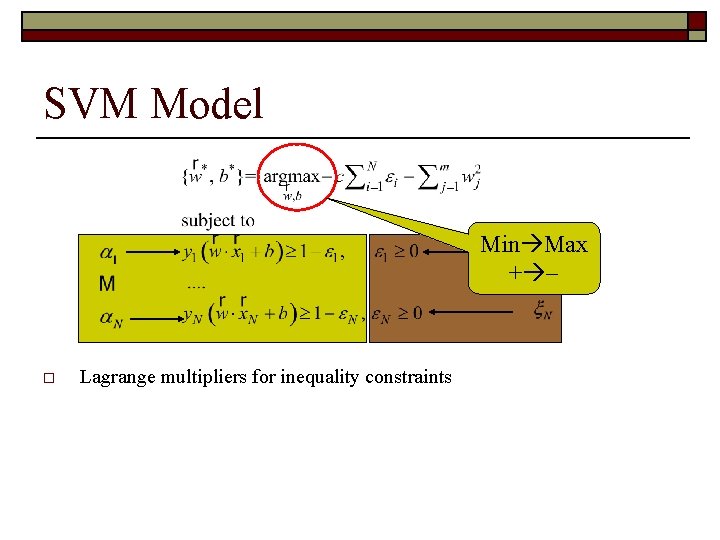
SVM Model Min Max + o Lagrange multipliers for inequality constraints

SVM Model o Lagrangian for SVM model o Karush-Kuhn-Tucker condition

SVM Model o Lagrangian for SVM model o Karush-Kuhn-Tucker condition

Dual Problem for SVM o Express w, b, using and

Dual Problem for SVM o Express w, b, using and o Finding solution satisfying KKT conditions is difficult

Dual Problem for SVM o Rewrite the Lagrangian function using only and o Simplify using KT conditions

Dual Problem for SVM o Final dual problem Maximize Minimize

Quadratic Programming Find Subject to

Linear Programming • Very very useful algorithm • 1300+ papers Find Subject to • 100+ books • 10+ courses • 100 s of companies • Main methods • Simplex method Most important: how to convert a general • Interior point method problem into the above standard form

Example Find Subject to o Need to change max to min

Example Find Subject to o Need change to

Example Find Subject to o Need to convert the inequality

Example Find Subject to o Need change |x 3|