Constitutive Equations CASA Seminar Wednesday 19 April 2006

Constitutive Equations CASA Seminar Wednesday 19 April 2006 Godwin Kakuba

Outline • Introduction – – Continuum mechanics Stress Motions and deformations Conservation laws – – Linear elasticity Viscous fluids Linear viscoelasticity Placticity • Constitutive Equations • Summary

Introduction • Continuum mechanics Matter Molecules Atoms Macroscopic scale

Introduction • Kinematics • Stress • Motions and deformations • Conservation laws

Constitutive Equations Continuum mechanics Eqns that apply equally to all materials • Constitutive equations • Linear elasticity • Viscous fluids • Viscoelasticity • Plasticity Eqns that describe the mechanical behaviour of particular materials

Constitutive equations: Linear elasticity Uniaxial loading: one dimensional elasticity

Constitutive equations: Linear elasticity Linear elastic solid a quadratic function is equal to the rate at which mechanical work is done by the surface and body forces

Constitutive equations: Denote by Linear elasticity thus (a) states that Consider a change of coordinate system, Then, We can also write has the form

Constitutive equations: Interchanging i and j Thus independent constants Linear elasticity

Constitutive equations: Linear elasticity Also independent elastic constants. Using property and the energy conservation equation: But and so

Constitutive equations: But Hence For an isotropic material Linear elasticity

Constitutive equations: Newtonian viscous fluids Constitutive equations of the form For a fluid at rest, If the fluid is isotropic,

Constitutive equations: Newtonian viscous fluids If the stress is a hydrostatic pressure, For an incompressible viscous fluid, or For an ideal fluid, or

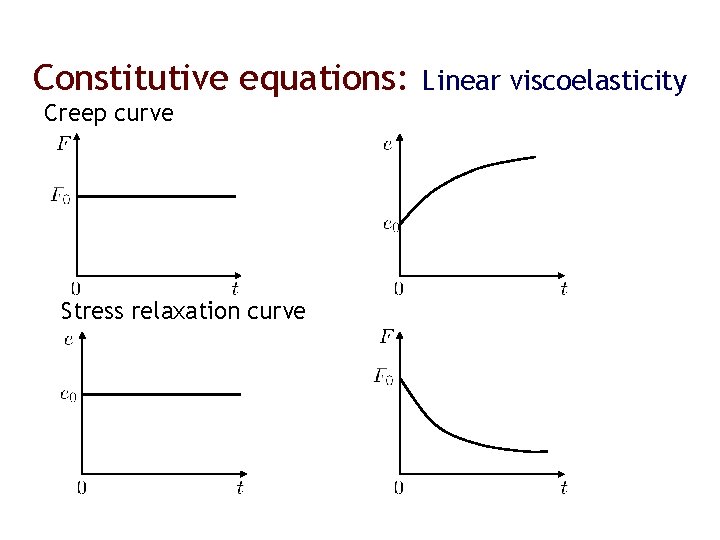
Constitutive equations: Creep curve Stress relaxation curve Linear viscoelasticity

Constitutive equations: Linear viscoelasticity We consider infinitesimal deformations Assuming the superposition principle, then are stress relaxation functions. The inverse relation is are creep functions.

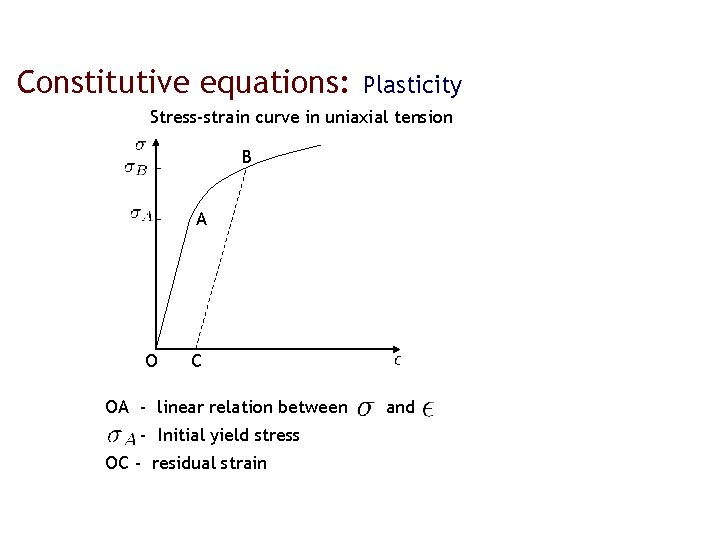
Constitutive equations: Plasticity Stress-strain curve in uniaxial tension B A O C OA - linear relation between - Initial yield stress OC - residual strain and

Constitutive equations: Plasticity For three-dimensional theory of plasticity a yield condition stress-strain relations for elastic behaviour or Thus

Constitutive equations: Plastic stress-strain relations where Hence Plasticity

Constitutive equations: Linear elastic solid: Isotropic material: Newtonian fluid: Viscoelasticity: Plasticity: Summary