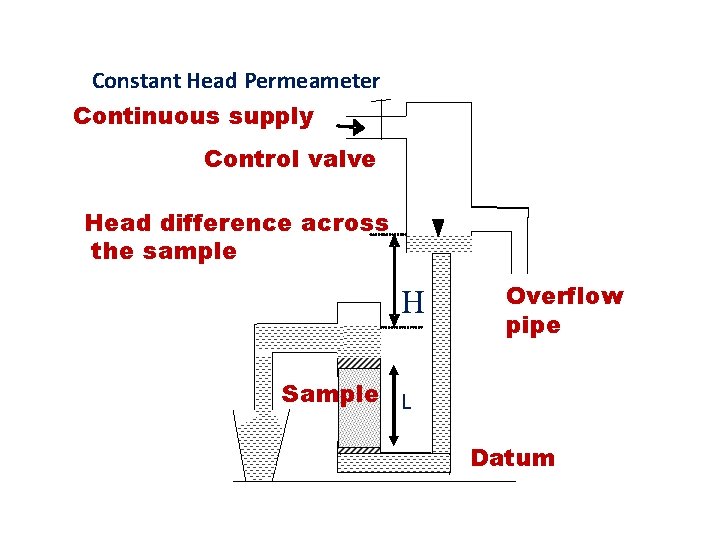
Constant Head Permeameter Continuous supply Control valve Head




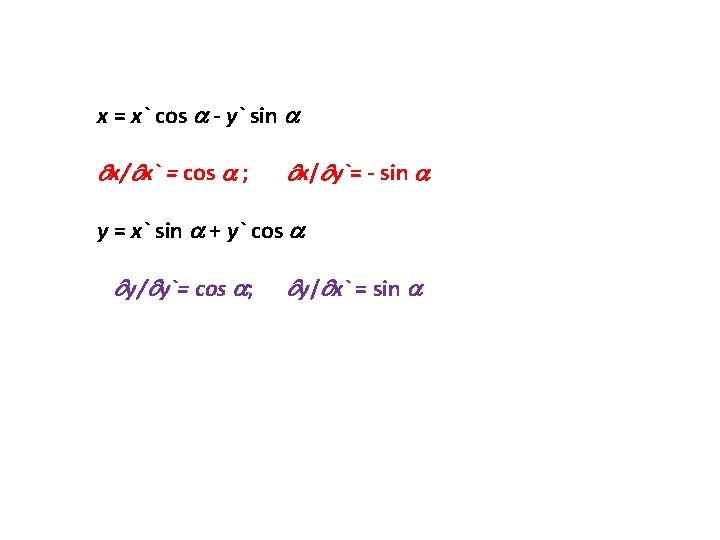



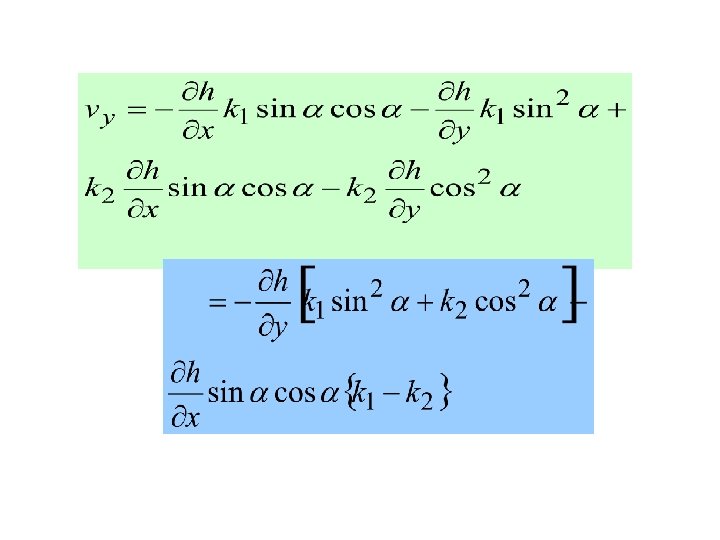
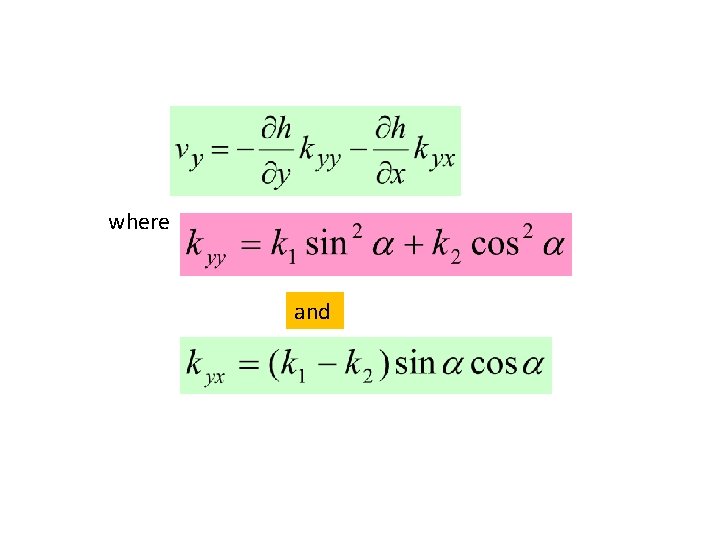

- Slides: 17

Constant Head Permeameter Continuous supply Control valve Head difference across the sample H Overflow pipe Sample L Datum

A constant head permeameter is best suited to find the hydraulic conductivity of samples where k >0. 15 m/d. Q = k. AH/L where H is the constant head difference across the sample of length L and cross sectional area A. If V is the volume of water collected in the storage vessel in time t, then Q = V/ t

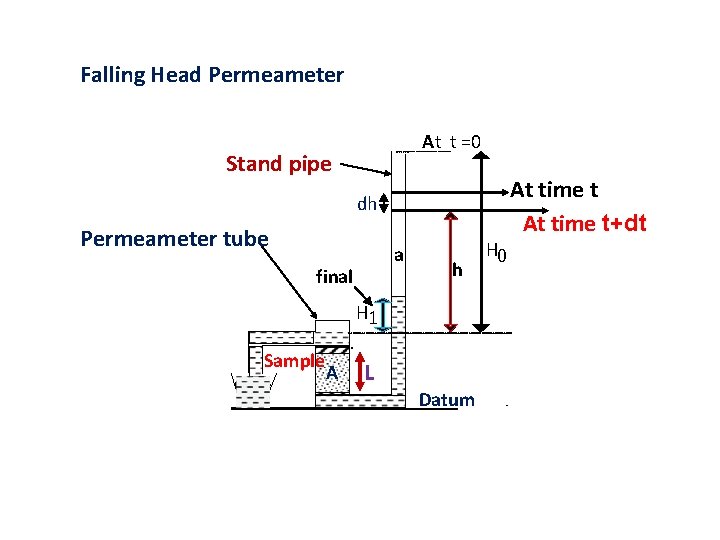
Falling Head Permeameter At t =0 Stand pipe dh Permeameter tube a final h H 1 Sample A L Datum H 0 At time t+dt

Q = -π r 2 dh/dt (negative sign as time is increasing, head difference is decreasing). = k Ah/L, assuming head difference h. Integrating the above expression A mark is given on the stand pipe. If two marks take equal time, then experiment is running well.

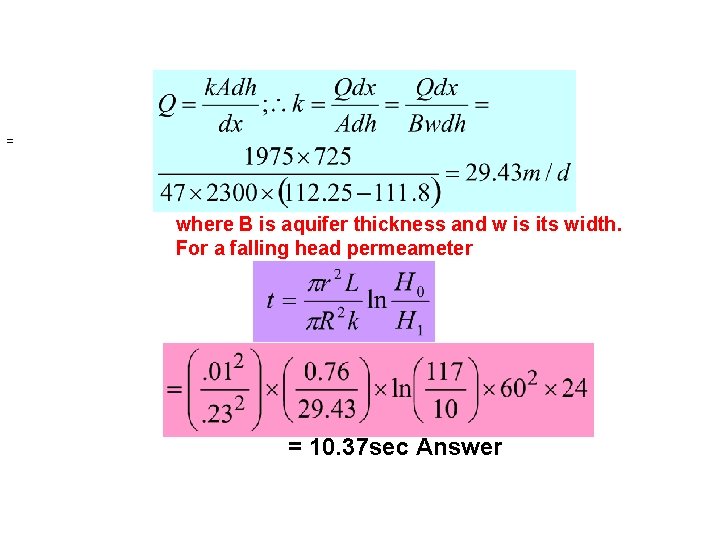
Nu. Prob. 4: Two piezometers 725 m apart measure a groundwater head of 112. 25 m and 111. 8 m respectively in a confined aquifer where the flow rate is 1975 m 3/d. The thickness of the aquifer is 47 m and its width is 2. 3 kms. A 76 cm long sample from this aquifer is placed in a falling head permeameter having the initial water level difference across the sample at 117 cms. The diameters of the permeameter and the standpipe are 23 cm and 1 cm, respectively. Compute the time in seconds when the water level difference in the stand pipe will be 10 cms.

= where B is aquifer thickness and w is its width. For a falling head permeameter = 10. 37 sec Answer

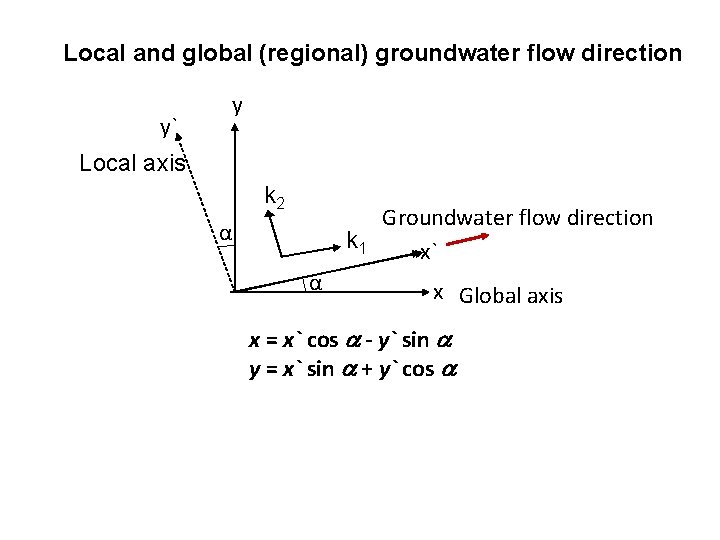
Darcy Velocity in Anisotropic Media When the flow is not along one of the principal axes where kxx, kyy and kyx ( = kxy) are given in terms of the known k 1, k 2 and is the angle between local and global axis. k 1, k 2 are hyd. cond. along two perpendicular directions which do not coincide the principal Cartesian axes.

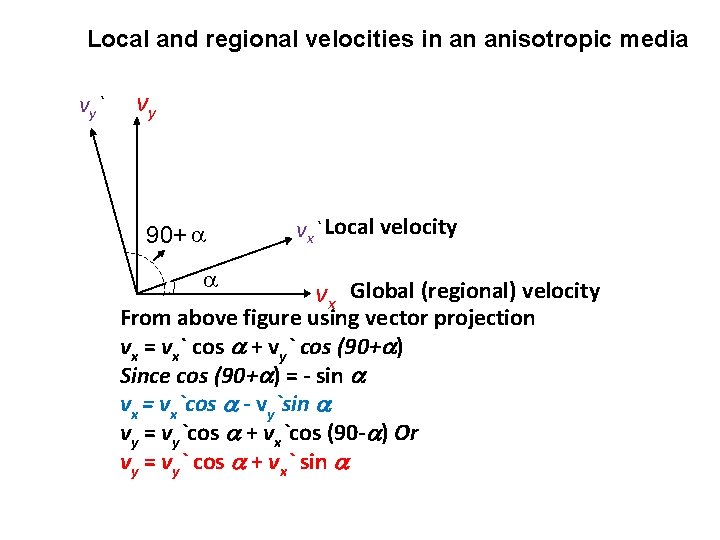
Local and global (regional) groundwater flow direction y` y Local axis k 2 α k 1 α Groundwater flow direction x` x Global axis x = x` cos - y` sin y = x` sin + y` cos

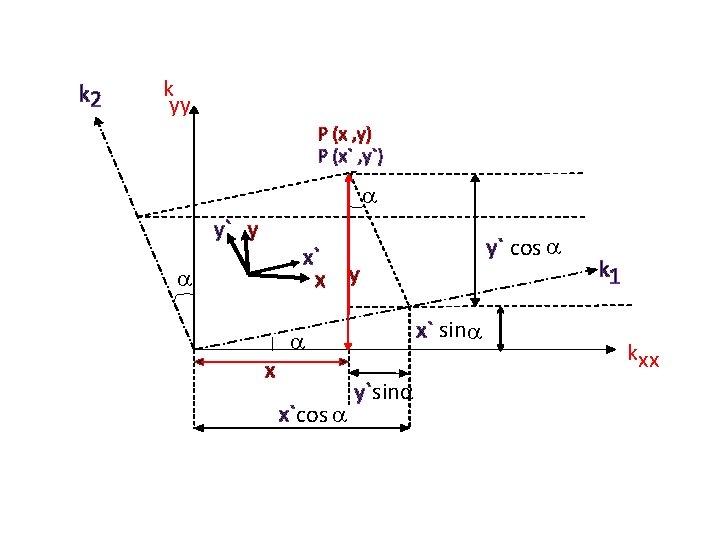
k 2 k yy P (x , y) P (x` , y`) a y` y y` cos a x` x y a x` sina a x x`cos a y`sinα k 1 kxx

Local and regional velocities in an anisotropic media v y` vy 90+ a a vx` Local velocity vx Global (regional) velocity From above figure using vector projection vx = vx` cos + vy` cos (90+ ) Since cos (90+ ) = - sin vx = vx`cos - vy`sin vy = vy`cos + vx`cos (90 - ) Or vy = vy` cos + vx` sin
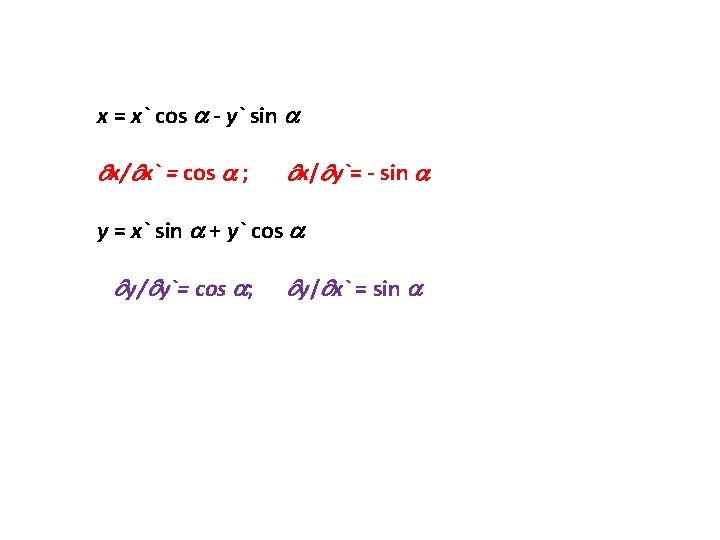
x = x` cos - y` sin x/ x` = cos ; x/ y`= - sin y = x` sin + y` cos y/ y`= cos ; y/ x` = sin

where vx and vy are the Darcy velocities with respect to global co-ordinates and vx` and vy` are the Darcy velocities with respect to local co-ordinates. Also vx`= - k 1 h/ x` and vy` = - k 2 h/ y`, The groundwater head h is a function of x, y, x`, y`. Hence from the chain rule of differentiation,

vx = vx`cos - vy`sin vy = vy` cos + vx` sin Substituting the values of h/ x` and h/ y`

where and Similarly
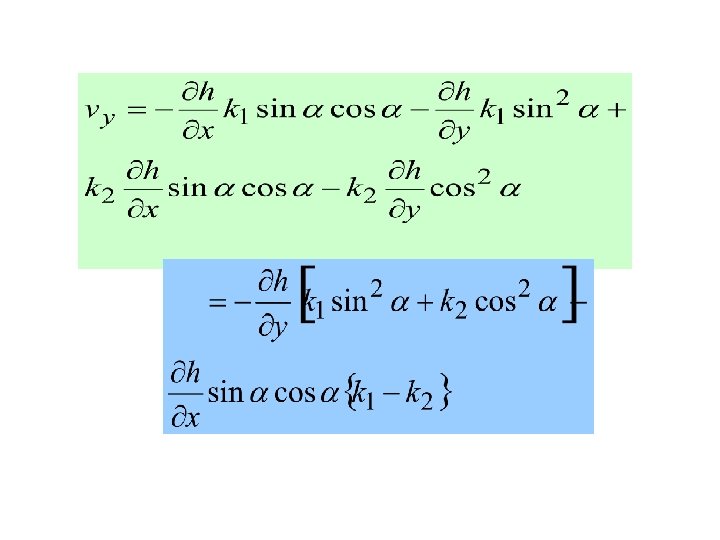
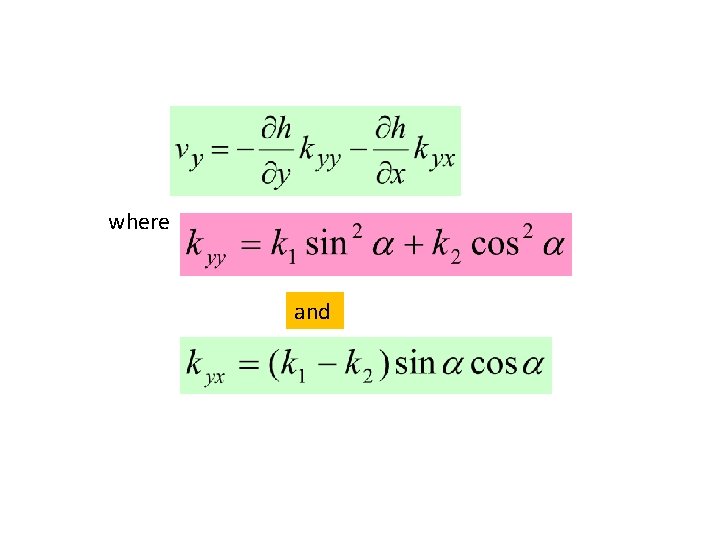
where and

Nu. Prob. : Using Darcy’s law, find h 1 and h 2 for the aquifer conditions shown in Fig. below. Work out the flow across the aquifer. 72 m Ground surface Sticky Clay (Impervious) h 1 k 1=10 20 m k 2=25 20 m k 3=55 m/d 20 m 2. 1 km 65 m h 2 15 m k 6=5 m/d 25 m k 4=100 m/d 10 m k 7=20 m/d 35 m k 5=30 m/d Impervious Bed Rock 2. 8 km 20 m k =40 m/d 8 15 m k 9=10 m/d 1. 4 km