Consistency algorithms Chapter 3 SQ 2009 1 Consistency

Consistency algorithms Chapter 3 SQ 2009 1

Consistency methods l Approximation of inference: l Methods that transform the original network into a tighter and tighter representations • Arc, path and i-consistecy SQ 2009 2

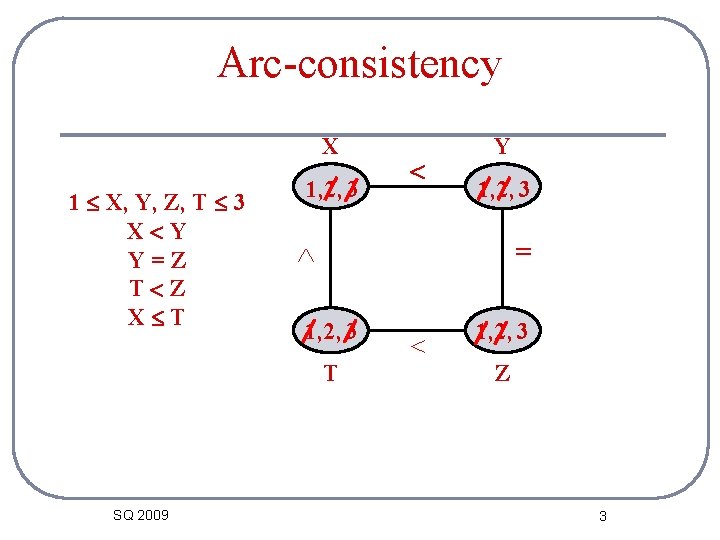
Arc-consistency X 1 X, Y, Z, T 3 X Y Y=Z T Z X T 1, 2, 3 = 1, 2, 3 T SQ 2009 Y 1, 2, 3 Z 3

Arc-consistency X 1 X, Y, Z, T 3 X Y Y=Z T Z X T 1 3 = 2 T SQ 2009 Y 3 Z 4

Arc-consistency SQ 2009 5

Revise for arc-consistency SQ 2009 7

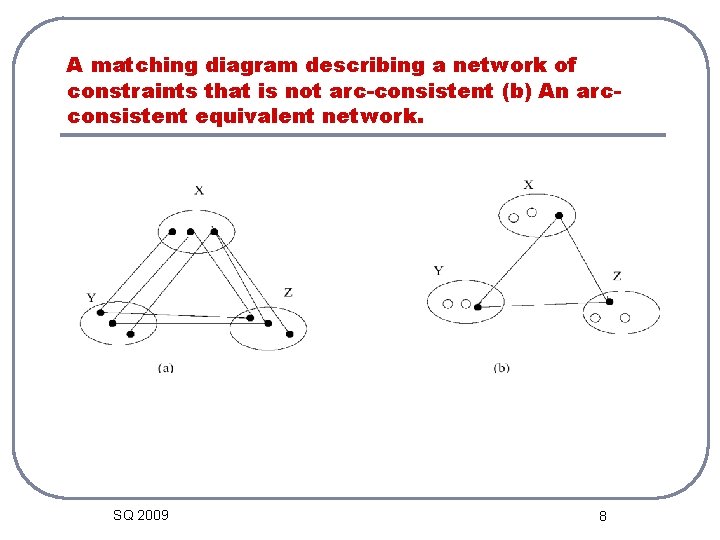
A matching diagram describing a network of constraints that is not arc-consistent (b) An arcconsistent equivalent network. SQ 2009 8

AC-1 l Complexity (Mackworth and Freuder, 1986): e = number of arcs, n variables, k values l (ek^2, each loop, nk number of loops), best-case = ek, l Arc-consistency is: l SQ 2009 9

AC-3 l l Complexity: Best case O(ek), since each arc may be processed in O(2 k) SQ 2009 10

Example: A 3 variables network with 2 constraints: z divides x and z divides y (a) before and (b) after AC-3 is applied. SQ 2009 11

AC-4 l Complexity: l (Counter is the number of supports to ai in xi from xj. S_(xi, ai) is the set of pairs that (xi, ai) supports) SQ 2009 12

Example applying AC-4 SQ 2009 13

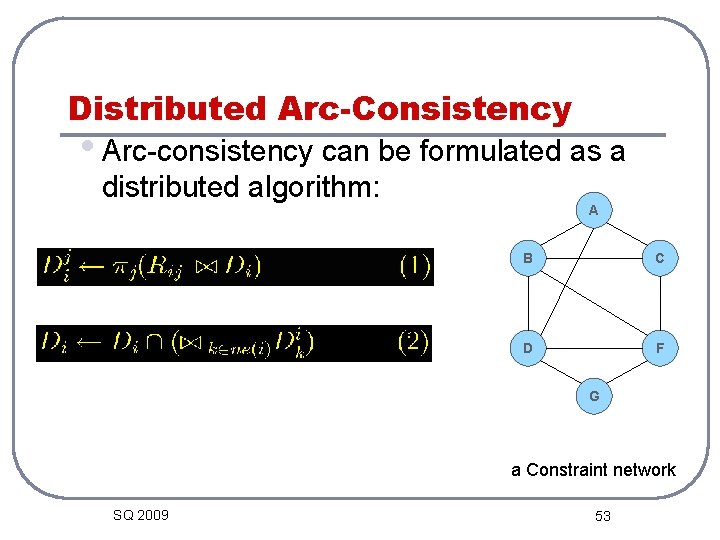
Distributed arc-consistency (Constraint propagation) l Implement AC-1 distributedly. l Node x_j sends the message to node x_i l Node x_i updates its domain: l Messages can be sent asynchronously or scheduled in a topological order SQ 2009 14

Exercise: make the following network arc-consistent l l Draw the network’s primal and dual constraint graph Network = • Domains {1, 2, 3, 4} • Constraints: y < x, z < y, t < z, f<t, x<=t+1, Y<f+2 SQ 2009 15

Arc-consistency Algorithms l l l AC-1: brute-force, distributed AC-3, queue-based AC-4, context-based, optimal AC-5, 6, 7, …. Good in special cases Important: applied at every node of search l (n number of variables, e=#constraints, k=domain size) l Mackworth and Freuder (1977, 1983), Mohr and Anderson, (1985)… SQ 2009 16

Using constraint tightness in analysis t = number of tuples bounding a constraint l l l AC-1: brute-force, AC-3, queue-based AC-4, context-based, optimal AC-5, 6, 7, …. Good in special cases Important: applied at every node of search l (n number of variables, e=#constraints, k=domain size) l Mackworth and Freuder (1977, 1983), Mohr and Anderson, (1985)… SQ 2009 17

Constraint checking Arc-consistency B A B<C [ 1. . 10 ] 2 - A: [ 2. . 10 ] C: [ 6. . 14 ] 6 18 3 - B: [ 5. . 13 ] 14 [ 4. . 15] Overview 1 C: [ 6. . 15 ] [ 5. . 18] 2 2<C-A<5 1 - B: [ 5. . 14 ] 13 14 A<B C

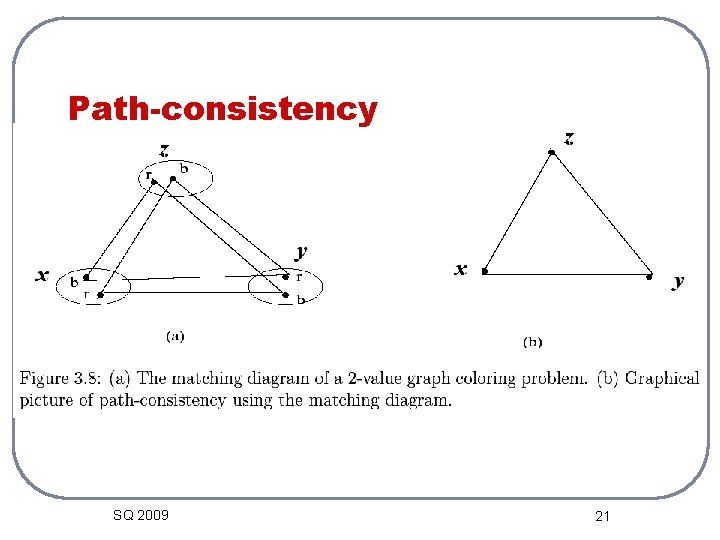
Is arc-consistency enough? l Example: a triangle graph-coloring with 2 values. • • l Is it arc-consistent? Is it consistent? It is not path, or 3 -consistent. SQ 2009 19

Path-consistency SQ 2009 20

Path-consistency SQ 2009 21

Revise-3 l l l Complexity: O(k^3) Best-case: O(t) Worst-case O(tk) SQ 2009 22

PC-1 l Complexity: l O(n^3) triplets, each take O(k^3) steps O(n^3 k^3) Max number of loops: O(n^2 k^2). l SQ 2009 23

PC-2 l Complexity: Optimal PC-4: l (each pair deleted may add: 2 n-1 triplets, number of pairs: O(n^2 k^2) l size of Q is O(n^3 k^2), processing is O(k^3)) SQ 2009 24

Example: before and after pathconsistency l l PC-1 requires 2 processings of each arc while PC-2 may not Can we do path-consistency distributedly? SQ 2009 25

Path-consistency Algorithms l Apply Revise-3 (O(k^3)) until no change l Path-consistency (3 -consistency) adds binary constraints. PC-1: PC-2: PC-4 optimal: l l l SQ 2009 27

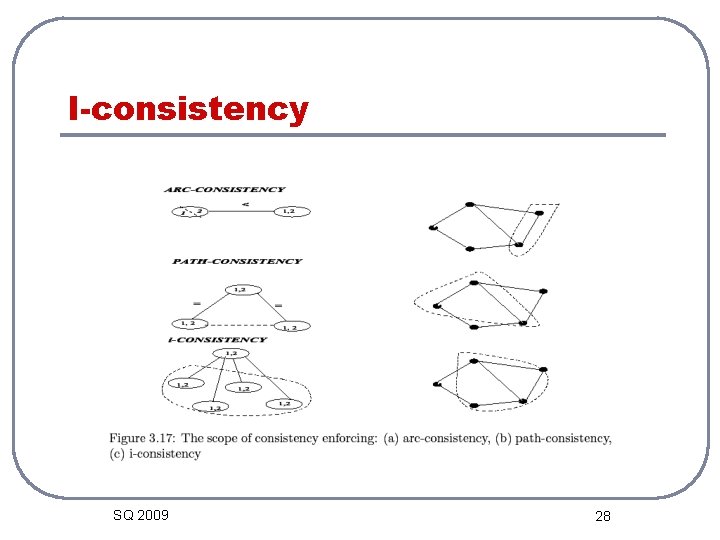
I-consistency SQ 2009 28

Higher levels of consistency, global-consistency SQ 2009 29

Revise-i l l Complexity: for binary constraints For arbitrary constraints: SQ 2009 30

4 -queen example SQ 2009 31

I-consistency SQ 2009 32

Arc-consistency for non-binary constraints: Generalized arc-consistency Complexity: O(t k), t bounds number of tuples. Relational arc-consistency: SQ 2009 34

Examples of generalized arcconsistency x+y+z <= 15 and z >= 13 implies x<=2, y<=2 l l Example of relational arc-consistency SQ 2009 35

More arc-based consistency l Global constraints: e. g. , all-different constraints • Special semantic constraints that appears often in practice and a specialized constraint propagation. Used in constraint programming. l Bounds-consistency: pruning the boundaries of domains SQ 2009 36

Example for alldiff l l l A = {3, 4, 5, 6} B = {3, 4} C= {2, 3, 4, 5} D= {2, 3, 4} E = {3, 4} Alldiff (A, B, C, D, E} Arc-consistency does nothing Apply GAC to sol(A, B, C, D, E)? A = {6}, F = {1}…. Alg: bipartite matching kn^1. 5 (Lopez-Ortiz, et. Al, IJCAI-03 pp 245 (A fast and simple algorithm for bounds consistency of alldifferent constraint) SQ 2009 39

Global constraints l l Alldifferent Sum constraint (variable equal the sum of others) Global cardinality constraint (a value can be assigned a bounded number of times to a set of variables) The cummulative constraint (related to scheduling tasks) SQ 2009 40

Bounds consistency SQ 2009 41

Bounds consistency for Alldifferent constraints SQ 2009 42

Boolean constraint propagation l l (A V ~B) and (B) • B is arc-consistent relative to A but not vice-versa Arc-consistency by resolution: res((A V ~B), B) = A Given also (B V C), path-consistency: Res((A V ~B), (B V C) = (A V C) What will generalized arc-consistency can do to cnfs? Relational arc-consistency rule = unit-resolution SQ 2009 43

Boolean constraint propagation Example: party problem l l l If Alex goes, then Becky goes: If Chris goes, then Alex goes: Query: Is it possible that Chris goes to the party but Becky does not? SQ 2009 44

Gausian and Boolean propagation l Linear inequalities l Boolean constraint propagation SQ 2009 45

Constraint propagation for Boolean constraints: Unit propagation SQ 2009 46

Consistency for numeric constraints SQ 2009 49

Tractable classes SQ 2009 50

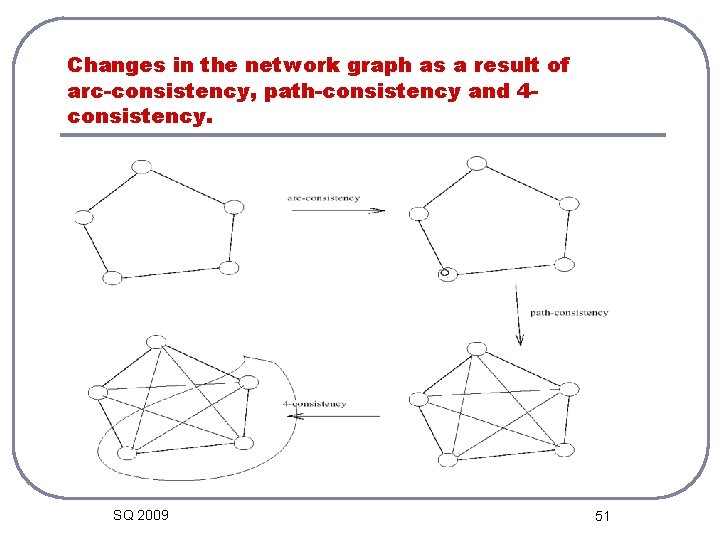
Changes in the network graph as a result of arc-consistency, path-consistency and 4 consistency. SQ 2009 51

Distributed arc-consistency (Constraint propagation) l Implement AC-1 distributedly. l Node x_j sends the message to node x_i l Node x_i updates its domain: l Generalized arc-consistency can be implemented distributedly: sending messages between constraints over the dual graph: SQ 2009 52

Distributed Arc-Consistency • Arc-consistency can be formulated as a distributed algorithm: A B C D F G a Constraint network SQ 2009 53

Relational Arc-consistency The message that R 2 sends to R 1 is A 1 1 2 B 2 3 1 A 2 3 3 1 3 2 R 1 updates its relation and domains and sends messages to neighbors A 1 1 2 2 3 3 SQ 2009 A 1 2 3 B 2 3 1 2 D 3 2 3 1 2 1 B C D F G 1 2 3 2 1 3 54 A C 1 2 3 2 B C F 1 2 3 3 2 1

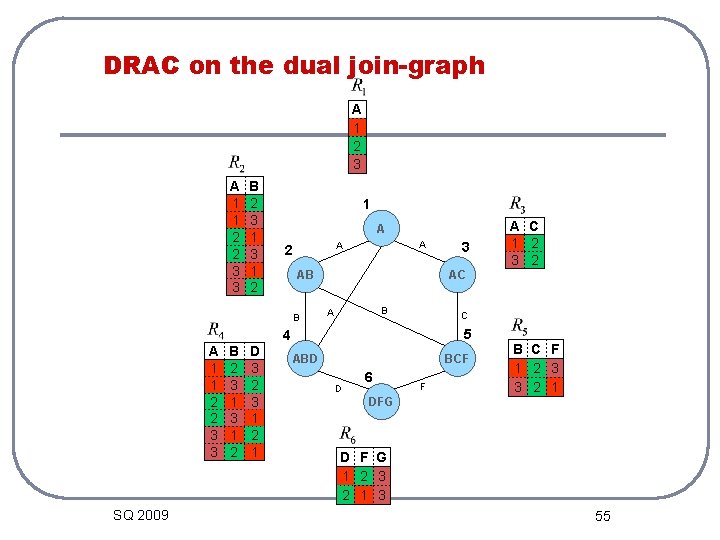
DRAC on the dual join-graph A 1 2 3 A 1 1 2 2 3 3 B 2 3 1 2 1 A A A 2 AB B AC B A C 5 4 A 1 1 2 2 3 3 SQ 2009 B 2 3 1 2 D 3 2 3 1 2 1 3 A C 1 2 3 2 ABD BCF D 6 F B C F 1 2 3 3 2 1 DFG D F G 1 2 3 2 1 3 55

Distributed Relational Arc-Consistency l DRAC can be applied to the dual problem of any constraint network: SQ 2009 56

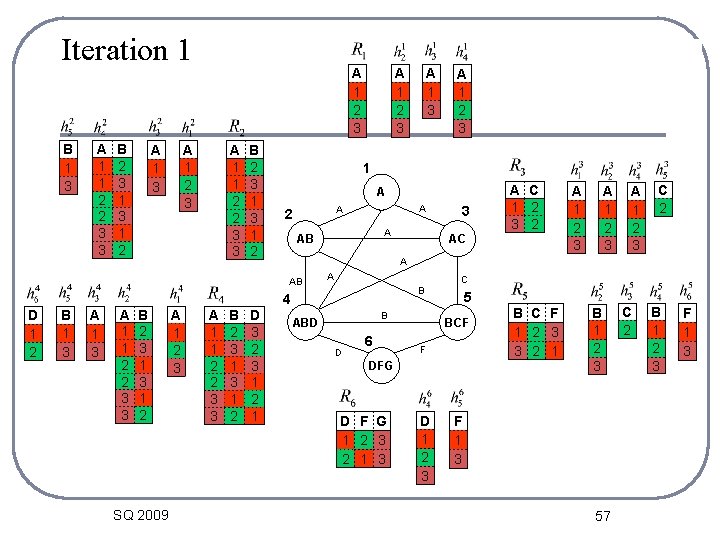
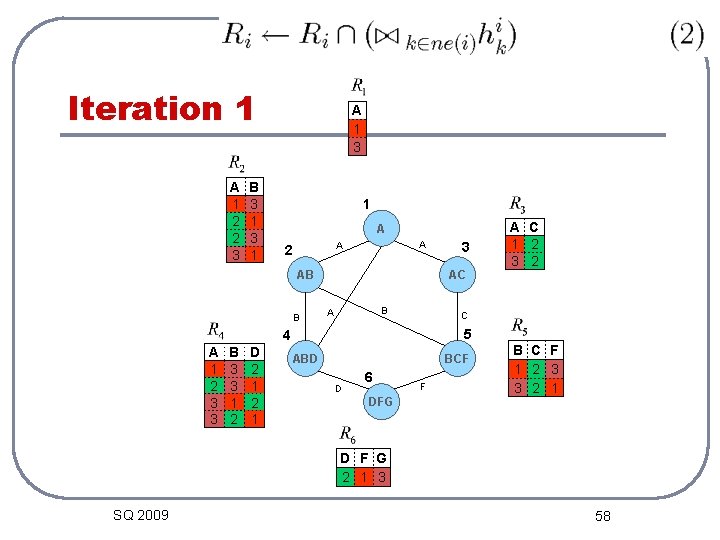
Iteration 1 B 1 3 A 1 1 2 2 3 3 B 2 3 1 2 Node 123456 sends messages A 1 2 3 A 1 1 2 2 3 3 B 2 3 1 2 B 1 3 A 1 1 2 2 3 3 B 2 3 1 2 A SQ 2009 A A 2 A AB A 1 1 2 2 3 3 B 2 3 1 2 D 3 2 3 1 2 1 3 A C 1 2 3 2 AC A 1 2 3 C 2 A A B 4 A 1 2 3 1 AB D 1 2 A 1 3 A 1 2 3 B ABD D 6 C 5 BCF F DFG D F G 1 2 3 2 1 3 D 1 2 3 B C F 1 2 3 3 2 1 B 1 2 3 F 1 3 57 C 2 B 1 2 3 F 1 3

Iteration 1 A 1 2 2 3 B 3 1 A 1 3 1 A A A 2 AB B AC B A C 5 4 A 1 2 3 3 B 3 3 1 2 D 2 1 3 A C 1 2 3 2 ABD BCF D 6 DFG F B C F 1 2 3 3 2 1 D F G 2 1 3 SQ 2009 58

Iteration 2 B 1 3 B 1 2 3 A 1 2 2 3 B 3 1 A 1 3 A 1 2 3 1 A A A 2 AB B 3 AC B A B 1 3 A 1 2 3 3 B 3 3 1 2 D 2 1 5 ABD BCF D 6 F DFG D F G 2 1 3 SQ 2009 C 2 A 1 3 C 4 D 2 A C 1 2 3 2 D 1 2 F 1 3 B C F 1 2 3 3 2 1 B 1 3 59 C 2 F 1

Iteration 2 A 1 3 A B 1 3 3 1 1 A A A 2 AB B AC B A C 5 4 A B D 1 3 2 3 1 2 3 A C 1 2 3 2 ABD BCF D 6 B C F 3 2 1 F DFG D F G 2 1 3 SQ 2009 60

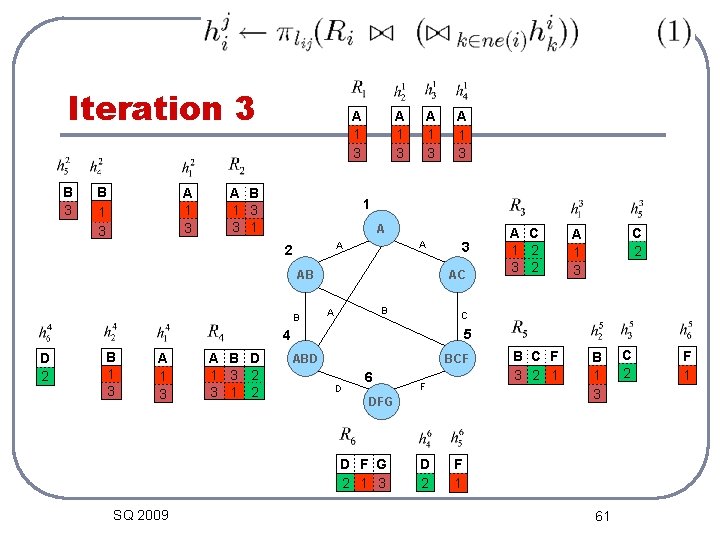
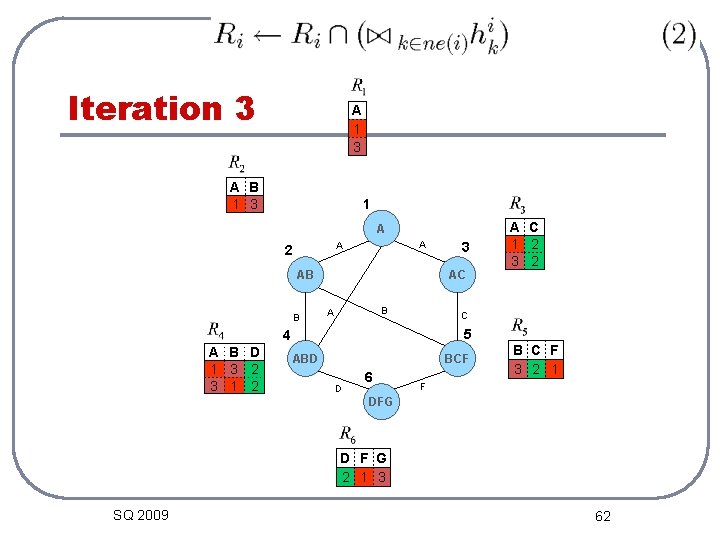
Iteration 3 B 1 3 A B 1 3 3 1 A 1 3 1 A A A 2 AB B 3 AC B A B 1 3 A B D 1 3 2 3 1 2 5 ABD BCF D 6 F DFG D F G 2 1 3 SQ 2009 C 2 A 1 3 C 4 D 2 A C 1 2 3 2 D 2 B C F 3 2 1 B 1 3 F 1 61 C 2 F 1

Iteration 3 A 1 3 A B 1 3 1 A A A 2 AB B AC B A C 5 4 A B D 1 3 2 3 1 2 3 A C 1 2 3 2 ABD BCF D 6 B C F 3 2 1 F DFG D F G 2 1 3 SQ 2009 62

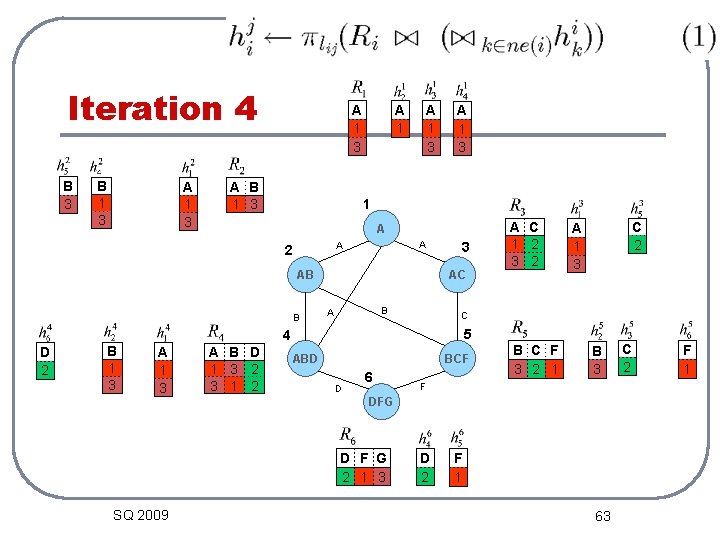
Iteration 4 B 3 B 1 3 A B 1 3 A 1 A 1 3 1 A A A 2 AB B 3 AC B A B 1 3 A B D 1 3 2 3 1 2 5 ABD BCF D 6 B C F 3 2 1 B 3 F DFG D F G 2 1 3 SQ 2009 C 2 A 1 3 C 4 D 2 A C 1 2 3 2 D 2 F 1 63 C 2 F 1

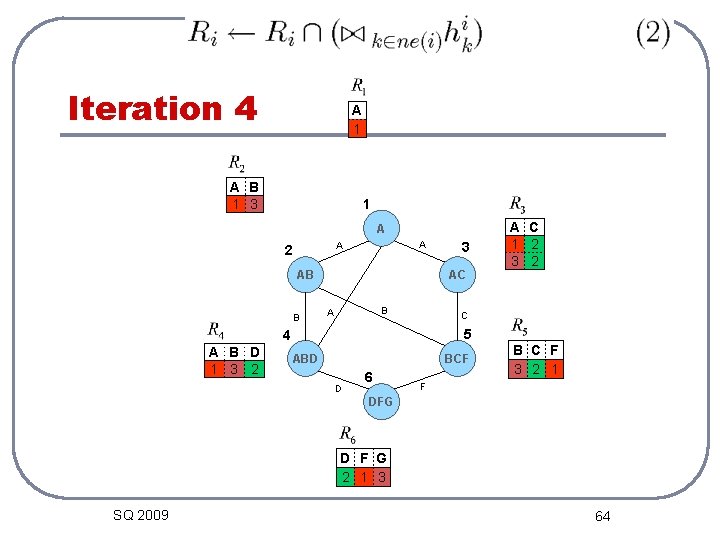
Iteration 4 A 1 A B 1 3 1 A A A 2 AB B AC B A C 5 4 A B D 1 3 2 3 A C 1 2 3 2 ABD BCF D 6 B C F 3 2 1 F DFG D F G 2 1 3 SQ 2009 64

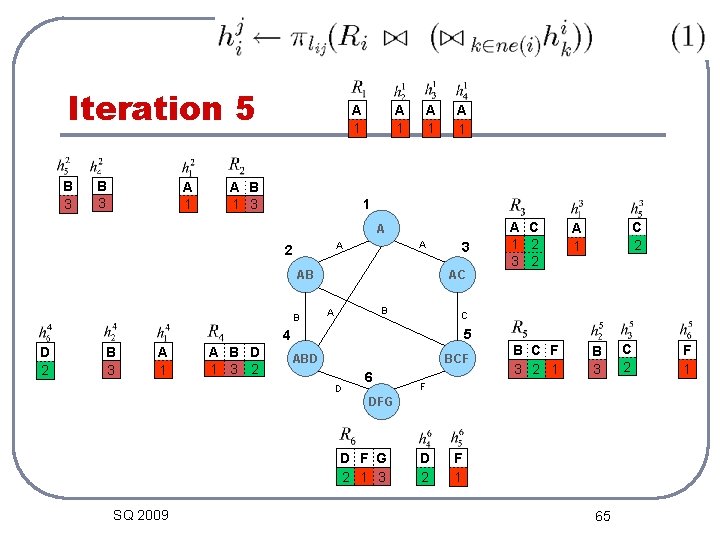
Iteration 5 B 3 A 1 A B 1 3 A 1 A 1 1 A A A 2 AB B 3 AC B A B 3 A 1 A B D 1 3 2 C 2 A 1 C 5 4 D 2 A C 1 2 3 2 ABD BCF D 6 B C F 3 2 1 B 3 F DFG D F G 2 1 3 SQ 2009 D 2 F 1 65 C 2 F 1

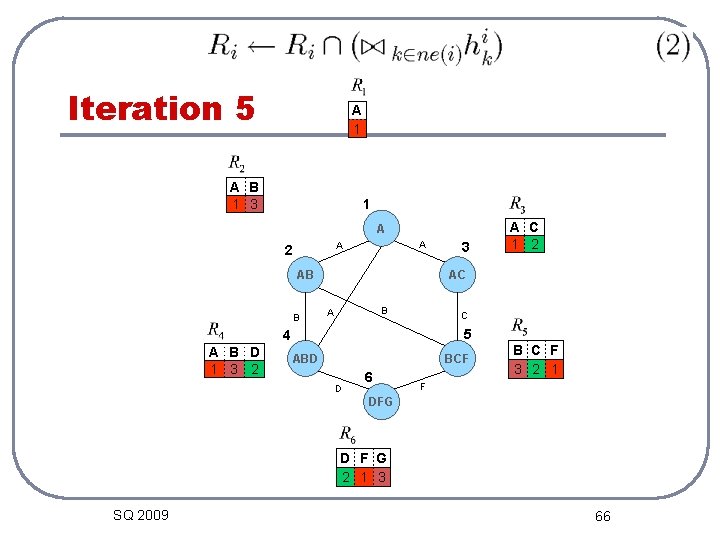
Iteration 5 A 1 A B 1 3 1 A A A 2 AB B AC B A C 5 4 A B D 1 3 2 3 A C 1 2 ABD BCF D 6 B C F 3 2 1 F DFG D F G 2 1 3 SQ 2009 66

What is SAT? Given a sentence: • Sentence: conjunction of clauses • Clause: disjunction of literals • Literal: a term or its negation • Term: Boolean variable Question: Find an assignment of truth values to the Boolean variables such the sentence is satisfied. Overview 1 67

CSP is NP-Complete l Verifying that an assignment for all variables is a solution • Provided constraints can be checked in polynomial time l Reduction from 3 SAT to CSP • Many such reductions exist in the literature (perhaps 7 of them) Overview 1 68

Problem reduction Example: CSP into SAT (proves nothing, just an exercise) Notation: variable-value pair = vvp l vvp term • • l l V 1 = {a, b, c, d} yields x 1 = (V 1, a), x 2 = (V 1, b), x 3 = (V 1, c), x 4 = (V 1, d), V 2 = {a, b, c} yields x 5 = (V 2, a), x 6 = (V 2, b), x 7 = (V 2, c). The vvp’s of a variable disjunction of terms • V 1 = {a, b, c, d} yields (Optional) At most one VVP per variable Overview 1 69

CSP into SAT (cont. ) Constraint: 1. 2. Way 1: Each inconsistent tuple one disjunctive clause • For example: how many? Way 2: a) b) Consistent tuple conjunction of terms Each constraint disjunction of these conjunctions transform into conjunctive normal form (CNF) Question: find a truth assignment of the Boolean variables such that the sentence is satisfied Overview 1 70