Considerations on efficient implementation of Anderson acceleration on

Considerations on efficient implementation of Anderson acceleration on parallel architectures ICERM workshop on methods for large-scale nonlinear problems 9/3/2015 J. Loffeld and C. S. Woodward LLNL-PRES-668437 This work was performed under the auspices of the U. S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC 52 -07 NA 27344. Lawrence Livermore National Security, LLC

We want to implement Anderson acceleration efficiently in SUNDIALS § SUite of Nonlinear and DIfferential/ALgebraic Solvers • Kernels implemented on top of abstract vector library in SIMD fashion • Supports serial, thread-parallel, and MPI-parallel vectors • Starting work on accelerators such as GPUs and the Intel Phi § Currently being tested on two large-scale applications • Para. Di. S – Parallel dislocation dynamics • Ardra - Deterministic neutron transport Lawrence Livermore National 2 LLNL-PRES-668437

Quick review of Anderson acceleration § New vectors added to QR using MGS Least-squares problem solved through QR factorization Lawrence Livermore National § Oldest vectors removed using Givens rotations 3 LLNL-PRES-668437

An “efficient” implementation of AA is about minimizing the cost of QR § Only matters if cost of the function evaluation does not dominate § When QR problem is tall and skinny but not too skinny • m>1 • # Unknowns per processor is high enough to exceed cache Machine balances now exceeding 100 flops/double • # of processors is high enough for communication to matter § Two costs: • Communication • Local BLAS Level 1 operations Lawrence Livermore National 4 LLNL-PRES-668437

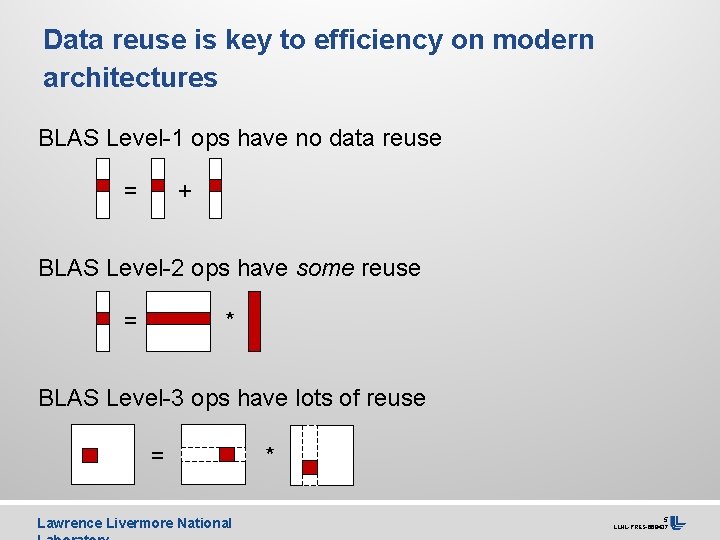
Data reuse is key to efficiency on modern architectures BLAS Level-1 ops have no data reuse = + BLAS Level-2 ops have some reuse = * BLAS Level-3 ops have lots of reuse = Lawrence Livermore National * 5 LLNL-PRES-668437

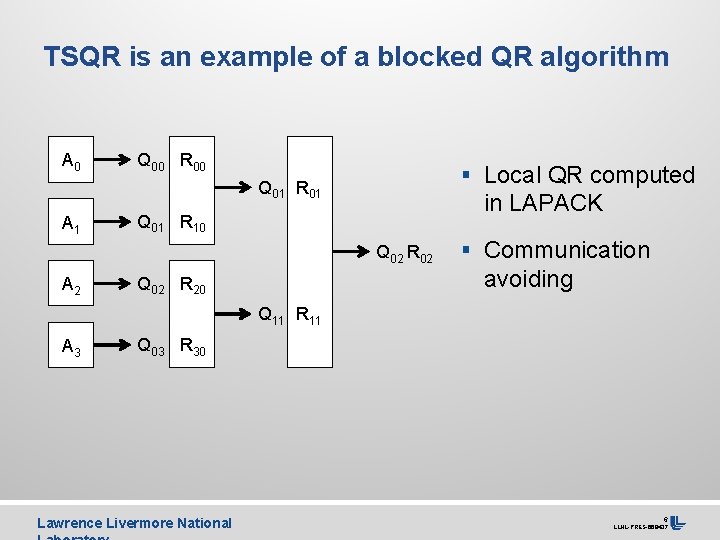
TSQR is an example of a blocked QR algorithm A 0 Q 00 R 00 § Local QR computed Q 01 R 01 A 1 in LAPACK Q 01 R 10 Q 02 R 02 A 2 § Communication avoiding Q 02 R 20 Q 11 R 11 A 3 Q 03 R 30 Lawrence Livermore National 6 LLNL-PRES-668437

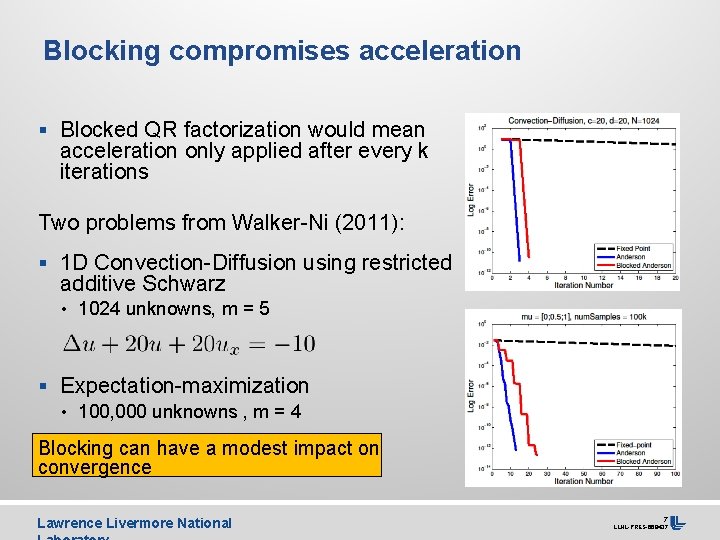
Blocking compromises acceleration § Blocked QR factorization would mean acceleration only applied after every k iterations Two problems from Walker-Ni (2011): § 1 D Convection-Diffusion using restricted additive Schwarz • 1024 unknowns, m = 5 § Expectation-maximization • 100, 000 unknowns , m = 4 Blocking can have a modest impact on convergence Lawrence Livermore National 7 LLNL-PRES-668437

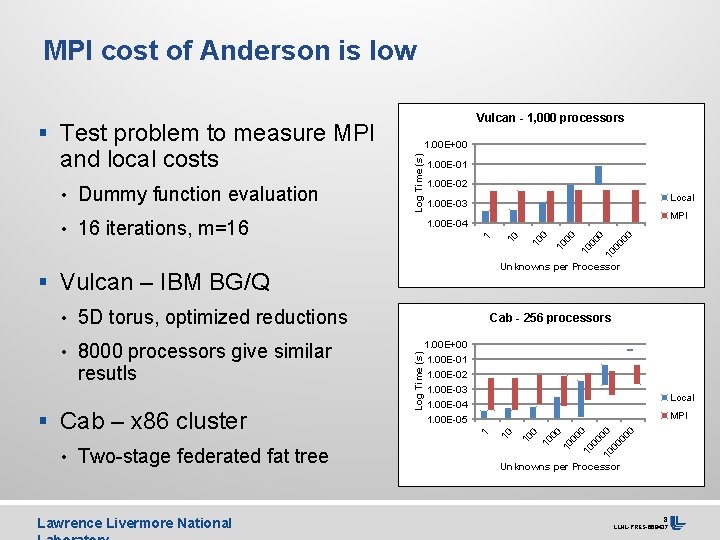
MPI cost of Anderson is low Vulcan - 1, 000 processors § Test problem to measure MPI • 16 iterations, m=16 1. 00 E-01 1. 00 E-02 Local 1. 00 E-03 MPI • 5 D torus, optimized reductions Lawrence Livermore National 10 00 00 00 10 Local MPI 10 00 10 00 0 • Two-stage federated fat tree 1. 00 E+00 1. 00 E-01 1. 00 E-02 1. 00 E-03 1. 00 E-04 1. 00 E-05 1 § Cab – x 86 cluster Cab - 256 processors Log Time (s) resutls 10 0 Unknowns per Processor § Vulcan – IBM BG/Q • 8000 processors give similar 10 1 1. 00 E-04 10 • Dummy function evaluation Log Time (s) and local costs 1. 00 E+00 Unknowns per Processor 8 LLNL-PRES-668437

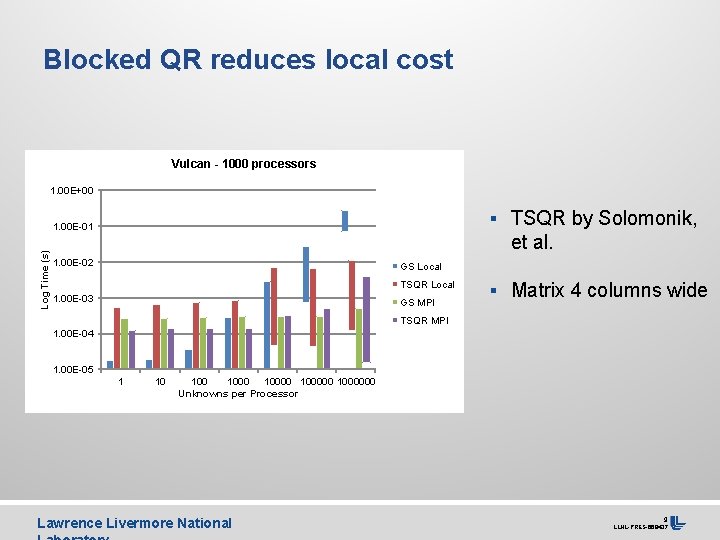
Blocked QR reduces local cost Vulcan - 1000 processors 1. 00 E+00 § TSQR by Solomonik, Log Time (s) 1. 00 E-01 et al. 1. 00 E-02 GS Local TSQR Local 1. 00 E-03 GS MPI § Matrix 4 columns wide TSQR MPI 1. 00 E-04 1. 00 E-05 1 10 100000 1000000 Unknowns per Processor Lawrence Livermore National 9 LLNL-PRES-668437

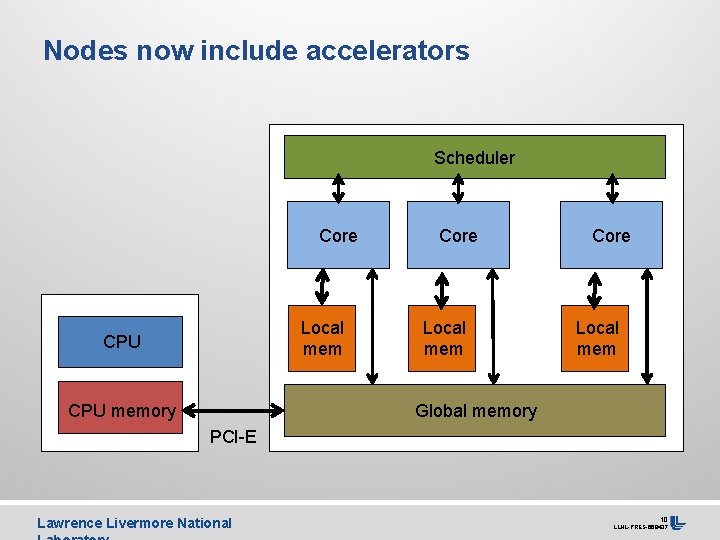
Nodes now include accelerators Scheduler Core Local mem CPU memory Core Local mem Global memory PCI-E Lawrence Livermore National 10 LLNL-PRES-668437

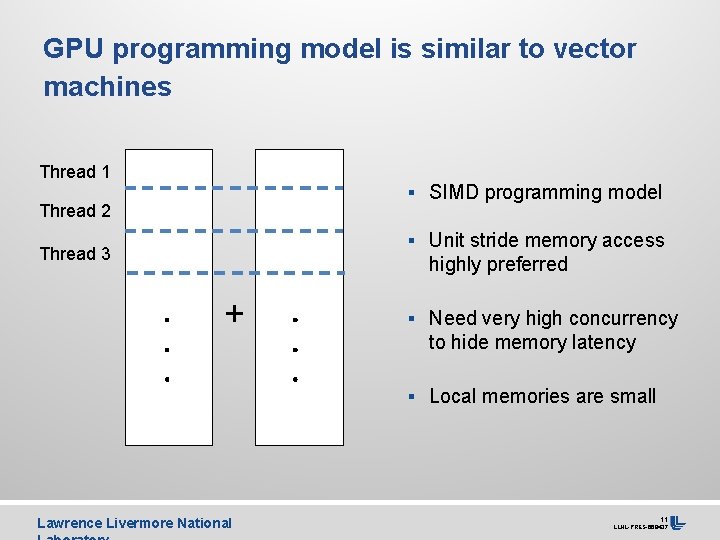
GPU programming model is similar to vector machines Thread 1 § SIMD programming model Thread 2 § Unit stride memory access Thread 3 highly preferred + § Need very high concurrency to hide memory latency § Local memories are small Lawrence Livermore National 11 LLNL-PRES-668437

Initial GPU implementation using Cu. BLAS § Assumes function evaluation on GPU § Maintains approach of Walker (2011) • Modified Gram-Schmidt based QR factorization § Cu. BLAS-based implementation • Main loop on CPU • R matrix on CPU, Q matrix on GPU • 10 µs latency each kernel launch • Expect to be highly bandwidth bound Lawrence Livermore National 12 LLNL-PRES-668437

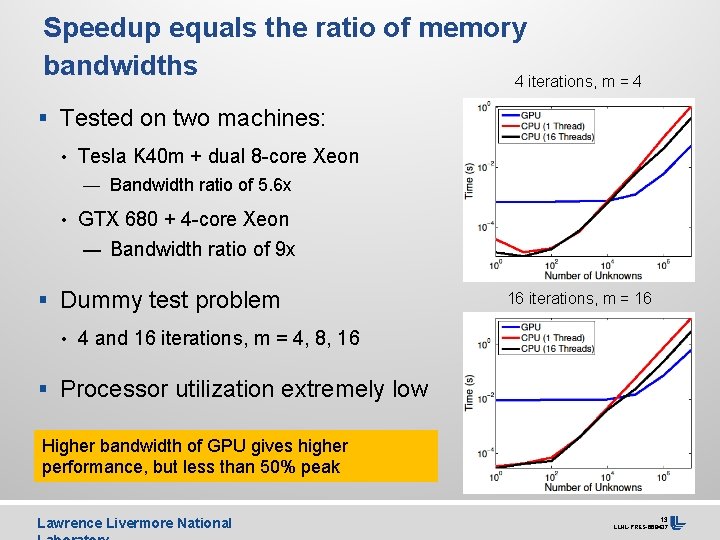
Speedup equals the ratio of memory bandwidths 4 iterations, m = 4 § Tested on two machines: • Tesla K 40 m + dual 8 -core Xeon — Bandwidth ratio of 5. 6 x • GTX 680 + 4 -core Xeon — Bandwidth ratio of 9 x § Dummy test problem 16 iterations, m = 16 • 4 and 16 iterations, m = 4, 8, 16 § Processor utilization extremely low Higher bandwidth of GPU gives higher performance, but less than 50% peak Lawrence Livermore National 13 LLNL-PRES-668437

Classical Gram-Schmidt allows more concurrency and data reuse § Can be implemented with BLAS level-2 operations § Instability countered using reorthogonolization § As long as full rank, only need one reorthogonalization § Various cheap tests to determine if correction needed Lawrence Livermore National 14 LLNL-PRES-668437

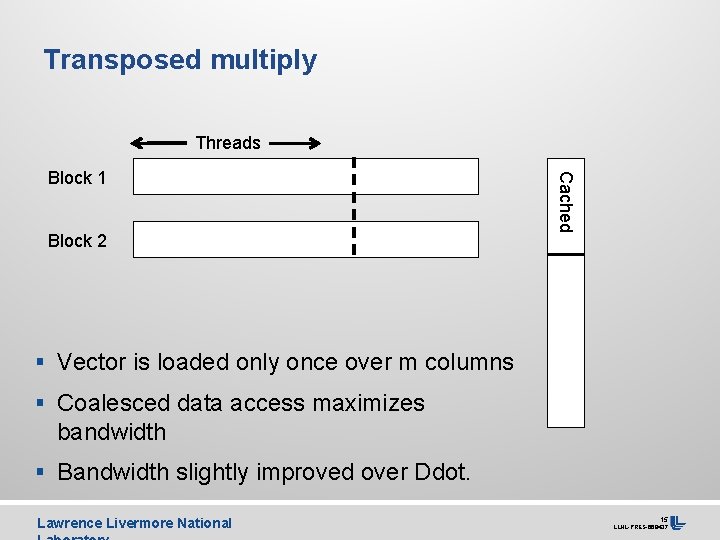
Transposed multiply Threads Block 2 Cached Block 1 § Vector is loaded only once over m columns § Coalesced data access maximizes bandwidth § Bandwidth slightly improved over Ddot. Lawrence Livermore National 15 LLNL-PRES-668437

Conclusions § MPI cost is not a bottleneck for QR implementation of Anderson § On GPUs, kernels completely memory bound • High bandwidth of device means high performance relative to CPU • CGS can minimize redundant loads of vectors • Need to test if reorthogonalization ruins benefit • Kernels still need to be refined § Having Anderson close to function evaluation is likely the real benefit Lawrence Livermore National 16 LLNL-PRES-668437

The QR update is done in-place § New vectors added using modified Gram Schmidt • Implemented using dot products • Communication from MPI_Allreduce § Oldest vector removed from QR through Givens rotations • No MPI communication, but non-trivial local cost Lawrence Livermore National 18 LLNL-PRES-668437

Open questions § How often is reorthogonalization needed? § Maintains approach of Walker (2011) • Modified Gram-Schmidt based QR factorization § Cu. BLAS-based implementation • Main loop on CPU • R matrix on CPU, Q matrix on GPU • 10 µs latency each kernel launch • Expect to be highly bandwidth bound Lawrence Livermore National 19 LLNL-PRES-668437

Restarting not compelling versus “sliding” § 2 D Poisson using RAS • 4 subdomains per direction Time (s) Vulcan - 16 processors • 3 cells overlap 0. 1 0. 09 0. 08 0. 07 0. 06 0. 05 0. 04 0. 03 0. 02 0. 01 0 32 42 33 49 47 71 Sliding Restarting 5 10 m 15 § 16 processors Cab - 16 processors Time (s) § Non-blocked linear algebra 0. 04 0. 035 0. 03 0. 025 0. 02 0. 015 0. 01 0. 005 0 32 33 47 71 42 Sliding Restarting 5 Lawrence Livermore National 49 10 m 15 20 LLNL-PRES-668437